Nội dung từ Loigiaihay.Com
Đường tiệm cận là gì? Cách nhận biết đường tiệm cận đứng, tiệm cận ngang, tiệm cận xiên - Toán 12
1. Tiệm cận đứng là gì?
2. Tiệm cận ngang là gì?
3. Đường tiệm cận xiên là gì?
4. Cách nhận biết đường tiệm cận
5. Bài tập vận dụng
1. Tiệm cận đứng là gì?
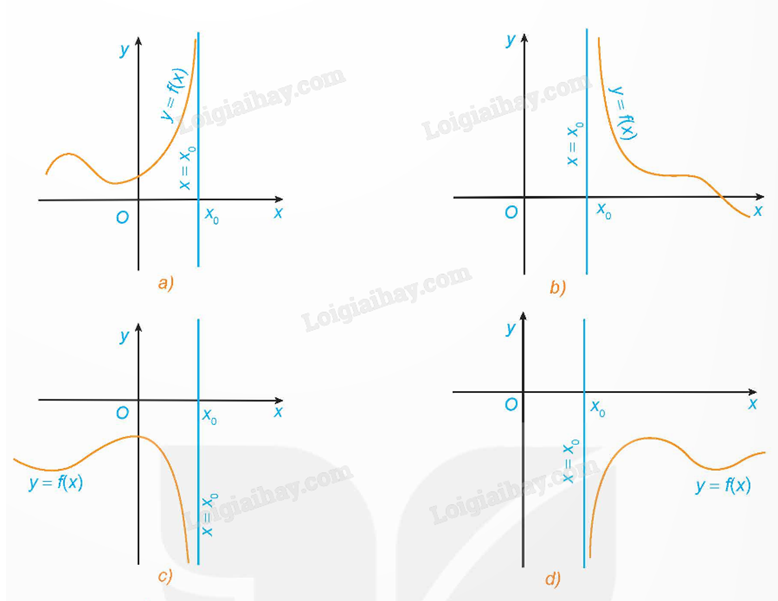
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
2. Tiệm cận ngang là gì?
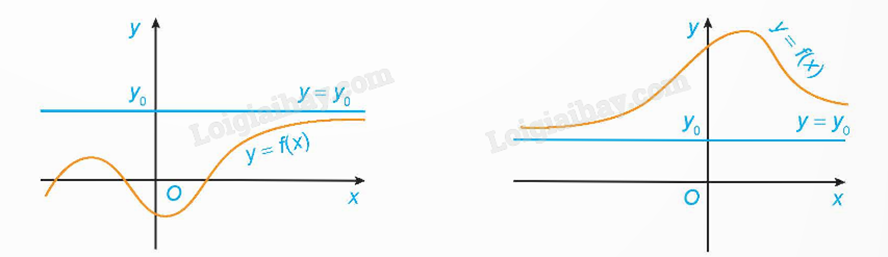
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
3. Đường tiệm cận xiên là gì?
Đường thẳng y = ax + b \((a \ne 0)\) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
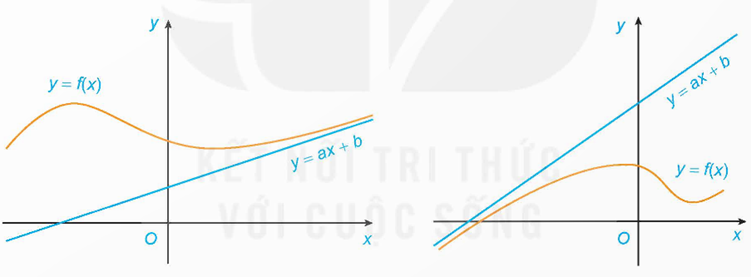
4. Cách nhận biết đường tiệm cận
a)
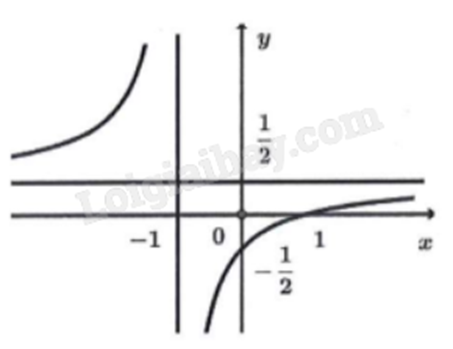
Tiệm cận ngang của đồ thị hàm số trên là \(y = \frac{1}{2}\).
Tiệm cận đứng của đồ thị hàm số trên là \(x = -\frac{1}{2}\).
b)
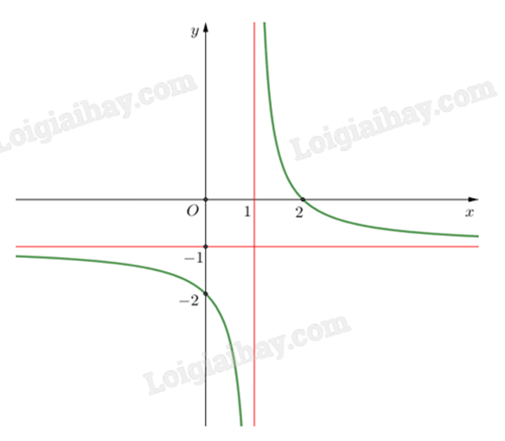
Tiệm cận đứng của đồ thị hàm số trên là x = 1.
Tiệm cận ngang của đồ thị hàm số trên là y = -1.
c)
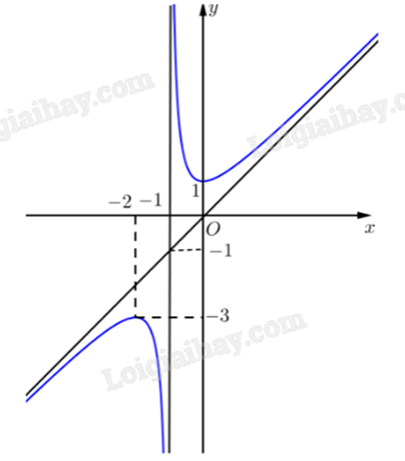
Tiệm cận đứng của đồ thị hàm số trên là x = -1.
Phương trình đường tiệm cận xiên có dạng y = ax + b \((a \ne 0)\).
Đường tiệm cận xiên đi qua hai điểm có toạ độ (0;0) và (-1;-1) nên ta có:
\(\left\{ {\begin{array}{*{20}{l}}{0 = a.0 + b}\\{ - 1 = a.( - 1) + b}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 0}\end{array}} \right. \Rightarrow y = x\)
Vậy phương trình đường tiệm cận xiên là y = x.
5. Bài tập vận dụng
Các bài khác cùng chuyên mục













