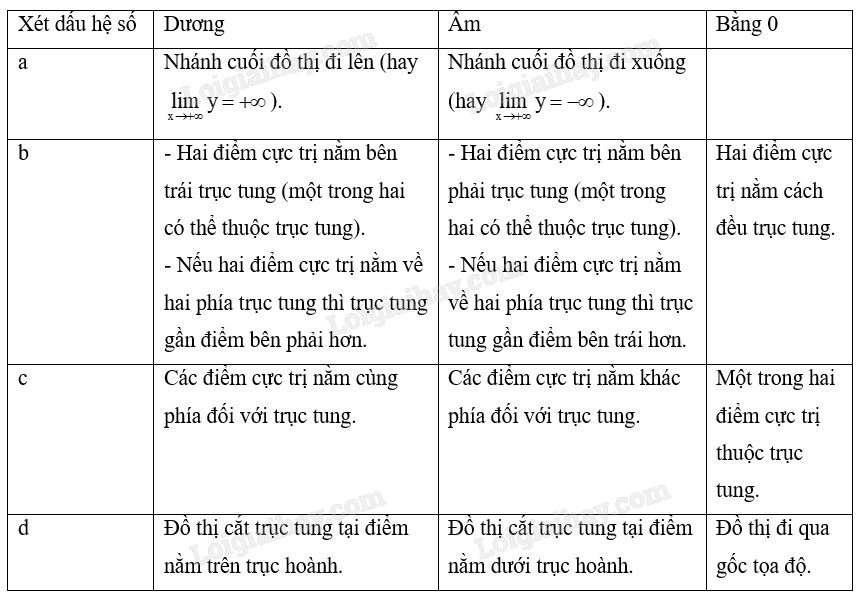
Nội dung từ Loigiaihay.Com
Cách xét dấu hệ số của hàm số biết đồ thị - Toán 12
1. Hệ số là gì?
2. Cách xét dấu hệ số của hàm đa thức bậc ba biết đồ thị
3. Cách xét dấu hệ số của hàm phân thức bậc nhất biết đồ thị
4. Bài tập vận dụng
1. Hệ số là gì?
Trong toán học, hệ số là một số nhân (nhân tử) trong một vài số hạng của một biểu thức. Một giá trị mà nó xuất hiện phía trước hoặc xuất hiện trong phép nhân với một giá trị khác và thường là một số nhưng không phải biến số.
Ví dụ minh hoạ:
7x2+6y+5z−4 thì 7 là hệ số của x2, 6 là hệ số của y, 5 là hệ số của z; 4 là hằng số.
2. Cách xét dấu hệ số của hàm đa thức bậc ba biết đồ thị
Cho đồ thị hàm số y=ax3+bx2+cx+d (a≠0) có hai điểm cực trị.
Ví dụ minh hoạ:
Cho hàm số bậc ba y=ax3+bx2+cx+d có đồ thị dưới đây.
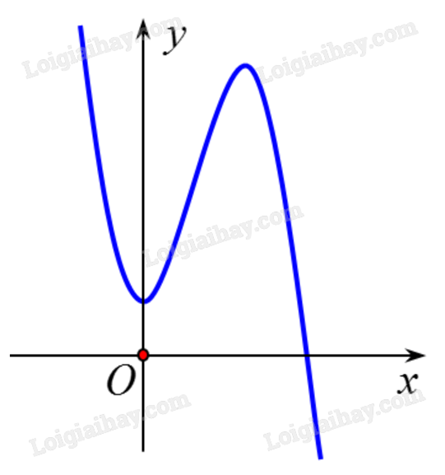
Nhánh cuối đồ thị đi xuống (hay limx→+∞y=−∞) nên a < 0.
Một điểm cực trị nằm bên phải trục tung và một điểm cực trị thuộc trục tung nên b < 0.
Một điểm cực trị thuộc trục tung nên c = 0.
Đồ thị cắt trục tung phía trên trục hoành nên d > 0.
3. Cách xét dấu hệ số của hàm phân thức bậc nhất biết đồ thị
Cho đồ thị hàm số y=ax+bcx+d (c≠0,ad−bc≠0).
Hàm số đồng biến trên tập xác định: ad – bc > 0.
Hàm số nghịch biến trên tập xác định: ad – bc < 0.
Đồ thị hàm số cắt trục Oy tại điểm nằm trên trục hoành: bd > 0.
Đồ thị hàm số cắt trục Oy tại điểm nằm dưới trục hoành: bd < 0.
Đường tiệm cận đứng của đồ thị nằm bên phải trục tung: −dc>0⇔cd<0.
Đường tiệm cận đứng của đồ thị nằm bên trái trục tung: −dc<0⇔cd>0.
Đường tiệm cận ngang của đồ thị nằm phía trên trục hoành: ac>0⇔ac>0.
Đường tiệm cận ngang của đồ thị nằm phía dưới trục hoành: ac<0⇔ac<0.
Ví dụ minh hoạ:
Cho đồ thị hàm số y=ax+bcx+d. Mệnh đề nào đúng?
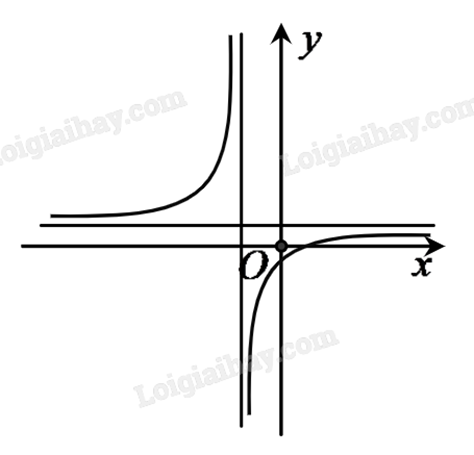
A. {ad<0bc>0
B. {ad<0bc<0
C. {ad>0bc<0
D. {ad>0bc>0
Đường tiệm cận ngang của đồ thị nằm phía trên trục hoành: ac>0⇔ac>0.
Đường tiệm cận đứng của đồ thị nằm bên trái trục tung: −dc<0⇔cd>0.
Đồ thị hàm số cắt trục Oy tại điểm nằm dưới trục hoành: bd < 0.
Ta có {ac>0cd>0⇒ad>0; {cd>0bd<0⇒bc<0. Vậy đáp án đúng là C.
4. Bài tập vận dụng
Các bài khác cùng chuyên mục
- Cách tìm hàm số biết đồ thị hoặc bảng biến thiên - Toán 12
- Cách nhận dạng đồ thị hàm số - Toán 12
- Khái niệm và cách tìm tâm đối xứng của đồ thị hàm số - Toán 12
- Cách nhận dạng đồ thị hàm số chứa dấu giá trị tuyệt đối - Toán 12
- Cách giải bài toán về tốc độ thay đổi của một đại lượng ứng dụng đạo hàm - Toán 12













