Cách nhận dạng đồ thị hàm số - Toán 12

Cho hàm số $y = a{x^3} + b{x^2} + cx + d$ $(a,b,c,d \in \mathbb{R},a \ne 0)$.

Đạo hàm: $y' = 3a{x^2} + 2bx + c$.

Nếu nhánh cuối đồ thị đi lên thì a > 0, nhánh cuối đồ thị đi xuống thì a < 0.

Đồ thị cắt trục tung tại điểm (0;d).

Đồ thị hàm số đi qua điểm $A\left( {{x_A};{y_A}} \right)$ thì $f\left( {{x_A}} \right) = {y_A} \Leftrightarrow a{x_A}^3 + b{x_A}^2 + c{x_A} + {d_A} = {y_A}$.

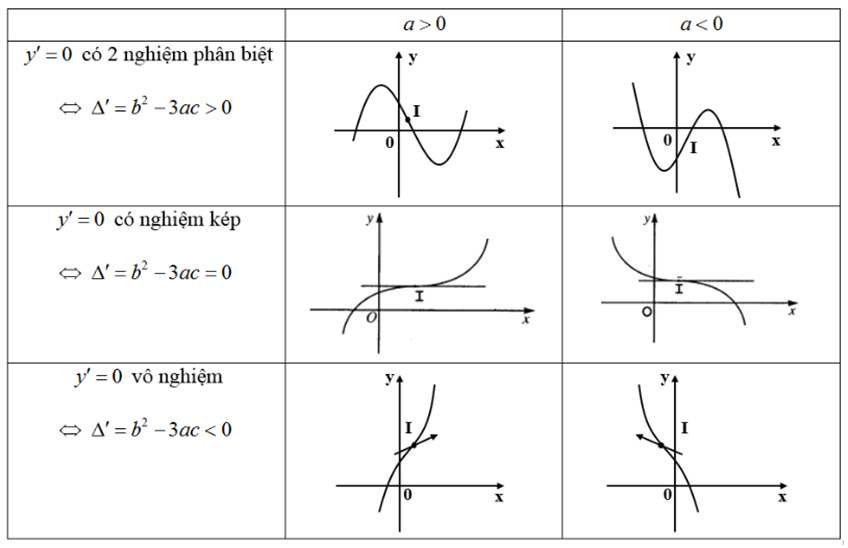
Trường hợp đồ thị có hai điểm cực trị:

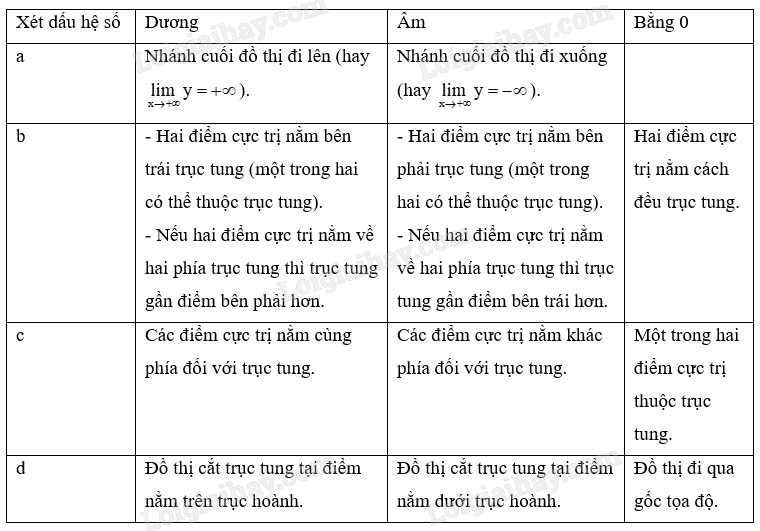
Ví dụ minh hoạ:

Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?

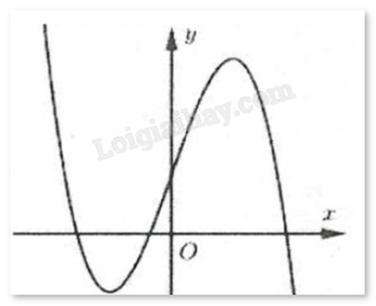
A. $y =  - {x^3} + 3{x^2} + 1$

B. $y =  - {x^3} + 3x + 1$

C. $y = {x^3} - 3x + 1$

D. $y =  - {x^3} - 3x + 1$

Giải:

Dựa vào đồ thị ta thấy $\mathop {\lim }\limits_{x \to  + \infty } y =  - \infty$ nên hệ số a < 0. Loại đáp án C.

Hàm số có hai điểm cực trị ${x_1} < 0 < {x_2}$ nên y’ = 0 có hai nghiệm trái dấu.

Xét đáp án A, có $y' =  - 3{x^2} + 6x = 0 \Leftrightarrow$ x = 0 hoặc x = 2 (loại).

Xét đáp án D, có $y' =  - 3{x^2} - 3x < 0$ $(\forall x \in \mathbb{R})$ (loại).

Vậy đáp án B đúng.

Cho đồ thị hàm số $y = \frac{{ax + b}}{{cx + d}}$ $(c \ne 0,ad - bc \ne 0)$.

Hàm số đồng biến trên tập xác định: ad – bc > 0.

Hàm số nghịch biến trên tập xác định: ad – bc < 0.

Đồ thị hàm số cắt trục Oy tại điểm có tung độ $y = \frac{b}{d}$.

Đường tiệm cận đứng của đồ thị nằm bên phải trục tung: $x =  - \frac{d}{c}$.                                                                                                                

Đường tiệm cận ngang của đồ thị nằm phía dưới trục hoành: $y = \frac{a}{c}$.

Đồ thị hàm số đi qua điểm $A\left( {{x_A};{y_A}} \right)$ thì $f\left( {{x_A}} \right) = {y_A} \Leftrightarrow \frac{{a{x_A} + b}}{{c{x_A} + d}} = {y_A}$.

Ví dụ minh hoạ:

Cho hàm số có bảng biến thiên như hình vẽ sau.

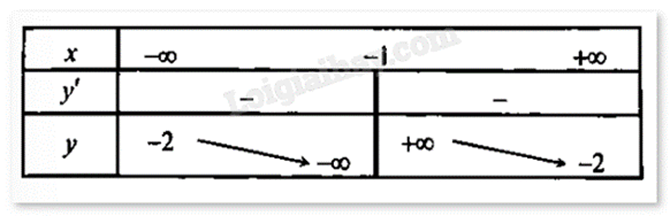
Xác định công thức của hàm số.

A. $y = \frac{{x - 4}}{{2x + 2}}$

B. $y = \frac{{ - 2x - 4}}{{x + 1}}$

C. $y = \frac{{ - 2x + 3}}{{x + 1}}$

D. $y = \frac{{2 - x}}{{x + 1}}$

Giải:

Đồ thị hàm số có tiệm cận đứng x = -1 và tiệm cận ngang y = -2. Loại A và D.

Xét hàm số $y = \frac{{ - 2x - 4}}{{x + 1}}$ có $y' = \frac{2}{{{{(x + 1)}^2}}} > 0$. Hàm số đồng biến trên các khoảng xác định.

Xét hàm số $y = \frac{{ - 2x + 3}}{{x + 1}}$ có $y' = \frac{{ - 5}}{{{{(x + 1)}^2}}} < 0$. Hàm số nghịch biến trên các khoảng xác.

Mà theo bảng biến thiên thì hàm số nghịch biến. Ta chọn hàm số $y = \frac{{ - 2x + 3}}{{x + 1}}$.