Đề thi vào 10 môn Toán Bạc Liêu năm 2025

Đề bài

Câu 1 (0,5 điểm). Giải phương trình: $\left( {2x - 3} \right)\left( {x + 5} \right) = 0$.

Câu 2 (1,5 điểm). 

a) Tính giá trị của biểu thức: $A = \sqrt {49}  - \sqrt {25}$.

b) Cho biểu thức $B = \frac{{\sqrt x }}{{\sqrt x  - 6}} - \frac{6}{{\sqrt x  + 6}}$ (với $x \ge 0;x \ne 36$).

Rút gọn biểu thức B và tính giá trị của biểu thức B khi $x = 6$.

Câu 3 (1,5 điểm). Cho hàm số $y = \frac{2}{3}{x^2}$.

a) Tìm hệ số a của ${x^2}$.

b) Vẽ đồ thị của hàm số đã cho.

Câu 4 (1,5 điểm). Cho phương trình bậc hai $2{x^2} + 3x - 2 = 0$

a) Xác định các hệ số $a,b,c$ của phương trình.

b) Giải phương trình đã cho.

Câu 5 (1,0 điểm). Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Tính xác suất của biến cố A: “Tổng số chấm xuất hiện trên hai mặt con xúc xắc bằng 5”.

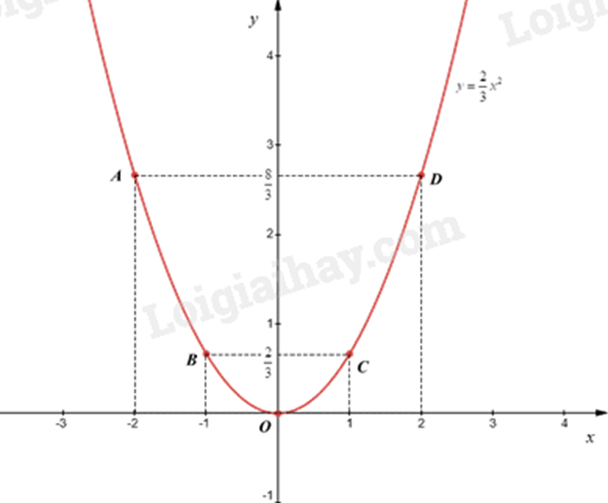
Câu 6 (1,0 điểm). Để chuẩn bị khen thưởng cho học sinh cuối năm học, Trường THCS X cần mua 1400 quyển vở và 700 cây bút ở Nhà sách Y để làm phần thưởng. Nhà trường dự tính mua với giá niêm yết sẽ cần 22 triệu 400 nghìn đồng, nhưng do mua với số lượng lớn nên Nhà sách Y đã giảm giá $5{\rm{\% }}$ cho mỗi quyển vở và $10{\rm{\% }}$ cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng. Tính giá tiền niêm yết của mỗi quyển vở và mỗi cây bút.

Câu 7 (0,5 điểm). Một tam giác vuông có cạnh huyền dài 13cm và diện tích bằng $30{m^2}$. Lập phương trình bậc hai một ẩn có hai nghiệm là độ dài hai cạnh góc vuông của tam giác đã cho.

Câu 8 (2,5 điểm). Cho đường tròn (O; R) có đường kính AB vuông góc với dây cung CD tại điểm I (I nằm giữa A và O). Lấy điểm E bất kỳ trên cung nhỏ BC (E khác B và C). Hai đoạn thẳng AE và CD cắt nhau tại K.

a) Chứng minh tứ giác KEBI là tứ giác nội tiếp.

b) Chứng minh: $AK \cdot AE = AB \cdot AI$.

c) Gọi P là giao điểm cùa tia BE và tia DC, Q là giao điểm của hai đường thẳng AP và BK. Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp $\Delta PQE$.

-------- Hết --------

Lời giải chi tiết

Câu 1 (0,5 điểm). Giải phương trình: $\left( {2x - 3} \right)\left( {x + 5} \right) = 0$.

Lời giải:

$\left( {2x - 3} \right)\left( {x + 5} \right) = 0$

Phương trình tích có hai nghiệm thoả mãn:

+) $2x - 3 = 0$ suy ra $x = \frac{3}{2}$

+) $x + 5 = 0$ suy ra $x =  - 5$

Vậy phương trình có hai nghiệm $x = \frac{3}{2}$ và $x =  - 5$

Câu 2 (1,5 điểm). a) Tính giá trị của biểu thức: $A = \sqrt {49}  - \sqrt {25}$.

b) Cho biểu thức $B = \frac{{\sqrt x }}{{\sqrt x  - 6}} - \frac{6}{{\sqrt x  + 6}}$ (với $x \ge 0;x \ne 36$).

Rút gọn biểu thức B và tính giá trị của biểu thức B khi $x = 6$.

Lời giải:

a) Ta có: $A = \sqrt {49}  - \sqrt {25}  = 7 - 5 = 2$.

b) +) ĐKXĐ: $x \ge 0;x \ne 36$

$\begin{array}{l}B = \frac{{\sqrt x }}{{\sqrt x  - 6}} - \frac{6}{{\sqrt x  + 6}}\\ = \frac{{\sqrt x \left( {\sqrt x  + 6} \right)}}{{\left( {\sqrt x  - 6} \right)\left( {\sqrt x  + 6} \right)}} - \frac{{6\left( {\sqrt x  - 6} \right)}}{{\left( {\sqrt x  - 6} \right)\left( {\sqrt x  + 6} \right)}}\\ = \frac{{x + 6\sqrt x  - \left( {6\sqrt x  - 36} \right)}}{{\left( {\sqrt x  - 6} \right)\left( {\sqrt x  + 6} \right)}}\\ = \frac{{x + 6\sqrt x  - 6\sqrt x  + 36}}{{\left( {\sqrt x  - 6} \right)\left( {\sqrt x  + 6} \right)}}\\ = \frac{{x + 36}}{{x - 36}}\end{array}$

Vậy $B = \frac{{x + 36}}{{x - 36}}$ với $x \ge 0;x \ne 36$.

+) Thay $x = 6$ (TMĐK) vào B, ta được:

$B = \frac{{42}}{{6 - 36}} = \frac{{42}}{{ - 30}} =  - \frac{7}{5}$

Vậy $B =  - \frac{7}{5}$ khi $x = 6$.

Câu 3 (1,5 điểm). Cho hàm số $y = \frac{2}{3}{x^2}$.

a) Tìm hệ số a của ${x^2}$.

b) Vẽ đồ thị của hàm số đã cho.

Lời giải:

a) Hệ số a của ${x^2}$ là $a = \frac{2}{3}$.

b) Ta có bảng giá trị sau:

Đồ thị hàm số là đường cong parabol đi qua các điểm $O\,\left( {0;0} \right);A\left( { - 2;\frac{8}{3}} \right);\,\,B\left( { - 1;\frac{2}{3}} \right);C\left( {1;\frac{2}{3}} \right);\,\,D\left( {2;\frac{8}{3}} \right)$

Ta vẽ được đồ thị hàm số $y = \frac{2}{3}{x^2}$ như sau:

Câu 4 (1,5 điểm). Cho phương trình bậc hai $2{x^2} + 3x - 2 = 0$

a) Xác định các hệ số $a,b,c$ của phương trình.

b) Giải phương trình đã cho.

Lời giải:

a) Phương trình $2{x^2} + 3x - 2 = 0$ có $a = 2;b = 3;c =  - 2.$

b) Ta có $\Delta  = {b^2} - 4ac = 9 - 4.2.\left( { - 2} \right) = 25 > 0$

Phương trình có hai nghiệm phân biệt:

${x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}} = \frac{{ - 3 + 5}}{{2.2}} = \frac{1}{2}$ và $x_2^{} = \frac{{ - b - \sqrt \Delta  }}{{2a}} = \frac{{ - 3 - 5}}{{2.2}} =  - 2$.

Vậy phương trình có hai nghiệm $x \in \left\{ {\frac{1}{2}; - 2} \right\}.$

Câu 5 (1,0 điểm). Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Tính xác suất của biến cố A: “Tổng số chấm xuất hiện trên hai mặt con xúc xắc bằng 5”.

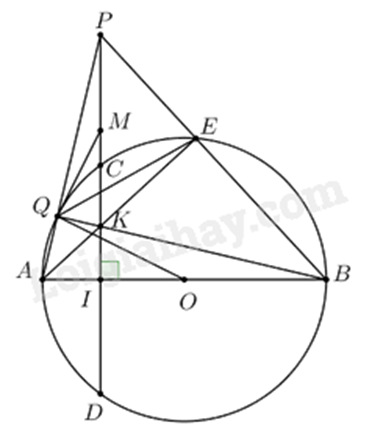
Lời giải:

Gieo đồng thời hai con con xúc xắc có 36 kết quả có thể xảy ra.

Biến cố A: “Tổng số chấm xuất hiện trên hai mặt con xúc xắc bằng 5”

Ta có $A = \left\{ {(1;4),(2;3),(3;2),(4;1)} \right\}$, suy ra có 4 kết quả có thể xảy ra biến cố A.

Xác suất của biến cố $A$ là $\frac{4}{{36}} = \frac{1}{9}.$

Câu 6 (1,0 điểm). Để chuẩn bị khen thưởng cho học sinh cuối năm học, Trường THCS X cần mua 1400 quyển vở và 700 cây bút ở Nhà sách Y để làm phần thưởng. Nhà trường dự tính mua với giá niêm yết sẽ cần 22 triệu 400 nghìn đồng, nhưng do mua với số lượng lớn nên Nhà sách Y đã giảm giá $5{\rm{\% }}$ cho mỗi quyển vở và $10{\rm{\% }}$ cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng. Tính giá tiền niêm yết của mỗi quyển vở và mỗi cây bút.

Lời giải:

Gọi giá niêm yết của mỗi quyển vở và mỗi cây bút lần lượt là $x$,$y$ (đồng, $0 < x,y < 22400000$)

Nhà trường dự tính mua 1400 quyển vở và 700 cây bút với giá niêm yết sẽ cần 22 triệu 400 nghìn đồng nên ta có phương trình $1400x + 700y = 22400000$ hay $2x + y = 32000$ (1)

Nhà sách Y đã giảm giá $5{\rm{\% }}$ cho mỗi quyển vở và $10{\rm{\% }}$ cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng nên ta có phương trình:

$1400x.(100\%  - 5\% ) + 700y.(100\%  - 10\% ) = 21000000$ hay $19x + 9y = 300000$ (2)

Từ (1) và (2) ta có hệ phương trình:

$\left\{ \begin{array}{l}2x + y = 32000\\19x + 9y = 300000\end{array} \right.$

$\left\{ \begin{array}{l}18x + 9y = 288000\\19x + 9y = 300000\end{array} \right.$

$\left\{ \begin{array}{l}x = 12000\\19x + 9y = 300000\end{array} \right.$

$\left\{ \begin{array}{l}x = 12000\\y = 8000\end{array} \right.\,\,(tm)$

Vậy giá niêm yết của mỗi quyển vở là 12000 (đồng) và mỗi cây bút là 8000 (đồng).

Câu 7 (0,5 điểm). Một tam giác vuông có cạnh huyền dài 13cm và diện tích bằng $30{m^2}$. Lập phương trình bạc hai một ẩn có hai nghiệm là độ dài hai cạnh góc vuông của tam giác đã cho.

Lời giải:

Gọi độ dài hai cạnh góc vuông lần lượt là $x,y{\rm{ cm}},$$0 < x,y < 13$.

Đổi $30{m^2} = 300000\,c{m^2}$

Diện tích tam giác là $300000c{m^2}$ suy ra 

$\begin{array}{l}\frac{1}{2}x.y = 300000\\xy = 600000\end{array}$

Vì cạnh huyền là 13 cm nên theo định lý Pythagore, ta có

$\begin{array}{l}{x^2} + {y^2} = {13^2} = 169\\{\left( {x + y} \right)^2} - 2xy = 169\\{\left( {x + y} \right)^2} - 1200000 = 169\\{\left( {x + y} \right)^2} = 1200169\end{array}$

Suy ra $x + y = \sqrt {1200169}$

Vậy phương trình cần tìm là ${x^2} - \sqrt {1200169} x + 600000 = 0$

Đây là lời giải của HocTot.Nam.Name.Vn theo đúng đề bài gốc của tỉnh Bạc Liêu. Tuy nhiên phương trình tìm được là phương trình vô nghiệm.

Câu 8 (2,5 điểm). Cho đường tròn (O; R) có đường kính AB vuông góc với dây cung CD tại điểm I (I nằm giữa A và O). Lấy điểm E bất kỳ trên cung nhỏ BC (E khác B và C). Hai đoạn thẳng AE và CD cắt nhau tại K.

a) Chứng minh tứ giác KEBI là tứ giác nội tiếp.

b) Chứng minh: $AK \cdot AE = AB \cdot AI$.

c) Gọi P là giao điểm cùa tia BE và tia DC, Q là giao điểm của hai đường thẳng AP và BK. Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp $\Delta PQE$.

Lời giải:

a) Do $\widehat {AEB} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Nên $\Delta KEB$ vuông tại E. Khi đó K, E, B cùng thuộc đường tròn đường kính KB

Tương tự $\Delta KIB$ vuông tại I nên K, I, B cùng thuộc đường tròn đường kính KB

Suy ra K, E, B, I cùng thuộc đường tròn đường kính KB.

Vậy tứ giác KEBI là tứ giác nội tiếp.

b) Xét $\Delta AKI$ và $\Delta ABE$ có

$\widehat {BAE}$ là góc chung

$\widehat {AIK} = \widehat {AEB}\left( { = 90^\circ } \right)$

Suy ra $\Delta AKI\backsim \Delta ABE\left( g.g \right)$

Khi đó $\frac{{AK}}{{AB}} = \frac{{AI}}{{AE}}$ (cặp cạnh tương ứng) hay $AE.AK = AI.AB$ (đpcm)

c) Xét $\Delta ABP$ có $AE \bot PB;PI \bot AB,$ AE và PI cắt nhau tại K nên K là trực tâm của $\Delta ABP$

Suy ra $BK \bot AP$ tại Q (Tính chất đồng quy của 3 đường cao)

Khi đó $\Delta PQK$ vuông tại Q nên P, Q, K cùng thuộc đường tròn đường kính PK

Tương tự $\Delta PEK$ vuông tại E nên P, E, K cùng thuộc đường tròn đường kính PK

Vậy P, Q, K, E cùng thuộc đường tròn đường kính PK.

Gọi M là trung điểm của PK. Khi đó M là tâm đường tròn ngoại tiếp $\Delta PEQ$

Ta có $MP = MQ$  nên $\Delta MPQ$ cân tại M nên $\widehat {MQP} = \widehat {MPQ}$   (1)

Do $BQ \bot AQ\left( {cmt} \right)$ nên $\Delta ABQ$ vuông tại Q, trung tuyến OQ nên $OQ = OA = OB$

Suy ra $\Delta OAQ$ cân tại O nên $\widehat {OQA} = \widehat {OAQ}$    (2)

Từ (1) và (2) suy ra $\widehat {MQP} + \widehat {OQA} = \widehat {MPQ} + \widehat {OAQ} = 90^\circ$ (do $\Delta API$ vuông tại I)

Suy ra $\widehat {OQM} = 180^\circ  - \left( {\widehat {MQP} + \widehat {OQA}} \right) = 180^\circ  - 90^\circ  = 90^\circ$

Suy ra $OQ \bot MQ$ tại $Q \in \left( M \right)$

Vậy OQ là tiếp tuyến của đường tròn ngoại tiếp $\Delta PQE$.