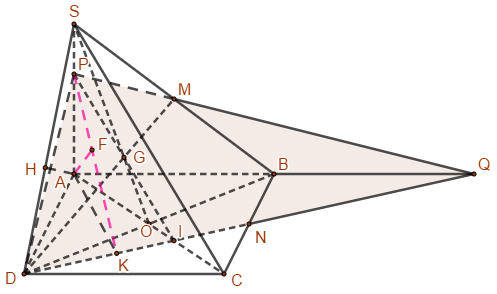
Giải đề thi học kì 2 toán lớp 11 năm 2020 - 2021 trường THPT Trần PhúLàm bàiCâu hỏi 1 : Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 2x} - x} \right)\) Phương pháp giải: Nhân liên hợp với \(\sqrt {{x^2} + 2x} + x\). Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 2x} - x} \right)\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{{{\left( {\sqrt {{x^2} + 2x} } \right)}^2} - {x^2}}}{{\sqrt {{x^2} + 2x} + x}}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{2x}}{{\sqrt {{x^2} + 2x} + x}}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{2x}}{{x\left( {\sqrt {1 + \dfrac{2}{x}} + 1} \right)}}\\ = \dfrac{2}{{1 + 1}} = 1\end{array}\) Câu hỏi 2 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {6{x^2} - 2} - 2}}{{x - 1}}khi{\rm{ }}x > 1\\{a^2}x + 2a{\rm{ khi }}x \le 1\end{array} \right.\). Tìm a để hàm số f(x) liên tục tại điểm x=1. Phương pháp giải: \(f\left( x \right)\) liên tục tại \({x_0}\)khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x \right) = f\left( {{x_0}} \right)\) Lời giải chi tiết: \(\begin{array}{l}f\left( 1 \right) = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = {a^2} + 2a\\\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\sqrt {6{x^2} - 2} - 2}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{6\left( {{x^2} - 1} \right)}}{{\left( {x - 1} \right)\left( {\sqrt {6{x^2} - 2} + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{6\left( {x + 1} \right)}}{{\sqrt {6{x^2} - 2} + 2}}\\ = \dfrac{{6\left( {1 + 1} \right)}}{{\sqrt {6 - 2} + 2}} = 3\end{array}\) \(f\left( x \right)\) liên tục tại x=1 \(\begin{array}{l} \Leftrightarrow {a^2} + 2x = 3\\ \Leftrightarrow \left[ \begin{array}{l}a = 1\\a = - 3\end{array} \right.\end{array}\) Câu hỏi 3 : Viết phương trình tiếp tuyến \(\left( \Delta \right)\) của đồ thị hàm số \(y = {x^3} - 3{x^2} - 3x\), biết tiếp tuyến song song với đường thẳng (D) có phương trình \(y = 6x + 5\). Phương pháp giải: Tính y’ \(\left( \Delta \right)//\left( d \right) \Rightarrow \) cùng hệ số góc. Hệ số góc của tiếp tuyến của đồ thị \(y = f\left( x \right)\) tại \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là \(f'\left( {{x_0}} \right)\). Giải phương tình \(f'\left( {{x_0}} \right) = 6\) Phương trình tiếp tuyến của đồ thị \(y = f\left( x \right)\) tại \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là: \(y = f'\left( {{x_0}} \right).\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\) Lời giải chi tiết: Gọi \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là tiếp điểm của tiếp tuyến cần tìm. Ta có \(\left( \Delta \right)//\left( d \right) \Rightarrow \)\(f'\left( {{x_0}} \right)\) \(\begin{array}{l} \Leftrightarrow 3{x_0}^2 - 6{x_0} - 3 = 6\\ \Leftrightarrow x_0^2 - 2{x_0} - 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = - 1\\{x_0} = 3\end{array} \right.\end{array}\) Với \({x_0} = - 1\) Ta có: \(f\left( {{x_0}} \right) = - 1\). Phương trình tiếp tuyến: \(y = 6\left( {x + 1} \right) - 1 = 6x + 5\left( L \right)\) Với \({x_0} = 3\) Ta có: \(f\left( {{x_0}} \right) = - 9\). Phương trình tiếp tuyến: \(y = 6\left( {x - 3} \right) - 9 = 6x - 27\) Vậy tiếp tuyến cần tìm là \(y = 6x - 27\). Câu hỏi 4 : Tính đạo hàm của hàm số \(y = \dfrac{{\sin 2x + 2}}{{\cos 2x + 3}}\). Phương pháp giải: Sử dụng các quy tắc tính đạo hàm: \({\left( {\dfrac{u}{v}} \right)^\prime } = \dfrac{{u'v - v'u}}{{{v^2}}}\) \(\begin{array}{l}\left[ {\cos \left( {ax + b} \right)} \right]' = - a.\sin \left( {ax + b} \right)\\\left[ {\sin \left( {ax + b} \right)} \right]' = a.\cos \left( {ax + b} \right)\end{array}\) Lời giải chi tiết: \(\begin{array}{l}y' = \dfrac{{2cox2x\left( {\cos 2x + 3} \right) + 2\sin 2x\left( {\sin 2x + 2} \right)}}{{{{\left( {\cos 2x + 3} \right)}^2}}}\\ = \dfrac{{2\left( {{{\cos }^2}2x + {{\sin }^2}2x} \right) + 6\cos 2x + 4\sin 2x}}{{{{\left( {\cos 2x + 3} \right)}^2}}}\\ = \dfrac{{2\left( {3\cos 2x + 2\sin 2x + 1} \right)}}{{{{\left( {\cos 2x + 3} \right)}^2}}}\end{array}\) Câu hỏi 5 : Tính đạo hàm của hàm số \(y = \tan 2x + {\cot ^2}x\). Phương pháp giải: Sử dụng các công thức: \(\begin{array}{l}\left( {\tan ax} \right)' = a.\left( {1 + {{\tan }^2}ax} \right)\\\left( {{u^\alpha }} \right)' = \alpha .{u^{\alpha - 1}}.u'\\\left( {\cot x} \right)' = - \left( {1 + {{\cot }^2}x} \right)\end{array}\) Lời giải chi tiết: \(\begin{array}{l}y' = \dfrac{2}{{{{\cos }^2}2x}} + 2.\cot x.\dfrac{{ - 1}}{{{{\sin }^2}x}}\\ = \dfrac{2}{{{{\cos }^2}2x}} - \dfrac{{2\cos x}}{{{{\sin }^3}x}}\end{array}\) Câu hỏi 6 : Cho hàm số \(f\left( x \right) = \left( {x - 2} \right)\sqrt {{x^2} - 1} \), tính đạo hàm \(f'\left( x \right)\) và giải bất phương trình \(f'\left( x \right) \le \sqrt {{x^2} - 1} \) Phương pháp giải: Chuyển vế rồi quy đồng. \(\dfrac{{f\left( x \right)}}{{\sqrt {g\left( x \right)} }} \le 0 \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \le 0\\g\left( x \right) > 0\end{array} \right.\) Lời giải chi tiết: \(\begin{array}{l}f'\left( x \right) = \sqrt {{x^2} - 1} + \left( {x - 2} \right).\dfrac{x}{{\sqrt {{x^2} - 1} }}\\ = \dfrac{{\left( {{x^2} - 1} \right) + \left( {x - 2} \right).x}}{{\sqrt {{x^2} - 1} }}\\ = \dfrac{{2{x^2} - 2x - 1}}{{\sqrt {{x^2} - 1} }}\\f'\left( x \right) \le \sqrt {{x^2} - 1} \\ \Leftrightarrow \dfrac{{2{x^2} - 2x - 1}}{{\sqrt {{x^2} - 1} }} \le \sqrt {{x^2} - 1} \\ \Leftrightarrow \dfrac{{2{x^2} - 2x - 1}}{{\sqrt {{x^2} - 1} }} - \sqrt {{x^2} - 1} \le 0\\ \Leftrightarrow \dfrac{{2{x^2} - 2x - 1 - \left( {{x^2} - 1} \right)}}{{\sqrt {{x^2} - 1} }} \le 0\\ \Leftrightarrow \dfrac{{{x^2} - 2x}}{{\sqrt {{x^2} - 1} }} \le 0 \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2x \le 0\\{x^2} - 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 2\\\left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\end{array} \right. \Leftrightarrow 1 < x \le 2\\ = > S = \left( {1;2} \right]\end{array}\) Câu hỏi 7 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với mặt phẳng (ABCD). Biết SA=\(a\sqrt 3 \), AB=\(a\) và BC=\(2a\sqrt 2 \). a. Xác định và tính góc giữa đường thẳng SC và mặt phẳng đáy (ABCD). b. Xác định và tính góc giữa hai mặt phẳng (SBC) và mặt đáy (ABCD). c. Tính khoảng cách từ điểm A đến mặt phẳng (SCD). d. Tính khoảng cách giữa hai đường thẳng SC và MD, M là trung điểm của SB. Phương pháp giải: a. - Tìm hình chiếu của SC lên (ABCD). - Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. b. - Xác định mặt phẳng vuông góc với (SBC) và (ABCD). - Xác định các giao tuyến của mặt phẳng này với từng mặt phẳng (SBC) và (ABCD). - Góc giữa 2 giao tuyến bằng góc giữa (SBC) và (ABCD). c. - Kẻ \(AH \bot SD\). - Chứng minh \(AH \bot \left( {SCD} \right)\) d. - Tìm mặt phẳng \(\left( \alpha \right)\) qua MD và song song với SC. - Xây dựng mối quan hệ giữa \(d\left( {SC,MD} \right)\) và \(d\left( {A,\left( \alpha \right)} \right)\). - Hệ thức lượng trong tam giác ABC vuông tại A có chiều cao AH: \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{C^2}}} + \dfrac{1}{{A{B^2}}}\). Lời giải chi tiết:
a. ta có \(SA \bot \left( {ABCD} \right)\) => A là hình chiếu của S lên (ABCD). => AC là hình chiếu của SC lên (ABCD). => Góc giữa SC và (ABCD) là góc giữa SC và AC và bằng \(\widehat {SCA}\). Ta có ABCD là hình chữ nhật nên \(AC = \sqrt {A{B^2} + B{C^2}} = 3a\) \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{\sqrt 3 }}{3} = > \widehat {SCA} = 30^\circ \) Vậy góc giữa SC và (ABCD) là \(30^\circ \). b. ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) =>\(BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\) Mà \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right.\) => Góc giữa (SBC) và (ABCD) là \(\widehat {SBA}\) \(\tan \widehat {SBA} = \dfrac{{SA}}{{BA}} = \sqrt 3 \Rightarrow \widehat {SBA} = 60^\circ \). Vậy góc giữa (SBC) và (ABCD) là \(60^\circ \). c. Ta có \(CD \bot SA\) ( do \(SA \bot \left( {ABCD} \right)\)). \(\begin{array}{l}CD \bot AD\\ \Rightarrow CD \bot \left( {SAD} \right)\\ \Rightarrow \left( {SCD} \right) \bot \left( {SAD} \right)\\\left( {SCD} \right) \cap \left( {SAD} \right) = SD\end{array}\) Kẻ AH vuông góc với SD => \(AH \bot \left( {SCD} \right) = > AH = d\left( {A,\left( {SCD} \right)} \right)\) \(\begin{array}{l}\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}} = \dfrac{{11}}{{24{a^2}}}\\ \Rightarrow AH = \dfrac{{2a\sqrt {66} }}{{11}}\end{array}\) Vậy \(d\left( {A,\left( {SCD} \right)} \right) = \dfrac{{2a\sqrt {66} }}{{11}}\) d. Gọi O là giao của AC và BD, G là giao của SO và MD. Khi đó \(G \in MD\). Trong (SAC), qua G kẻ PI//SC với \(P \in SA,I \in AC\). Kéo dài DI cắt AB tại Q., BC tại N. Kẻ AK vuông góc với DQ. Kẻ AF vuông góc với PK. Ta có PI//SC và \(PI \cap MD = \left\{ G \right\}\) nên SC//(PMID) \(MN//SC\) do MN là đường trung tuyến của tam giác SBC. \(Q \in \left( {PMID} \right)\) do \(Q \in DI\). =>SC//(PDP) Ta có \(\begin{array}{l}\left. \begin{array}{l}\left\{ \begin{array}{l}AK \bot DQ\\PA \bot DQ\end{array} \right. \Rightarrow DQ \bot \left( {PAK} \right)\\ \Rightarrow \left( {PAK} \right) \bot \left( {PDQ} \right)\\\left( {PAK} \right) \cap \left( {PDQ} \right) = PK\\AF \bot PK\end{array} \right\}\\ \Rightarrow AF \bot \left( {PQD} \right)\\ \Leftrightarrow AF = d\left( {A,\left( {PQD} \right)} \right)\end{array}\) Ta có G là trọng tâm tam giác SBD nên \(\dfrac{{SG}}{{SO}} = \dfrac{2}{3}\) => G là trọng tâm tam giác SAC vì O là trung điểm của AC. \( = > \dfrac{{AP}}{{AS}} = \dfrac{{AI}}{{AC}} = \dfrac{2}{3}\) \(\begin{array}{l} = > d\left( {SC,MD} \right) = d\left( {SC,\left( {PDQ} \right)} \right)\\ = d\left( {S,\left( {PQD} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {PQD} \right)} \right)\\ = > d\left( {SC,MD} \right) = \dfrac{1}{2}AF\end{array}\) Ta có \(\dfrac{{AI}}{{AC}} = \dfrac{2}{3} = > AD = 2CN\)=> N là trung điểm của BC. \(\begin{array}{l} = > {\rm{ }}DQ = 2DN = 2.\sqrt {2{a^2} + {a^2}} = 2a\sqrt 3 \\ = > AQ = \sqrt {12{a^2} - 8{a^2}} = 2a\\ = > \dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{A{Q^2}}} = \dfrac{3}{{8{a^2}}}\\ = > \dfrac{1}{{A{F^2}}} = \dfrac{1}{{A{K^2}}} + \dfrac{1}{{A{P^2}}}\\ = \dfrac{3}{{8{a^2}}} + \dfrac{1}{{{{\left( {\dfrac{2}{3}.a\sqrt 3 } \right)}^2}}} = \dfrac{9}{{8{a^2}}}\\ = > AF = \dfrac{{2a\sqrt 2 }}{3}\\ = > d\left( {SC,MD} \right) = \dfrac{{a\sqrt 2 }}{3}\end{array}\)
|