Giải đề thi học kì 2 toán lớp 11 năm 2020 - 2021 sở GD&ĐT Quảng NamLàm bàiCâu hỏi 1 : Tìm đạo hàm của hàm số \(y = 2\cos x\)
Đáp án: D Phương pháp giải: \(\left( {\cos x} \right)' = - \sin x\) Lời giải chi tiết: \({(2\cos x)^\prime } = 2.\left( {\cos x} \right)' = - 2\sin x\) Câu hỏi 2 : Tìm đạo hàm của hàm số \(y = \tan x\) với \(x \ne \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
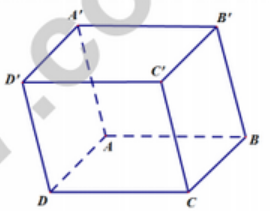
Đáp án: D Phương pháp giải: Đạo hàm của hàm lượng giác. Lời giải chi tiết: \(y' = \dfrac{1}{{{{\cos }^2}x}}\) Câu hỏi 3 : Cho hình hộp ABCD.A’B’C’D’ (hình vẽ minh họa).
Mệnh đề nào sau đây đúng?
Đáp án: B Phương pháp giải: Sử dụng quy tắc hình bình hành. Lời giải chi tiết: ACC’A’ và ABCD là hình bình hành nên: \(\overrightarrow {A{C^\prime }} = \overrightarrow {AC} + \overrightarrow {A{A^\prime }} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} \) Câu hỏi 4 : Trong không gian, cho đoạn thẳng AB có trung điểm là I, \((\alpha )\) là mặt phẳng trung trực của đoạn thẳng AB. Phát biểu nào sau đây đúng?
Đáp án: A Phương pháp giải: Định nghĩa mặt phẳng trung trực. Lời giải chi tiết: Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng vuông góc với AB tại trung điểm của AB. Câu hỏi 5 : Hàm số nào dưới đây liên tục trên toàn bộ tập số thực \(\mathbb{R}\) ?
Đáp án: C Phương pháp giải: Hàm đa thức luôn liên tục trên \(\mathbb{R}\) Lời giải chi tiết: \(y = {x^2} - 3x + 56\) là hàm đa thức nên liên tục trên \(\mathbb{R}\). Câu hỏi 6 : Mệnh đề nào sau đây sai?
Đáp án: B Phương pháp giải: Sử dụng quy tắc đạo hàm các hàm cơ bản. Lời giải chi tiết: B sai vì \(\left( {\sqrt x } \right)' = \dfrac{1}{{2\sqrt x }}\). Câu hỏi 7 : \(\mathop {\lim }\limits_{x \to {2^2}} \dfrac{{2x - 5}}{{x - 2}}\) bằng
Đáp án: A Phương pháp giải: \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = L < 0;\mathop {\lim }\limits_{x \to {x_0}^ + } g\left( x \right) = 0\) và \(g\left( x \right) > 0\) khi \(x \to {x_0}^ + \) thì \(\mathop {\lim }\limits_{x \to x_0^ + } \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = - \infty \) Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^2}} 2x - 5 = - 1 < 0\\\mathop {\lim }\limits_{x \to {2^2}} \left( {x - 2} \right) = 0;\\x - 2 > 0\forall x > 2\end{array}\) \( \Rightarrow \mathop {\lim }\limits_{x \to {2^2}} \dfrac{{2x - 5}}{{x - 2}} = - \infty \) Câu hỏi 8 : Gọi \({\rm{S}}\) là tổng của cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) có công bội \(q(|q| < 1)\). Khẳng định nào sau đây đúng ?
Đáp án: A Phương pháp giải: Lý thuyết tổng cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) có công bội \(q(|q| < 1)\). Lời giải chi tiết: \(\begin{array}{l}S = {u_1} + {u_2} + ...\\ = {u_1}\left( {1 + q + {q^2} + ...} \right)\\ = \dfrac{{{u_1}}}{{1 - q}}\end{array}\) Câu hỏi 9 : Cho hai hàm số \(u = u(x),v = v(x)\) có đạo hàm tại điểm \(x\) thuộc khoảng xác định. Mệnh đề nào sau đây sai ?
Đáp án: D Phương pháp giải: Sử dụng quy tắc đạo hàm của tổng hiệu, tích. Lời giải chi tiết: D sai vì \(\left( {u.v} \right)' = u'.v + v'.u\) Câu hỏi 10 : Cho hai hàm số \(f(x),g(x)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f(x) = - 5\) và \(\mathop {\lim }\limits_{x \to 1} g(x) = 2\). Giá trị của \(\mathop {\lim }\limits_{x \to 1} [f(x) - g(x)]\) bằng
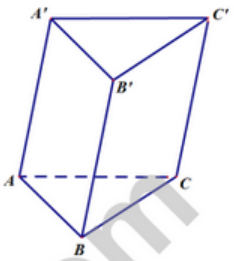
Đáp án: C Phương pháp giải: \(\mathop {\lim }\limits_{x \to {x_0}} [f(x) - g(x)] = \mathop {\lim }\limits_{x \to {x_0}} f(x) - \mathop {\lim }\limits_{x \to {x_0}} g(x)\) Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} [f(x) - g(x)]\\ = \mathop {\lim }\limits_{x \to 1} f(x) - \mathop {\lim }\limits_{x \to 1} g(x)\\ = - 5 - 2 = - 7\end{array}\) Câu hỏi 11 : Cho lăng trụ ABC.A’B’C’(hình vẽ minh họa)
Vecto \(\overline {{A^\prime }A} \) không phải là vecto chỉ phương của đường thẳng nào sau đây?
Đáp án: C Phương pháp giải: \(\overrightarrow {{A^\prime }A} \) là vecto chỉ phương của mọi đường thẳng song song với \({A^\prime }A\) Lời giải chi tiết: BC không song song với \(AA'\) nên BC không nhận \(AA'\) làm vecto chỉ phương. Câu hỏi 12 : Trong không gian, cho hai đường thẳng phân biệt a, b và mặt phẳng \(\alpha \). Phát hiểu nào sau đây đúng?
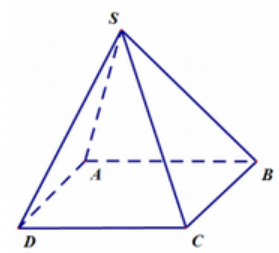
Đáp án: C Phương pháp giải: Lý thuyết đường thẳng vuông góc với mặt phẳng. Lời giải chi tiết: Nếu \(b//(\alpha )\) và \(a \bot (\alpha )\) thì \(a \bot b\). Câu hỏi 13 : Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA vuông góc với mặt phẳng (ABCD) (như hình vẽ minh họa)
Hãy chọn khẳng định đúng?
Đáp án: A Phương pháp giải: 2 đường chéo của hình thoi vuông góc với nhau. Lời giải chi tiết: ABCD là hình thoi nên \(BD \bot AC\). Mà \(BD \bot SA\) và AC và SA cắt nhau tại A nên \(BD \bot \left( {SAC} \right)\). Câu hỏi 14 : \(\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 4}}{{x - 2}}\) bằng
Đáp án: D Phương pháp giải: Khử mẫu. Thay x=2 tìm giới hạn. Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} - 4}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \left( {x + 2} \right) = 4\end{array}\) Câu hỏi 15 : \(\lim \dfrac{{n + 1}}{{2n - 3}}\) bằng
Đáp án: C Phương pháp giải: Chia cả tử và mẫu cho n. Sử dụng \(\lim \dfrac{1}{n} = 0\) Lời giải chi tiết: \(\lim \dfrac{{n + 1}}{{2n - 3}} = \lim \dfrac{{n\left( {1 + \dfrac{1}{n}} \right)}}{{2\left( {1 - \dfrac{3}{n}} \right)}} = \dfrac{1}{2}\) Câu hỏi 16 : Cho hình chóp S.ABCD có đáy là hình bình hành (hình vẽ minh họa).
Hãy chọn khẳng định đúng.
Đáp án: A Phương pháp giải: M là trung điểm của AB thì \(\overrightarrow {CA} + \overrightarrow {CB} = 2\overrightarrow {CM} \). Lời giải chi tiết: Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm chung của AC và BD. \(\begin{array}{l}\overrightarrow {SC} + \overrightarrow {SA} = 2\overrightarrow {SO} ;\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \\ \Rightarrow \overrightarrow {SC} + \overrightarrow {SA} = \overrightarrow {SB} + \overrightarrow {SD} \end{array}\) Câu hỏi 17 : Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau (hình vẽ minh họa).
Số đo góc giữa hai đường thẳng SA và CD bằng
Đáp án: C Phương pháp giải: Từ một điểm trên a và kẻ đường thẳng c song song với đường thẳng b thì góc giữa a và b bằng góc giữa c và b. Lời giải chi tiết: \(\begin{array}{l}CD||AB \Rightarrow \widehat {\left( {SA,CD} \right)}\\ = \widehat {\left( {SA,AB} \right)} = \widehat {SAB} = 60^\circ \end{array}\) Câu hỏi 18 : Tìm đạo hàm của hàm số \(y = \sqrt {{x^2} + 1} \).
Đáp án: B Phương pháp giải: Sử dụng \(\left( {\sqrt u } \right)' = \dfrac{{u'}}{{2\sqrt u }}\) Lời giải chi tiết: \(y' = \dfrac{{\left( {{x^2} + 1} \right)'}}{{2\sqrt {{x^2} + 1} }} = \dfrac{{2x}}{{2\sqrt {{x^2} + 1} }} = \dfrac{x}{{\sqrt {{x^2} + 1} }}\) Câu hỏi 19 : Cho hàm số \(y = \sin 2x\). Mệnh đề nào sau đây đúng?
Đáp án: C Phương pháp giải: \(\left( {\sin u} \right)' = u'.\cos u\) Thay \(x = \dfrac{\pi }{6}\) vào đạo hàm. Lời giải chi tiết: \(\begin{array}{l}y' = \left( {\sin 2x} \right)' = 2.\cos 2x\\ \Rightarrow y'\left( {\dfrac{\pi }{6}} \right) = 2.\cos \dfrac{\pi }{3} = 1\end{array}\) Câu hỏi 20 : Một chất điểm chuyển động theo phương trình \(S = - \dfrac{1}{3}{t^3} + 6{t^2}\), trong đó \(t > 0,t\) được tính bằng giây \((s)\) và \(S\) tính bằng mét \((m)\). Vận tốc của chất điểm tại thời điểm \(t = 3\) (giây) bằng
Đáp án: C Phương pháp giải: Hàm số của vận tốc: \(v\left( t \right) = S'\left( t \right)\). Thay t=3 vào tính \(v\left( 3 \right)\). Lời giải chi tiết: \(\begin{array}{l}v\left( t \right) = S'\left( t \right) = - {t^2} + 12t\\ \Rightarrow v\left( 3 \right) = - 9 + 36 = 27m/s\end{array}\) Câu hỏi 21 : \(\lim \dfrac{{1 - {3^n}}}{{{2^n} + {{4.3}^n}}}\) bằng
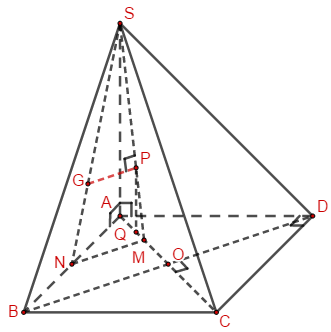
Đáp án: C Phương pháp giải: Chia cả tử và mẫu cho \({3^n}\). \(\lim \dfrac{1}{{{3^n}}} = 0;\lim \dfrac{{{2^n}}}{{{3^n}}} = 0\) Lời giải chi tiết: \(\lim \dfrac{{1 - {3^n}}}{{{2^n} + {{4.3}^n}}} = \lim \dfrac{{\dfrac{1}{{{3^n}}} - 1}}{{\dfrac{{{2^n}}}{{{3^n}}} + 4}} = \dfrac{{ - 1}}{4}\) Câu hỏi 22 : (2 điểm) Câu 1: Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{\sqrt {x + 6} - 2}}{{x + 2}}}&{{\rm{ khi }}x > - 2}\\{x + 2m}&{{\rm{ khi }}x \le - 2}\end{array}} \right.\). Tìm tất cả các giá trị của tham số \(m\) để hàm số \(f(x)\) liên tục tại điểm \(x = - 2\). Phương pháp giải: Lời giải chi tiết: Câu 2: Cho hàm số \(y = f(x) = \dfrac{{2x - 1}}{{x + 1}}\), có đồ thị \((C)\). Viết phương trình tiếp tuyến của đồ thị \((C)\) biết tiếp tuyến vuông góc với đường thẳng \(d:y = - 3x + 4\). Phương pháp giải: Tìm \(f'\left( x \right)\). Tiếp tuyến của hàm số tại \({x_0}\): \(y = f'\left( {{x_0}} \right).\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\). Lời giải chi tiết: \(f'\left( x \right) = \dfrac{3}{{{{\left( {x + 1} \right)}^2}}}\) Tiếp tuyến vuông góc với đường thẳng \(d:y = - 3x + 4\) nên \(\dfrac{3}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{1}{3} \Leftrightarrow \left| {x + 1} \right| = 3\)\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 4\end{array} \right.\) Câu hỏi 23 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB, \(\alpha \) là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Xác định \(\alpha \) và tính \(\sin \alpha \). Phương pháp giải: Xác định đường thẳng qua G và vuông góc với (SAC). Góc giữa CG và (SAC) là góc giữa CG và hình chiếu của nó lên (SAC). Lời giải chi tiết:
Gọi O là tâm của ABCD. M là trung điểm của AO, N là trung điểm của AB. Qua G kẻ GP song song với MN (\(P \in SM\)). Ta có ABCD là hình vuông nên \(BD \bot AC\). Mà \(MN||BD\)\( \Rightarrow MN \bot AC\). Ta lại có \(MN \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\) => \(MN \bot \left( {SAC} \right)\) \(\begin{array}{l}GP||MN \Rightarrow GP \bot \left( {SAC} \right)\\ \Rightarrow \widehat {\left( {CG,\left( {SAC} \right)} \right)} = \widehat {GCP} = \alpha \end{array}\) \(GP = \dfrac{2}{3}MN = \dfrac{2}{3}.\dfrac{1}{2}OB\)\( = \dfrac{1}{3}.\dfrac{1}{2}BD = \dfrac{1}{6}.a\sqrt 2 \) Kẻ \(PQ||SA \Rightarrow PQ = \dfrac{1}{3}SA = \dfrac{{2a}}{3}\) \(\begin{array}{l}CQ = \dfrac{1}{3}MA + 3MA = \dfrac{{10}}{3}.MA\\ = \dfrac{{10}}{3}.\dfrac{1}{4}AC = \dfrac{5}{6}AC = \dfrac{{5.a\sqrt 2 }}{6}\\ \Rightarrow CP = \sqrt {C{Q^2} + P{Q^2}} \\ = \sqrt {\dfrac{{25{a^2}}}{{18}} + \dfrac{{4{a^2}}}{9}} = a\sqrt {\dfrac{{11}}{6}} \\ \Rightarrow CG = \sqrt {C{P^2} + G{P^2}} = \dfrac{{a\sqrt {17} }}{3}\\ \Rightarrow \sin \alpha = \dfrac{{GP}}{{CG}} = \dfrac{{\sqrt 2 }}{6}.\dfrac{3}{{\sqrt {17} }} = \dfrac{1}{{\sqrt {34} }}\end{array}\)
|