Giải đề thi học kì 2 toán lớp 11 năm 2020 - 2021 trường THPT Đoàn ThượngLàm bàiCâu hỏi 1 : Cho hình lập phương \(ABCD.A’B’C’D’\). Khoảng cách từ điểm B đến mặt phẳng \(A’B’C’D’\) là
Đáp án: C Phương pháp giải: Xác định qua B và vuông góc với \(\left( {A'B'C'D'} \right)\). Lời giải chi tiết: \(BB' \bot \left( {A'B'C'D'} \right)\) nên \(BB' = d\left( {B,\left( {A'B'C'D'} \right)} \right)\) Câu hỏi 2 : Cho hàm số \(f\left( x \right) = 3{x^3}\). Giá trị của \(f''\left( 1 \right)\) bằng
Đáp án: C Phương pháp giải: Tính \(f'\left( x \right),f''\left( x \right) = \left[ {f'\left( x \right)} \right]'\). Thay x=1 vào . Lời giải chi tiết: Câu hỏi 3 : \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x}\) bằng
Đáp án: D Phương pháp giải: Lý thuyết giới hạn. Lời giải chi tiết: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1\) Câu hỏi 4 : Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và tam giác SAC vuông cân tại A. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng
Đáp án: D Phương pháp giải: Tìm hình chiếu của SC lên (ABC). Góc giữa SC và (ABC) là góc giữa SC và hình chiếu. Lời giải chi tiết: Hình chiếu của SC lên (ABC) là AC. => Góc giữa SC và \(\left( {ABC} \right)\) là góc giữa SC và AC và bằng \(\widehat {SCA}\). Tam giác SAC vuông cân tại A nên \(\widehat {SCA} = 45^\circ \). Câu hỏi 5 : Cho hai hàm số \(f\left( x \right)\) và \(g\left( x \right)\) có \(f'\left( 2 \right) = 1,g'\left( 2 \right) = 4\). Đạo hàm của hàm số \(f\left( x \right) - g\left( x \right)\) tại điểm \(x = 2\) bằng
Đáp án: D Phương pháp giải: \(\left[ {g\left( x \right) - f\left( x \right)} \right]' = g'\left( x \right) - f'\left( x \right)\) Lời giải chi tiết: \(\left[ {g\left( x \right) - f\left( x \right)} \right]{'_{x = 2}} = g'\left( 2 \right) - f'\left( 2 \right) = 3\) Câu hỏi 6 : Đạo hàm của hàm số \(y = \sqrt x \left( {x > 0} \right)\) là
Đáp án: C Phương pháp giải: Công thức đạo hàm cơ bản. Lời giải chi tiết: \(y' = \left( {\sqrt x } \right)' = \dfrac{1}{{2\sqrt x }}\) Câu hỏi 7 : Đạo hàm của hàm số \(y = 2x - \sqrt x \) là
Đáp án: B Phương pháp giải: \(y' = \left( {\sqrt x } \right)' = \dfrac{1}{{2\sqrt x }}\), \(\left( {kx} \right)' = k\) với k là hằng số. Lời giải chi tiết: \(y' = 2 - \dfrac{1}{{2\sqrt x }}\) Câu hỏi 8 : Giá trị của \(\lim \dfrac{{3{n^2} + 2}}{{{{\left( {2n - 1} \right)}^2}}}\) bằng
Đáp án: C Phương pháp giải: Chia cả tử và mẫu cho \({n^2}\). Sử dụng kết quả \(\lim \dfrac{1}{n} = \lim \dfrac{1}{{{n^2}}} = 0\) Lời giải chi tiết: \(\lim \dfrac{{3{n^2} + 2}}{{{{\left( {2n - 1} \right)}^2}}} = \lim \dfrac{{3 + \dfrac{2}{{{n^2}}}}}{{4 - \dfrac{4}{n} + \dfrac{1}{{{n^2}}}}} = \dfrac{3}{4}\) Câu hỏi 9 : Hàm số nào dưới đây liên tục tại \(x = - 1\)?
Đáp án: D Phương pháp giải: Hàm đa thức luôn liên tục trên \(\mathbb{R}\) Lời giải chi tiết: Hàm số \(f\left( x \right) = 3x + 3\) liên tục trên \(\mathbb{R}\) nên liên tục tại x= -1. Câu hỏi 10 : Cho hình lăng trụ đứng \(ABC.A'B'C'\). Khẳng định nào sau đây đúng?
Đáp án: B Phương pháp giải: Hình lăng trụ đứng có cạnh bên vuông góc với đáy. Lời giải chi tiết: BB’ là cạnh bên của ABC.A’B’C’ nên \(BB' \bot \left( {ABC} \right)\) Câu hỏi 11 : Cho hàm số \(f\left( x \right)\) có \(f'\left( 1 \right) = 2\). Đạo hàm của hàm số \(3f\left( x \right)\) tại điểm x=1 bằng
Đáp án: C Phương pháp giải: \(\left[ {k.f\left( x \right)} \right]' = k.f'\left( x \right)\). Thay x=1 Lời giải chi tiết: \(g\left( x \right) = 3f\left( x \right) \Rightarrow g'\left( x \right) = 3.f'\left( x \right)\). Thay x=1 vào ta được: \(g'\left( 1 \right) = 3.f'\left( 1 \right) = 6\) Câu hỏi 12 : \(\mathop {\lim }\limits_{x \to 1} \left( {{x^3} - 1} \right)\) bằng
Đáp án: D Phương pháp giải: Thay x=1 vào biểu thức \({x^3} - 1\). Lời giải chi tiết: \(\mathop {\lim }\limits_{x \to 1} \left( {{x^3} - 1} \right) = {1^3} - 1 = 0\) Câu hỏi 13 : Cho f là hàm số liên tục tại \({x_0}\). Đạo hàm của f tại \({x_0}\) là:
Đáp án: C Phương pháp giải: Định nghĩa đạo hàm. Lời giải chi tiết: \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) nếu tồn tại giới hạn này. Câu hỏi 14 : Đạo hàm cấp hai của hàm số \(y = {x^2} + x\) là
Đáp án: A Phương pháp giải: Sử dụng các quy tắc tính đạo hàm cơ bản. Tính \(y',\)\(y'' = \left( {y'} \right)'\). Lời giải chi tiết: \(y' = 2x + 1 = > y'' = 2\) Câu hỏi 15 : Giá trị của \(\lim {\left( {\dfrac{\pi }{2}} \right)^n}\) bằng:
Đáp án: D Phương pháp giải: \(q > 1 \Rightarrow \lim {q^n} = + \infty \) Lời giải chi tiết: Ta có \(\dfrac{\pi }{2} > 1 \Rightarrow \lim {\left( {\dfrac{\pi }{2}} \right)^n} = + \infty \) Câu hỏi 16 : Cho hai dãy số \(\left( {{u_n}} \right),\left( {{v_n}} \right)\) thỏa mãn \(\lim {u_n} = - 1,\lim {v_n} = + \infty \). Giá trị của \(\lim \dfrac{{{u_n}}}{{{v_n}}}\) bằng
Đáp án: A Phương pháp giải: \(\lim {u_n} = L,\lim {v_n} = + \infty \Rightarrow \lim \dfrac{{{u_n}}}{{{v_n}}} = 0\) Lời giải chi tiết: \(\lim \dfrac{{{u_n}}}{{{v_n}}} = 0\) Câu hỏi 17 : Đạo hàm của hàm số \(y = \cot 2x\) là
Đáp án: A Phương pháp giải: Sử dụng công thức: \(\left( {\cot ax} \right)' = \dfrac{{ - a}}{{{{\sin }^2}ax}}\) Lời giải chi tiết: \(\left( {\cot 2x} \right)' = \dfrac{{ - 2}}{{{{\sin }^2}ax}}\) Câu hỏi 18 : Tiếp tuyến của đồ thị hàm số \(y = {x^3} - 2x\) tại điểm \(M\left( {1; - 1} \right)\) có hệ số góc bằng
Đáp án: C Phương pháp giải: \(y'\left( {{x_0}} \right)\) là hệ số góc của tiếp tuyến tại \(x = {x_0}\). Tìm \(y'\). Thay x=1 vào y’. Lời giải chi tiết: \(y' = 3{x^2} - 2 \Rightarrow y'\left( 1 \right) = 1\) Câu hỏi 19 : Trong không gian, cho tam giác ABC. Vecto \(\overrightarrow {CB} + \overrightarrow {AC} \) bằng
Đáp án: C Phương pháp giải: Quy tắc tam giác. Lời giải chi tiết: \(\overrightarrow {CB} + \overrightarrow {AC} = \overrightarrow {AB} \) Câu hỏi 20 : Hình chóp S.ABC có ABC là tam giác vuông tại C và \(SA \bot \left( {ABC} \right)\). Mệnh đề nào dưới dây đúng?
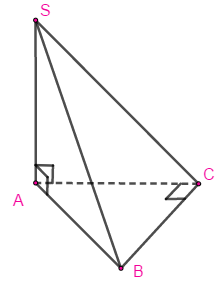
Đáp án: C Phương pháp giải: Tìm mặt phẳng chứa 2 đường thẳng vuông góc với BC. Lời giải chi tiết:
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\) \(\Delta ABC\) vuông tại C nên \(BC \bot AC\). => \(BC \bot \left( {SAC} \right)\) Câu hỏi 21 : Trong không gian cho hai vecto \(\overrightarrow u ,\overrightarrow v \) tạo với nhau một góc \(60^\circ \), \(\left| {\overrightarrow u } \right| = 1\) và \(\left| {\overrightarrow v } \right| = 2\). Tích vô hướng \(\overrightarrow u .\overrightarrow v \) bằng
Đáp án: A Phương pháp giải: \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\overrightarrow v } \right)\) Lời giải chi tiết: \(\overrightarrow u .\overrightarrow v = 1.2.\cos 60^\circ = 1\) Câu hỏi 22 : Khẳng định nào sau đây là SAI?
Đáp án: B Phương pháp giải: Lý thuyết góc giữa 2 đường thẳng: Góc giữa hai đường thẳng trong không gian luôn lớn hơn hoặc bằng \(0^\circ \) và nhỏ hơn hoặc bằng \(90^\circ \) Lời giải chi tiết: Đáp án B sai vì: Góc giữa a và b không được quá \(90^\circ \) Câu hỏi 23 : Đạo hàm của hàm số \(y = \cos 3x\) tại \(x = \dfrac{\pi }{2}\) là
Đáp án: A Phương pháp giải: Đạo hàm của hàm lượng giác: \(\left( {\cos ax} \right)' = - a.\sin ax\). Thay \(x = \dfrac{\pi }{2}\) vào đạo hàm. Lời giải chi tiết: \(\left( {\cos 3x} \right)' = - 3\sin 3x\) \( \Rightarrow y'\left( {\dfrac{\pi }{2}} \right) = - 3.\sin \left( {\dfrac{{3.\pi }}{2}} \right) = 3\) Câu hỏi 24 : Đạo hàm của hàm số \(y= cosx\) là Phương pháp giải: Công thức đạo hàm của cosx. Lời giải chi tiết: \(\left( {\cos x} \right)' = - \sin x\) Câu hỏi 25 : Đạo hàm của hàm số \(y = \cos x - \sin x\) là
Đáp án: A Phương pháp giải: \(\begin{array}{l}\left[ {f\left( x \right) - g\left( x \right)} \right]' = f'\left( x \right) - g'\left( x \right)\\\left( {\cos x} \right)' = - \sin x;\left( {\sin x} \right)' = \cos x\end{array}\) Lời giải chi tiết: \(\begin{array}{l}y' = \left( {\cos x - \sin x} \right)'\\ = \left( {\cos x} \right)' - \left( {\sin x} \right)'\\ = - \sin x - \cos x\end{array}\) Câu hỏi 26 : Đạo hàm của hàm số \(y = {x^2} - 2\cos x\) là
Đáp án: D Phương pháp giải: \(\begin{array}{l}\left[ {f\left( x \right) - g\left( x \right)} \right]' = f'\left( x \right) - g'\left( x \right)\\\left( {\cos x} \right)' = - \sin x;\left( {{x^n}} \right)' = n.{x^{n - 1}}\end{array}\) Lời giải chi tiết: \(y' = 2x + 2\sin x\) Câu hỏi 27 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O có đường chéo \(AC = BD = 2a\), \(SO \bot \left( {ABCD} \right),SO = OB\). Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng
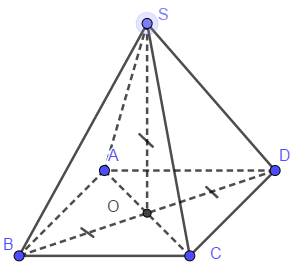
Đáp án: C Phương pháp giải: Tính SO. Lời giải chi tiết:
\(SO \bot \left( {ABCD} \right),SO = OB\) nên \(SO = d\left( {S,\left( {ABCD} \right)} \right)\) và \(SO = OB = \dfrac{{BD}}{2} = a\) Câu hỏi 28 : Khẳng định nào sau đây là đúng?
Đáp án: B Phương pháp giải: + Có duy nhất 1 mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước. + Đường thẳng vuông góc với 2 đường thẳng phân biệt cắt nhau trong 1 mặt phẳng thì vuông góc với mặt phẳng đó. Lời giải chi tiết: Đáp án B đúng vì: 2 cạnh của một tam giác phân biệt và cắt nhau trong mặt phẳng chứa tam giác đó. Khi đó đường thẳng vuông góc với 2 cạnh này thì vuông góc với mặt phẳng chứa 2 cạnh và vuông với cạnh còn lại. Câu hỏi 29 : Cho hàm số \(f\left( x \right) = \dfrac{1}{x}\left( {x \ne 0} \right)\). Khi đó \(f'\left( x \right)\) bằng
Đáp án: C Phương pháp giải: Công thức đạo hàm cơ bản. Lời giải chi tiết: \(f'\left( x \right) = - \dfrac{1}{{{x^2}}}\) Câu hỏi 30 : \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{{x^2} + 1}}{{x - 2}}\) bằng
Đáp án: A Phương pháp giải: Tách \({x^2}\) và x ra khỏi tử và mẫu. Lời giải chi tiết: \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{{x^2} + 1}}{{x - 2}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{{x^2}\left( {1 + \dfrac{1}{{{x^2}}}} \right)}}{{x\left( {1 - \dfrac{2}{x}} \right)}}\)\( = \mathop {\lim }\limits_{x \to + \infty } x = + \infty \) Câu hỏi 31 : Đạo hàm của hàm số \(y = 2{x^3}\) tại điểm x=2 bằng
Đáp án: A Phương pháp giải: \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\) Lời giải chi tiết: \(y' = 6{x^2} \Rightarrow y'\left( 2 \right) = 24\) Câu hỏi 32 : Đạo hàm của hàm số \(y=(2x+1)^2\) là
Đáp án: B Phương pháp giải: \(\left( {{u^n}} \right)' = n.{u^{n - 1}}.u'\) Lời giải chi tiết: \(y' = \left[ {{{\left( {2x + 1} \right)}^2}} \right]' = 2.\left( {2x + 1} \right).2\)\( = 4\left( {2x + 1} \right)\) Câu hỏi 33 : Cho \(\left( {{u_n}} \right)\) là cấp số nhân lùi vô hạn với \({u_1} = 3\) và công bội \(q = \dfrac{1}{2}\). Tổng của \(\left( {{u_n}} \right)\) bằng:
Đáp án: B Phương pháp giải: Tổng cấp số nhân lùi vô hạn: \(S = \dfrac{{{u_1}}}{{1 - q}}\) Lời giải chi tiết: \(S = \dfrac{3}{{1 - \dfrac{1}{2}}} = 6\) Câu hỏi 34 : Đạo hàm của hàm số \(y=(x+1)x\) là
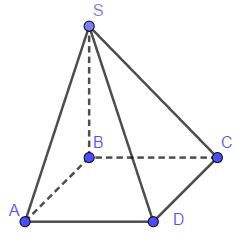
Đáp án: B Phương pháp giải: \(\left( {u.v} \right)' = u'.v - v'.u\) Lời giải chi tiết: \(y' = x + x + 1 = 2x + 1\) Câu hỏi 35 : Cho hình chóp S.ABCD có SB vuông góc với mặt phẳng (ABCD). Mặt phẳng (ABCD) vuông góc với mặt phẳng nào dưới đây?
Đáp án: C Phương pháp giải: Mặt phẳng (P) chứa đường thẳng vuông góc với (Q) thì (P) vuông góc với (Q). Lời giải chi tiết:
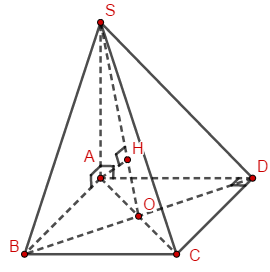
\(SB \bot \left( {ABCD} \right) \Rightarrow \left( {SAB} \right) \bot \left( {ABCD} \right)\) Câu hỏi 36 : Tính đạo hàm của hàm số \(y = f\left( x \right) = {x^4} - 2\sqrt x \) Phương pháp giải: \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\), \(\left( {\sqrt x } \right)' = \dfrac{1}{{2\sqrt x }}\) Lời giải chi tiết: \(y' = \left( {{x^4} - 2\sqrt x } \right)' = 4{x^3} - 2.\dfrac{1}{{2\sqrt x }}\)\( = 4{x^3} - \dfrac{1}{{\sqrt x }}\) Câu hỏi 37 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA vuông góc với đáy, H là hình chiếu của A lên SO. Chứng minh đường thẳng AH vuông góc với (SBD). Phương pháp giải: + Chứng minh \(BD \bot AH\). + Đường thẳng vuông góc với 2 đường thẳng phân biệt cắt nhau trong 1 mặt phẳng thì vuông góc với mặt phẳng đó. Lời giải chi tiết:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\\BD \bot AC\end{array} \right\}\\ \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} \Rightarrow BD \bot AH \subset \left( {SAC} \right)\\AH \bot SO\end{array} \right\}\\ \Rightarrow AH \bot \left( {SBD} \right)\end{array}\) Câu hỏi 38 :
Câu 1: Cho a và b là các số thực khác 0. Biết \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} + bx + 2} - 2ax} \right) = 4\). Tìm a+b. Phương pháp giải: Nhân liên hợp. Chia cả tử và mẫu cho x. Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} + bx + 2} - 2ax} \right)\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{4{x^2} + bx + 2 - 4{a^2}{x^2}}}{{\sqrt {4{x^2} + bx + 2} + 2ax}}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{4{x^2} + bx + 2 - 4{a^2}{x^2}}}{{\sqrt {4{x^2} + bx + 2} + 2ax}}\end{array}\) Để giới hạn trên bằng 4 thì bậc của tử và mẫu phải bằng nhau. Tức là không còn \({x^2}\). Do đó \({a^2} = 1\). Vì \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} + bx + 2} - 2ax} \right) = 4\) nên a > 0 (vì nếu a< 0 thì giới hạn trên bằng vô cùng). Do đó a=1. \(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \dfrac{{4{x^2} + bx + 2 - 4{a^2}{x^2}}}{{\sqrt {4{x^2} + bx + 2} + 2ax}}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{bx + 2}}{{\sqrt {4{x^2} + bx + 2} + 2ax}}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x\left( {b + \dfrac{2}{x}} \right)}}{{x\left( {\sqrt {4 + \dfrac{b}{x} + \dfrac{2}{{{x^2}}}} + 2a} \right)}}\\ = \dfrac{b}{{2 + 2a}} = 4\\ \Leftrightarrow b = 8 + 8a = 16 \Rightarrow a + b = 17\end{array}\) Câu 2: Cho hàm số \(y = - {x^3} + 3x + 2\) có đồ thị là (C). Tìm những điểm trên trục hoành sao cho từ đó kẻ được 3 tiếp tuyến đến đồ thị hàm số và trong đó có hai tiếp tuyến vuông góc với nhau. Phương pháp giải: Gọi điểm trên hoành độ là \(A\left( {a;0} \right)\). Tính y’. Lời giải chi tiết: Gọi điểm trên hoành độ là \(A\left( {a;0} \right)\). \(y' = - 3{x^2} + 3\). Gọi \({x_0}\) là hoành độ tiếp điểm của tiếp tuyến. \( \Rightarrow f'\left( {{x_0}} \right) = \left( {{x_0} + 1} \right)\left( {3 - 3{x_0}} \right)\). Khi đó tiếp tuyến tại \(\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là: \(y = \left( {{x_0} + 1} \right)\left( {3 - 3{x_0}} \right).\left( {x - {x_0}} \right) - {\left( {{x_0} + 1} \right)^2}\left( {{x_0} - 2} \right)\) Vì tiếp tuyến đi qua điểm \(A\left( {a;0} \right)\) nên phương trình: \(0 = \left( {{x_0} + 1} \right)\left( {3 - 3{x_0}} \right).\left( {a - {x_0}} \right) - {\left( {{x_0} + 1} \right)^2}\left( {{x_0} - 2} \right)\) luôn có 3 nghiệm phân biệt. \( \Rightarrow {x_0} = 1 \Rightarrow f'\left( {{x_0}} \right) = 0 = f\left( {{x_0}} \right)\)
|