Lời giải chi tiết:

Tâm I thuộc mặt phẳng \(\left( {xOy} \right):{\text{ }}z = 0\)  nên ta có \(z = 0\) . Suy ra, giả sử \(I\left( {x,y,0} \right)\).

Mặt cầu \(\left( S \right)\)  qua \(A,{\text{ }}B,{\text{ }}C\) nên ta có \(IA = IB = IC = R\)

Ta có

\(\left\{ {\begin{array}{*{20}{l}}{I{A^2} = I{B^2}}&{}\\{I{B^2} = I{C^2}}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{(x - 1)}^2} + {{(y - 2)}^2} + {{(4)}^2} = {{(x - 1)}^2} + {{(y + 3)}^2} + {{( - 1)}^2}}&{}\\{{{(x - 1)}^2} + {{(y + 3)}^2} + {{( - 1)}^2} = {{(x - 2)}^2} + {{(y - 2)}^2} + {{(3)}^2}}&{}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 4y + 4 + 16 = 6y + 9 + 1}&{}\\{ - 2x + 1 + 6y + 9 + 1 = - 4x + 4 - 4y + 4 + 9}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 10y = - 10}&{}\\{2x + 10y = 6}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 1}&{}\\{x = - 2}&{}\end{array}} \right.\)

Vậy \(I\left( { - 2,1,0} \right)\).

Có \(IA = \sqrt {26}  = R\)

Chọn B

Phương pháp giải:

Gọi phương trình mặt cầu có dạng \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}+2ax+2by+2cz+d=0\,\,\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-d>0 \right)\)

Thay tọa độ các điểm M, N, P, Q vào phương trình mặt cầu, suy ra hệ bốn phương trình bốn ẩn a, b, c, d. Giải hệ phương trình và suy ra tọa độ tâm \(I\left( -a;-b;-c \right)\) của mặt cầu.

Lời giải chi tiết:

Gọi phương trình mặt cầu có dạng \(\left( S \right):\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+2ax+2by+2cz+d=0\,\,\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-d>0 \right)\)

Vì \(M,N,P,Q\in \left( S \right)\Rightarrow \) ta có hệ phương trình

\(\left\{ \begin{array}{l}{2^2} + {2^2} + {2^2} + 4a + 4b + 4c + d = 0\,\,\\{4^2} + {0^2} + {2^2} + 8a + 4c + d = 0\,\,\\{4^2} + {2^2} + {0^2} + 8a + 4b + d = 0\,\,\\{4^2} + {2^2} + {2^2} + 8a + 4b + 4c + d = 0\,\,\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 3\\b =  - 1\\c =  - 1\\d = 8\end{array} \right. \Rightarrow I\left( {3;1;1} \right)\) là tâm của mặt cầu.

Chọn B.

Phương pháp giải:

Bán kính của mặt cầu bằng khoảng cách từ tâm I đến mặt phẳng (Oyz).

Lời giải chi tiết:

Vì (S) tiếp xúc với mặt phẳng (Oyz) nên bán kính của mặt cầu \(R=\left| {{x}_{I}} \right|=2\)

Vậy phương trình mặt cầu là: \({{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=4\)

Chọn C.

Phương pháp giải:

\({{d}^{2}}+{{r}^{2}}={{R}^{2}}\)

Trong đó,

\(d\): khoảng cách từ tâm O đến mặt phẳng (P),

\(r\): bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P),

\(R\): bán kính hình cầu.

Lời giải chi tiết:

\((S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y-2z+5=0\Leftrightarrow {{(x-3)}^{2}}+{{(y+2)}^{2}}+{{(z-1)}^{2}}=9\)

\(\Rightarrow \left( S \right)\) có tâm \(I(3;-2;1)\), bán kính \(R=3\).

\((Q)\) cắt \((S)\) theo giao tuyến là một đường tròn bán kính \(r=2\)

Ta có:  \({{d}^{2}}+{{r}^{2}}={{R}^{2}}\Leftrightarrow {{d}^{2}}+{{2}^{2}}={{3}^{2}}\Leftrightarrow d=\sqrt{5}\)

Gọi \(\overrightarrow{n}(a;b;c),\,\,\,\left( \overrightarrow{n}\ne \overrightarrow{0} \right)\) là một VTPT của (Q). Khi đó \(\overrightarrow{n}\) vuông góc với VTCP \(\overrightarrow{u}(1;0;0)\)của Ox  \(\Rightarrow 1.a+0.b+0.c=0\Leftrightarrow a=0\)

Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT \(\overrightarrow{n}(0;b;c),\,\,\,\left( \overrightarrow{n}\ne \overrightarrow{0} \right)\) là:

\(0.(x-0)+b(y-0)+c(z-0)=0\Leftrightarrow by+cz=0\)

Khoảng cách từ tâm I đến (Q):

\(d=\frac{\left| b.(-2)+c.1 \right|}{\sqrt{{{b}^{2}}+{{c}^{2}}}}=\sqrt{5}\Rightarrow {{\left( 2b-c \right)}^{2}}=5({{b}^{2}}+{{c}^{2}})\Leftrightarrow {{b}^{2}}+4bc+4{{c}^{2}}=0\Leftrightarrow {{(b+2c)}^{2}}=0\Leftrightarrow b=-2c\)

Cho \(c=-1\Rightarrow b=2\Rightarrow \overrightarrow{n}(0;2;-1)\). Phương trình mặt phẳng (Q): \(2y-z=0\).

Chọn: D

Phương pháp giải:

 Chứng minh khoảng cách từ O đến (ABC) không đổi. 

Lời giải chi tiết:

Kẻ \(OH\bot AB\,\,\left( H\in AB \right);\,\,OK\bot Ch\,\,\left( K\in CH \right)\) ta có

\(\begin{array}{l}
\left\{ \begin{array}{l}
AB \bot OH\\
AB \bot OC
\end{array} \right. \Rightarrow AB \bot \left( {OHC} \right) \Rightarrow AB \bot OK\\
\left\{ \begin{array}{l}
OK \bot AB\\
OK \bot CH
\end{array} \right. \Rightarrow OK \bot \left( {ABC} \right)
\end{array}\)

Ta sẽ chứng minh OK không đổi, khi đó mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính OK.

Gọi \(A\left( a;0;0 \right);\,\,B\left( 0;b;0 \right);\,\,C\left( 0;0;c \right)\) ta có \({{V}_{ABC}}=\frac{1}{6}abc\). \(\begin{align} & \overrightarrow{AB}=\left( -a;b;0 \right);\,\,\overrightarrow{AC}=\left( -a;0;c \right)\Rightarrow \left[ \overrightarrow{AB};\overrightarrow{AC} \right]=\left( bc;ac;ab \right)\Rightarrow {{S}_{ABC}}=\frac{1}{2}\sqrt{{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}} \\ & \Rightarrow \frac{{{S}_{ABC}}}{{{V}_{OABC}}}=\frac{\frac{1}{2}\sqrt{{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}}}{\frac{1}{6}abc}=\frac{3}{2} \\ & \Leftrightarrow \sqrt{{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}}=\frac{1}{2}abc \\ & \Leftrightarrow {{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}=\frac{1}{4}{{a}^{2}}{{b}^{2}}{{c}^{2}} \\ & \Leftrightarrow \frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}=\frac{1}{4} \\ \end{align}\)

Xét tam giác vuông OCK có \(\frac{1}{O{{K}^{2}}}=\frac{1}{O{{C}^{2}}}+\frac{1}{O{{H}^{2}}}=\frac{1}{O{{C}^{2}}}+\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}=\frac{1}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}+\frac{1}{{{z}^{2}}}=\frac{1}{4}\Rightarrow OK=2\)

Vậy mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính 2.

Chọn B.

Phương pháp giải:

- Gọi \(M\left( {x;y;z} \right)\).

- Tính lần lượt các độ dài đoạn \(M{A^2};M{B^2}\) , sử dụng công thức \(M{A^2} = {\left( {{x_M} - {x_A}} \right)^2} + {\left( {{y_M} - {y_A}} \right)^2} + {\left( {{z_M} - {z_A}} \right)^2}\).

- Biểu thức tìm được có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\), là phương trình mặt cầu có tâm \(I\left( {a;b;c} \right)\), bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).

Lời giải chi tiết:

Gọi \(M\left( {x;y;z} \right)\).

Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,2M{A^2} + M{B^2} = 165\\ \Leftrightarrow 2\left[ {{{\left( {x - 1} \right)}^2} + {{\left( {y - 2} \right)}^2} + {{\left( {z - 3} \right)}^2}} \right] + \left[ {{{\left( {x - 4} \right)}^2} + {{\left( {y + 7} \right)}^2} + {{\left( {z + 9} \right)}^2}} \right] = 165\\ \Leftrightarrow 3{x^2} + 3{y^2} + 3{z^2} - 12x + 6y + 6z + 9 = 0\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 4x + 2y + 2z + 3 = 0\end{array}\)

Do đó tập hợp các điểm \(M\) thỏa mãn yêu cầu bài toán là mặt cầu tâm \(I\left( {2; - 1; - 1} \right)\) \( \Rightarrow a = 2,\,\,b =  - 1,\,\,c =  - 1\) , bán kính \(R = \sqrt {4 + 1 + 1 - 3}  = \sqrt 3 \).

Vậy \(T = {a^2} + {b^2} + {c^2} + {R^2} = 4 + 1 + 1 + 3 = 9\).

Chọn A.

Phương pháp giải:

- Áp dụng công thức tính khoảng cách hai điểm trong không gian.

- Thay các khoảng cách vào giả thiết rồi đưa phương trình về phương trình mặt cầu.

Lời giải chi tiết:

Ta có \(A\left( {1;0;0} \right),B\left( {2;3;0} \right),C\left( {0;0;3} \right);M\left( {x;y;z} \right)\)

\( \Rightarrow \left\{ \begin{array}{l}M{A^2} = {\left( {x - 1} \right)^2} + {y^2} + {z^2}\\M{B^2} = {\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {z^2}\\M{C^2} = {x^2} + {y^2}{\left( {z - 3} \right)^2}\end{array} \right.\)

\(\begin{array}{l} \Rightarrow M{A^2} + M{B^2} + M{C^2} = 23\\ \Rightarrow {\left( {x - 1} \right)^2} + {y^2} + {z^2} + {\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} + {x^2} + {y^2} + {\left( {z - 3} \right)^2} = 23\\ \Leftrightarrow 3\left( {{x^2} + {y^2} + {z^2}} \right) - 6x - 6y - 6z = 0\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 2\left( {x + y + z} \right) = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 3\end{array}\)

\( \Rightarrow R = \sqrt 3 \)

Chọn C.

Phương pháp giải:

- Tham số hóa tọa độ điểm \(I \in \Delta \) theo tham số \(t\).

- Tính khoảng cách từ \(I\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,\,Ax + By + Cz + D = 0\): \(d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)

- Tính độ dài đoạn thẳng \(IH\): \(IH = \sqrt {{{\left( {{x_H} - {x_I}} \right)}^2} + {{\left( {{y_H} - {y_I}} \right)}^2} + {{\left( {{z_H} - {z_I}} \right)}^2}} \) .

- Giải phương trình \(d\left( {I;\left( P \right)} \right) = IH = R\) tìm \(t\), từ đó suy ra tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu \(\left( S \right)\).

- Mặt cầu tâm \(I\left( {{x_0};{y_0};{z_0}} \right)\), bán kính \(R\) có phương trình \({\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {R^2}\).

Lời giải chi tiết:

Vì \(I \in \Delta :\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) nên ta gọi \(I\left( {1 - 2t;\,\,2t;\,\,2 + t} \right)\).

Vì \(\left( S \right)\) tiếp xúc với \(\left( P \right):\,\,2x - y + z - 3 = 0\) tại điểm \(H\left( {1; - 1;0} \right)\) nên ta có: \(d\left( {I;\left( P \right)} \right) = IH = R\).

\(\begin{array}{l} \Leftrightarrow \dfrac{{\left| {2.\left( {1 - 2t} \right) - 2t + 2 + t - 3} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \sqrt {{{\left( {2t} \right)}^2} + {{\left( { - 1 - 2t} \right)}^2} + {{\left( { - 2 - t} \right)}^2}} \\ \Leftrightarrow \dfrac{{\left| { - 5t + 1} \right|}}{{\sqrt 6 }} = \sqrt {9{t^2} + 8t + 5} \\ \Leftrightarrow 25{t^2} - 10t + 1 = 54{t^2} + 48t + 30\\ \Leftrightarrow 29{t^2} + 58t + 29 = 0\\ \Leftrightarrow {t^2} + 2t + 1 = 0\\ \Leftrightarrow {\left( {t + 1} \right)^2} = 0\\ \Leftrightarrow t =  - 1\end{array}\)

\( \Rightarrow I\left( {3; - 2;1} \right)\) và \(R = IH = \sqrt 6 \).

Vậy phương trình mặt cầu \(\left( S \right)\) là: \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 6\).

Chọn C.

Phương pháp giải:

- Xét điểm \(I\left( {x;y;z} \right)\) thỏa mãn \(3\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 \). Tìm tọa độ điểm I.

- Phân tích đẳng thức đề bài cho bằng cách chèn điểm I. Từ đó tính được MI.

- Kết luận M thuộc mặt cầu tâm I, bán kính MI không đổi.

Lời giải chi tiết:

Xét điểm \(I\left( {x;y;z} \right)\) thỏa mãn \(3\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 \) \( \Leftrightarrow \left\{ \begin{array}{l}3\left( {2 - x} \right) + 2\left( {0 - x} \right) = 0\\3\left( {0 - y} \right) + 2\left( { - 6 - y} \right) = 0\\3\left( {4 - z} \right) + 2\left( {0 - z} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{6}{5}\\y =  - \dfrac{{12}}{5}\\z = \dfrac{{12}}{5}\end{array} \right.\).

\( \Rightarrow I\left( {\dfrac{6}{5}; - \dfrac{{12}}{5};\dfrac{{12}}{5}} \right)\).

Mà \(A{B^2} = {2^2} + {6^2} = {4^2} = 56\).

Xét

\(\begin{array}{l}\,\,\,\,\,\,3M{A^2} + 2M{B^2} = \dfrac{{561}}{5}\\ \Leftrightarrow 3{\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2} = \dfrac{{561}}{5}\\ \Leftrightarrow 3\left( {M{I^2} + 2\overrightarrow {MI} .\overrightarrow {IA}  + I{A^2}} \right) + 2\left( {M{I^2} + 2\overrightarrow {MI} .\overrightarrow {IB}  + I{B^2}} \right) = \dfrac{{561}}{5}\\ \Leftrightarrow 5M{I^2} + 2\overrightarrow {MI} \left( {3\overrightarrow {IA}  + 2\overrightarrow {IB} } \right) + 3I{A^2} + 2I{B^2} = \dfrac{{561}}{5}\\ \Leftrightarrow 5M{I^2} + \dfrac{{672}}{{25}} + \dfrac{{1008}}{{25}} = \dfrac{{561}}{5}\\ \Leftrightarrow M{I^2} = 9 \Leftrightarrow MI = 3.\end{array}\)

Vậy M luôn chạy trên mặt cầu tâm \(I\left( {\dfrac{6}{5}; - \dfrac{{12}}{5};\dfrac{{12}}{5}} \right)\), bán kính R = MI = 3.

Chọn A.

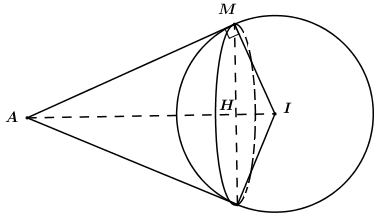
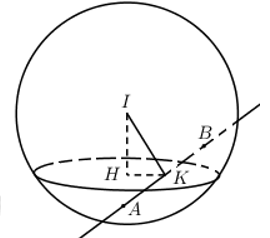
Phương pháp giải:

- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông.

Lời giải chi tiết:

Mặt cầu (S) có tâm I(1;0;4), bán kính R = 3.

Gọi H là giao điểm của IA là mặt phẳng chứa đường tròn là tập hợp các điểm M. Khi đó H là tâm đường tròn tập hợp tiếp điểm, bán kính r = HM.

Ta có: \(IA = \sqrt {{3^2} + {0^2} + {{\left( { - 3} \right)}^2}}  = 3\sqrt 2 \).

Áp dụng định lí Pytago trong tam giác vuong IAM có: \(AM = \sqrt {I{A^2} - I{M^2}}  = \sqrt {18 - 9}  = 3\).

Áp dụng hệ thức lượng trong tam giác vuông IAM có: \(MH = \dfrac{{IM.AM}}{{IA}} = \dfrac{{3.3}}{{3\sqrt 2 }} = \dfrac{{3\sqrt 2 }}{2}\).

Chọn B.

Phương pháp giải:

+) Viết phương trình mặt phẳng giao tuyến.

+) Tâm của đường tròn giao tuyến là giao điểm của \({I_1}{I_2}\) và mặt phẳng giao tuyến với \({I_1},\,\,{I_2}\) lần lượt là tâm của hai mặt cầu \(\left( {{S_1}} \right),\,\,\left( {{S_2}} \right)\).

Lời giải chi tiết:

Phương trình mặt phẳng giao tuyến của 2 mặt cầu là

\(\begin{array}{l}{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} - {\left( {x + 1} \right)^2} - {\left( {y - 2} \right)^2} - {\left( {z + 1} \right)^2} = 16 - 9\\ \Leftrightarrow  - 2x + 1 - 2y + 1 - 4z + 4 - 2x - 1 + 4y - 4 - 2z - 1 = 7\\ \Leftrightarrow  - 4x + 2y - 6z - 7 = 0 \Leftrightarrow 4x - 2y + 6z + 7 = 0\,\,\left( P \right)\end{array}\)

Mặt cầu \(\left( {{S_1}} \right)\) có tâm \({I_1}\left( {1;1;2} \right)\), bán kính \({R_1} = 4\).

Gọi \(\Delta \) là đường thẳng đi qua \({I_1}\) và vuông góc với \(\left( P \right) \Rightarrow \Delta :\,\,\dfrac{{x - 1}}{4} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{{z - 2}}{6}\).

Gọi \(I = \left( P \right) \cap \Delta  \Rightarrow I\left( {1 + 4t;1 - 2t;2 + 6t} \right)\).

\(I \in \left( P \right) \Rightarrow 4\left( {1 + 4t} \right) - 2\left( {1 - 2t} \right) + 6\left( {2 + 6t} \right) + 7 = 0 \Leftrightarrow 56t + 21 = 0 \Leftrightarrow t =  - \dfrac{3}{8}\).

\( \Rightarrow I\left( { - \dfrac{1}{2};\dfrac{7}{4}; - \dfrac{1}{4}} \right) \Rightarrow a + b + c =  - \dfrac{1}{2} + \dfrac{7}{4} - \dfrac{1}{4} = 1\).

Chọn D

Phương pháp giải:

Tính độ dài đoạn thẳng IM với I là tâm mặt cầu.

Tham số hóa tọa độ điểm M, sau đó dựa vào độ dài IM để tìm điểm M.

Lời giải chi tiết:

Mặt cầu (S) có tâm \(I\left( 1;2;-3 \right)\), bán kính \(R=3\sqrt{3}\)

Đặt \(MA=MB=MC=a\).

Tam giác \(MAB\) đều \(\Rightarrow AB=a\)

Tam giác \(MBC\) vuông tại M \(\Rightarrow BC=a\sqrt{2}\)

Tam giác \(MCA\) có \(\widehat{CMA}={{120}^{0}}\Rightarrow AC=a\sqrt{3}\)

Xét tam giác \(ABC\) có \(A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\Rightarrow \Delta ABC\) vuông tại B \(\Rightarrow \Delta ABC\) ngoại tiếp đường tròn nhỏ có đường kính \(AC\)\(\Rightarrow HA=\frac{1}{2}AC=\frac{a\sqrt{3}}{2}\)

Xét tam giác vuông \(IAM\) có:

\(\frac{1}{H{{A}^{2}}}=\frac{1}{A{{M}^{2}}}+\frac{1}{I{{A}^{2}}}\Rightarrow \frac{4}{3{{a}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{27}\Leftrightarrow \frac{1}{3{{a}^{2}}}=\frac{1}{27}\Leftrightarrow a=3=MA\)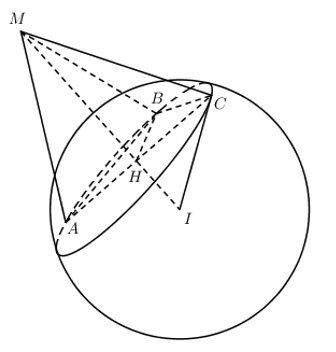

\(\Rightarrow I{{M}^{2}}=M{{A}^{2}}+I{{A}^{2}}={{3}^{2}}+27=36\)

\(\begin{array}{l}
M \in \left( d \right) \Rightarrow M\left( { - 1 + t; - 2 + t;1 + t} \right) \Leftrightarrow I{M^2} = {\left( {t - 2} \right)^2} + {\left( {t - 4} \right)^2} + {\left( {t + 4} \right)^2} = 36\\
\Leftrightarrow 3{t^2} - 4t = 0\\
\Leftrightarrow \left[ \begin{array}{l}
t = 0\\
t = \frac{4}{3}
\end{array} \right. \Rightarrow \left[ \begin{array}{l}
M\left( { - 1; - 2;1} \right)\\
M\left( {\frac{1}{3}; - \frac{2}{3};\frac{7}{3}} \right)\,\,\,\left( {ktm} \right)
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
a = - 1\\
b = - 2\\
c = 1
\end{array} \right. \Rightarrow a + b + c = - 2
\end{array}\)

Chọn B.

Phương pháp giải:

+) Gọi \(I\left( {a;b;c} \right)\) là điểm thỏa mãn \(\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 \), xác định tọa độ điểm \(I\).

+) Biến đổi biểu thức \(M{A^2} + 2M{B^2}\) bằng cách chèn điểm \(I\).

+) Tìm vị trí của \(M\) trên \(\left( S \right)\) để \(M{A^2} + 2M{B^2}\) đạt giá trị nhỏ nhất và tính.

Lời giải chi tiết:

Gọi \(I\left( {a;b;c} \right)\) là điểm thỏa mãn \(\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 \) ta có:

\(\begin{array}{l} \Rightarrow \left( { - a; - b;2 - c} \right) + 2\left( {1 - a;1 - b; - c} \right) = 0\\ \Leftrightarrow \left\{ \begin{array}{l} - a + 2 - 2a = 0\\ - b + 2 - 2b = 0\\2 - c - 2c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{3}\\b = \dfrac{2}{3}\\c = \dfrac{2}{3}\end{array} \right. \Rightarrow I\left( {\dfrac{2}{3};\dfrac{2}{3};\dfrac{2}{3}} \right)\end{array}\)

Ta có:

\(\begin{array}{l}M{A^2} + 2M{B^2} = {\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2}\\ = M{I^2} + 2\overrightarrow {MI} \overrightarrow {IA}  + I{A^2} + 2M{I^2} + 4\overrightarrow {MI} .\overrightarrow {IB}  + I{B^2}\\ = 3M{I^2} + I{A^2} + 2I{B^2} + 2\overrightarrow {MI} \underbrace {\left( {\overrightarrow {IA}  + 2\overrightarrow {IB} } \right)}_{\overrightarrow 0 } = 3M{I^2} + \underbrace {I{A^2} + 2I{B^2}}_{const}\end{array}\)

Do \(\left\{ \begin{array}{l}I{A^2} = {\left( {\dfrac{{ - 2}}{3}} \right)^2} + {\left( {\dfrac{{ - 2}}{3}} \right)^2} + {\left( {2 - \dfrac{2}{3}} \right)^2} = \dfrac{8}{3}\\I{B^2} = {\left( {1 - \dfrac{2}{3}} \right)^2} + {\left( {1 - \dfrac{2}{3}} \right)^2} + {\left( {\dfrac{{ - 2}}{3}} \right)^2} = \dfrac{2}{3}\end{array} \right. \Rightarrow I{A^2} + 2I{B^2} = 4\) không đổi \( \Rightarrow {\left( {M{A^2} + 2M{B^2}} \right)_{\min }} \Leftrightarrow M{I_{\min }}\) với \(I\left( {\dfrac{2}{3};\dfrac{2}{3};\dfrac{2}{3}} \right),\,\,M \in \left( S \right)\).

Ta có \({\left( {\dfrac{2}{3}} \right)^2} + {\left( {\dfrac{2}{3}} \right)^2} + {\left( {\dfrac{2}{3} - 1} \right)^2} = 1 > \dfrac{1}{4} \Rightarrow I\) nằm ngoài \(\left( S \right)\) .

Vậy \({\left( {M{A^2} + 2M{B^2}} \right)_{\min }} = 3MI_{\min }^2 + 4 = 3.{\left( {\dfrac{1}{2}} \right)^2} + 4 = \dfrac{{19}}{4}\).

Chọn D

Phương pháp giải:

- Gọi \(I\left( {a;b;c} \right)\) là tâm mặt cầu ngoại tiếp tứ diện \(OABC\) \( \Rightarrow IO = IA = IB = IC\).

- Giải hệ phương trình \(\left\{ \begin{array}{l}I{O^2} = I{A^2}\\I{O^2} = I{B^2}\\I{O^2} = I{C^2}\end{array} \right.\) tìm tọa độ điểm \(I\).

- Tính bán kính mặt cầu \(R = OI\).

- Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\).

Lời giải chi tiết:

Gọi \(I\left( {a;b;c} \right)\) là tâm mặt cầu ngoại tiếp tứ diện \(OABC\) \( \Rightarrow IO = IA = IB = IC\)\( \Rightarrow I{O^2} = I{A^2} = I{B^2} = I{C^2}\).

Khi đó ta có hệ phương trình:

\(\left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} = {\left( {x - 3} \right)^2} + {y^2} + {z^2}\\{x^2} + {y^2} + {z^2} = {x^2} + {\left( {y + 2} \right)^2} + {z^2}\\{x^2} + {y^2} + {z^2} = {x^2} + {y^2} + {\left( {z + 4} \right)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} = {\left( {x - 3} \right)^2}\\{y^2} = {\left( {y + 2} \right)^2}\\{z^2} = {\left( {z + 4} \right)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - 6x + 9 = 0\\4y + 4 = 0\\8z + 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{3}{2}\\y =  - 1\\z =  - 2\end{array} \right.\)

\( \Rightarrow I\left( {\dfrac{3}{2}; - 1;2} \right)\). Suy ra bán kính mặt cầu ngoại tiếp tứ diện \(OABC\) là \(R = IO = \sqrt {\dfrac{9}{4} + 1 + 4}  = \sqrt {\dfrac{{29}}{4}} \).

Váy diện tích cầu ngoại tiếp tứ diện \(OABC\) là \(S = 4\pi {R^2} = 4\pi .\dfrac{{29}}{4} = 29\pi .\)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

\(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 16\) có tâm \(I\left( {1; - 1;2} \right)\) và bán kính \(R = 4\)

Gọi M, N, P là các hình chiếu vuông góc của I lên 3 mặt phẳng;  \({r_1};{r_2};{r_3}\) là bán kính của đường tròn giao tuyến tương ứng.

Khi đó, A, I, P, N là 4 đỉnh của một hình hộp chữ nhật, ta có: \(I{M^2} + I{P^2} + I{N^2} = I{A^2} = {0^2} + {3^2} + {1^2} = 10\)

\( \Leftrightarrow {R^2} - r_1^2 + {R^2} - r_2^2 + {R^2} - r_3^2 = 10 \Leftrightarrow 3.16 - \left( {r_1^2 + r_2^2 + r_3^2} \right) = 10 \Leftrightarrow r_1^2 + r_2^2 + r_3^2 = 38\)

Tổng diện tích của ba hình tròn đó là: \(S = \pi \left( {r_1^2 + r_2^2 + r_3^2} \right) = 38\pi \).

Chọn: C.

Phương pháp giải:

- Tính \(IA = \sqrt {{{\left( {{x_A} - {x_I}} \right)}^2} + {{\left( {{y_A} - {y_I}} \right)}^2} + {{\left( {{z_A} - {z_I}} \right)}^2}} \) là độ dài bán kính mặt cầu.

- Mặt cầu tâm \(I\left( {a;b;c} \right)\) bán kính \(R\) là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).

Lời giải chi tiết:

Ta có \(I\left( {1; - 2;3} \right);\,\,A\left( { - 1;2;1} \right)\)\( \Rightarrow IA = \sqrt {{{\left( { - 2} \right)}^2} + {4^2} + {{\left( { - 2} \right)}^2}}  = \sqrt {24} .\)

Vì mặt cầu tâm \(I\) đi qua \(A\) nên bán kính của mặt cầu là \(R = IA = \sqrt {24} \).

Mặt cầu có tâm \(I\left( {1; - 2;3} \right);\,\,R = \sqrt {24} \) có phương trình là:

\({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 24\)\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 2x + 4y - 6z - 10 = 0.\)

Chọn C.

Phương pháp giải:

 Dựng hình, áp dụng công thức trung tuyến để biện luận giá trị lớn nhất 

Lời giải chi tiết:

Xét mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=9\) có tâm \(I\left( 1;2;2 \right),\) bán kính \(R=3.\)

Ta có \(MI=NI=3\sqrt{5}>3=R\)\(\Rightarrow \,\,M,\,\,N\) nằm bên ngoài khối cầu \(\left( S \right).\)

Gọi \(H\) là trung điểm của \(MN\)\(\Rightarrow \,\,H\left( 5;-\,2;4 \right)\) và \(E{{H}^{2}}=\frac{E{{M}^{2}}+E{{N}^{2}}}{2}-\frac{M{{N}^{2}}}{4}.\)

Lại có \({{\left( EM+EN \right)}^{2}}\le \left( {{1}^{2}}+{{1}^{2}} \right)\left( E{{M}^{2}}+E{{N}^{2}} \right)=2\left( E{{H}^{2}}+\frac{M{{N}^{2}}}{4} \right)\).

Để \({{\left\{ EM+EN \right\}}_{\max }}\Leftrightarrow E{{H}_{\max }}\)

Khi và chỉ khi \(E\) là giao điểm của \(IH\) và mặt cầu \(\left( S \right)\). Gọi \(\left( P \right)\) là mặt phẳng tiếp diện của \(\left( S \right)\) tại \(E\Rightarrow \,\,{{\vec{n}}_{\left( P \right)}}=a.\overrightarrow{EI}=b.\overrightarrow{IH}=b.\left( 4;-\,4;2 \right).\)

Dựa vào các đáp án ta thấy ở đáp án D, \({{\overrightarrow{n}}_{\left( P \right)}}=\left( 2;-2;1 \right)=\frac{1}{2}\left( 4;-4;2 \right)\)

Vậy phương trình mặt phẳng cần tìm là \(2x-2y+z+9=0.\)

Chọn D

Phương pháp giải:

Công thức khoảng cách từ điểm đến đường thẳng trong không gian:

      \(d\left( {A;\Delta } \right) = \dfrac{{\left| {\left[ {\overrightarrow u ;\overrightarrow {MA} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\) , với \(\overrightarrow u \) là VTCP của \(\Delta \) và M là điểm bất kì thuộc \(\Delta \).

Lời giải chi tiết:

Lấy \(M\left( {1; - 3;5} \right) \in d\)\( \Rightarrow \overrightarrow {MI} \left( {4;4; - 6} \right)\).

Đường thẳng d có 1 VTCP : \(\overrightarrow u \left( {2; - 1;3} \right)\)  \( \Rightarrow \left[ {\overrightarrow {MI} ;\overrightarrow u } \right] = \left( {6; - 24; - 12} \right)\)

\( \Rightarrow d\left( {I;d} \right) = \dfrac{{\left| {\left[ {\overrightarrow {MI} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \dfrac{{\sqrt {{6^2} + {{24}^2} + {{12}^2}} }}{{\sqrt {{2^2} + {1^2} + {3^2}} }} = \sqrt {54} \)

Mặt cầu có tâm \(I\left( {5;1; - 1} \right)\) và tiếp xúc với d có bán kính \(R = d\left( {I;d} \right) = \sqrt {54} \) có phương trình là:

\({\left( {x - 5} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 54\).

Chọn: B

Phương pháp giải:

Mặt cầu đường kính \(AB\) nhận trung điểm \(I\) của \(AB\) làm tâm và bán kính \(R = \dfrac{{AB}}{2}\)

Phương trình mặt cầu có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)

Lời giải chi tiết:

Trung điểm \(I\) của \(AB\) có tọa độ \(\left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_B}}}{2} = \dfrac{{7 + 1}}{2} = 4\\{y_I} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{ - 2 + 2}}{2} = 0\\{z_I} = \dfrac{{{z_A} + {z_B}}}{2} = \dfrac{{2 + 4}}{2} = 3\end{array} \right.\)  suy ra \(I\left( {4;0;3} \right)\)

\(AB = \sqrt {{{\left( {1 - 7} \right)}^2} + {{\left( {2 + 2} \right)}^2} + {{\left( {4 - 2} \right)}^2}}  = 2\sqrt {14} \)

Mặt cầu đường kính \(AB\) nhận trung điểm \(I\left( {4;0;3} \right)\) của \(AB\) làm tâm và bán kính \(R = \dfrac{{AB}}{2} = \sqrt {14} \)

Phương trình mặt cầu là \({\left( {x - 4} \right)^2} + {y^2} + {\left( {z - 3} \right)^2} = 14\) .

Chọn B

Phương pháp giải:

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm:

\({x^3} + 2{x^2} + mx - 3 = {x^2} + x - 1 \Leftrightarrow g\left( x \right) = {x^3} + {x^2} + \left( {m - 1} \right)x - 2 = 0\).

Đặt

\(\begin{array}{l}y = {x^2} + x - 1 \Rightarrow {y^2} = {\left( {{x^2} + x - 1} \right)^2}\\ = {x^4} + {x^2} + 1 + 2{x^3} - 2{x^2} - 2x = {x^4} + 2{x^3} - {x^2} - 2x + 1\end{array}\)

Chia \({y^2}\) cho \(g\left( x \right)\) ta được:

\(\begin{array}{l}{y^2} = g\left( x \right)\left( {x + 1} \right) - \left( {m + 1} \right){x^2} - \left( {m - 1} \right)x + 3\\ \Rightarrow {y^2} =  - m{x^2} - {x^2} - \left( {m - 1} \right)x + 3\\ \Leftrightarrow {x^2} + {y^2} + m\left( {y - x + 1} \right) + \left( {m - 1} \right)x - 3 = 0\\ \Leftrightarrow {x^2} + {y^2} - x + my + m - 3 = 0\,\,\,\left( C \right)\end{array}\)

\(\left( C \right)\) có bán kính bằng 3 (gt)

\(\begin{array}{l} \Rightarrow {\left( {\dfrac{1}{2}} \right)^2} + {\left( {\dfrac{m}{2}} \right)^2} - m + 3 = 9 \Leftrightarrow \dfrac{{{m^2}}}{4} - m - \dfrac{{23}}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 2 + 3\sqrt 3  \approx 7,2\\m = 2 - 3\sqrt 3  \approx  - 3,2\end{array} \right.\end{array}\)

Sử dụng MTCT thử lại \(m = 2 - 3\sqrt 3 \) thì phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Chọn B.

Sưu tầm: FB Strong Team Toán VD - VDC

Phương pháp giải:

Lời giải chi tiết:

\(IM = \sqrt {0 + {3^2} + {4^2}}  = 5 > r\)

Khi đó, \(AM \bot AI \Rightarrow \Delta AIM\) vuông tại A  \( \Rightarrow A\) di chuyển trên mặt cầu (S’) tâm J đường kính IM cố định.

Do đó, A di chuyển trên đường tròn giao tuyến (C) của mặt cầu (S) và mặt cầu (S’).

Dựng AH vuông góc IM tại H. Suy ra bán kính đường tròn (C) là : \(R = AH\).

Ta có: \(IH = \dfrac{{I{A^2}}}{{IM}} = \dfrac{{{4^2}}}{5} = \dfrac{{16}}{5} \Rightarrow HM = 5 - \dfrac{{16}}{5} = \dfrac{9}{5}\)

\( \Rightarrow AH = \sqrt {IH.HM}  = \sqrt {\dfrac{{16}}{5}.\dfrac{9}{5}}  = \dfrac{{12}}{5}\)

Vậy, các đường thẳng qua M  tiếp xúc với (S) tại các tiếp điểm thuộc đường tròn có bán kính \(R = \dfrac{{12}}{5}\).

Chọn: A

Phương pháp giải:

Mặt cầu tâm \(I\left( {a;b;c} \right)\) đi qua \(A\) có bán kính \(R = IA\), suy ra phương trình mặt cầu

\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = I{A^2}\)

Lời giải chi tiết:

Ta có \(IA = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( {0 - 2} \right)}^2} + {{\left( {4 - \left( { - 3} \right)} \right)}^2}}  = \sqrt {53} \)

Mặt cầu tâm \(I\left( {1;2; - 3} \right)\) có bán kính \(R = IA = \sqrt {53} \) có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 53.\)

Chọn D

Phương pháp giải:

Lời giải chi tiết:

* Giả sử \(M\left( {x;y;z} \right)\) ta có:

\(\begin{array}{l}\overrightarrow {MA}  = \left( {2 - x; - y; - z} \right)\\\overrightarrow {MB}  = \left( { - x;4 - y; - z} \right)\\\overrightarrow {MC}  = \left( { - x; - y;6 - z} \right)\\\overrightarrow {MD}  = \left( {2 - x;4 - y;6 - z} \right)\end{array}\)

\( \Rightarrow \overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = \left( { - 4x + 4; - 4y + 8; - 4z + 12} \right)\)

* \(\left| {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD} } \right| = 4\)

\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( { - 4x + 4} \right)}^2} + {{\left( { - 4y + 8} \right)}^2} + {{\left( { - 4z + 12} \right)}^2}}  = 4\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 1\end{array}\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

* Ta có \(I\left( {1; - 2;1} \right)\).

* Lập phương trình \(\left( d \right)\) đi qua \(I\) và vuông góc với \(\left( P \right)\).

   +) \(\overrightarrow {{a_d}}  = \overrightarrow {{n_P}}  = \left( {2;3;1} \right)\).

   +) \(d\) qua \(I \Rightarrow d:\,\,\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{3} = \dfrac{{z - 1}}{1}\).

* Giải hệ \(\left\{ \begin{array}{l}d\\\left( P \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}3x - 2y - 7 = 0\\x - 2z + 1 = 0\\2x + 3y + z - 11 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 3\\y = 1\\z = 2\end{array} \right. \Rightarrow T\left( {3;1;2} \right)\).

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

* Qua \(I\) vẽ đường thẳng \(\left( d \right)\) vuông góc với \(\left( P \right)\), đường thẳng \(\left( d \right)\) cắt \(\left( S \right)\) tại \(A,B\). Khi \(M \equiv A\) thì \(d\left( {M;\left( P \right)} \right)\) lớn nhất.

* Khoảng cách lớn nhất \( = IM + IH = R + d\left( {I;\left( P \right)} \right)\).

Ta có \(R = 2;\,\,d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {2 + 2 + 1 + 10} \right|}}{{\sqrt {4 + 4 + 1} }} = 5\).

\( \Rightarrow d{\left( {M;\left( P \right)} \right)_{\max }} = 2 + 5 = 7\).

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

* Gọi \(\left( P \right)\) là mặt phẳng chứa \(\left( C \right)\). Phương trình \(\left( P \right):\,\left( {{S_1}} \right) - \left( {{S_2}} \right)\)

\( \Rightarrow 2x + 2y + 2z - 3 = 0\).

* \({I_1}\left( {0;0;0} \right),\,\,{I_1}H = d\left( {{I_1};\left( P \right)} \right)3 = \dfrac{{\left| 3 \right|}}{{\sqrt {4 + 4 + 4} }} = \dfrac{3}{{\sqrt {12} }}\).

* Xét tam giác vuông \({I_1}AH:\,\,\)

\(AH = {R_C} = \sqrt {{I_1}{A^2} - {I_1}{H^2}}  = \sqrt {9 - \dfrac{9}{{12}}}  = \sqrt {\dfrac{{99}}{{12}}} \).

Chọn A.   

Phương pháp giải:

Lời giải chi tiết:

Mặt cầu \({x^2} + {y^2} + {(z - 1)^2} = 25\) có tâm \(I\left( {0;0;1} \right)\), bán kính \(R = 5\).

Gọi \(H\) là trung điểm của \(AB \Rightarrow IH \bot AB\).

Ta có: \(O{A^2} - O{B^2} = \left( {\overrightarrow {OA}  - \overrightarrow {OB} } \right)\left( {\overrightarrow {OA}  + \overrightarrow {OB} } \right) = \overrightarrow {BA} .2\overrightarrow {OH} \).

\( = \overrightarrow {BA} .2\left( {\overrightarrow {OI}  + \overrightarrow {IH} } \right) = 2\overrightarrow {BA} .\overrightarrow {OI}  + 2\overrightarrow {BA} .\overrightarrow {IH} \).

Do \(IH \bot AB \Rightarrow \overrightarrow {BA} .\overrightarrow {IH}  = 0 \Rightarrow O{A^2} - O{B^2} = 2\overrightarrow {BA} .\overrightarrow {OI} \).

\( = 2BA.OI.\cos \angle \left( {\overrightarrow {BA} ;\overrightarrow {OI} } \right) \le 2BA.OI = 2.6.\sqrt {{0^2} + {0^2} + {1^2}}  = 12\).

Vậy \(\max \left( {O{A^2} - O{B^2}} \right) = 12\).

Chọn A.

Phương pháp giải:

+) Gọi \(I\left( {a;b;c} \right)\) là tâm của mặt cầu \(\left( S \right)\). Mặt cầu \(\left( S \right)\) đi qua bốn điểm \(A,B,C,D \Rightarrow \left\{ \begin{array}{l}IA = IB\\IB = IC\\IC = ID\end{array} \right.\).

+) Giải hệ 3 phương trình tìm \(a;b;c\). Tính \(R = IA\).

Lời giải chi tiết:

Gọi \(I\left( {a;b;c} \right)\) là tâm của mặt cầu \(\left( S \right)\).

Mặt cầu \(\left( S \right)\) đi qua bốn điểm \(A,B,C,D \Rightarrow \left\{ \begin{array}{l}IA = IB\\IB = IC\\IC = ID\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\left( {a - 2} \right)^2} + {b^2} + {c^2} = {\left( {a - 1} \right)^2} + {\left( {b - 3} \right)^2} + {c^2}\\{\left( {a - 1} \right)^2} + {\left( {b - 3} \right)^2} + {c^2} = {\left( {a + 1} \right)^2} + {b^2} + {\left( {c - 3} \right)^2}\\{\left( {a + 1} \right)^2} + {b^2} + {\left( {c - 3} \right)^2} = {\left( {a - 1} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 4a + 4 =  - 2a + 1 - 6b + 9\\ - 2a + 1 - 6b + 9 = 2a + 1 - 6c + 9\\2a + 1 =  - 2a + 1 - 4b + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 2a + 6b = 6\\ - 4a - 6b + 6c = 0\\4a + 4b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 1\\c = 1\end{array} \right. \Rightarrow I\left( {0;1;1} \right)\\ \Rightarrow R = IA = \sqrt {{{\left( {a - 2} \right)}^2} + {b^2} + {c^2}}  = \sqrt {{2^2} + {1^2} + {1^2}}  = \sqrt 6 \end{array}\)

Chọn B

Phương pháp giải:

- Gọi \(E\) là trung điểm của \(AB\).

- Đánh giá GTNN của tích \(\overrightarrow {MA} .\overrightarrow {MB} \) đạt được dựa vào điểm \(E\).

Lời giải chi tiết:

Mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;2;1} \right)\) và bán kính \(R = \dfrac{{\sqrt 6 }}{2}\).

Gọi \(E\) là trung điểm của \(AB\) \( \Rightarrow E\left( {1; - 2; - 1} \right)\) và \(AB = 6\sqrt 2 \).

Ta có :

\(\overrightarrow {MA} .\overrightarrow {MB}  = \left( {\overrightarrow {ME}  + \overrightarrow {EA} } \right)\left( {\overrightarrow {ME}  + \overrightarrow {EB} } \right)\) \( = M{E^2} + \overrightarrow {ME} .\left( {\overrightarrow {EA}  + \overrightarrow {EB} } \right) + \overrightarrow {EA} .\overrightarrow {EB} \)

\( = M{E^2} + \overrightarrow {ME} .\overrightarrow 0  - \overrightarrow {EB} .\overrightarrow {EB}  = M{E^2} - \dfrac{1}{4}A{B^2}\)

Suy ra \(\overrightarrow {MA} .\overrightarrow {MB} \) đạt GTNN khi \(ME\) đạt GTNN.

Lại có : \(ME + MI \ge IE \Rightarrow ME + MI \ge IN + NE \Rightarrow ME \ge NE\)

\( \Rightarrow ME\) đạt \(GTNN\) khi \(M \equiv N\) với \(N = IE \cap \left( S \right)\).

Đường thẳng \(IE\) đi qua \(I\left( { - 1;2;1} \right)\) và nhận \(\overrightarrow {IE}  = \left( {2; - 4; - 2} \right)\) hay \(\dfrac{1}{2}\overrightarrow {IE}  = \left( {1; - 2; - 1} \right)\) làm VTCP nên \(IE:\left\{ \begin{array}{l}x =  - 1 + t\\y = 2 - 2t\\z = 1 - t\end{array} \right.\).

\(N = IE \cap \left( S \right)\) nên \({\left( { - 1 + t} \right)^2} + {\left( {2 - 2t} \right)^2} + {\left( {1 - t} \right)^2} + 2\left( { - 1 + t} \right) - 4\left( {2 - 2t} \right) - 2\left( {1 - t} \right) + \dfrac{9}{2} = 0\)

\( \Leftrightarrow 6{\left( {t - 1} \right)^2} + 12\left( {t - 1} \right) + \dfrac{9}{2} = 0\) \( \Leftrightarrow \left[ \begin{array}{l}t - 1 =  - \dfrac{1}{2}\\t - 1 =  - \dfrac{3}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{1}{2}\\t =  - \dfrac{1}{2}\end{array} \right.\)  \( \Rightarrow \left[ \begin{array}{l}N\left( { - \dfrac{1}{2};1;\dfrac{1}{2}} \right) \Rightarrow NE = \dfrac{{3\sqrt 6 }}{2}\\N\left( { - \dfrac{3}{2};3;\dfrac{3}{2}} \right) \Rightarrow NE = \dfrac{{5\sqrt 6 }}{2}\end{array} \right.\)

\(M{E_{\min }} = \dfrac{{3\sqrt 6 }}{2}\) khi \(M \equiv N\left( { - \dfrac{1}{2};1;\dfrac{1}{2}} \right)\) \( \Rightarrow a + b + c =  - \dfrac{1}{2} + 1 + \dfrac{1}{2} = 1\).

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

* Giả sử \(I\left( {a;b;c} \right)\).

\(\begin{array}{l}\left\{ \begin{array}{l}I \in \left( P \right) \Rightarrow 2a + 2b + c - 3 = 0\\IA = IB \Leftrightarrow {a^2} + {\left( {b - 1} \right)^2} + {\left( {c - 2} \right)^2} = {\left( {a - 2} \right)^2} + {\left( {b + 2} \right)^2} + {\left( {c - 1} \right)^2}\\IB = IC \Leftrightarrow {\left( {a - 2} \right)^2} + {\left( {b + 2} \right)^2} + {\left( {c - 1} \right)^2} = {\left( {a + 2} \right)^2} + {b^2} + {\left( {c - 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2a + 2b + c - 3 = 0\\4a - 6b - 2c = 4\\ - 8a + 4b =  - 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 2\\b = 3\\c =  - 7\end{array} \right. \Rightarrow I\left( {2;3; - 7} \right)\end{array}\)

* \(R = IA = \sqrt {4 + 4 + 81}  = \sqrt {89} \).

* Phương trình \(\left( S \right):\,\,{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 7} \right)^2} = 89\).

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

Giả sử \(I\left( {a;b;c} \right)\) là tâm mặt cầu \(\left( S \right)\), ta có: \(d\left( {I;\left( \alpha  \right)} \right) = d\left( {I;\left( \beta  \right)} \right) = d\left( {I;\left( \gamma  \right)} \right)\)

\( \Rightarrow R = \left| {a - 1} \right| = \left| {b - 1} \right| = \left| {c + 1} \right|\)

Do \(M\)thuộc miền \(x > 1,\,\,y > 1,\,\,z <  - 1\) và \(M \in \left( S \right)\) nên \(I\left( {a;b;c} \right)\) cũng thuộc miền \(x > 1,\,\,y > 1,\,\,z <  - 1\)\( \Rightarrow a > 1,\,\,b > 1,\,\,c <  - 1\) \( \Rightarrow \left\{ \begin{array}{l}a = R + 1\\b = R + 1\\c =  - R - 1\end{array} \right.\)

Mặt khác \(IM = R \Rightarrow {\left( {R - 1} \right)^2} + {\left( {R - 4} \right)^2} + {\left( {R - 1} \right)^2} = {R^2} \Leftrightarrow R = 3\).

Chọn: D  

Phương pháp giải:

Lời giải chi tiết:

* \({\overrightarrow a _{IM}} = \overrightarrow {{n_P}}  = \left( {1;2;2} \right)\) \( \Rightarrow \) Phương trình \(IM:\,\,\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z =  - 3 + 2t\end{array} \right.\).

* \(I \in IM \Rightarrow I\left( {t + 1;2t + 1;2t - 3} \right)\).

* \(IM = 3 \Leftrightarrow {t^2} + 4{t^2} + 4{t^2} = 9 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t =  - 1\end{array} \right.\)

\( \Rightarrow \left[ \begin{array}{l}I\left( {2;3; - 1} \right)\\I\left( {0; - 1; - 5} \right)\,\,\left( {Loai} \right)\end{array} \right.\).

* Phương trình \(\left( S \right):\,\,{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 9\).

Chọn A.

Phương pháp giải:

- Tìm tọa độ điểm \(I\) sao cho  \(3\overrightarrow{IA}+2\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\).

- Biến đổi \(3M{{A}^{2}}+2M{{B}^{2}}+M{{C}^{2}}\) qua dạng vecto và đánh giá giá trị nhỏ nhất của tổng.

Lời giải chi tiết:

+) Mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=1\) có tâm \(J\left( 1;1;1 \right)\), bán kính \(R=1\).

+) Tìm \(I\):  \(3\overrightarrow{IA}+2\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Leftrightarrow 6\overrightarrow{IA}+2\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{0}\Leftrightarrow \overrightarrow{IA}=-\frac{2\overrightarrow{AB}+\overrightarrow{AC}}{6}\)

Ta có: \(A\left( 0;1;1 \right),\,B\left( 3;0;-1 \right),\,C\left( 0;21;-19 \right)\Rightarrow \overrightarrow{IA}\left( -{{x}_{I}};1-{{y}_{I}};1-{{z}_{I}} \right),\,\,\overrightarrow{AB}\left( 3;-1;-2 \right),\,\,\overrightarrow{AC}\left( 0;20;-20 \right)\)

\(\Rightarrow \left\{ \begin{align}  & -{{x}_{I}}=-\frac{2.3+0}{6} \\ & 1-{{y}_{I}}=-\frac{2.\left( -1 \right)+20}{6} \\ & 1-{{z}_{I}}=-\frac{2.\left( -2 \right)+\left( -20 \right)}{6} \\\end{align} \right.\Rightarrow I\left( 1;4;-3 \right)\)

+) Ta có:

\(\begin{align}  & 3M{{A}^{2}}+2M{{B}^{2}}+M{{C}^{2}}=3{{\left( \overrightarrow{MI}+\overrightarrow{IA} \right)}^{2}}+2{{\left( \overrightarrow{MI}+\overrightarrow{IB} \right)}^{2}}+{{\left( \overrightarrow{MI}+\overrightarrow{IC} \right)}^{2}} \\ & =6M{{I}^{2}}+3I{{A}^{2}}+2I{{B}^{2}}+I{{C}^{2}}+2.\overrightarrow{MI}.\left( 3\overrightarrow{IA}+2\overrightarrow{IB}+\overrightarrow{IC} \right)=6M{{I}^{2}}+3I{{A}^{2}}+2I{{B}^{2}}+I{{C}^{2}}+2.\overrightarrow{MI}.\overrightarrow{0} \\ & =6M{{I}^{2}}+3I{{A}^{2}}+2I{{B}^{2}}+I{{C}^{2}} \\\end{align}\)

Để tổng trên là nhỏ nhất thì MI nhỏ nhất \(\Rightarrow M\)là giao điểm của đoạn thẳng \(IJ\) và  mặt cầu \(\left( S \right)\).

\(\overrightarrow{JI}=\left( 0;3;-4 \right)\)

\(\Rightarrow \)Tọa độ điểm \(M\)thuộc đoạn IJ có dạng \(\left( 1;1+3t;1-4t \right),\,\,t\in \left[ 0;1 \right]\)

Mặt khác \(M\in \left( S \right)\Rightarrow {{\left( 1-1 \right)}^{2}}+{{\left( 1-\left( 1+3t \right) \right)}^{2}}+{{\left( 1-\left( 1-4t \right) \right)}^{2}}=1\)

\(\Leftrightarrow {{t}^{2}}=\frac{1}{25}\Leftrightarrow \left[ \begin{align}  & t=\frac{1}{5} \\ & t=-\frac{1}{5}\,(L) \\\end{align} \right.\Leftrightarrow t=\frac{1}{5}\)  \(\Rightarrow M\left( 1;\frac{8}{5};\frac{1}{5} \right)\Rightarrow OM=\frac{3\sqrt{10}}{5}\).

Chọn: C

Phương pháp giải:

Lời giải chi tiết:

* Giả sử \(I\left( {a;b;c} \right)\) ta có \(\left\{ \begin{array}{l}IA = IB\\IB = IC\\IC = ID\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {a - 3} \right)^2} + {\left( {b - 3} \right)^2} + {c^2} = {\left( {a - 3} \right)^2} + {b^2} + {\left( {c - 3} \right)^2}\\{\left( {a - 3} \right)^2} + {b^2} + {\left( {c - 3} \right)^2} = {a^2} + {\left( {b - 3} \right)^2} + {\left( {c - 3} \right)^2}\\{a^2} + {\left( {b - 3} \right)^2} + {\left( {c - 3} \right)^2} = {\left( {a - 3} \right)^2} + {\left( {b - 3} \right)^2} + {\left( {c - 3} \right)^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l} - 6b + 9 =  - 6c + 9\\ - 6a + 9 =  - 6b + 9\\0 =  - 6a + 9\end{array} \right. \Leftrightarrow a = b = c = \dfrac{3}{2} \Rightarrow I\left( {\dfrac{3}{2};\dfrac{3}{2};\dfrac{3}{2}} \right)\).

* \(R = IA = \sqrt {\dfrac{9}{4} + \dfrac{9}{4} + \dfrac{9}{4}}  = \sqrt {\dfrac{{27}}{4}} \).

* Phương trình \(\left( S \right):\,\,{\left( {x - \dfrac{3}{2}} \right)^2} + {\left( {y - \dfrac{3}{2}} \right)^2} + {\left( {z - \dfrac{3}{2}} \right)^2} = \dfrac{{27}}{4}\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

* \(I \in \left( \Delta  \right) \Rightarrow I\left( { - 3t + 2;2t + 1;2t + 1} \right)\).

* \(\left( S \right)\) tiếp xúc với \(\left( P \right),\,\,\left( Q \right)\)\( \Rightarrow d\left( {I;\left( P \right)} \right) = d\left( {I;\left( Q \right)} \right)\).

\(\begin{array}{l} \Rightarrow \dfrac{{\left| { - 3t + 2 + 2\left( {2t + 1} \right) - 2\left( {2t + 1} \right) - 2} \right|}}{{\sqrt {1 + 4 + 4} }} = \dfrac{{\left| { - 3t + 2 + 2\left( {2t + 1} \right) - 2\left( {2t + 1} \right) + 4} \right|}}{{\sqrt {1 + 4 + 4} }}\\ \Leftrightarrow \left| { - 3t} \right| = \left| { - 3t + 6} \right| \Leftrightarrow  - 3t = 3t - 6 \Leftrightarrow t = 1 \Rightarrow I\left( { - 1;3;3} \right)\end{array}\)

* \(d = d\left( {I;\left( P \right)} \right) = \dfrac{3}{3} = 1\).

* Phương trình \(\left( S \right):\,\,{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = 1 \Leftrightarrow {x^2} + {y^2} + {z^2} + 2x - 6y - 6z + 18 = 0\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

* \(I\left( {0; - 1;1} \right) \Rightarrow IJ = d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {0 + 2 + 2 - 1} \right|}}{{\sqrt {1 + 4 + 4} }} = 1\).

* \({R_S} = \sqrt {{a^2} + {b^2} + {c^2} - d}  = \sqrt {1 + 1 + 23}  = 5\).

* \({R_C} = \sqrt {R_S^2 - I{J^2}}  = \sqrt {25 - 1}  = \sqrt {24} \).

Chọn B.

Phương pháp giải:

+) Kiểm tra điểm \(A\in \left( S \right)\)

+) Gọi điểm B có dạng \(B\left( 0;0;a \right)\in Oz\)

+) AB tiếp xúc với (S) tại A \(\Leftrightarrow AB\bot IA\Leftrightarrow \overrightarrow{AB}.\overrightarrow{IA}=0\) , giải phương trình tìm a.

Lời giải chi tiết:

Gọi \(B\left( 0;0;a \right)\in Oz\).

Ta thấy \({{\left( 1+1 \right)}^{2}}+{{\left( -1+2 \right)}^{2}}+{{\left( -6+3 \right)}^{2}}=14\Rightarrow A\in \left( S \right)\), mà AB tiếp xúc với (S) \(\Rightarrow AB\) tiếp xúc với (S) tại A.

\(\Rightarrow AB\bot IA\) tại A \(\Rightarrow \overrightarrow{AB}.\overrightarrow{IA}=0\) , với I là tâm của mặt cầu (S), \(I\left( -1;-2;-3 \right)\)

Ta có: \(\overrightarrow{AB}=\left( -1;1;a+6 \right),\,\,\overrightarrow{IA}=\left( 2;1;-3 \right)\)

\(\Leftrightarrow -2+1-3\left( a+6 \right)=0\Leftrightarrow -3a-19=0\Leftrightarrow a=-\frac{19}{3}\)

Vậy \(B\left( 0;0;-\frac{19}{3} \right)\)

Chọn A.

Phương pháp giải:

Gọi điểm \(B\left( x,y,z \right)\in \left( S \right)\).

Tam giác OAB đều \( \Leftrightarrow \left\{ \begin{array}{l}OA = OB\\OA = AB\end{array} \right.\), giải hệ phương trình tìm B.

Lời giải chi tiết:

Giả sử điểm \(B\left( x,y,z \right)\in \left( S \right)\).

Theo giả thiết ta có:

\(\left\{ \begin{array}{l}B \in \left( S \right)\\OA = OB\\OA = AB\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}B \in \left( S \right)\\O{A^2} = O{B^2}\\O{A^2} = A{B^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} - 4x - 4y - 4z = 0\\{4^2} + {4^2} + {0^2} = {x^2} + {y^2} + {z^2}\\{4^2} + {4^2} + {0^2} = {\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + {z^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} - 4x - 4y - 4z = 0\\{x^2} + {y^2} + {z^2} = 32\\{\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + {z^2} = 32\end{array} \right.\)

Giải hệ phương trình trên ta được hai nghiệm \(\left( a;b;c \right)\) là \(\left( 0;4;4 \right)\) hoặc \(\left( 4;0;4 \right)\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Gọi phương trình mặt phẳng cần tìm là \(\left( P \right):ax+by+cz+d=0.\)

Vì\(d\left( {B;\left( P \right)} \right) \)=\( d\left( {C ;\left( P \right)} \right) = 1\) suy ra \(mp\,\,\left( P \right)\)//\(BC\) hoặc đi qua trung điểm của \(BC.\)

TH1. Với \(mp\,\,\left( P \right)\)//\(BC\)\(\Rightarrow \,\,a=0\Rightarrow \,\,\left( P \right):by+cz+d=0\) suy ra \(d\left( A;\left( P \right) \right)=\frac{\left| 2b+c+d \right|}{\sqrt{{{b}^{2}}+{{c}^{2}}}}=2\)

Và \(d\left( B;\left( P \right) \right)=\frac{\left| -\,b+c+d \right|}{\sqrt{{{b}^{2}}+{{c}^{2}}}}=1\)\(\Rightarrow \)\(\left\{ \begin{align} & \left| 2b+c+d \right|=2\left| -\,b+c+d \right| \\& \left| -\,b+c+d \right|=\sqrt{{{b}^{2}}+{{c}^{2}}} \\\end{align} \right.\Leftrightarrow \)\(\left[ \begin{array}{l}
\left\{ \begin{array}{l}
4b = c + d\\
c + d = 0
\end{array} \right.\\
\left| { - \,b + c + d} \right| = \sqrt {{b^2} + {c^2}} 
\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}
3\left| b \right| = \sqrt {{b^2} + {c^2}} \\
\left| b \right| = \sqrt {{b^2} + {c^2}}
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
8{b^2} = {c^2} \Rightarrow c = \pm \,2\sqrt 2 \,b\\
c = 0 \Rightarrow d = 0
\end{array} \right.\)suy ra có ba mặt phẳng thỏa mãn. 

TH2. Mặt phẳng \(\left( P \right)\) đi qua trung điểm \(BC\)\(\Rightarrow \)\(\left( P \right):a\left( x-1 \right)+b\left( y+1 \right)+c\left( z-1 \right)=0\)

Do đó \(d\left( A;\left( P \right) \right)=\frac{3\left| b \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=2;\,\,\,d\left( B;\left( P \right) \right)=\frac{2\left| a \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=1\)

Suy ra \(\left\{ \begin{align} & 3\left| b \right|=4\left| a \right| \\& 2\left| a \right|=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}} \\\end{align} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}
3\left| b \right| = 4\left| a \right|\\
2\left| a \right| = \sqrt {{a^2} + {b^2} + {c^2}}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3\left| b \right| = 4\left| a \right|\\
3{a^2} = {b^2} + {c^2}
\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( * \right).\)

Chọn \(a=3\) suy ra 

\(\left( * \right) \Leftrightarrow \left\{ \begin{array}{l}
\left| b \right| = 4\\
{b^2} + {c^2} = 27
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b = \pm \,4\\
{c^2} = 11
\end{array} \right. \Rightarrow \left( {a;b;c} \right) = \left\{ \begin{array}{l}
\left( {3;4;\sqrt {11} } \right),\,\,\left( {3; - \,4;\sqrt {11} } \right)\\
\left( {3;4; - \,\sqrt {11} } \right),\,\,\left( {3; - \,4; - \,\sqrt {11} } \right)
\end{array} \right\}.\)

Vậy có tất cả 7 mặt phẳng thỏa mãn yêu cầu bài toán.

Chọn B.

Phương pháp giải:

+) Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất thì \(d{{\left( I;\left( P \right) \right)}_{\max }}.\)

+) Gọi H và K lần lượt là chân đường vuông góc của I trên (P) và trên đường thẳng AB. Ta có : \(IH\le IK\)

\(\Rightarrow d{{\left( I;\left( P \right) \right)}_{\max }}=I{{H}_{\max }}=IK\Leftrightarrow H\equiv K\)

Lời giải chi tiết:

\(\begin{align}  & B\in \left( P \right)\Rightarrow b-2=0\Leftrightarrow b=2 \\ & A\in \left( P \right)\Rightarrow 3a-2b+6c-2=0\Rightarrow a+2c=2\Rightarrow a=2-2c \\\end{align}\)

Khi đó mặt phẳng (P) có dạng : \(\left( P \right):\,\,\left( 2-2c \right)x+2y+cz-2=0\)

Mặt cầu \(\left( S \right)\) có tâm \(I\left( 1;2;3 \right)\), bán kính \(R=5\).

Gọi H và K lần lượt là chân đường vuông góc của I trên (P) và trên đường thẳng AB. Ta có : \(IH\le IK\)

Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất thì \(d{{\left( I;\left( P \right) \right)}_{\max }}=I{{H}_{\max }}=IK\Leftrightarrow H\equiv K.\)

Ta có : \(\overrightarrow{AB}=\left( -3;3;-6 \right)=-3\left( 1;-1;2 \right)\)

\(\Rightarrow \) Phương trình đường thẳng AB : \(\left\{ \begin{align}  & x=t \\  & y=1-t \\  & z=2t \\ \end{align} \right.,\,\,K\in AB\Rightarrow K\left( t;1-t;2t \right)\Rightarrow \overrightarrow{IK}=\left( t-1;-t-1;2t-3 \right)\)

Vì \(IK\bot AB\Rightarrow \overrightarrow{IK}.\overrightarrow{AB}=0\Rightarrow \left( t-1 \right)-\left( -t-1 \right)+2\left( 2t-3 \right)=0\Leftrightarrow 6t-6=0\Leftrightarrow t=1\Rightarrow K\left( 1;0;2 \right)\)

\(d{{\left( I;\left( P \right) \right)}_{\max }}=I{{H}_{\max }}=IK\Leftrightarrow H\equiv K\Rightarrow H\left( 1;0;2 \right)\Rightarrow \overrightarrow{IH}=\left( 0;-2;-1 \right)\) là 1 VTPT của (P).

\(\Rightarrow \overrightarrow{IH}\) và vector pháp tuyến \({{\overrightarrow{n}}_{\left( P \right)}}\,\left( 2-2c;2;c \right)\) cùng phương

\(\begin{array}{l}
\Rightarrow {\overrightarrow n _{\left( P \right)}} = k\overrightarrow {IH} \Rightarrow \left\{ \begin{array}{l}
2 - 2c = 0\\
2 = - 2k\\
c = - k
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
c = 1\\
k = - 1
\end{array} \right. \Rightarrow a = 2 - 2c = 0\\
\Rightarrow T = a + b + c = 0 + 2 + 1 = 3
\end{array}\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Giả sử (P) tiếp xúc với (S_1­), (S_2­) lần lượt tại A,B

Gọi \(IJ\cap \left( P \right)=M\) ta kiểm tra được J là trung điểm IM do \(\frac{IA}{JB}=\frac{MI}{MJ}=2\)  suy ra \(M\left( 2;1;9 \right)\)

Gọi \(\overrightarrow{n}=\left( a;b;c \right),\,\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}\ne 0 \right)\) suy ra \(\left( P \right):\,a\left( x-2 \right)+b\left( y-1 \right)+c\left( z-9 \right)=0\)

Ta có: \(\left\{ \begin{align}  & d\left( I;\left( P \right) \right)={{R}_{1}}=4 \\  & d\left( J;\left( P \right) \right)={{R}_{2}}=2 \\ \end{align} \right.\Rightarrow \frac{\left| c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=\frac{1}{2}\Leftrightarrow {{a}^{2}}+{{b}^{2}}=3{{c}^{2}}\Leftrightarrow {{\left( \frac{a}{c} \right)}^{2}}+{{\left( \frac{b}{c} \right)}^{2}}=3\left( 1 \right)\)

Ta có: \(d\left( O;\left( P \right) \right)=\frac{\left| 2a+b+9c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=\frac{\left| 2a+b+9c \right|}{2\left| c \right|}=\frac{1}{2}\left| \frac{2a}{c}+\frac{b}{c}+9 \right|\)

Đặt \(t=\frac{2a}{c}+\frac{b}{c}\Leftrightarrow \frac{b}{c}=t-\frac{2a}{c}\) ta được \(d\left( O;\left( P \right) \right)=\frac{1}{2}\left| t+9 \right|\)

Thay \(\frac{b}{c}=t-\frac{2a}{c}\) vào (1) ta thu được \({{\left( \frac{a}{c} \right)}^{2}}+{{\left( t-\frac{2a}{c} \right)}^{2}}=3\Leftrightarrow 5{{\left( \frac{a}{c} \right)}^{2}}-4\frac{a}{c}t+{{t}^{2}}-3=0\)

Để phương trình có nghiệm thì \(4{{t}^{2}}-5{{t}^{2}}+15\ge 0\Leftrightarrow -\sqrt{15}\le t\le \sqrt{15}\Leftrightarrow 0<9-\sqrt{15}\le t+9\le 9+\sqrt{15}\)

Suy ra \(\frac{9-\sqrt{15}}{2}\le d\left( O;\left( P \right) \right)\le \frac{9+\sqrt{15}}{2}\Rightarrow M=\frac{9+\sqrt{15}}{2};m=\frac{9-\sqrt{15}}{2}\)

Suy ra \(M+m=9\) .

Chọn B

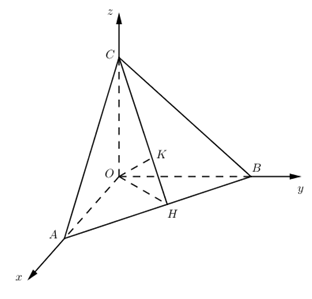
Phương pháp giải:

Gắn hệ tọa độ Oxyz, tìm bán kính quả bóng chính là bán kính của mặt cầu

Lời giải chi tiết:

Xét quả bóng tiếp xúc với các bức tường và chọn hệ trục \(Oxyz\) như hình vẽ bên (tương tự với góc tường còn lại).

Gọi \(I\left( a;a;a \right)\) là tâm của mặt cầu (tâm quả bóng) và \(R=a.\)

\(\Rightarrow \) phương trình mặt cầu của quả bóng là

\(\left( S \right):{{\left( x-a \right)}^{2}}+{{\left( y-a \right)}^{2}}+{{\left( z-a \right)}^{2}}={{a}^{2}}\,\,\,\,\,\,\,\,\,\,\left( 1 \right).\)

Giả sử \(M\left( x;y;z \right)\) nằm trên mặt cầu (bề mặt của quả bóng) sao cho \(d\left( M;\left( Oxy \right) \right)=1,\,\,d\left( M;\left( Oyz \right) \right)=2,\,\,d\left( M;\left( Oxz \right) \right)=3\)

Khi đó \(z=1;\,\,x=2;\,\,y=3\,\,\Rightarrow \,\,M\left( 2;3;1 \right)\in \left( S \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).\)

Từ \(\left( 1 \right),\left( 2 \right)\) suy ra \({{\left( 1-a \right)}^{2}}+{{\left( 2-a \right)}^{2}}+{{\left( 4-a \right)}^{2}}={{a}^{2}}\)

\(\Rightarrow \,\,\left\{ \begin{align}  & {{R}_{1}}={{a}_{1}}=\frac{7-\sqrt{7}}{2} \\ & {{R}_{2}}={{a}_{2}}=\frac{7+\sqrt{7}}{2} \\\end{align} \right.\Rightarrow \,\,{{d}_{1}}+{{d}_{2}}=2\left( {{R}_{1}}+{{R}_{2}} \right)=14.\)

Chọn B

Phương pháp giải:

Gọi tọa độ các điểm A, B, C.

Lập phương trình mặt phẳng đi qua H và cắt các trục Ox, Oy, Oz bằng phương trình đoạn chắn.

Từ đó tìm được các điểm A, B, C. Từ đó tính được bán kính mặt cầu ngoại tiếp tứ diện OABC.

Công thức tính diện tích mặt cầu bán kính \(R:\,\,S = 4\pi {R^2}.\)

Lời giải chi tiết:

Cách giải:

Gọi \(A\left( {a;\,\,0;\,\,0} \right),\,\,B\left( {0;\,b;\,0} \right),\,\,C\left( {0;\,0;\,c} \right)\) lần lượt thuộc các trục tọa độ \(Ox,\,Oy,\,Oz.\)

Khi đó ta có phương trình  \(\left( \alpha  \right)\) đi qua các điểm \(A,\,\,B,\,\,C:\,\,\,\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1.\)

\(H \in \left( \alpha  \right) \Rightarrow \frac{1}{a} + \frac{2}{b} - \frac{2}{c} = 1\,\,\,\,\,\left( 1 \right)\)

Theo đề bài ta có \(H\) là trực tâm \(\Delta ABC \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH}  \bot \overrightarrow {BC} \\\overrightarrow {BH}  \bot \overrightarrow {AC} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\\overrightarrow {BH} .\overrightarrow {AC}  = 0\end{array} \right..\)

Ta có: \(\left\{ \begin{array}{l}\overrightarrow {AH}  = \left( {1 - a;\,\,2; - 2} \right),\,\,\overrightarrow {BC}  = \left( {0; - b;\,\,c} \right)\\\overrightarrow {BH}  = \left( {1;\,2 - b; - 2} \right),\,\,\,\overrightarrow {AC}  = \left( { - a;\,0;\,c} \right)\end{array} \right.\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\\overrightarrow {BH} .\overrightarrow {AC}  = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2b - 2c = 0\\ - a - 2c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 2c\\b =  - c\end{array} \right.\\ \Rightarrow \left( 1 \right) \Leftrightarrow \frac{1}{{ - 2c}} + \frac{2}{{ - c}} - \frac{2}{c} = 1 \Rightarrow  - \frac{9}{{2c}} = 1 \Leftrightarrow c =  - \frac{9}{2}\\ \Rightarrow \left\{ \begin{array}{l}a =  - 2c = 9\\b =  - c = \frac{9}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A\left( {9;\,\,0;\,\,0} \right)\\B\left( {0;\,\frac{9}{2};\,0} \right)\\C\left( {0;\,0; - \frac{9}{2}} \right)\end{array} \right..\end{array}\)

Gọi \(I\left( {{x_0};\,{y_0};\,{z_0}} \right)\) là tâm mặt cầu ngoại tiếp hình chóp tứ giác \(OABC.\)

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Viết phương trình mặt phẳng (P) chứa (C) \(\Rightarrow K\in \left( P \right)\).

Gọi K là tâm của mặt cầu cần tìm ta có \(K\in \left( P \right)\). Gọi A’; B’; C’ lần lượt là hình chiếu của K trên AB, BC, CA.

Gọi K’ là hình chiếu của K trên (ABC), chứng minh K’ là trọng tâm tam giác ABC.

Viết phương trình đường thẳng d đi qua K’ và vuông góc với (ABC) \(\Rightarrow K\in d\).

\(\Rightarrow K=\left( P \right)\cap d\Rightarrow \) Tìm tọa độ điểm K.

Lời giải chi tiết:

Mặt cầu \(\left( {{S}_{1}} \right)\) có tâm \({{I}_{1}}\left( 1;1;0 \right)\), mặt cầu \(\left( {{S}_{2}} \right)\) có tâm \({{I}_{2}}\left( 4;-1;-1 \right)\).

Dễ thấy điểm \(M\left( 1;1;1 \right)\) thuộc cả hai mặt cầu \(\Rightarrow M\in \left( P \right)\,\,\,\left( 1 \right)\).

Mặt phẳng (P) chứa (C) vuông góc với \({{I}_{1}}{{I}_{2}}\) và đi qua M. Do đó phương trình mặt phẳng (P) là:

\(3\left( x-1 \right)-2\left( y-1 \right)-\left( z-1 \right)=0\Leftrightarrow 3x-2y-z=0\).

Gọi K là tâm của mặt cầu cần tìm ta có \(K\in \left( P \right)\). Gọi A’; B’; C’ lần lượt là hình chiếu của K trên AB, BC, CA ta có \(KA'=KB'=KC'\).

Gọi K’ là hình chiếu của K trên (ABC) ta  chứng minh được \(K'A\bot AB;\,\,K'B\bot BC;\,\,K'C\bot CA\) và \(K'A'=K'B'=K'C'\Rightarrow K'\) là tâm đường tròn nội tiếp tam giác ABC. Mà tam giác ABC đều \(\Rightarrow K'\) là trọng tâm của tam giác ABC \(\Rightarrow K'\left( 2;2;2 \right)\).

Phương trình mặt phẳng (ABC): \(\frac{x}{6}+\frac{y}{6}+\frac{z}{6}=1\Leftrightarrow x+y+z=6\).

\(\Rightarrow \) Phương trình đường thẳng đi qua K’ và vuông góc với (ABC) là: \(d:\,\,\frac{x-2}{1}=\frac{y-2}{1}=\frac{z-2}{1}\Rightarrow K\in d\,\,\,\left( 2 \right)\)

Từ (1) và (2) \(\Rightarrow K=\left( P \right)\cap d\Rightarrow K\left( t+2;t+2;t+2 \right)\)

Thay vào phương tình mặt phẳng (P) \(\Rightarrow 3\left( t+2 \right)-2\left( t+2 \right)-\left( t+2 \right)=0\Rightarrow \) Phương trình có vô số nghiệm.

Vậy có vô số điểm K thỏa mãn yêu cầu bài toán.

Chọn B.

Phương pháp giải:

 Tìm tọa độ tâm nội tiếp của tam giác qua đường phân giác hoặc công thức tính nhanh 

Lời giải chi tiết:

 Gọi \(I\) là tâm đường tròn nội tiếp tam giác \(OMN\).

Ta áp dụng tính chất sau : “ Cho tam giác \(OMN\) với \(I\) là tâm đường tròn nội tiếp tam giác OMN, ta có \(a.\overrightarrow{IO}+b.\overrightarrow{IM}+c.\overrightarrow{IN}=\overrightarrow{0}\), với \(a=MN\), \(b=ON\), \(c=OM\) ”.

Ta có \(OM=3,\) \(ON=4,\) \(MN=5\)\(\Rightarrow \)\(5.\overrightarrow{IO}+4.\overrightarrow{IM}+3.\overrightarrow{IN}=\overrightarrow{0}\) \(\Leftrightarrow \)\({{x}_{I}}=\frac{5.0+4.2+3.\left( \frac{-8}{3} \right)}{3+4+5}=0;\,\,\,{{y}_{I}}=\frac{5.0+4.2+3.\left( \frac{4}{3} \right)}{3+4+5}=1;\,\,\,{{z}_{I}}=\frac{5.0+4.2+3.\left( \frac{8}{3} \right)}{3+4+5}=1\)

Mặt phẳng \(\left( Oxz \right)\) có phương trình \(y=0\).

Mặt cầu tiếp xúc với mặt phẳng \(\left( Oxz \right)\) nên mặt cầu có bán kính \(R=d\left( I,\left( Oxz \right) \right)=1\).

Vậy phương trình mặt cầu là: \({{x}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=1\).

Chọn B

Phương pháp giải:

+) Công thức tính bán kính mặt cầu ngoại tiếp tam diện vuông tại \(A:\ \ R=IA=\frac{\sqrt{A{{B}^{2}}+A{{C}^{2}}+A{{D}^{2}}}}{2}.\)

+) Thể tích tam diện vuông: \({{V}_{ABCD}}=\frac{1}{6}AB.AC.AD.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow{IA}=\left( 1;\ 1;-1 \right)\Rightarrow R=IA=\sqrt{3}.\)

Lại có: \(A:\ \ R=IA=\frac{\sqrt{A{{B}^{2}}+A{{C}^{2}}+A{{D}^{2}}}}{2}=\sqrt{3}\Rightarrow A{{B}^{2}}+A{{C}^{2}}+A{{D}^{2}}=12\)

Áp dụng bất đẳng thức Cauchy ta có: \(A{{B}^{2}}+A{{C}^{2}}+A{{D}^{2}}\ge 3\sqrt[3]{A{{B}^{2}}.A{{C}^{2}}.A{{D}^{2}}}\)

\(\begin{align}  & \Leftrightarrow \sqrt[3]{A{{B}^{2}}.A{{C}^{2}}.A{{D}^{2}}}\le 4\Leftrightarrow AB.AC.AD\le 8. \\ & \Rightarrow {{V}_{ABCD}}=\frac{1}{6}AB.AC.AD\le \frac{1}{6}.8=\frac{4}{3}. \\\end{align}\)

Chọn C.

Phương pháp giải:

+) Gọi \(\overrightarrow n  = \left( {1;a;b} \right)\) là 1 VTPT của \(\left( P \right)\), viết phương trình mặt phẳng \(\left( P \right)\).

+) Tính các khoảng cách từ \(A,\,\,B,\,\,C\) đến \(\left( P \right)\) và sử dụng giả thiết \(\left\{ \begin{array}{l}d\left( {A;\left( P \right)} \right) = 3\\d\left( {B;\left( P \right)} \right) = 2\\d\left( {C;\left( P \right)} \right) = 3\end{array} \right.\), giải hệ tìm \(a,b\).

Lời giải chi tiết:

Gọi \(\overrightarrow n  = \left( {1;a;b} \right)\) là 1 VTPT của \(\left( P \right)\), khi đó phương trình \(\left( P \right)\) là:

\(1\left( {x - \dfrac{{14}}{5}} \right) + a\left( {y - \dfrac{2}{5}} \right) + b\left( {z - 3} \right) = 0 \Leftrightarrow 5x + 5ay + 5bz - 14 - 2a - 15b = 0\).

Theo bài ra ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}d\left( {A;\left( P \right)} \right) = 3\\d\left( {B;\left( P \right)} \right) = 2\\d\left( {C;\left( P \right)} \right) = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{\left| {5 - 10a + 15b - 14 - 2a - 15b} \right|}}{{\sqrt {25 + 25{a^2} + 25{b^2}} }} = 3\\\dfrac{{\left| {20 + 10a + 15b - 14 - 2a - 15b} \right|}}{{\sqrt {25 + 25{a^2} + 25{b^2}} }} = 2\\\dfrac{{\left| {15 + 20a + 15b - 14 - 2a - 15b} \right|}}{{\sqrt {25 + 25{a^2} + 25{b^2}} }} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{\left| { - 12a - 9} \right|}}{{5\sqrt {1 + {a^2} + {b^2}} }} = 3\\\dfrac{{\left| {8a + 6} \right|}}{{5\sqrt {1 + {a^2} + {b^2}} }} = 2\\\dfrac{{\left| {18a + 1} \right|}}{{5\sqrt {1 + {a^2} + {b^2}} }} = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{\left| {4a + 3} \right|}}{{5\sqrt {1 + {a^2} + {b^2}} }} = 1\\\dfrac{{\left| {4a + 3} \right|}}{{5\sqrt {1 + {a^2} + {b^2}} }} = 1\\\dfrac{{\left| {18a + 1} \right|}}{{5\sqrt {1 + {a^2} + {b^2}} }} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {4a + 3} \right| = 5\sqrt {1 + {a^2} + {b^2}} \\\left| {18a + 1} \right| = 15\sqrt {1 + {a^2} + {b^2}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {18a + 1} \right| = 3\left| {4a + 3} \right|\\\left| {4a + 3} \right| = 5\sqrt {1 + {a^2} + {b^2}} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}18a + 1 = 12a + 9\\18a + 1 =  - 12a - 9\end{array} \right.\\\left| {4a + 3} \right| = 5\sqrt {1 + {a^2} + {b^2}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = \dfrac{4}{3}\\a = \dfrac{{ - 1}}{3}\end{array} \right.\\\left| {4a + 3} \right| = 5\sqrt {1 + {a^2} + {b^2}} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = \dfrac{4}{3}\\\sqrt {\dfrac{{25}}{9} + {b^2}}  = \dfrac{5}{3}\end{array} \right.\\\left\{ \begin{array}{l}a =  - \dfrac{1}{3}\\\sqrt {\dfrac{{25}}{9} + {b^2}}  = \dfrac{1}{3}\,\,\left( {vo\,\,nghiem} \right)\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{4}{3}\\b = 0\end{array} \right.\end{array}\)

Vậy có 1 mặt phẳng thỏa mãn yêu cầu bài toán.

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Gọi điểm \(I\left( a;\,b;\,c \right)\) thỏa  mãn: \(\overrightarrow{IA}-\overrightarrow{IB}-\overrightarrow{IC}=\overrightarrow{0}.\)

\(\begin{array}{l}
\Leftrightarrow \left( {8 - a;\,\,5 - b; - 11 - c} \right) - \left( {5 - a;\,3 - b;\, - 4 - c} \right) - \left( {1 - 1;\,2 - b;\, - 6 - c} \right) = \overrightarrow 0 \\
\Leftrightarrow \left\{ \begin{array}{l}
8 - a - 5 + a - 1 + a = 0\\
5 - b - 3 + b - 2 + b = 0\\
- 11 - c + 4 + c + 6 + c = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = - 2\\
b = 0\\
c = 1
\end{array} \right. \Rightarrow I\left( { - 2;\,0;\,1} \right).
\end{array}\)

Theo đề bài ta có: \(\left| \overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC} \right|\,\,\,Min\)

\(\Rightarrow \left| \overrightarrow{MI}+\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}-\overrightarrow{MI}-\overrightarrow{IC} \right|=\left| 3\overrightarrow{MI}+\left( \overrightarrow{IA}-\overrightarrow{IB}-\overrightarrow{IC} \right) \right|=3\left| \overrightarrow{MI} \right|\,=3MI\,Min\)

Ta có: \(\left( S \right)\) có tâm \(J\left( 2;\,4;-1 \right),\,\,R=3.\) \(M\in \left( S \right)\Rightarrow M{{I}_{\min }}=IJ-R=\sqrt{16+16+4}-3=3.\)

Có: \(\overrightarrow{IJ}=\left( 4;\,4;-2 \right)=2\left( 2;\,2;-1 \right)\Rightarrow \) Phương trình đường thẳng \(IJ:\,\,\)\(\left\{ \begin{align}x=-2+2t \\ y=2t \\ z=1-t \\ \end{align} \right..\)

\(\begin{array}{l}
M \in IJ \Rightarrow M\left( { - 2 + 2t;\,2t;\,1 - t} \right)\\
M \in \left( S \right) \Rightarrow {\left( { - 4 + 2t} \right)^2} + {\left( {2t - 4} \right)^2} + {\left( {2 - t} \right)^2} = 9 \Leftrightarrow 9{\left( {t - 2} \right)^2} = 9\\
\Leftrightarrow {\left( {t - 2} \right)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}
t - 2 = 1\\
t - 2 = - 1
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
t = 3 \Rightarrow M\left( {4;\,6; - 2} \right)\\
t = 1 \Rightarrow M\left( {0;\,2;\,0} \right)
\end{array} \right.
\end{array}\)

Do \(MI=3\Rightarrow M\left( 0;\,2;\,0 \right)\) thỏa mãn \(\Rightarrow \left\{ \begin{align}a=0 \\ b=2 \\ \end{align} \right.\Rightarrow a+b=2.\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 3\) có tâm \(O\left( {0;0;0} \right)\) bán kính \(R = \sqrt 3 \).

Gọi \(H\) là điểm tiếp xúc của \(\left( S \right)\) và \(\left( P \right)\) \( \Rightarrow OH \bot \left( P \right) \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow H\) là trực tâm tam giác \(ABC\).

Trong \(\left( {ABC} \right)\), gọi \(E = CH \cap AB\), ta có: \(\left\{ \begin{array}{l}AB \bot CE\\AB \bot OH\end{array} \right. \Rightarrow AB \bot \left( {COE} \right) \Rightarrow AB \bot OE\).

Áp dụng hệ thức lượng trong tam giác vuông ta có:

\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} \Rightarrow \frac{1}{{O{H^2}}} = \frac{1}{{O{C^2}}} + \frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{3}\)

Mặt khác ta có: \(\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} \ge \frac{3}{{\sqrt[3]{{{{\left( {OA.OB.OC} \right)}^2}}}}} \ge \frac{3}{{\sqrt[3]{{{{\left( {\frac{{O{A^2} + O{B^2} + O{C^2}}}{3}} \right)}^3}}}}} = \frac{1}{3}\).

Dấu “=” xảy ra \( \Leftrightarrow OA = OB = OC = 3\).

\( \Rightarrow {V_{OABC}} = \frac{1}{6}OA.OB.OC = \frac{1}{6}.3.3.3 = \frac{9}{2}\).

Mà \({V_{OABC}} = \frac{1}{3}.OH.{S_{ABC}} \Rightarrow {S_{ABC}} = \frac{{3{V_{OABC}}}}{{OH}} = \frac{{3.\frac{9}{2}}}{{\sqrt 3 }} = \frac{{9\sqrt 3 }}{2}\).

Chọn B.