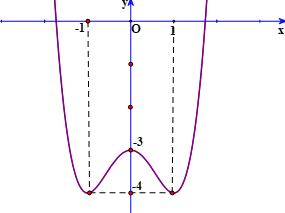
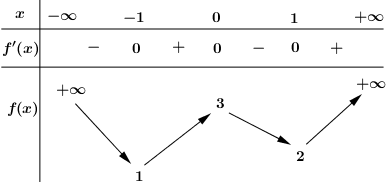
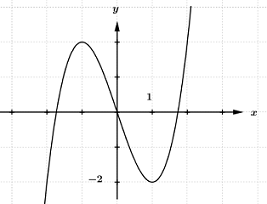
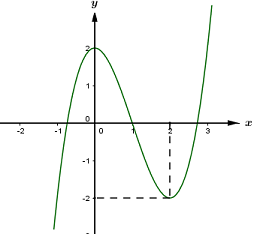
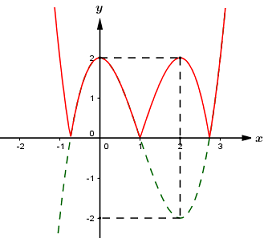
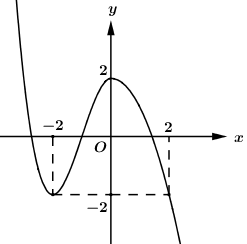
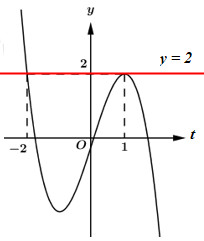
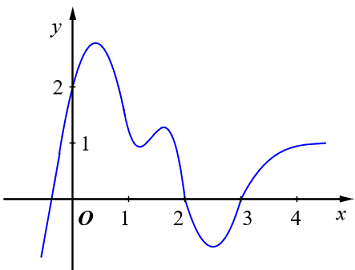
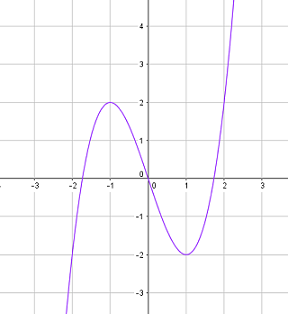
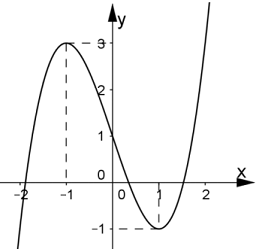
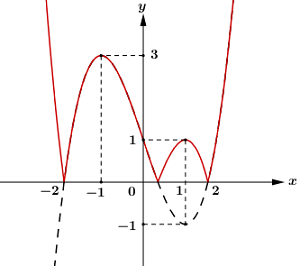
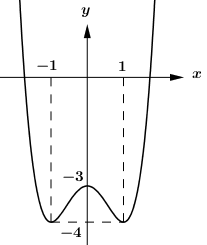
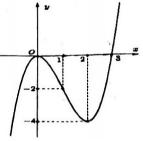
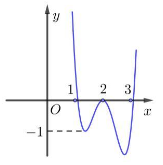
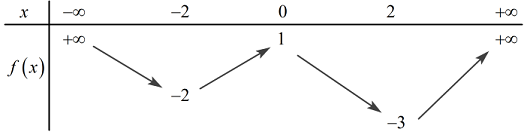
40 bài tập trắc nghiệm tương giao đồ thị hàm số mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Tìm \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có đúng hai nghiệm trên đoạn \(\left[ {0;\pi } \right]\).
Đáp án: A Phương pháp giải: - Đặt \(t = \sin x\), tìm điều kiện tương ứng của \(t\). - Tìm mối quan hệ giữa số nghiệm x với số nghiệm t, từ đó suy ra kết luận. Lời giải chi tiết: Đặt \(t = \sin x \in \left[ { - 1;1} \right]\). Dễ thấy với mỗi \(t \in \left[ {0;1} \right)\) thì sẽ có 2 giá trị \(x \in \left[ {0;\pi } \right]\). Do đó, để phương trình đã cho có đúng hai nghiệm trên đoạn \(\left[ {0;\pi } \right]\) thì phương trình \(f\left( t \right) = m\) có nghiệm duy nhất \(t \in \left[ {0;1} \right)\)\( \Leftrightarrow - 4 < m \le - 3\). Chọn A. Câu hỏi 2 : Cho hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(d:\,\,y = x + m\), \(m\)là tham số. Khi đường thẳng \(d\) cắt \(\left( C \right)\) tại hai điểm \(A\) và \(B\) sao cho tam giác \(OAB\) vuông tại \(O\)(\(O\)là gốc tọa độ) thì \(m\) thuộc khoảng nào dưới đây?
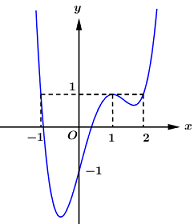
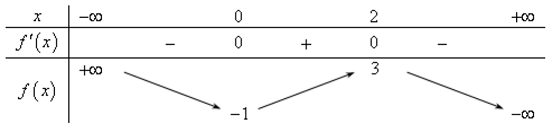
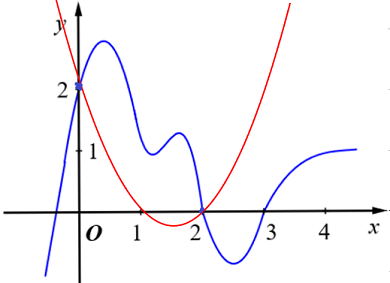
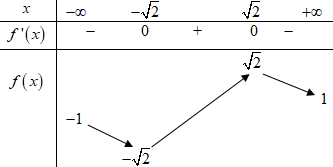
Đáp án: A Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình có 2 nghiệm phân biệt. - Áp dụng định lí Vi-et tìm tổng và tích hai nghiệm theo \(m\). - Tam giác \(OAB\) vuông tại \(O \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = 0\), giải phương trình suy ra m. Lời giải chi tiết: TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\). Xét phương trình hoành độ giao điểm \(\begin{array}{l}\,\,\,\,\,\,\frac{{2x - 1}}{{x - 1}} = x + m\,\,\,\left( {x \ne 1} \right)\\ \Leftrightarrow 2x - 1 = \left( {x + m} \right)\left( {x - 1} \right)\\ \Leftrightarrow 2x - 1 = {x^2} - x + mx - m\\ \Leftrightarrow f\left( x \right) = {x^2} + \left( {m - 3} \right)x - m + 1 = 0\,\,\,\left( * \right)\end{array}\) Để đường thẳng \(d\) cắt \(\left( C \right)\) tại 2 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 1. \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\Delta > 0\\f\left( 1 \right) \ne 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\left( {m - 3} \right)^2} - 4\left( {1 - m} \right) > 0\\1 + m - 3 - m + 1 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 6m + 9 - 4 + 4m > 0\\ - 1 \ne 0\,\,\left( {luon\,\,dung} \right)\end{array} \right.\end{array}\) \( \Leftrightarrow {m^2} - 2m + 5 > 0\) (luôn đúng với mọi \(m\)). Do đó phương trình (*) luôn có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\). Áp dụng định lý Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3 - m\\{x_1}.{x_2} = 1 - m\end{array} \right.\) Giả sử \(A\left( {{x_1};{x_1} + m} \right),\,\,B\left( {{x_2};{x_2} + m} \right)\) \( \Rightarrow \overrightarrow {OA} = \left( {{x_1};{x_1} + m} \right);\,\,\overrightarrow {OB} = \left( {{x_2};{x_2} + m} \right)\). Tam giác \(OAB\) vuông tại \(O \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = 0\) \(\begin{array}{l}\,\,\,\,\,\,\,{x_1}{x_2} + \left( {{x_1} + m} \right)\left( {{x_2} + m} \right) = 0\\ \Leftrightarrow {x_1}{x_2} + {x_1}{x_2} + m\left( {{x_1} + {x_2}} \right) + {m^2} = 0\\ \Leftrightarrow 2 - 2m + m\left( {3 - m} \right) + {m^2} = 0\\ \Leftrightarrow 2 - 2m + 3m - {m^2} + {m^2} = 0\\ \Leftrightarrow m + 2 = 0 \Leftrightarrow m = - 2\end{array}\) Vậy \(m = - 2 \in \left( { - 3; - \frac{1}{2}} \right)\). Chọn A. Câu hỏi 3 : Cho đồ thị hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(f'\left( x \right)\) như hình bên dưới.
Đặt \(g\left( x \right) = f\left( x \right) - x\), khẳng định nào sau đây đúng?
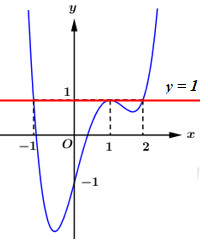
Đáp án: B Phương pháp giải: - Tính đạo hàm \(g'\left( x \right)\). - Dựa vào tương giao đồ thị hàm số để giải phương trình \(g'\left( x \right) = 0\). - Lập BBT hàm số và so sánh các giá trị. Lời giải chi tiết: Ta có \(g\left( x \right) = f\left( x \right) - x \Rightarrow g'\left( x \right) = f'\left( x \right) - 1\). Xét phương trình \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) - 1 = 0 \Leftrightarrow f'\left( x \right) = 1\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = 1\). Vẽ đồ thị hàm số \(y = f'\left( x \right)\) và \(y = 1\) trên cùng mặt phẳng tọa độ ta có:
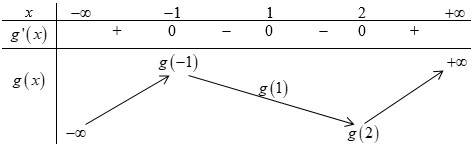
Dựa vào đồ thị hàm số ta thấy \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 2\end{array} \right.\). Ta có BBT hàm số \(y = g\left( x \right)\) như sau:
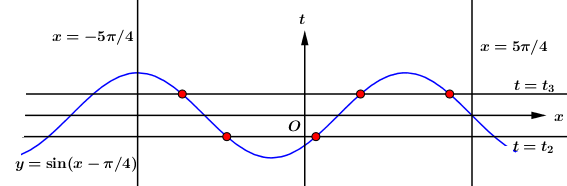
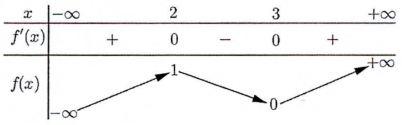
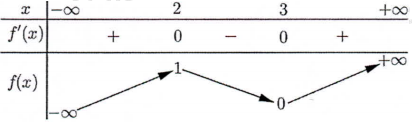
Dựa vào bảng biến thiên ta thấy \(g\left( { - 1} \right) > g\left( 1 \right) > g\left( 2 \right)\). Chọn B. Câu hỏi 4 : Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
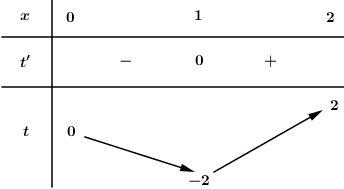
Số nghiệm thuộc đoạn \(\left[ { - \dfrac{{5\pi }}{4};\dfrac{{5\pi }}{4}} \right]\) của phương trình \(3f\left( {\dfrac{{\sin x - \cos x}}{{\sqrt 2 }}} \right) - 7 = 0\) là:
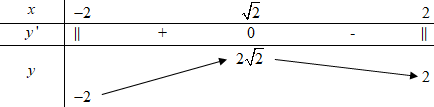
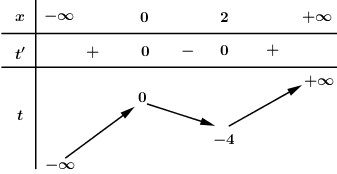
Đáp án: C Phương pháp giải: - Sử dụng biến đổi: \(\sin x - \cos x = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\). - Đặt ẩn phụ \(t = \sin \left( {x - \dfrac{\pi }{4}} \right)\), tìm khoảng giá trị của \(t\), đưa phương trình về dạng \(f\left( t \right) = m\). - Dựa vào BBT xác định số nghiệm \(t\) thỏa mãn điều kiện. - Lập BBT hoặc vẽ đồ thị hàm số \(t = \sin \left( {x - \dfrac{\pi }{4}} \right)\) trên \(\left[ { - \dfrac{{5\pi }}{4};\dfrac{{5\pi }}{4}} \right]\), với mỗi giá trị \(t\) tìm số nghiệm \(x\) tương ứng. Lời giải chi tiết: Ta có: \(3f\left( {\dfrac{{\sin x - \cos x}}{{\sqrt 2 }}} \right) - 7 = 0\) \( \Leftrightarrow f\left( {\sin \left( {x - \dfrac{\pi }{4}} \right)} \right) = \dfrac{7}{3}\). Đặt \(t = \sin \left( {x - \dfrac{\pi }{4}} \right)\) . Với \(x \in \left[ { - \dfrac{{5\pi }}{4};\dfrac{{5\pi }}{4}} \right]\) \( \Rightarrow x - \dfrac{\pi }{4} \in \left[ { - \dfrac{{3\pi }}{2};\pi } \right]\) \( \Rightarrow \sin \left( {x - \dfrac{\pi }{4}} \right) \in \left[ { - 1;1} \right]\) \( \Rightarrow t \in \left[ { - 1;1} \right]\). Phương trình trở thành \(f\left( t \right) = \dfrac{7}{3}\,\,\,\left( * \right),\,\,t \in \left[ { - 1;1} \right]\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = \dfrac{7}{3}\). Dựa vào BBT ta thấy phương trình (*) có 4 nghiệm phân biệt \(\left[ \begin{array}{l}t = {t_1} \in \left( { - \infty ; - 1} \right)\,\,\left( {ktm} \right)\\t = {t_2} \in \left( { - 1;0} \right)\,\,\,\,\,\,\,\left( {tm} \right)\\t = {t_3} \in \left( {0;1} \right)\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\t = {t_4} \in \left( {1; + \infty } \right)\,\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\). Ta có đồ thị hàm số \(t = \sin \left( {x - \dfrac{\pi }{4}} \right)\) trên đoạn \(\left[ { - \dfrac{{5\pi }}{4};\dfrac{{5\pi }}{4}} \right]\) như sau:
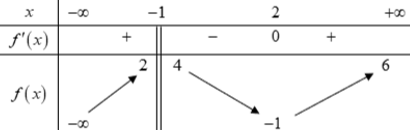
Dựa vào đồ thị hàm số ta thấy: + Phương trình \(t = {t_2} \Leftrightarrow \sin \left( {x - \dfrac{\pi }{4}} \right) = {t_2}\) có 2 nghiệm phân biệt. + Phương trình \(t = {t_3} \Leftrightarrow \sin \left( {x - \dfrac{\pi }{4}} \right) = {t_3}\) có 3 nghiệm phân biệt. Vậy phương trình ban đầu có 5 nghiệm phân biệt. Chọn C. Câu hỏi 5 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ dưới đây:
Số giá trị nguyên của tham số \(m\) để phương trình \(f\left( {3 - x} \right) = m\) có đúng hai nghiệm phân biệt là:
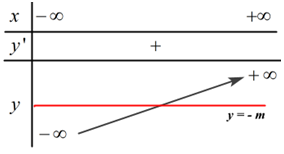
Đáp án: D Phương pháp giải: - Đặt \(t = 3 - x\), đưa phương trình về dạng \(f\left( t \right) = m\,\,\left( * \right)\). - Để phương trình ban đầu có đúng 2 nghiệm phân biệt thì phương trình (*) cũng phải có đúng 2 nghiệm phân biệt \( \Rightarrow \) Đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại đúng 2 điểm phân biệt. Dựa vào BBT suy ra các giá trị của \(m\) thỏa mãn. Lời giải chi tiết: Đặt \(t = 3 - x\), phương trình trở thành \(f\left( t \right) = m\,\,\left( * \right)\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = m\). Để phương trình ban đầu có đúng 2 nghiệm phân biệt thì phương trình (*) cũng phải có đúng 2 nghiệm phân biệt \( \Rightarrow \) Đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại đúng 2 điểm phân biệt \( \Rightarrow \left[ \begin{array}{l}m = - 1\\2 < m \le 4\end{array} \right.\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;3;4} \right\}\). Vậy có 3 giá trị của \(m\) thỏa mãn yêu cầu bài toán. Chọn D. Câu hỏi 6 : Có tất cả bao nhiêu số nguyên \(m\) thỏa mãn đồ thị hàm số \(y = {x^3} + 2020x + m\) và trục hoành có điểm chung?
Đáp án: A Phương pháp giải: Đồ thị hàm số \(y = {x^3} + 2020x + m\) và trục hoành có điểm chung \( \Leftrightarrow \) phương trình hoành độ giao điểm của hai đồ thị hàm số \({x^3} + 2020x + m = 0\) \( \Leftrightarrow {x^3} + 2020x = - m\) có nghiệm. \( \Leftrightarrow \) Đường thẳng \(y = - m\) và đồ thị hàm số \(y = {x^3} + 2020x\) có điểm chung. Lập BBT rồi xác định số giá trị của \(m\) thỏa mãn bài toán. Lời giải chi tiết: Đồ thị hàm số \(y = {x^3} + 2020x + m\) và trục hoành có điểm chung \( \Leftrightarrow \) phương trình hoành độ giao điểm của hai đồ thị hàm số \({x^3} + 2020x + m = 0\) \( \Leftrightarrow {x^3} + 2020x = - m\) có nghiệm. \( \Leftrightarrow \) Đường thẳng \(y = - m\) và đồ thị hàm số \(y = {x^3} + 2020x\) có điểm chung. Xét hàm số \(y = {x^3} + 2020x\) ta có: \(y' = 3{x^2} + 2020 > 0\,\,\forall x\) \( \Rightarrow \) Hàm số \(y = {x^3} + 2020x\) đồng biến trên \(\mathbb{R}.\) Ta có BBT: \( \Rightarrow \) Với mọi giá trị của \(m\) thì đường thẳng \(y = - m\) cắt đồ thị hàm số \(y = {x^3} + 2020x\) tại 1 điểm. Vậy có vô số giá trị của \(m\) thỏa mãn bài toán. Chọn A. Câu hỏi 7 : Gọi T là tập hợp tất cả các giá trị nguyên của tham số m để phương trình \({x^3} - 3{x^2} - {m^3} + 3{m^2} = 0\) có ba nghiệm phân biệt. Tổng tất cả các phần tử của T bằng
Đáp án: A Phương pháp giải: - Phân tích vế trái của phương trình thành nhân tử. - Từ đó tìm điều kiện của m để phương trình có 3 nghiệm phân biệt. Lời giải chi tiết: Ta có: \(\begin{array}{l}{x^3} - 3{x^2} - {m^3} + 3{m^2} = 0\\ \Leftrightarrow \left( {{x^3} - {m^3}} \right) - 3\left( {{x^2} - {m^2}} \right) = 0\\ \Leftrightarrow \left( {x - m} \right)\left( {{x^2} + mx + {m^2}} \right)\\ - 3\left( {x - m} \right)\left( {x + m} \right) = 0\\ \Leftrightarrow \left( {x - m} \right)\left( {{x^2} + mx + {m^2} - 3x - 3m} \right) = 0\\ \Leftrightarrow \left( {x - m} \right)\left[ {{x^2} + \left( {m - 3} \right)x + {m^2} - 3m} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - m = 0\\{x^2} + \left( {m - 3} \right)x + {m^2} - 3m = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = m\\{x^2} + \left( {m - 3} \right)x + {m^2} - 3m = 0\,\,\left( 1 \right)\end{array} \right.\end{array}\) Đặt \(f\left( x \right) = {x^2} + \left( {m - 3} \right)x + {m^2} - 3m\). Để pt đã cho có 3 nghiệm phân biệt thì (1) có 2 nghiệm phân biệt khác \(m\)\( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\f\left( m \right) \ne 0\end{array} \right.\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 3} \right)^2} - 4\left( {{m^2} - 3m} \right) > 0\\{m^2} + \left( {m - 3} \right).m + {m^2} - 3m \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 3} \right)^2} - 4m\left( {m - 3} \right) > 0\\{m^2} + {m^2} - 3m + {m^2} - 3m \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 3} \right)\left( {m - 3 - 4m} \right) > 0\\3{m^2} - 6m \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 3} \right)\left( { - 3m - 3} \right) > 0\\3m\left( {m - 2} \right) \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 1 < m < 3\\m \ne 0,m \ne 2\end{array} \right.\end{array}\) Do \(m \in \mathbb{Z}\) nên \(m = 1\) hay \(T = \left\{ 1 \right\}\). Vậy tổng các phần tử của T là 1. Chọn A. Câu hỏi 8 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ
Phương trình \(\left| {f\left( {3x + 1} \right) - 2} \right| = 5\) có bao nhiêu nghiệm?
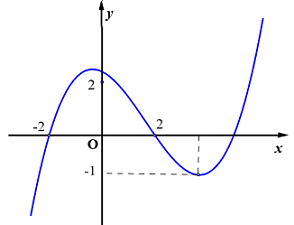
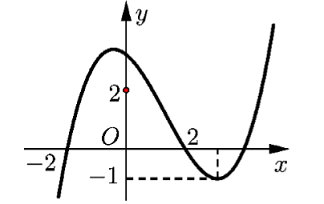
Đáp án: A Phương pháp giải: Phương trình \(\left| {h\left( x \right)} \right| = m > 0 \Leftrightarrow \left[ \begin{array}{l}h\left( x \right) = m\\h\left( x \right) = - m\end{array} \right.\) Lời giải chi tiết: Đặt \(t = 3x + 1\). Dễ thấy với mỗi \(x\) chỉ có một \(x\) và ngược lại. Do đó số nghiệm \(x\) của phương trình đã cho bằng số nghiệm \(t\) của phương trình \(\left| {f\left( t \right) - 2} \right| = 5\) Ta có: \(\left| {f\left( t \right) - 2} \right| = 5\) \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}f\left( t \right) - 2 = 5\\f\left( t \right) - 2 = - 5\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}f\left( t \right) = 7\,\,\,\left( 1 \right)\\f\left( t \right) = - 3\,\,\left( 2 \right)\end{array} \right.\end{array}\) Từ bbt ta thấy, +) Đường thẳng \(y = 7\) cắt đồ thị hàm số tại duy nhất 1 điểm nên (1) có 1 nghiệm. +) Đường thẳng \(y = - 3\) cắt đồ thị hàm số tại 2 điểm nên (2) có 2 nghiệm. Dễ thấy các nghiệm của (1) và (2) phân biệt. Vậy phương trình đã cho có tất cả 3 nghiệm. Chọn A. Câu hỏi 9 : Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có đồ thị như hình vẽ. Phương trình \(f\left( {f\left( x \right)} \right) = 0\) có tất cả bao nhiêu nghiệm thực?
Đáp án: D Phương pháp giải: - Giải phương trình tìm nghiệm của \(f\left( t \right) = 0\). - Giải phương trình nghiệm của \(f\left( x \right) = t\). Lời giải chi tiết: Ta có \(f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a \in \left( { - 2; - 1} \right)\\f\left( x \right) = b \in \left( {0;1} \right)\\f\left( x \right) = c \in \left( {1;2} \right)\end{array} \right.\) Dựa vào đồ thị hàm số ta có: +) \(f\left( x \right) = a \in \left( { - 2; - 1} \right)\) có 1 nghiệm. +) \(f\left( x \right) = b \in \left( {0;1} \right)\) có 3 nghiệm phân biệt. +) \(f\left( x \right) = c \in \left( {1;2} \right)\) có 3 nghiệm phân biệt. Vậy tổng tất cả có \(7\) nghiệm phân biệt. Chọn D. Câu hỏi 10 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.
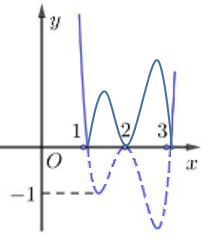
Đáp án: C Phương pháp giải: - Vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\). + Vẽ đồ thị hàm số \(y = f\left( x \right)\). + Xóa đi phần đồ thị hàm số nằm ở bên trái trục tung. + Lấy đối xứng phần đồ thị hàm số nằm ở bên phải trục tung qua trục tung. - Biện luận nghiệm để tìm tham số m: Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành. Lời giải chi tiết: Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta suy ra được đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như sau:
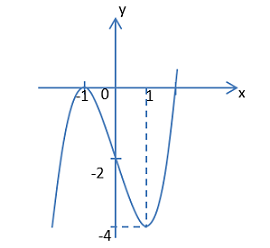
Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành. Do đó để phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có 4 nghiệm phân biệt thì \( - 2 < 3m + 1 < 0 \Leftrightarrow - 1 < m < - \dfrac{1}{3}\). Chọn C. Câu hỏi 11 : Có bao nhiêu giá trị nguyên dương của m để phương trình \(\left| {{x^3} - 3{x^2} + 2} \right| = m\) có đúng 6 nghiệm thực phân biệt.
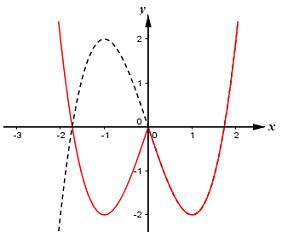
Đáp án: B Phương pháp giải: - Khảo sát và vẽ đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\). - Từ đó vẽ đồ thị hàm số \(y = \left| {{x^3} - 3{x^2} + 2} \right|\) như sau: + Vẽ đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\). + Lấy đối xứng phần đồ thị nằm phía dưới trục Ox qua trục Ox. + Xóa đi phần đồ thị phía dưới trục Ox. - Dựa đồ thị hàm số \(y = \left| {{x^3} - 3{x^2} + 2} \right|\) biện luận để phương trình \(\left| {{x^3} - 3{x^2} + 2} \right| = m\) có 6 nghiệm phân biệt. Lời giải chi tiết: Số nghiệm của phương trình \(\left| {{x^3} - 3{x^2} + 2} \right| = m\) là số giao điểm của đồ thị hàm số \(y = \left| {{x^3} - 3{x^2} + 2} \right|\) và đường thẳng \(y = m\) song song với trục hoành. Xét hàm số \(y = {x^3} - 3{x^2} + 2\) ta có: + TXĐ: \(D = \mathbb{R}\). + \(y' = 3{x^2} - 6x\), \(y' = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\). + \(\left\{ \begin{array}{l}x = 0 \Rightarrow y = 2\\x = 2 \Rightarrow y = - 2\end{array} \right.\) Ta vẽ được đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) như sau:
Từ đó ta vẽ được đồ thị hàm số \(y = \left| {{x^3} - 3{x^2} + 2} \right|\) như sau:
(Đường màu đỏ) Dựa vào đồ thị hàm số ta thấy phương trình \(\left| {{x^3} - 3{x^2} + 2} \right| = m\) có 6 nghiệm phân biệt khi và chỉ khi \(0 < m < 2\). Mà m nguyên dương \( \Rightarrow m = 1\). Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán. Chọn B. Câu hỏi 12 : Gọi S là diện tích hình phẳng giới hạn bởi đường thẳng x = 0 và đồ thị các hàm số \(y = \sqrt x \) và \(y = 6 - x\). Khẳng định nào sau đây là đúng?
Đáp án: D Phương pháp giải: - Xét phương trình hoành độ giao điểm để tìm cận còn lại. - Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và các đường thẳng \(x = a,\,\,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \(\sqrt x = 6 - x\,\,\left( {0 \le x \le 6} \right)\) \( \Leftrightarrow x = 36 - 12x + {x^2}\)\( \Leftrightarrow {x^2} - 13x + 36 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 9\,\,\left( {ktm} \right)\\x = 4\,\,\left( {tm} \right)\end{array} \right.\). Do đó hình phẳng cần tính được giới hạn bởi các đồ thị hàm số \(y = \sqrt x \), \(y = 6 - x\), đường thẳng \(x = 0\), \(x = 4\), có diện tích là \(S = \int\limits_0^4 {\left| {\sqrt x - 6 + x} \right|dx} \). Với \(x \in \left[ {0;4} \right]\) thì \(\sqrt x - 6 + x \le 0\), do đó \(\left| {\sqrt x - 6 + x} \right| = 6 - x - \sqrt x \). Vậy \(S = \int\limits_0^4 {\left( {6 - x - \sqrt x } \right)dx} \). Chọn D. Câu hỏi 13 : Cho hàm số \(f\left( x \right)\) có bảng biến thiên sau
Tìm tất cả các giá trị của tham số m để phương trình \(f\left( {2\tan x} \right) = 2m + 1\) có nghiệm thuộc khoảng \(\left( {0;\dfrac{\pi }{4}} \right)\)?
Đáp án: D Phương pháp giải: - Đặt ẩn phụ \(t = 2\tan x\), tìm khoảng giá trị của t ứng với \(x \in \left( {0;\dfrac{\pi }{4}} \right)\). - Số nghiệm của phương trình \(f\left( t \right) = 2m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = 2m + 1\) song song với trục hoành. Lời giải chi tiết: Đặt \(t = 2\tan x\), với \(x \in \left( {0;\dfrac{\pi }{4}} \right)\) thì \(\tan x \in \left( {0;1} \right) \Rightarrow t \in \left( {0;2} \right)\). Khi đó phương trình trở thành: \(f\left( t \right) = 2m + 1\), số nghiệm của phương trình \(f\left( t \right) = 2m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = 2m + 1\) song song với trục hoành. Quan sát BBT trên khoảng (0;2), ta thấy, phương trình có nghiệm \( \Leftrightarrow - 1 < 2m + 1 < 3 \Leftrightarrow - 1 < m < 1\). Chọn D. Câu hỏi 14 : Cho hàm số \(y = f\left( x \right)\) có đồ thị trong hình sau:
Số nghiệm của phương trình \(f\left( {{x^3} - 3x} \right) + 1 = 0\) trong khoảng \(\left( {0;2} \right)\) là:
Đáp án: C Phương pháp giải: - Đặt ẩn phụ \(t = {x^3} - 3x\), lập BBT của hàm số \(t\left( x \right)\) trên khoảng \(\left( {0;2} \right)\). - Thay \(t = {x^3} - 3x\) vào phương trình đề bài cho, giải phương trình tìm \(t\). - Từ các nghiệm \(t\) tìm được sử dụng phương pháp tương giao để tìm số nghiệm \(x\). Lời giải chi tiết: Đặt \(t = {x^3} - 3x\) ta có \(t' = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left( {0;2} \right)\\x = - 1 \notin \left( {0;2} \right)\end{array} \right.\). Ta có BBT:
Suy ra \(x \in \left( {0;2} \right)\) thì \(t \in \left[ { - 2;2} \right)\). Khi đó phương trình trở thành \(f\left( t \right) + 1 = 0 \Leftrightarrow f\left( t \right) = - 1\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = - 1\). Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại 3 điểm phân biệt, do đó phương trình \(f\left( t \right) = - 1\) có 3 nghiệm phân biệt \(\left[ \begin{array}{l}t = a \in \left( { - \infty ; - 2} \right)\,\,\left( {ktm} \right)\\t = b \in \left( { - 2;0} \right)\\t = c \in \left( {0;2} \right)\end{array} \right.\). Dựa vào BBT hàm số \(t = {x^3} - 3x\) ta có: + Phương trình \(t = b \in \left( { - 2;0} \right)\) có 2 nghiệm phân biệt. + Phương trình \(t = c \in \left( {0;2} \right)\) có 1 nghiệm duy nhất. Vậy phương trình đã cho có tất cả 3 nghiệm. Chọn C. Câu hỏi 15 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( {1 - f\left( x \right)} \right) = 2\) là:
Đáp án: D Phương pháp giải: - Đặt \(t = 1 - f\left( x \right)\), đưa phương trình về dạng phương trình ẩn \(t\). - Tìm số nghiệm của phương trình thông qua số giao điểm của đồ thị hàm số. - Từ nghiệm \(t\) tìm được thay lại phương trình \(f\left( x \right) = 1 - t\) để tìm số nghiệm \(x\), tiếp tục áp dụng phương pháp tương giao. Lời giải chi tiết: Đặt \(t = 1 - f\left( x \right)\), phương trình trở thành \(f\left( t \right) = 2\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = 2\).
Dựa vào đồ thị hàm số ta thấy \(f\left( t \right) = 2 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = - 2\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}1 - f\left( x \right) = 1\\1 - f\left( x \right) = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\,\,\,\left( 1 \right)\\f\left( x \right) = 3\,\,\,\left( 2 \right)\end{array} \right.\). + Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 0\) nên phương trình (1) có 3 nghiệm phân biệt. + Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 3\) nên phương trình (1) có 1 nghiệm duy nhất. Vậy phương trình đã cho có tất cả 4 nghiệm. Chọn D. Câu hỏi 16 : Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau: Số nghiệm thực của phương trình \(3f\left( x \right) - 2 = 0\) là:
Đáp án: C Phương pháp giải: Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) có tính chất song song với trục hoành. Lời giải chi tiết: Ta có: \(3f\left( x \right) - 2 = 0 \Leftrightarrow f\left( x \right) = \dfrac{2}{3}\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = \dfrac{2}{3}\) có tính chất song song với trục hoành. Vì \(0 < \dfrac{2}{3} < 1\) nên đường thẳng \(y = \dfrac{2}{3}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt. Vậy phương trình đã cho có 3 nghiệm phân biệt. Chọn C. Câu hỏi 17 : Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau: Số nghiệm thực của phương trình \(3f\left( x \right) - 2 = 0\) là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Câu hỏi 18 : Tìm tất cả các giá trị của tham số \(m\) để phương trình \(x - m - \sqrt {9 - {x^2}} = 0\) có đúng 1 nghiệm?
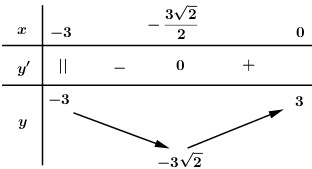
Đáp án: D Phương pháp giải: - Tìm ĐKXĐ. - Cô lập \(m\), đưa phương trình về dạng \(f\left( x \right) = m\). Khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) có tính chất song song với trục hoành. - Khảo sát và lập BBT của hàm số \(y = f\left( x \right)\) và kết luận. Lời giải chi tiết: ĐKXĐ: \(9 - {x^2} \ge 0 \Leftrightarrow - 3 \le x \le 3\). Ta có: \(x - m - \sqrt {9 - {x^2}} = 0 \Leftrightarrow x - \sqrt {9 - {x^2}} = m\,\,\left( * \right)\). Khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = x - \sqrt {9 - {x^2}} \) và đường thẳng \(y = m\) có tính chất song song với trục hoành. Xét hàm số \(y = x - \sqrt {9 - {x^2}} \) với \( - 3 \le x \le 3\) ta có \(y' = 1 + \dfrac{x}{{\sqrt {9 - {x^2}} }} = \dfrac{{\sqrt {9 - {x^2}} + x}}{{\sqrt {9 - {x^2}} }}\). Cho \(y' = 0 \Leftrightarrow \sqrt {9 - {x^2}} + x = 0\) \( \Leftrightarrow \sqrt {9 - {x^2}} = - x\) \( \Leftrightarrow \left\{ \begin{array}{l} - x \ge 0\\9 - {x^2} = {x^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\x = \pm \dfrac{{3\sqrt 2 }}{2}\end{array} \right.\) \( \Leftrightarrow x = - \dfrac{{3\sqrt 2 }}{2}\). Ta có BBT:
Dựa vào BBT ta thấy phương trình (*) có đúng 1 nghiệm khi và chỉ khi \(m = - 3\sqrt 2 \). Vậy \(m = - 3\sqrt 2 \). Chọn D. Câu hỏi 19 : Có tất cả bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 2020;2020} \right]\) của tham số m để đường thẳng \(y = x + m\) cắt đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x - 1}}\) tại hai điểm phân biệt?
Đáp án: A Phương pháp giải: - Tìm TXĐ. - Xét phương trình hoành độ giao điểm, đưa phương trình về dạng phương trình bậc hai ẩn x. - Tìm điều kiện để phương trình có hai nghiệm phân biệt thỏa mãn TXĐ. - Đối chiếu điều kiện đề bài để tìm các số nguyên m thỏa mãn. Lời giải chi tiết: TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\). Xét phương trình hoành độ giao điểm: \(\begin{array}{l}\dfrac{{2x - 3}}{{x - 1}} = x + m\,\,\left( {x \ne 1} \right)\\ \Leftrightarrow 2x - 3 = \left( {x - 1} \right)\left( {x + m} \right)\\ \Leftrightarrow 2x - 3 = {x^2} + mx - x - m\\ \Leftrightarrow {x^2} + \left( {m - 3} \right)x - m + 3 = 0\,\,\,\left( * \right)\end{array}\) Để để đường thẳng \(y = x + m\) cắt đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x - 1}}\) tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 1 \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\Delta = {\left( {m - 3} \right)^2} - 4\left( { - m + 3} \right) > 0\\1 + \left( {m - 3} \right).1 - m + 3 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 6m + 9 + 4m - 12 > 0\\1 \ne 0\,\,\,\left( {luon\,\,dung} \right)\end{array} \right.\\ \Leftrightarrow {m^2} - 2m - 3 > 0\\ \Leftrightarrow \left[ \begin{array}{l}m > 3\\m < - 1\end{array} \right.\end{array}\) Kết hợp điều kiện bài toán ta suy ra \(m \in \left[ { - 2020; - 1} \right) \cup \left( {3;2020} \right]\), \(m \in \mathbb{Z}\). Vậy có 2019 + 2017 = 4036 giá trị của m thỏa mãn yêu cầu bài toán. Chọn A. Câu hỏi 20 : Cho hàm số \(y = {x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4\,\,\,\left( {{C_m}} \right)\). Giá trị của tham số \(m\) để đưởng thẳng \(\left( d \right):y = x + 4\) cắt \(\left( {{C_m}} \right)\) tại ba điểm phân biệt \(A\left( {0;4} \right),\,\,B,\,\,C\) sao cho tam giác \(KBC\) có diện tích bằng \(8\sqrt 2 \) với điểm \(K\left( {1;3} \right)\) là:
Đáp án: C Phương pháp giải: + Xét phương trình hoành độ giao điểm và tìm mối quan hệ giữa \({x_1},{x_2}\) là hoành độ của \(B,C\). + Viết công thức tính diện tích tam giác \(KBC\) và tìm \(m\). Lời giải chi tiết: + Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng ta có: \(\begin{array}{l}{x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4 = x + 4\\ \Leftrightarrow {x^3} + 2m{x^2} + \left( {m + 2} \right)x = 0\\ \Leftrightarrow x\left( {{x^2} + 2mx + m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + 2mx + m + 2 = 0\,\,\,\,\,\left( 1 \right)\end{array} \right.\end{array}\) Để \(\left( d \right)\) cắt \(\left( {{C_m}} \right)\) tại 3 điểm phân biệt thì phương trình \(\left( 1 \right)\) có 2 nghiệm phân biệt khác 0 \( \Rightarrow \left\{ \begin{array}{l}\Delta ; > 0\\0 + 2m.0 + m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - m - 2 > 0\\m \ne - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m \ne 2\end{array} \right.\) . Gọi \({x_1};\,\,{x_2}\) là \(2\) nghiệm phân biệt của phương trình \(\left( 1 \right)\) \( \Rightarrow B\left( {{x_1};{x_1} + 4} \right);\,\,\,C\left( {{x_2};{x_2} + 4} \right).\) Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m\\{x_1}.{x_2} = m + 2\end{array} \right..\) Ta có: \({S_{KBC}} = \frac{1}{2}.d\left( {K,BC} \right).BC.\) Phương trình đường thẳng \(\left( d \right):\,\,y = x + 4 \Leftrightarrow x - y + 4 = 0\). Vì \(B,\,\,C\) thuộc đường thẳng \(\left( d \right)\) nên ta có: \(d\left( {K,BC} \right) = d\left( {K;d} \right) = \frac{{\left| {1 - 3 + 4} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 .\) \(\begin{array}{l}BC = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_2} + 4 - {x_1} - 4} \right)}^2}} \\BC = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} \\BC = \sqrt 2 .\sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \\BC = \sqrt 2 .\sqrt {4{m^2} - 4\left( {m + 2} \right)} \\BC = 2\sqrt 2 .\sqrt {{m^2} - m - 2} \end{array}\) Theo bài ra ta có: \(\begin{array}{l}{S_{KBC}} = 8\sqrt 2 \\ \Leftrightarrow \frac{1}{2}.\sqrt 2 .2\sqrt 2 \sqrt {{m^2} - m - 2} = 8\sqrt 2 \\ \Leftrightarrow \sqrt {{m^2} - m - 2} = 4\sqrt 2 \\ \Leftrightarrow {m^2} - m - 2 = 32\\ \Leftrightarrow {m^2} - m - 34 = 0\\ \Leftrightarrow m = \frac{{1 \pm \sqrt {137} }}{2}\,\,\,\left( {tm} \right)\end{array}\) Vậy \(m = \frac{{1 \pm \sqrt {137} }}{2}\). Chọn C. Câu hỏi 21 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
Tìm tất cả các giá trị của \(m\) để bất phương trình \(f\left( {3 - {x^2}} \right) \ge m\) vô nghiệm?
Đáp án: D Phương pháp giải: - Đặt \(t = 3 - {x^2}\), đưa bất phương trình đã cho về dạng \(f\left( t \right) \le m\). - Tìm điều kiện cho ẩn \(t\), dựa vào BBT của hàm số \(f\left( x \right)\) để giải bài toán. Lời giải chi tiết: Đặt \(t = 3 - {x^2}\), ta có: \({x^2} \ge 0,\,\,\,\forall x \in \mathbb{R} \Rightarrow t = 3 - {x^2} \le 3,\,\,\,\,\forall x \in \mathbb{R}\)\( \Rightarrow t \in \left( { - \infty ;3} \right].\) Bất phương trình \(f\left( {3 - {x^2}} \right) \ge m\) vô nghiệm khi và chỉ khi \(f\left( t \right) \ge m\) vô nghiệm với mọi \(t \in \left( { - \infty ;3} \right].\) Từ BBT của hàm số \(y = f\left( x \right)\) ta thấy: \(f\left( t \right) \ge m\) vô nghiệm với \(t \in \left( { - \infty ;3} \right]\) khi \(m > 3\). Vậy \(m > 3\). Chọn D. Câu hỏi 22 : Hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
Số nghiệm của phương trình \(f\left( {{x^3} - 3x} \right) + 3{x^3} - 3x - 13 = {\left( {{x^2} - 2} \right)^3} - 3{\left( {x - 1} \right)^2}\) là:
Đáp án: C Phương pháp giải: Biến đổi, đưa phương trình về phương trình ẩn \(t = {x^3} - 3x\). Lời giải chi tiết: Ta có: \(f\left( {{x^3} - 3x} \right) + 3{x^3} - 3x - 13 = {\left( {{x^2} - 2} \right)^3} - 3{\left( {x - 1} \right)^2}\)\(\begin{array}{l} \Leftrightarrow f\left( {{x^3} - 3x} \right) + 3{x^3} - 3x - 13 = {x^6} - 6{x^4} + 12{x^2} - 8 - 3{x^2} + 6x - 3\\ \Leftrightarrow f\left( {{x^3} - 3x} \right) + 3{x^3} - 9x = {x^6} - 6{x^4} + 9{x^2} + 2 \Leftrightarrow f\left( {{x^3} - 3x} \right) = {\left( {{x^3} - 3x} \right)^2} - 3\left( {{x^3} - 3x} \right) + 2\,\,(*)\end{array}\) Đặt \(t = {x^3} - 3x,\,\,t \in \mathbb{R}\). Phương trình trở thành: \(g\left( t \right) = {t^2} - 3t + 2\). Biểu diễn đồ thị của hàm số \(y = g\left( x \right)\) :
Từ đồ thị hàm số, ta có: \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = 0\\{x^3} - 3x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = 0\\{x^3} - 3x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 3 \\x = - 1\\x = 2\end{array} \right.\) Số nghiệm của phương trình đã cho là: 5. Chọn C. Câu hỏi 23 : Cho đường cong \(\left( C \right):y = \dfrac{{x - 3}}{{x + 1}}\) và đường thẳng \(d:\,y = x + 3m\). Tìm tất cả các giá trị của \(m\) để \(d\) và \(\left( C \right)\) cắt nhau tại hai điểm phân biệt \(A,B\) sao cho trung điểm \(I\) của đoạn thẳng \(AB\) có hoành độ bằng 3.
Đáp án: B Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có hai nghiệm phân biệt. - Sử dụng hệ thức Vi-et. - Sử dụng công thức trung điểm: \(I\) là trung điểm của \(AB\) thì \({x_I} = \dfrac{{{x_A} + {x_B}}}{2}\) . Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{x - 3}}{{x + 1}} = x + 3m\,\,\left( {x \ne - 1} \right)\\ \Leftrightarrow x - 3 = {x^2} + 3mx + x + 3m\\ \Leftrightarrow {x^2} + 3mx + 3m + 3 = 0\,\,\,\left( * \right)\end{array}\) Để \(\left( C \right)\) và \(d\) cắt nhau tại hai điểm phân biệt thì phương trình (*) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta > 0 \Leftrightarrow 9{m^2} - 12m - 12 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - \dfrac{2}{3}\end{array} \right.\) Khi đó, phương trình (1) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn: \({x_1} + {x_2} = - 3m\) (Định lí Vi-ét). Trung điểm \(I\) của AB có hoành độ 3 nên: \(\dfrac{{{x_1} + {x_2}}}{2} = 3\)\( \Leftrightarrow \dfrac{{ - 3m}}{2} = 3 \Leftrightarrow m = - 2\,\,\,\left( {tm} \right).\) Chọn B. Câu hỏi 24 : Cho hàm số \(y = \dfrac{{x - 1}}{{x + 1}}\) có đồ thị \(\left( C \right)\). Biết đồ thị \(\left( C \right)\) cắt \(Ox,\,\,Oy\) lần lượt tại \(A,\,\,B\). Có bao nhiêu điểm \(M\) có tọa độ nguyên thuộc \(\left( C \right)\) sao cho \({S_{\Delta MAB}} = 3\).
Đáp án: B Phương pháp giải: Xác định tọa độ các điểm A, B. Sử dụng công thức tính diện tích tam giác sau để đánh giá tọa độ của điểm M: * Cho tam giác ABC, có tọa độ các vectơ \(\overrightarrow {AB} = \left( {{x_1};{y_1}} \right),\,\overrightarrow {AC} = \left( {{x_2};{y_2}} \right)\). Từ công thức diện tích: \({S_{ABC}} = \dfrac{1}{2}.AB.AC.\sin \widehat A\) ta chứng minh được công thức: \({S_{ABC}} = \dfrac{1}{2}.\left| {{x_1}{y_2} - {x_2}{y_1}} \right|\). Lời giải chi tiết: Tọa độ giao điểm của (C) với Ox, Oy lần lượt là \(A\left( {1;0} \right),\,B\left( {0; - 1} \right)\). Lấy \(M\left( {m;\dfrac{{m - 1}}{{m + 1}}} \right) \in \left( C \right),\,m \ne - 1\). Ta có: \(\overrightarrow {AB} = \left( { - 1; - 1} \right),\,\overrightarrow {AM} = \left( {m - 1;\dfrac{{m - 1}}{{m + 1}}} \right)\) Diện tích tam giác ABM: \({S_{ABM}} = \dfrac{1}{2}.\left| {\left( { - 1} \right).\dfrac{{m - 1}}{{m + 1}} - \left( { - 1} \right)\left( {m - 1} \right)} \right| = \dfrac{1}{2}.\left| {\dfrac{{m - {m^2}}}{{m + 1}}} \right| = 3\) \( \Rightarrow \left| {\dfrac{{m - {m^2}}}{{m + 1}}} \right| = 6 \Leftrightarrow \left[ \begin{array}{l}\dfrac{{m - {m^2}}}{{m + 1}} = 6\\\dfrac{{m - {m^2}}}{{m + 1}} = - 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m - {m^2} = 6m + 6\\m - {m^2} = - 6m - 6\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}{m^2} + 5m + 6 = 0\\{m^2} - 7m - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 2\\m = - 3\\m = \dfrac{{7 \pm \sqrt {73} }}{2} \notin \mathbb{Z}\end{array} \right.\) Vậy, có tất cả 2 giá trị nguyên của m thỏa mãn. Chọn B. Câu hỏi 25 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Tìm \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có nghiệm \(x \in \left( {0;\pi } \right)\).
Đáp án: C Phương pháp giải: Lời giải chi tiết: Với xÎ(0;p) thì \(\sin \,x \in \left( {0;1} \right]\). Xét hàm số \(f\left( x \right)\) trên nửa khoảng \(\left( {0;1} \right]\), ta có: Tập giá trị của \(f\left( x \right)\) trên nửa khoảng \(\left( {0;1} \right]\) là: \(\left[ { - 4; - 2} \right)\). Do đó, để phương trình f(sinx)=m có nghiệm xÎ(0;p) thì m Î [-4;-2). Chọn C. Câu hỏi 26 : Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{3}{2}\) là:
Đáp án: C Phương pháp giải: - Phá trị tuyệt đối, dựa vào đồ thị hàm số xác định giá trị của \({x^3} - 3x\). - Tiếp tục sử dụng bài toán tương giao. Lời giải chi tiết:
Quan sát đồ thị hàm số \(y = f\left( x \right)\), ta có: \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{3}{2}\)\( \Leftrightarrow \left[ \begin{array}{l}f\left( {{x^3} - 3x} \right) = \dfrac{3}{2}\\f\left( {{x^3} - 3x} \right) = - \dfrac{3}{2}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}{x^3} - 3x = a\,\,\,\left( {a < - 2} \right)\,\,\,\,\,\,\,\,\,(1)\\{x^3} - 3x = b\,\,\left( { - 2 < b < 0} \right)\,\,\,(2)\\{x^3} - 3x = c\,\,\left( {0 < c < 2} \right)\,\,\,\,\,\,(3)\\{x^3} - 3x = d\,\,\left( {d > 3} \right)\,\,\,\,\,\,\,\,\,\,\,\,(4)\end{array} \right.\) Quan sát đồ thị hàm số \(y = {x^3} - 3x\) bên: Ta có: Phương trình (1) có 1 nghiệm. Phương trình (2) có 3 nghiệm phân biệt. Phương trình (3) có 3 nghiệm phân biệt. Phương trình (4) có 1 nghiệm. Và các nghiệm của 4 phương trình trên là khác nhau. \( \Rightarrow \) Tổng số nghiệm của phương trình đã cho là: 1+3+3+1=8 Chọn C. Câu hỏi 27 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
Tìm tất cả các giá trị của m để phương trình \(\left| {f\left( x \right)} \right| + 1 = m\) có 4 nghiệm phân biệt
Đáp án: A Phương pháp giải: - Cách vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\). + Vẽ đồ thị hàm số \(y = f\left( x \right)\). + Lấy đối xứng phần đồ thị hàm số phía dưới trục \(Ox\) qua trục \(Ox\). + Xóa đi phần đồ thị hàm số phía dưới trục \(Ox\). - Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = m - 1\) là giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đườn thẳng \(y = m - 1\) có tính chất song song với trục hoành. Lời giải chi tiết: Ta có \(\left| {f\left( x \right)} \right| + 1 = m \Leftrightarrow \left| {f\left( x \right)} \right| = m - 1\)(*). Số nghiệm của phương trình (*) là giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đườn thẳng \(y = m - 1\) có tính chất song song với trục hoành. Từ đồ thị hàm số \(y = f\left( x \right)\) ta suy ra đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như sau:
Dựa vào đồ thị ta thấy phương trình (*) có 4 nghiệm phân biệt khi \(1 < m - 1 < 3 \Leftrightarrow 2 < m < 4.\) Chọn A. Câu hỏi 28 : Tìm tất cả các giá trị của m để phương trình \(m\sqrt {{x^2} + 2} = x + m\) có 2 nghiệm phân biệt
Đáp án: B Phương pháp giải: - Cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\). Khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\). - Lập BBT của hàm số \(y = f\left( x \right)\). - Dựa vào bảng biến thiên để xác định giá trị của m. Lời giải chi tiết: Ta có \(\begin{array}{l}\,\,\,\,\,\,\,\,m\sqrt {{x^2} + 2} = x + m\\ \Leftrightarrow m\left( {\sqrt {{x^2} + 2} - 1} \right) = x\\ \Leftrightarrow m = \dfrac{x}{{\sqrt {{x^2} + 2} - 1}} = f\left( x \right)\,\,\,\left( {x \in \mathbb{R}} \right)\\ \Rightarrow f'\left( x \right) = \dfrac{{2 - \sqrt {{x^2} + 2} }}{{{{\left( {\sqrt {{x^2} + 2} - 1} \right)}^2}}} = 0 \Leftrightarrow x = \pm \sqrt 2 \end{array}\) Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy để hàm số đã cho có 2 nghiệm thì \(\left[ \begin{array}{l} - \sqrt 2 < m < - 1\\1 < m < \sqrt 2 \end{array} \right.\). Chọn B. Câu hỏi 29 : Tìm điều kiện của \(m\) để đồ thị hàm số \(\left( {{C_m}} \right):y = {x^4} - m{x^2} + m - 1\) cắt trục hoành tại \(4\) điểm phân biệt.
Đáp án: B Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt \( \Leftrightarrow \) phương trình hoành độ giao điểm có 4 nghiệm phân biệt. - Giải điều kiện trên tìm \(m\). Lời giải chi tiết: Xét phương trình hoành độ giao điểm \({x^4} - m{x^2} + m - 1 = 0\). Đặt \(t = {x^2}\,\,\,\left( {t \ge 0} \right)\) ta được phương trình \({t^2} - mt + m - 1 = 0\). Để đồ thị hàm số \(\left( {{C_m}} \right):y = {x^4} - m{x^2} + m - 1\) cắt trục hoành tại 4 điểm phân biệt thì phương trình \({t^2} - mt + m - 1 = 0\) phải có hai nghiệm dương phân biệt. \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4m + 4 > 0\\m > 0\\m - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 2\\m > 1\end{array} \right.\) Chọn B. Câu hỏi 30 : PHẦN 2. TOÁN HỌC, TƯ DUY LOGIC, PHÂN TÍCH SỐ LIỆU Có bao nhiêu giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = {x^3} + \left( {m + 2} \right){x^2} + \left( {{m^2} - m - 3} \right)x - {m^2}\) cắt trục hoành tại \(3\) điểm phân biệt?
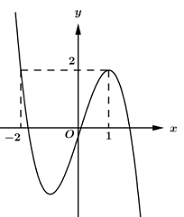
Đáp án: D Phương pháp giải: Đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại \(n\) điểm phân biệt với \(n\) là số nghiệm của phương trình \(f\left( x \right) = 0\) Lời giải chi tiết: \(\begin{array}{l}{x^3} + \left( {m + 2} \right){x^2} + \left( {{m^2} - m - 3} \right)x - {m^2} = 0\\ \Leftrightarrow \left( {x - 1} \right)\left[ {{x^2} + \left( {m + 3} \right)x + {m^2}} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} + \left( {m + 3} \right)x + {m^2} = 0{\rm{ }}\left( * \right)\end{array} \right.\end{array}\) Đồ thị hàm số cắt \(Ox\) tại \(3\) điểm phân biệt \( \Leftrightarrow \) Phương trình (*) có \(2\) nghiệm phân biệt khác \(1\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta = {\left( {m + 3} \right)^2} - 4{m^2} > 0\\{1^2} + \left( {m + 3} \right).1 + {m^2} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3{m^2} + 6m + 9 > 0\\{m^2} + m + 4 \ne 0\end{array} \right.\\ \Leftrightarrow {m^2} - 2m - 3 < 0\\ \Leftrightarrow - 1 < m < 3\end{array}\) Có \(3\) giá trị nguyên của \(m\) thỏa mãn Chọn D. Câu hỏi 31 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Tìm \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có đúng hai nghiệm trên đoạn \(\left[ {0;\pi } \right].\)
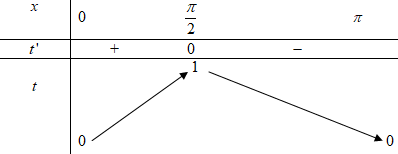
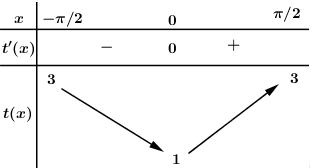
Đáp án: A Phương pháp giải: Sử dụng đồ thị. Lời giải chi tiết: Đặt \(\sin x = t \in \left[ {0;1} \right]\,\,\,\left( {do\,\,x \in \left[ {0;\pi } \right]} \right)\)\( \Rightarrow t' = \cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2}\) Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy ứng với mỗi giá trị của t khác 1 thì có 2 giá trị của x. Do đó để phương trình \(f\left( {\sin x} \right) = m\) có đúng 2 nghiệm trên đoạn \(\left[ {0;2} \right]\) thì phương trình \(f\left( t \right) = m\) phải có một nghiệm duy nhất trên \(\left[ {0;1} \right)\) \( \Rightarrow - 4 < m \le - 3.\) Chọn A. Câu hỏi 32 : Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để đường thẳng \(y = x + m - 1\) cắt đồ thị hàm số \(y = {x^3} + \left( {m - 3} \right){x^2} + x + 1\) tại ba điểm phân biệt \(A\left( {1;{y_A}} \right)\), \(B,\,\,\,C\) sao cho \(BC = 2\sqrt 3 \). Tổng bình phương tất cả các phần tử của tập hợp \(S\) là:
Đáp án: C Phương pháp giải: - Viết phương trình hoành độ giao điểm của đường thẳng và đồ thị hàm số. - Tìm điều kiện của \(m\) để phường trình hoành độ giao điểm có 3 nghiệm phân biệt. - Áp dụng định lí Vi – et để tìm mối liên hệ giữa các nghiệm của phương trình. Tìm giá trị của \(m\) thỏa mãn \(BC = 2\sqrt 3 \) Lời giải chi tiết: TXĐ : \(D = \mathbb{R}\) \(\begin{array}{l}d:\,\,\,\,\,\,y = x + m - 1\\\left( C \right):\,\,\,\,\,y = {x^3} + \left( {m - 3} \right){x^2} + x + 1\end{array}\) Phương trình hoành độ giao điểm của đường thẳng \(d\) và đồ thị \(\left( C \right)\) là : \(\begin{array}{l}x + m - 1 = {x^3} + \left( {m - 3} \right){x^2} + x + 1\,\,\,\,\left( 1 \right)\\ \Leftrightarrow {x^3} + \left( {m - 3} \right){x^2} - m + 2 = 0\\ \Leftrightarrow \left( {{x^3} - {x^2}} \right) + \left( {m - 2} \right){x^2} - \left( {m - 2} \right)x + \left( {m - 2} \right)x - \left( {m - 2} \right) = 0\end{array}\) \(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + \left( {m - 2} \right)x + m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} + \left( {m - 2} \right)x + m - 2 = 0\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\end{array}\) Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right)\) tại 3 điểm phân biệt khi phương trình (1) có 3 nghiệm phân biệt. Do đó, phương trình (2) phải có 2 nghiệm phân biệt và khác 1. Suy ra : \(\left\{ \begin{array}{l}\Delta > 0\\{1^2} + \left( {m - 2} \right).1 + m - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 2} \right)^2} - 4\left( {m - 2} \right) > 0\\2m - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 2} \right)\left( {m - 6} \right) > 0\\m \ne \dfrac{3}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 6\\\left\{ \begin{array}{l}m < 2\\m \ne \dfrac{3}{2}\end{array} \right.\end{array} \right.\,\,\,\,\,\left( * \right)\) Khi đó, phương trình (2) có 2 nghiệm phân biệt \({x_1};\,\,{x_2}\) thỏa mãn \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2 - m\\{x_1}.{x_2} = m - 2\end{array} \right.\) Suy ra \(B\left( {{x_1};\,{x_1} + m - 1} \right);\,\,\,C\left( {{x_2};\,\,{x_2} + m - 1} \right)\) Ta có: \(\begin{array}{l}BC = 2\sqrt 3 \\ \Leftrightarrow {\left( {{x_2} - {x_1}} \right)^2} + {\left[ {\left( {{x_2} + m - 1} \right) - \left( {{x_1} + m - 1} \right)} \right]^2} = {\left( {2\sqrt 3 } \right)^2}\\ \Leftrightarrow {\left( {{x_2} - {x_1}} \right)^2} + {\left( {{x_2} - {x_1}} \right)^2} = 12\\ \Leftrightarrow {\left( {{x_2} - {x_1}} \right)^2} = 6\end{array}\) \(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 6\\ \Leftrightarrow {\left( {2 - m} \right)^2} - 4\left( {m - 2} \right) = 6\\ \Leftrightarrow {m^2} - 4m + 4 - 4m + 8 = 6\\ \Leftrightarrow {m^2} - 8m + 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 4 + \sqrt {10} \\m = 4 - \sqrt {10} \end{array} \right.\left( {t/m\,\,\,\left( * \right)} \right) \Rightarrow S = \left\{ {4 + \sqrt {10} ;4 - \sqrt {10} } \right\}\end{array}\) Vậy tổng bình phương tất cả các phần tử của tập \(S\) bằng 52. Chọn C. Câu hỏi 33 : Biết rằng đường thẳng \(y = m - 3x\)cắt đồ thị \(\left( C \right):\,\,y = \dfrac{{2x - 1}}{{x - 1}}\) tại 2 điểm phân biệt \(A\)và \(B\) sao cho trọng tâm \(G\) của \(\Delta OAB\) thuộc đồ thị \(\left( C \right)\) với \(O\left( {0;0} \right)\) là gốc tọa độ. Khi đó giá trị thực của tham số \(m\)thuộc tập nào sao đây:
Đáp án: D Phương pháp giải: - Tìm ĐKXĐ. - Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có hai nghiệm phân biệt. - Sử dụng định lí Ví-ét: \({x_1} + {x_2} = - \dfrac{b}{a}\). - \(G\) là trọng tâm của \(\Delta OAB\) nên \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_O}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_O}}}{3}\end{array} \right.\). Tìm tọa độ điểm \(G\) theo \(m\). - Vì \(G \in \left( C \right)\) nên tọa độ điểm \(G\) thỏa mãn hàm số \(\left( C \right)\), thay tọa độ điểm \(G\) và giải phương trình tìm \(m\). Lời giải chi tiết: ĐKXĐ: \(x \ne 1\). Xét phương trình hoành độ giao điểm: \(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{2x - 1}}{{x - 1}} = m - 3x\,\,\left( {x \ne 1} \right)\\ \Leftrightarrow \left( {m - 3x} \right).\left( {x - 1} \right) = 2x - 1\\ \Leftrightarrow mx - m - 3{x^2} + 3x = 2x - 1\\ \Leftrightarrow - 3{x^2} + \left( {m + 1} \right)x - m + 1 = 0\,\,\,\left( * \right)\end{array}\) Để đường thẳng \(y = m - 3x\) cắt đồ thị \(\left( C \right)\) tại hai điểm phân biệt \(A,\,\,B\) thì phương trình (*) phải có 2 nghiệm phân biệt khác 1 \( \Leftrightarrow \Delta > 0\). \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 1} \right)^2} - 4.\left( { - 3} \right).\left( { - m + 1} \right) > 0\\ - 3 + m + 1 - m + 1 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 2m + 1 - 12m + 12 > 0\\ - 1 \ne 0\,\,\forall m\end{array} \right.\\ \Leftrightarrow {m^2} - 10m + 13 > 0\\ \Leftrightarrow \left[ \begin{array}{l}m > 5 + 2\sqrt 3 \\m < 5 - 2\sqrt 3 \end{array} \right.\end{array}\) Gọi \({x_A},\,\,{x_B}\) là hai nghiệm phân biệt của phương trình (*). Áp dụng định lí Vi-ét ta có: \({x_A} + {x_B} = \dfrac{{m + 1}}{3}\). Ta có: \(A,\,\,B\) thuộc đường thẳng \(y = m - 3x\) nên \(A\left( {{x_A};m - 3{x_A}} \right);\,\,B\left( {{x_B};m - 3{x_B}} \right)\). \(\begin{array}{l} \Rightarrow {y_A} + {y_B} = \left( {m - 3{x_A}} \right) + \left( {m - 3{x_B}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2m - 3\left( {{x_A} + {x_B}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2m - \left( {m + 1} \right) = m - 1\end{array}\) Theo bài ra ta có: \(G\) là trọng tâm của \(\Delta OAB\)nên: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_O}}}{3} = \dfrac{{m + 1}}{9}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_O}}}{3} = \dfrac{{m - 1}}{3}\end{array} \right.\) \( \Rightarrow G\left( {\dfrac{{m + 1}}{9};\dfrac{{m - 1}}{3}} \right)\). Để \(G \in \left( C \right)\) thì \(\dfrac{{m - 1}}{3} = \dfrac{{2.\dfrac{{m + 1}}{9} - 1}}{{\dfrac{{m + 1}}{9} - 1}}\) \(\begin{array}{l} \Rightarrow \dfrac{{m - 1}}{3} = \dfrac{{2m - 7}}{{m - 8}}\\ \Leftrightarrow {m^2} - 9m + 8 = 6m - 21\\ \Leftrightarrow {m^2} - 15m + 29 = 0\\ \Rightarrow \left[ \begin{array}{l}m = \dfrac{{15 - \sqrt {109} }}{2}\,\,\,\,\left( {ktm} \right)\\m = \dfrac{{15 + \sqrt {109} }}{2}\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(m = \dfrac{{15 + \sqrt {109} }}{2} \approx 12,72 \in \left( {3; + \infty } \right)\). Chọn D. Câu hỏi 34 : Với giá trị nào của \(m\) thì phương trình \(x + \sqrt {4 - {x^2}} = m\) có nghiệm:
Đáp án: D Phương pháp giải: Sử dụng bảng biến thiên Lời giải chi tiết: ĐKXĐ: \( - 2 \le x \le 2\). Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = x + \sqrt {4 - {x^2}} \) và đường thẳng \(y = m\). Xét hàm số \(y = x + \sqrt {4 - {x^2}} \) ta có: \(\begin{array}{l}y' = 1 - \dfrac{x}{{\sqrt {4 - {x^2}} }} = \dfrac{{\sqrt {4 - {x^2}} - x}}{{\sqrt {4 - {x^2}} }}\\y' = 0 \Leftrightarrow \sqrt {4 - {x^2}} - x \Leftrightarrow \sqrt {4 - {x^2}} = x\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\4 - {x^2} = {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = 2\end{array} \right. \Leftrightarrow x = \sqrt 2 \end{array}\) Bảng biến thiên:
Vậy phương trình \(x + \sqrt {4 - {x^2}} = m\) có nghiệm khi và chỉ khi \( - 2 \le m \le 2\sqrt 2 .\) Chọn D. Câu hỏi 35 : Cho phương trình \(\dfrac{{\left( {x - 2} \right)\left( {\left( {{m^2} - 1} \right)x + 1} \right)}}{{x - 1}} = 0\). Có tất cả bao nhiêu giá trị thực của m để phương trình có đúng một nghiệm ?
Đáp án: B Phương pháp giải: - Tìm ĐKXĐ. - \(\dfrac{{\left( {x - 2} \right)\left( {\left( {{m^2} - 1} \right)x + 1} \right)}}{{x - 1}} = 0 \Leftrightarrow \left( {x - 2} \right)\left( {\left( {{m^2} - 1} \right)x + 1} \right) = 0\). - Để phương trình \(\dfrac{{\left( {x - 2} \right)\left( {\left( {{m^2} - 1} \right)x + 1} \right)}}{{x - 1}} = 0\)có đúng một nghiệm thì phương trình \(\left( {{m^2} - 1} \right)x + 1 = 0\) hoặc vô nghiệm hoặc có nghiệm \(x = 2\) hoặc \(x = 1\). - Biện luận phương trình bậc nhất một ẩn \(ax + b = 0\). + Phương trình vô nghiệm \( \Leftrightarrow a = 0,\,\,b \ne 0\). + Phương trình có nghiệm duy nhất \( \Leftrightarrow a \ne 0\), khi đó \(x = - \dfrac{b}{a}\). Lời giải chi tiết: ĐKXĐ: \(x \ne 1\) \(\begin{array}{l}\,\,\,\,\,\,\dfrac{{\left( {x - 2} \right)\left( {\left( {{m^2} - 1} \right)x + 1} \right)}}{{x - 1}} = 0\,\,\,\,\,\,\,\left( 1 \right)\\ \Leftrightarrow \left( {x - 2} \right)\left( {\left( {{m^2} - 1} \right)x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\\left( {{m^2} - 1} \right)x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\,\,\left( {tm} \right)\\\left( {{m^2} - 1} \right)x = - 1\,\,\,\,\left( 2 \right)\end{array} \right.\end{array}\) Để phương trình (1) có đúng một nghiệm, ta có các trường hợp sau : TH1 : Phương trình (2) vô nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 1 = 0\\ - 1 \ne 0\end{array} \right. \Leftrightarrow m = \pm 1\) TH2 : Phương trình (2) có nghiệm \(x = 2\) hoặc \(x = 1\). \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 1 \ne 0\\\left[ \begin{array}{l}\dfrac{{ - 1}}{{{m^2} - 1}} = 1\\\dfrac{{ - 1}}{{{m^2} - 1}} = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \pm 1\\\left[ \begin{array}{l}{m^2} - 1 = - 1\\{m^2} - 1 = - \dfrac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \pm 1\\\left[ \begin{array}{l}m = 0\\m = \pm \dfrac{1}{{\sqrt 2 }}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = \pm \dfrac{1}{{\sqrt 2 }}\end{array} \right.\) Vậy có 5 giá trị của m thỏa mãn. Chọn B. Câu hỏi 36 : Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình sau
Số nghiệm của phương trình \(f\left( {\left| {2{\rm{cos}}\,x} \right|} \right) = 1\) với \(x \in \left( {0;\dfrac{{5\pi }}{2}} \right)\) là
Đáp án: C Phương pháp giải: Đặt \(2{\rm{cos}}\,x = t\), đánh giá nghiệm phương trình với ẩn t. Lời giải chi tiết: Đặt \(2{\rm{cos}}\,x = t\left( {t \in \left[ { - 2;2} \right]} \right)\). Phương trình \(f\left( {\left| {2{\rm{cos}}\,x} \right|} \right) = 1\) (1) trở thành \(f\left( {\left| t \right|} \right) = 1\) (2) Dựng đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) ta thấy, với \( - 2 \le x \le 2\) thì đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = 1\) tại 2 điểm \({x_0}\,,\,\, - {x_0}\,\,\left( {0 < {x_0} < 2} \right)\) Cho \(2{\rm{cos}}\,x = {x_0} \Rightarrow {\rm{cos}}\,x = \dfrac{{{x_0}}}{2} \in \left( {0;1} \right)\) \( \Rightarrow \) Phương trình có 3 nghiệm phân biệt \({x_1},{x_2},{x_3}\,\,\) \(\left( {0 < {x_1} < \dfrac{\pi }{2},\,\,\dfrac{{3\pi }}{2} < {x_2} < 2\pi < {x_3} < \dfrac{{5\pi }}{2}} \right)\) Cho \(2{\rm{cos}}\,x = - {x_0} \Rightarrow {\rm{cos}}\,x = - \dfrac{{{x_0}}}{2} \in \left( { - 1;0} \right)\) \( \Rightarrow \) Phương trình có 2 nghiệm phân biệt \({x_4},{x_5}\,\,\left( {\dfrac{\pi }{2} < {x_4} < \pi < {x_5} < \dfrac{{3\pi }}{2}} \right)\) Vậy số nghiệm của phương trình \(f\left( {\left| {2{\rm{cos}}\,x} \right|} \right) = 1\) với \(x \in \left( {0;\dfrac{{5\pi }}{2}} \right)\) là : \(5\). Chọn C. Câu hỏi 37 : Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên trên \(\mathbb{R}\) có đồ thị như hình vẽ. Số giá trị nguyên của tham số \(m\) để phương trình \(7.f\left( {5 - 2\sqrt {1 + 3\cos x} } \right) = 3m - 10\) có đúng hai nghiệm phân biệt thuộc \(\left[ { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right]\) là:
Đáp án: C Phương pháp giải: - Đặt ẩn phụ \(t = 5 - 2\sqrt {1 + 3\cos x} \), cô lập \(m\), đưa phương trình về dạng \(f\left( t \right) = m\). - Khảo sát hàm số \(t\left( x \right)\), tìm khoảng giá trị của \(t\) và xét xem ứng với mỗi giá trị \(t\) thuộc những khoảng nào thì cho bao nhiêu giá trị \(x\). - Dựa vào đồ thị hàm số \(f\left( t \right)\) trên khoảng tìm được, tìm điều kiện của \(m\) để phương trình ban đầu có đúng 2 nghiệm phân biệt. Lời giải chi tiết: Đặt \(t = 5 - 2\sqrt {1 + 3\cos x} \), phương trình trở thành \(7f\left( t \right) = 3m - 10 \Leftrightarrow f\left( t \right) = \dfrac{{3m - 10}}{7}\,\,\,\left( * \right)\). Ta có \(t'\left( x \right) = - 2.\dfrac{{ - 3\sin x}}{{2\sqrt {1 + 3\cos x} }} = \dfrac{{3\sin x}}{{\sqrt {1 + 3\cos x} }}\). Cho \(t'\left( x \right) = 0 \Leftrightarrow \sin x = 0 \Leftrightarrow x = k\pi \), mà \(x \in \left[ { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right]\) nên \(x = 0\). BBT: \( \Rightarrow t \in \left[ {1;3} \right]\) và với mỗi giá trị \(t \in \left( {1;3} \right]\) cho hai nghiệm \(x\), với \(t = 1\) cho 1 nghiệm \(x = 0\). Để phương trình ban đầu có 2 nghiệm phân biệt thuộc \(\left[ { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right]\) thì phương trình (*) có nghiệm duy nhất \(t \in \left( {1;3} \right]\) Xét hàm số \(f\left( t \right)\) trên \(\left( {1;3} \right]\), phương trình (*) có nghiệm duy nhất \( \Leftrightarrow \left[ \begin{array}{l} - 2 < \dfrac{{3m - 10}}{7} \le 0\\\dfrac{{3m - 10}}{7} = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - \dfrac{4}{3} < m \le \dfrac{{10}}{3}\\m = - 6\end{array} \right.\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1;2;3; - 6} \right\}\). Vậy có \(6\) giá trị của \(m\) thỏa mãn yêu cầu bài toán. Chọn C. Câu hỏi 38 : Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\) với \(a \ne 0\) có đồ thị như hình vẽ:
Phương trình \(\left| {f\left( {f\left( x \right)} \right)} \right| = m\) (với \(m\) là tham số thực), có tối đa bao nhiêu nghiệm?
Đáp án: C Phương pháp giải: Đặt \(f\left( x \right) = t\), phương trình trở thành \(\left| {f\left( t \right)} \right| = m\). Từ đồ thị hàm số \(y = f\left( t \right)\) ta suy ra đồ thị hàm số \(y = \left| {f\left( t \right)} \right|\) như sau: Lời giải chi tiết: Đặt \(f\left( x \right) = t\), phương trình trở thành \(\left| {f\left( t \right)} \right| = m\). Từ đồ thị hàm số \(y = f\left( t \right)\) ta suy ra đồ thị hàm số \(y = \left| {f\left( t \right)} \right|\) như sau:
Dựa vào đồ thị hàm số ta thấy phương trình \(\left| {f\left( t \right)} \right| = m\) có tối đa 6 nghiệm \(t > 0\). Lại có \(t = f\left( x \right)\), với mỗi \(t > 0\) thì mỗi phương trình cho 2 nghiệm \(x\). Vậy có tối đa 12 nghiệm \(x\). Chọn C. Câu hỏi 39 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên. Xác định số nghiệm của phương trình \(\left| {f\left( {{x^3} - 3{x^2}} \right)} \right| = \dfrac{3}{2},\) biết \(f\left( { - 4} \right) = 0.\)
Đáp án: C Phương pháp giải: Lời giải chi tiết: Đặt \(t = {x^3} - 3{x^2}\), phương trình trở thành \(\left| {f\left( t \right)} \right| = \frac{3}{2} \Leftrightarrow \left[ \begin{array}{l}f\left( t \right) = \frac{3}{2}\,\,\,\,\,\,\,\left( 1 \right)\\f\left( t \right) = - \frac{3}{2}\,\,\,\left( 2 \right)\end{array} \right.\). Dựa vào đồ thị hàm số ta thấy: + Phương trình (1) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}t = {x^3} - 3{x^2} = {t_1} \in \left( { - \infty ; - 4} \right)\\t = {x^3} - 3{x^2} = {t_2} \in \left( {2; + \infty } \right)\end{array} \right.\). + Phương trình (2) có 4 nghiệm phân biệt \(\left[ \begin{array}{l}t = {x^3} - 3{x^2} = {t_3} \in \left( { - 4; - 2} \right)\\t = {x^3} - 3{x^2} = {t_4} \in \left( { - 2;0} \right)\\t = {x^3} - 3{x^2} = {t_5} \in \left( {0;2} \right)\\t = {x^3} - 3{x^2} = {t_6} \in \left( {2; + \infty } \right) < {t_2}\end{array} \right.\). Ta có \(t' = 3{x^2} - 6x = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\). BBT:
Dựa vào BBT ta có: + Phương trình \({x^3} - 3{x^2} = {t_1} \in \left( { - \infty ; - 4} \right)\) có 1 nghiệm. + Phương trình \({x^3} - 3{x^2} = {t_2} \in \left( {2; + \infty } \right)\) có 1 nghiệm. + Phương trình \({x^3} - 3{x^2} = {t_3} \in \left( { - 4; - 2} \right)\) có 3 nghiệm. + Phương trình \({x^3} - 3{x^2} = {t_4} \in \left( { - 2;0} \right)\) có 3 nghiệm. + Phương trình \({x^3} - 3{x^2} = {t_5} \in \left( {0;2} \right)\) có 1 nghiệm. + Phương trình \({x^3} - 3{x^2} = {t_6} \in \left( {2; + \infty } \right)\) có 1 nghiệm. Vậy phương trình ban đầu có \(1 + 1 + 3 + 3 + 1 + 1 = 10\) nghiệm phân biệt. Chọn C. Câu hỏi 40 : Tìm \(m\) để đường thẳng \(y=mx+1\) cắt đồ thị hàm số \(y=\frac{x+1}{x-1}\) tại hai điểm thuộc hai nhánh của đồ thị.
Đáp án: B Phương pháp giải: Viết phương trình hoành độ giao điểm, biện luận tính chất nghiệm và áp dụng hệ thức Viet tìm tham số Lời giải chi tiết: Phương trình hoành độ giao điểm là: \(mx + 1 = \frac{{x + 1}}{{x - 1}} \Leftrightarrow \left\{ \begin{array}{l} Theo hệ thức Vi-et ta có: \(\left\{ \begin{align} & {{x}_{1}}+{{x}_{2}}=1 \\ & {{x}_{1}}{{x}_{2}}=\frac{-2}{m} \\ \end{align} \right..\) Đường thẳng \(y=mx+1\) cắt đồ thị hàm số \(y=\frac{x+1}{x-1}\) tại hai điểm thuộc hai nhánh của đồ thị \(\Leftrightarrow \)\(\left( 1 \right)\) có hai nghiệm phân biệt \({{x}_{1}}\), \({{x}_{2}}\) khác \(1\) thỏa mãn \(\left( {{x}_{1}}-1 \right)\left( {{x}_{2}}-1 \right)<0\) \( \Leftrightarrow \left\{ \begin{array}{l} Chọn B
|