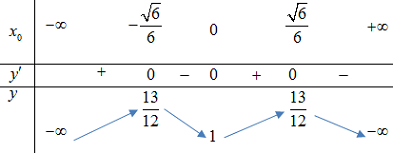Phương pháp giải:

Phương trình tiếp tuyến của hàm số \(y=f\left( x \right)\) tại điểm \({{x}_{0}}\) là \(y-f\left( {{x}_{0}} \right)=f'\left( x{{}_{0}} \right)\left( x-{{x}_{0}} \right).\)

Viết phương trình tiếp tuyến sau đó tìm hoành độ giao điểm của phương trình tiếp tuyến với đồ thị hàm số để tìm giao điểm thứ \(2.\)

Lời giải chi tiết:

Ta có \(y'=3{{x}^{2}}-3\Rightarrow y'\left( 1 \right)=0.\) Do đó tiếp tuyến tại \(N\left( 1;1 \right)\) có dạng \(y-1=y'\left( 1 \right)\left( x-1 \right)\Leftrightarrow d:y=1.\) Khi đó \(d\cap \left( C \right)\) có hoành độ giao điểm là \({x^3} - 3x + 3 = 1 \Leftrightarrow {x^3} - 3x + 2 = 0 \Leftrightarrow {\left( {x - 1} \right)^2}\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 2.\end{array} \right.\)

Giao điểm thứ \(2\) của \(d\) và \(\left( C \right)\) là \(M\left( -2;1 \right).\)

Chọn đáp án C.

Phương pháp giải:

- Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm thuộc đồ thị hàm số, viết phương trình tiếp tuyến của đồ thị hàm số tại \(M\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\,\,\,\left( d \right)\).

- Xác định tọa độ các điểm \(A = Ox \cap d,\,\,B = Oy \cap d\).

- Giải phương trình \(OA = OB\) tìm \({x_0}\), từ đó suy ra các phương trình tiếp tuyến thỏa mãn.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\). Ta có \(y' = \dfrac{{ - 4}}{{{{\left( {x - 1} \right)}^2}}}\).

Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm thuộc đồ thị hàm số, phương trình tiếp tuyến của đồ thị hàm số tại \(M\) là:

\(y = \dfrac{{ - 4}}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + \dfrac{{{x_0} + 3}}{{{x_0} - 1}}\,\,\,\left( d \right)\)

Gọi \(A = d \cap Ox\).

Cho \(y = 0\)

\(\begin{array}{l} \Rightarrow 0 = \dfrac{{ - 4}}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + \dfrac{{{x_0} + 3}}{{{x_0} - 1}}\\ \Leftrightarrow 0 =  - 4\left( {x - {x_0}} \right) + \left( {{x_0} + 3} \right)\left( {{x_0} - 1} \right)\\ \Leftrightarrow 0 =  - 4x + 4{x_0} + x_0^2 + 2{x_0} - 3\\ \Leftrightarrow x = \dfrac{{x_0^2 + 6{x_0} - 3}}{4}\end{array}\)

\( \Rightarrow A\left( {\dfrac{{x_0^2 + 6{x_0} - 3}}{4};0} \right)\) \( \Rightarrow OA = \dfrac{{\left| {x_0^2 + 6{x_0} - 3} \right|}}{4}\).

Gọi \(B = d \cap Oy\).

Cho \(x = 0\).

\(\begin{array}{l} \Rightarrow y = \dfrac{{4{x_0}}}{{{{\left( {{x_0} - 1} \right)}^2}}} + \dfrac{{{x_0} + 3}}{{{x_0} - 1}} = \dfrac{{4{x_0} + \left( {{x_0} + 3} \right)\left( {{x_0} - 1} \right)}}{{{{\left( {{x_0} - 1} \right)}^2}}}\\\,\,\,\,\,\,\,\,\, = \dfrac{{4{x_0} + x_0^2 + 2{x_0} - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}} = \dfrac{{x_0^2 + 6{x_0} - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}}\end{array}\)

\( \Rightarrow B\left( {0;\dfrac{{x_0^2 + 6{x_0} - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}}} \right) \Rightarrow OB = \dfrac{{\left| {x_0^2 + 6{x_0} - 3} \right|}}{{{{\left( {{x_0} - 1} \right)}^2}}}\).

Vì tam giác \(OAB\) vuông cân tại \(O\) nên \(OA = OB\).

\(\begin{array}{l} \Leftrightarrow \dfrac{{\left| {x_0^2 + 6{x_0} - 3} \right|}}{4} = \dfrac{{\left| {x_0^2 + 6{x_0} - 3} \right|}}{{{{\left( {{x_0} - 1} \right)}^2}}}\\ \Leftrightarrow \left| {x_0^2 + 6{x_0} - 3} \right|\left( {\dfrac{1}{4} - \dfrac{1}{{{{\left( {{x_0} - 1} \right)}^2}}}} \right) = 0\\ \Leftrightarrow \dfrac{1}{4} - \dfrac{1}{{{{\left( {{x_0} - 1} \right)}^2}}} = 0\end{array}\)  

(Do \(A \ne B\) nên \(x_0^2 + 6{x_0} - 3 \ne 0\))

\( \Leftrightarrow {\left( {{x_0} - 1} \right)^2} = 4 \Leftrightarrow \left[ \begin{array}{l}{x_0} - 1 = 2\\{x_0} - 1 =  - 2\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}{x_0} = 3\\{x_0} =  - 1\end{array} \right.\,\,\left( {tm} \right)\).

Với \({x_0} = 3\) \( \Rightarrow \) Phương trình tiếp tuyến: \(y =  - 1\left( {x - 3} \right) + 3 \Leftrightarrow y =  - x + 6\).

Với \({x_0} =  - 1\) \( \Rightarrow \) Phương trình tiếp tuyến: \(y =  - 1\left( {x + 1} \right) - 1 \Leftrightarrow y =  - x - 2\).

Chọn A.

Phương pháp giải:

- Gọi \(M\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số. Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(M\) là \(k = y'\left( {{x_0}} \right)\).

- Xét dấu tam thức bậc hai: \(a{x^2} + bx + c > 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  < 0\end{array} \right.\).

Lời giải chi tiết:

Gọi \(M\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số.

Ta có \(y' = 3{x^2} - 2\left( {m - 1} \right)x + m - 1\).

Suy ra hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm \(M\) là \(k = y'\left( {{x_0}} \right) = 3x_0^2 - 2\left( {m - 1} \right){x_0} + m - 1\).

Theo bài ra ta có:

\(\begin{array}{l}k > 0\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow 3x_0^2 - 2\left( {m - 1} \right){x_0} + m - 1 > 0\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}3 > 0\,\,\left( {luon\,\,dung} \right)\\\Delta ' = {\left( {m - 1} \right)^2} - 3\left( {m - 1} \right) < 0\,\end{array} \right.\,\forall x \in \mathbb{R}\\ \Leftrightarrow {m^2} - 2m + 1 - 3m + 3 < 0\\ \Leftrightarrow {m^2} - 5m + 4 < 0\\ \Leftrightarrow 1 < m < 4\end{array}\)

Mà \(m \in \mathbb{Z} \Rightarrow S = \left\{ {2;3} \right\}\).

Vậy tập hợp \(S\) có 2 phần tử.

Chọn D.

Phương pháp giải:

- Gọi tiếp điểm là \({A_0}\left( {{x_0};{y_0}} \right)\). Viết phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(A\left( {{x_0};{y_0}} \right)\)là: \(y = f'\left( {{x_0}} \right).\left( {x - {x_0}} \right) + {y_0}\).

- Cho tiếp tuyến vừa viết được đi qua \(M\left( { - 1; - 9} \right)\), giải phương trình tìm \({x_0}\).

- Số tiếp tuyến cần tìm là số nghiệm \({x_0}\) tìm được.

Lời giải chi tiết:

Gọi tiếp điểm là \({A_0}\left( {{x_0};{y_0}} \right)\). Ta có: \({y_0} = 4x_0^3 - 6x_0^2 + 1\)

Ta có: \(y' = 12{x^2} - 12x \Rightarrow y'\left( {{x_0}} \right) = 12x_0^2 - 12{x_0}\)

Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \({M_0}\left( {{x_0};{y_0}} \right)\)là:

\(y = \left( {12x_0^2 - 12{x_0}} \right).\left( {x - {x_0}} \right) + 4x_0^3 - 6x_0^2 + 1\) (d)

Theo bài ra ta có: \(M\left( { - 1; - 9} \right) \in d \Rightarrow \)\( - 9 = \left( {12x_0^2 - 12{x_0}} \right).\left( { - 1 - {x_0}} \right) + 4x_0^3 - 6x_0^2 + 1\).

\(\begin{array}{l} \Leftrightarrow  - 9 =  - 12x_0^2 - 12x_0^3 + 12{x_0} + 12x_0^2 + 4x_0^3 - 6x_0^2 + 1\\ \Leftrightarrow 8x_0^3 + 6x_0^2 - 12{x_0} - 10 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} =  - 1\\{x_0} = \dfrac{5}{4}\end{array} \right.\end{array}\)

Dễ dàng kiểm tra, mỗi giá trị \({x_0}\) tìm được cho ta đúng một phương trình tiếp tuyến, hai đường tiếp tuyến tìm được là phân biệt.

Vậy qua \(M\left( { - 1; - 9} \right)\) kẻ được hai tiếp tuyến đến đồ thị hàm số.

Chọn B.

Phương pháp giải:

- Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(x = a\) có phương trình là: \(y = f'\left( a \right)\left( {x - a} \right) + f\left( a \right).\) .

- Tính \(f\left( { - 2} \right)\) và đạo hàm của hàm số \(y = g\left( x \right)\) để tính \(g'\left( { - 2} \right).\)

Lời giải chi tiết:

Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(x =  - 2\) là:

      \(\begin{array}{l}y = f'\left( { - 2} \right).\left( {x + 2} \right) + f\left( { - 2} \right)\\ \Leftrightarrow 3x + 4 = 3.\left( {x + 2} \right) + f\left( { - 2} \right)\\ \Rightarrow f\left( { - 2} \right) =  - 2\end{array}\)

Ta có:

      \(\begin{array}{l}g\left( x \right) = {\left[ {f\left( x \right)} \right]^2} \Rightarrow g'\left( x \right) = 2.f'\left( x \right).f\left( x \right)\\ \Rightarrow g'\left( { - 2} \right) = 2.f'\left( { - 2} \right).f\left( { - 2} \right) = 2.3.\left( { - 2} \right) =  - 12.\end{array}\)

Vậy \(g'\left( { - 2} \right) =  - 12.\)

Chọn B.

Phương pháp giải:

Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(M\left( {{x_0};{y_0}} \right)\)là: \(y = f'\left( {{x_0}} \right).\left( {x - {x_0}} \right) + {y_0}\).

Lời giải chi tiết:

Đồ thị hàm số \(y = \dfrac{{4x - 3}}{{2x + 1}}\) \(\left( C \right)\) có hai tiệm cận là: \(x =  - \dfrac{1}{2},\,y = 2\), giao điểm của hai tiệm cận là: \(I\left( { - \dfrac{1}{2};2} \right)\)

Lấy \(M\left( {{x_0};{y_0}} \right) \in \left( C \right) \Rightarrow {y_0} = \dfrac{{4{x_0} - 3}}{{2{x_0} + 1}}\,\,\left( {{x_0} \ne  - \dfrac{1}{2}} \right)\), \(y'\left( {{x_0}} \right) = \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}\)

PTTT của \(\left( C \right)\) tại điểm M là: \(y = \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( {x - {x_0}} \right) + \dfrac{{4{x_0} - 3}}{{2{x_0} + 1}}\,\,\left( d \right)\)

Cho \(x =  - \dfrac{1}{2} \Rightarrow \)\(y = \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( { - \dfrac{1}{2} - {x_0}} \right) + \dfrac{{4{x_0} - 3}}{{2{x_0} + 1}}\)\( = \dfrac{{ - 5}}{{2{x_0} + 1}} + \dfrac{{4{x_0} - 3}}{{2{x_0} + 1}} = \dfrac{{4{x_0} - 8}}{{2{x_0} + 1}}.\) 

\( \Rightarrow \)Giao điểm của d và TCĐ của \(\left( C \right)\) là: \(A\left( { - \dfrac{1}{2};\dfrac{{4{x_0} - 8}}{{2{x_0} + 1}}} \right)\)\( \Rightarrow IA = \left| {\dfrac{{4{x_0} - 8}}{{2{x_0} + 1}} - 2} \right| = \left| {\dfrac{{10}}{{2{x_0} + 1}}} \right|.\)

Cho \(y = 2\) ta có:

\(\begin{array}{l}2 = \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( {x - {x_0}} \right) + \dfrac{{4{x_0} - 3}}{{2{x_0} + 1}}\\ \Leftrightarrow \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( {x - {x_0}} \right) = \dfrac{5}{{2{x_0} + 1}}\\ \Leftrightarrow x - {x_0} = \dfrac{{2{x_0} + 1}}{2} \Leftrightarrow x = \dfrac{{4{x_0} + 1}}{2}\end{array}\)

\( \Rightarrow \) Giao điểm của d và TCN của \(\left( C \right)\) là: \(B\left( {\dfrac{{4{x_0} + 1}}{2};2} \right)\)\( \Rightarrow IB = \left| {\dfrac{{4{x_0} + 1}}{2} + \dfrac{1}{2}} \right| = \left| {2{x_0} + 1} \right|.\)

Diện tích tam giác tạo thành là: \(S = \dfrac{1}{2}.IA.IB = \dfrac{1}{2}.\left| {\dfrac{{10}}{{2{x_0} + 1}}} \right|.\left| {2{x_0} + 1} \right| = 5\).

Chọn C.

Phương pháp giải:

- Giả sử hoành độ của \(A,\,\,B\) lần lượt là \(a,\,\,b\,\,\left( {a \ne b} \right)\). Dựa vào giả thiết tiếp tuyến của \(\left( C \right)\) tại \(A,\,\,B\) song song với nhau, tức là \(y'\left( a \right) = y'\left( b \right)\), rút \(b\) theo \(a\).

- Viết phương trình tiếp tuyến tại \(A,\,\,B\) theo tham số \(a\).

- Xác định tọa độ các điểm \(E,\,\,F\) theo tham số \(a\).

- Tính \(EF\) theo tham số \(a\), sử dụng giả thiết \(EF \le 2020\) tìm khoảng giá trị của \(a\), từ đó tìm những số nguyên dương \(a\) thỏa mãn điều kiện tìm được.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\). Ta có: \(y' = 3{x^2} - 3\).

Giả sử hoành độ của \(A,\,\,B\) lần lượt là \(a,\,\,b\,\,\left( {a \ne b} \right)\). Do tiếp tuyến của \(\left( C \right)\) tại \(A,\,\,B\) song song với nhau nên

\(y'\left( a \right) = y'\left( b \right) \Leftrightarrow 3{a^2} - 3 = 3{b^2} - 3 \Leftrightarrow \left[ \begin{array}{l}a = b\,\,\,\,\,\left( {ktm} \right)\\a =  - b\end{array} \right.\)

Ta có:  \(A\left( {a;{a^3} - 3a + 1} \right),\,B\left( { - a; - {a^3} + 3a + 1} \right)\) (\(a \in {\mathbb{N}^*}\)).

+) Tiếp tuyến của \(\left( C \right)\) tại \(A\) có phương trình:

\(y = \left( {3{a^2} - 3} \right)\left( {x - a} \right) + {a^3} - 3a + 1 \Leftrightarrow y = \left( {3{a^2} - 3} \right)x - 2{a^3} + 1\)

Giao điểm của tiếp tuyến này với \(Oy\)là điểm \(E\left( {0; - 2{a^3} + 1} \right)\).

+) Tiếp tuyến của \(\left( C \right)\) tại \(B\) có phương trình:

\(y = \left( {3{a^2} - 3} \right)\left( {x + a} \right) - {a^3} + 3a + 1 \Leftrightarrow y = \left( {3{a^2} - 3} \right)x + 2{a^3} + 1\)

Giao điểm của tiếp tuyến này với \(Oy\) là điểm \(F\left( {0;2{a^3} + 1} \right)\).

\( \Rightarrow EF = \left| {4{a^3}} \right| = 4{a^3}\,\, \Rightarrow 4{a^3} < 2020\, \Rightarrow a < \sqrt[3]{{505}} \approx 7,96\)

Mà \(a \in {\mathbb{N}^*}\)\( \Rightarrow a \in \left\{ {1;2;...;7} \right\}\).

Vậy có 7 giá trị của \(a\) thỏa mãn yêu cầu bài toán.

Chọn D.

Phương pháp giải:

- Tìm 2 đường tiệm cận của đồ thị hàm số.

- Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số. Viết phương trình tiếp tuyến của đồ thị hàm số tại \(M\).

- Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).

- Tìm giao điểm \(A,\,\,B\) của tiếp tuyến với 2 đường tiệm cận.

- Tính độ dài đoạn thẳng \(AB:\) \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).

- Giải phương trình tìm \(m\), từ đó tính \(S\).

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\). Đồ thị hàm số có hai đường tiệm cận là \(x = 2\) và \(y = 2\).

Ta có \(y' = \dfrac{{ - 2}}{{{{\left( {x - 2} \right)}^2}}}\). Gọi \(M\left( {m;\,\dfrac{{2m - 2}}{{m - 2}}} \right)\) thuộc đồ thị hàm số.

Phương trình tiếp tuyến \(d\) của \(\left( C \right)\) tại \(M\): \(y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\).

Cho \(x = 2 \Rightarrow y = \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {2 - m} \right) + \dfrac{{2m - 2}}{{m - 2}}\)\( \Leftrightarrow y = \dfrac{2}{{m - 2}} + \dfrac{{2m - 2}}{{m - 2}} = \dfrac{{2m}}{{m - 2}}\).

\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(x = 2\) là \(A\left( {2;\,\dfrac{{2m}}{{m - 2}}} \right)\).

Cho \(y = 2 \Rightarrow \dfrac{{ - 2}}{{{{\left( {m - 2} \right)}^2}}}\left( {x - m} \right) + \dfrac{{2m - 2}}{{m - 2}} = 2\).

\(\begin{array}{l} \Leftrightarrow  - 2\left( {x - m} \right) + \left( {2m - 2} \right)\left( {m - 2} \right) = 2{\left( {m - 2} \right)^2}\\ \Leftrightarrow  - 2x + 2m + 2{m^2} - 6m + 4 = 2{m^2} - 8m + 8\\ \Leftrightarrow 2x = 4m - 4 \Leftrightarrow x = 2m - 2\end{array}\)

\( \Rightarrow \) Giao điểm của \(d\) và đường thẳng \(y = 2\) là \(B\left( {2m - 2;\,2} \right)\).

Ta có: \(AB = 2\sqrt 5  \Leftrightarrow {\left( {2m - 4} \right)^2} + {\left( {2 - \dfrac{{2m}}{{m - 2}}} \right)^2} = 20\)

\(\begin{array}{l} \Leftrightarrow 4{\left( {m - 2} \right)^2} + \dfrac{{16}}{{{{\left( {m - 2} \right)}^2}}} = 20\\ \Leftrightarrow {\left( {m - 2} \right)^4} - 5{\left( {m - 2} \right)^2} + 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{\left( {m - 2} \right)^2} = 1\\{\left( {m - 2} \right)^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = 1\\m = 4\\m = 0\end{array} \right.\end{array}\)

Vậy \(S = 3 + 1 + 4 + 0 = 8\).

Chọn C.

Phương pháp giải:

- Tiếp tuyến của đồ thị hàm số tại \(A\left( {1;\,\, - 2} \right)\) song song với đường thẳng \(d:\,\,3x + y - 4 = 0\) nên \(y'\left( 1 \right) =  - 3\).

- Điểm \(A\left( {1; - 2} \right)\) thuộc đồ thị hàm số nên thay điểm \(A\) vào hàm số.

- Giải hệ 2 phương trình bằng phương pháp thế, tìm \(a,\,\,b\) và tính \(a - 3b\).

Lời giải chi tiết:

Ta có \(y' = \dfrac{{ - 2 - ab}}{{{{\left( {ax - 2} \right)}^2}}} \Rightarrow y'\left( 1 \right) = \dfrac{{ - 2 - ab}}{{{{\left( {a - 2} \right)}^2}}}\).

Do tiếp tuyến song song với đường thẳng \(d:\,\,3x + y - 4 = 0\) nên: \(y'\left( 1 \right) =  - 3 \Leftrightarrow \dfrac{{ - 2 - ab}}{{{{\left( {a - 2} \right)}^2}}} =  - 3\).

Mặt khác \(A\left( {1; - 2} \right)\) thuộc đồ thị hàm số nên \( - 2 = \dfrac{{1 + b}}{{a - 2}}\)\( \Leftrightarrow b =  - 2a + 3\).

Khi đó ta có :

\(\begin{array}{l}\dfrac{{ - 2 - ab}}{{{{\left( {a - 2} \right)}^2}}} =  - 3 \Leftrightarrow  - 2 - a\left( { - 2a + 3} \right) =  - 3{a^2} + 12a - 12\,\,\left( {a \ne 2} \right)\\ \Leftrightarrow 5{a^2} - 15a + 10 = 0 \Leftrightarrow \left[ \begin{array}{l}a = 2\,\,\,\,\left( {ktm} \right)\\a = 1\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\).

Với \(a = 1 \Rightarrow b = 1 \Rightarrow a - 3b =  - 2\).

Chọn A.

Phương pháp giải:

- Gọi \(A\left( {m;0} \right) = d \cap Ox\,\,\left( {m \ne 0} \right)\), xác định tọa độ điểm \(B\) theo \(m\).

- Viết phương trình đoạn chắn của đường thẳng \(d\) đi qua \(A,\,\,B\).

- \(\left( d \right):\,\,y = ax + b\) tiếp xúc với đồ thị hàm số \(y = f\left( x \right)\) thì \(a = f'\left( x \right)\). Tìm \(x\) và viết phương trình tiếp tuyến sau đó suy ra \(a,\,\,b\).

Lời giải chi tiết:

Gọi \(A\left( {m;0} \right) = d \cap Ox\,\,\left( {m \ne 0} \right)\) \( \Rightarrow OA = \left| m \right|\).

\( \Rightarrow OB = 9OA = 9\left| m \right|\)\( \Rightarrow B\left( {0;9\left| m \right|} \right) = d \cap Oy\).

Khi đó ta có phương trình đoạn chắn của đường thẳng \(d\) là:

\(\dfrac{x}{m} + \dfrac{y}{{9\left| m \right|}} = 1 \Leftrightarrow y =  - \dfrac{{9\left| m \right|}}{m}x + 9\left| m \right|\).

\( \Rightarrow a =  - \dfrac{{9\left| m \right|}}{m} =  \pm 9\), \(b = 9\left| m \right|\).

Vì \(d\) là tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) nên \(y' = 3{x^2} - 6x =  \pm 9 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right.\).

Theo giả thiết \(d\) là tiếp tuyến của \(\left( C \right)\) tại điểm có hoành độ dương nên \(d\) là tiếp tuyến tại điểm có hoành độ \(x = 3\).

\( \Rightarrow y'\left( 3 \right) = 9;\,\,y\left( 3 \right) = 2\).

Suy ra phương trình đường thẳng \(d\) là \(y = 9\left( {x - 3} \right) = 2 \Leftrightarrow 9x - 25\).

Vậy \(a = 9;\,\,b =  - 25 \Rightarrow a - b = 34\).

Chọn B.

Phương pháp giải:

Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(k = y'\left( {{x_0}} \right)\).

Lời giải chi tiết:

\(y = {x^4} - 2{x^2} \Rightarrow y' = 4{x^3} - 4x\).

Giả sử các tiếp tuyến tại \(A,\,\,B,\,\,C\) có hệ số góc cùng bằng \(k \Rightarrow 4{x^3} - 4x = k\,\,\,\left( 1 \right)\).

Ta có: \({x^4} - 2{x^2} = \frac{1}{4}x\left( {4{x^3} - 4x} \right) - {x^2} = \frac{1}{4}xk - {x^2}\).

Do đó ba điểm \(A,\,\,B,\,\,C\) thuộc đồ thị hàm số \(y =  - {x^2} + \frac{1}{4}kx\,\,\left( P \right)\).

Theo giả thiết \(\left( P \right)\) có đỉnh \(I\left( {\frac{1}{6};{y_0}} \right)\) nên \(\frac{{ - \frac{1}{4}k}}{{2\left( { - 1} \right)}} = \frac{1}{6} \Leftrightarrow  - \frac{1}{4}k =  - \frac{1}{3} \Leftrightarrow k = \frac{4}{3}\).

Khi đó \(\left( P \right):\,\,y =  - {x^2} + \frac{1}{3}x\).

Vậy \({y_0} = y\left( {\frac{1}{6}} \right) =  - {\left( {\frac{1}{6}} \right)^2} + \frac{1}{3}.\frac{1}{6} = \frac{1}{{36}}\).

Chọn B.

Phương pháp giải:

- Tìm điểm cố định mà với mọi giá trị của \(m\) thì đồ thị hàm số luôn đi qua.

- Viết phương trình tiếp tuyến tại điểm đó.

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,y = {x^4} + \left( {m - 2} \right){x^2} - 2\left( {m + 2} \right)x + m + 5\\ \Leftrightarrow y = \left( {{x^4} - 2{x^2} - 4x + 5} \right) + m\left( {{x^2} - 2x + 1} \right)\end{array}\)

Để \(\left( {{C_m}} \right)\) luôn đi qua 1 điểm khi \(m\) thay đổi thì \({x^2} - 2x + 1 = 0 \Leftrightarrow x = 1\)

Với \(x = 1\) thì \(y = 0\), suy ra đồ thị hàm số \(\left( {{C_m}} \right)\) luôn đi qua điểm cố định \(A\left( {1;0} \right)\).

Ta có: \(y' = f'\left( x \right) = 4{x^3} + 2\left( {m - 2} \right)x - 2\left( {m + 2} \right)\).

\( \Rightarrow f'\left( 1 \right) = 4 + 2.\left( {m - 2} \right).1 - 2\left( {m + 2} \right) = 4 + 2m - 4 - 2m - 4 =  - 4\)

Suy ra phương trình tiếp tuyến chung của các đường cong \(\left( {{C_m}} \right)\) tại điểm \(A\left( {1;0} \right)\) là:

\(d:y = f'\left( 1 \right)\left( {x - 1} \right) + 0 =  - 4\left( {x - 1} \right) =  - 4x + 4.\)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

\(\left( C \right):\,\,y =  - {x^3} + 3{x^2} - 2 \Rightarrow y' =  - 3{x^2} + 6x\)

Tiếp tuyến của \(\left( C \right)\) song song với đường thẳng \(d:\,\,y =  - 9x - 7\).

\( \Leftrightarrow \) Hệ số góc của tiếp tuyến bằng \( - 9\).

\( \Leftrightarrow y'\left( {{x_0}} \right) =  - 9 \Leftrightarrow  - 3x_0^2 + 6{x_0} =  - 9 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 3 \Rightarrow {y_0} =  - 2\\{x_0} =  - 1 \Rightarrow {y_0} = 2\end{array} \right.\).

+ Tại tiếp điểm \(\left( {3; - 2} \right) \Rightarrow \) Phương trình tiếp tuyến là: \(y =  - 9\left( {x - 3} \right) - 2 =  - 9x + 25\).

+ Tại tiếp điểm \(\left( { - 1;2} \right) \Rightarrow \) Phương trình tiếp tuyến là: \(y =  - 9\left( {x + 1} \right) + 2 =  - 9x - 7\) (loại vì trùng \(d\)).

Chọn B

Phương pháp giải:

Lời giải chi tiết:

Lập phương trình đường thẳng đi qua \(M\left( {1;3} \right)\):

\(y = k\left( {x - {x_0}} \right) + {y_0} \Leftrightarrow y = k\left( {x - 1} \right) + 3\)

Để đường thẳng đi qua \(M\left( {1;3} \right)\) tiếp xúc với đồ thị \(\left( C \right)\):

\( \Rightarrow \left\{ \begin{array}{l}{x^4} + 2{x^2} = k\left( {x - 1} \right) + 3\,\,\,\,\,\,\,\,\,\left( 1 \right)\\4{x^3} + 4x = k\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Thế (2) vào (1) ta có:

\(\begin{array}{l}{x^4} + 2{x^2} = \left( {4{x^3} + 4x} \right)\left( {x - 1} \right) + 3 \Leftrightarrow {x^4} + 2{x^2} = 4{x^4} - 4{x^3} + 4{x^2} - 4x + 3\\ \Leftrightarrow 3{x^4} - 4{x^3} + 2{x^2} - 4x + 3 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {3{x^3} - {x^2} + x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\3{x^3} - {x^2} + x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\3\left( {{x^3} - 1} \right) - x\left( {x - 1} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\3\left( {x - 1} \right)\left( {{x^2} - x + 1} \right) - x\left( {x - 1} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\\left( {x - 1} \right)\left( {3{x^2} - 4x + 3} \right) = 0\end{array} \right. \Leftrightarrow x = 1\end{array}\)

Với \(x = 1\) thì \(k = {4.1^3} + 4.1 = 8\).

Vậy phương trình tiếp tuyến cần tìm là: \(y = 8\left( {x - 1} \right) + 3 \Leftrightarrow y = 8x - 5\).

Chọn A

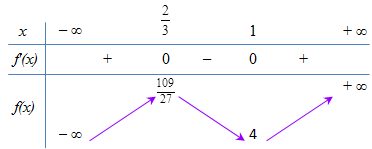
Phương pháp giải:

Lời giải chi tiết:

+ Lập phương trình đường thẳng đi qua\(M(1;2)\)

\( \Rightarrow \)Phương trình đường thẳng có dạng:\(y = k\left( {x - {x_0}} \right) + {y_0}\)

                                         \( \Leftrightarrow y = k\left( {x - 1} \right) + 2 \Leftrightarrow y = kx - k + 2\)

Đường thẳng qua M và tiếp xúc với Đồ thị

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}{x^3} - 2{x^2} + (m - 1)x + 2m = kx - k + 2\\3{x^2} - 4x + (m - 1) = k\end{array} \right.\\ \Leftrightarrow {x^3} - 2{x^2} + mx - x + 2m = 3{x^3} - 4{x^2} + mx - x - 3{x^2} + 4x - m + 1 + 2\\ \Leftrightarrow 2{x^3} - 5{x^2} + 4x + 3 = 3m\,\,(*)\end{array}\)

Để kẻ được 2 tiếp tuyến đến đồ thị \( \Rightarrow \) PT (*) phải có 2 nghiệm

Xét \(f\left( x \right) = 2{x^3} - 5{x^2} + 4x + 3\)

\(f'\left( x \right) = 6{x^2} - 10x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{2}{3}\end{array} \right.\)

BBT:

PT (*) có 2 nghiệm \( \Rightarrow \) Đường thẳng\(y = 3m\) phải cắt đồ thị tại 2 điểm \( \Leftrightarrow \left[ \begin{array}{l}3m = \dfrac{{109}}{{27}}\\3m = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{{109}}{{81}}\\m = \dfrac{4}{3}\end{array} \right..\)

Chọn A

Phương pháp giải:

+ Gọi điểm trên trục tung là \(M\left( {0;m} \right)\)

+ Lập phương trình đường thẳng đi qua\(M\left( {0;m} \right)\)

\( \Rightarrow \) Phương trình đường thẳng có dạng:\(y = k\left( {x - {x_0}} \right) + {y_0} \Leftrightarrow y = k.\left( {x - 0} \right) + m \Leftrightarrow y = kx + m\)

Đường thẳng tiếp tuyến qua \(M\) và tiếp xúc với đồ thị \( \Rightarrow \left\{ \begin{array}{l}kx + m = {x^4} - {x^2} + 1\,\,\,\,\left( 1 \right)\\k = 4{x^3} - 2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Thế (2) vào (1) ta được:

\(\begin{array}{l} \Leftrightarrow m =  - \left( {4{x^3} - 2x} \right)x + {x^4} - {x^2} + 1\\ \Leftrightarrow m =  - 4{x^4} + 2{x^2} + {x^4} - {x^2} + 1\\ \Leftrightarrow m =  - 3{x^4} + {x^2} + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(  *  \right)\end{array}\)

+ Để kẻ được 3 tiếp tuyến tới đồ thị thì PT (*) phải có 3 nghiệm.

Xét \(f\left( x \right) =  - 3{x_{}}^4 + {x_{}}^2 + 1\)

\(f'\left( x \right) =  - 12{x_{}}^3 + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{\sqrt 6 }}{6}\\x =  - \dfrac{{\sqrt 6 }}{6}\\x = 0\end{array} \right.\)

BBT:

Để PT (*) có 3 nghiệm  \( \Rightarrow \) Đường thẳng\(y = m\) phải cắt đồ thị tại 3 điểm \( \Leftrightarrow m = 1.\)

Vậy điểm cần tìm là \(M\left( {0;1} \right).\)

Chọn A

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Gọi phương trình đường thẳng qua \(A\left( {0;\,a} \right)\) có dạng: \(y = k\left( {x - } \right) + a \Leftrightarrow y = kx + a\)

Đường thẳng qua A tiếp xúc với đồ thị \( \Rightarrow \left\{ \begin{array}{l}\dfrac{{x + 2}}{{x - 1}} = kx + a\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\dfrac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}} = k\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Thế \((2)\) vào \((1)\) ta có: \(\dfrac{{x + 2}}{{x - 1}} = \dfrac{{ - 3x}}{{{{\left( {x - 1} \right)}^2}}} + a\)

\(\begin{array}{l} \Leftrightarrow {x^2} + x - 2 =  - 3x + a{x^2} - 2ax + a\\ \Leftrightarrow \left( {1 - a} \right){x^2} + 2\left( {2 + a} \right)x - 2 - a = 0\,\,\,\,\,\left( * \right)\end{array}\)

+ Để kẻ được 2 tiếp tuyến đến đồ thị có 2 tiếp điểm nằm 2 phía trục hoành.

\( \Rightarrow \) Phương trình (*) phải có 2 nghiệm phân biệt \({x_1},{x_2}\) có tung độ trái dấu.

\( \Rightarrow \)\(\left\{ \begin{array}{l}\Delta  > 0\\{y_1}.{y_2} < 0\\a - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\Delta  > 0\\\dfrac{{{x_1} + 2}}{{{x_1} - 1}}.\dfrac{{{x_2} + 2}}{{{x_2} - 1}} < 0\\a \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\Delta  > 0\,\,(1)\\\dfrac{{{x_1}.{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}.{x_2} - \left( {{x_1} + {x_2}} \right) + 1}} < 0\,\,\,(2)\\a \ne 1\end{array} \right.\)

\((1) \Leftrightarrow \Delta  = 4{\left( {2 + a} \right)^2} - 4\left( {1 - a} \right).\left( { - 2 - a} \right) > 0 \Leftrightarrow 12a + 24 > 0 \Leftrightarrow a >  - 2\)

+ Theo Vi-et \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{2\left( {2 + a} \right)}}{{a - 1}}\\{x_1}.{x_2} = \dfrac{{2 + a}}{{a - 1}}\end{array} \right.\)

\(\left( 2 \right) \Leftrightarrow \dfrac{{\dfrac{{2 + a}}{{a - 1}} + \dfrac{{4\left( {2 + a} \right)}}{{a - 1}} + 4}}{{\dfrac{{2 + a}}{{a - 1}} - \dfrac{{2\left( {2 + a} \right)}}{{a - 1}} + 1}} < 0 \Leftrightarrow \left[ \begin{array}{l}\dfrac{{ - 2}}{3} < a < 1\\a > 1\end{array} \right.\)

Kết hợp (1) và (2) \( \Rightarrow a \in \left( {\dfrac{{ - 2}}{3};1} \right) \cup \left( {1; + \infty } \right)\)

Mà \(a \in \left[ { - 2018;\,2018} \right]\) \( \Rightarrow a \in \left( {\dfrac{{ - 2}}{3};1} \right) \cup \left( {1;2018} \right]\) \( \Rightarrow \)Có 2018 giá trị a nguyên.

Chọn C

Phương pháp giải:

Lời giải chi tiết:

\(y = {x^3} - 3{x^2} - 1 \Rightarrow y' = 3{x^2} - 6x\)

Để hệ số góc \({k_{\min }} \Rightarrow y{'_{\min }}\)

\(\begin{array}{l}y'' = 6x - 6 = 0 \Leftrightarrow x = 1\\ \Leftrightarrow y{'_{\min }} = y'\left( 1 \right) =  - 3 \Rightarrow k =  - 3\end{array}\)

Tiếp tuyến tại M của đồ thị có hệ số góc \(k\) bé nhất

\( \Leftrightarrow 3{x^2} - 6x =  - 3 \Leftrightarrow x = 1 \Rightarrow y =  - 3 \Rightarrow M\left( {1; - 3} \right)\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Để \(d:y = 4x + m\)tiếp xúc với \(y = {x^3} + x + 2\)

\( \Leftrightarrow \left\{ \begin{array}{l}4x + m = {x^3} + x + 2\\4 = 3{x^2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^3} - 3x + 2 - m = 0\\\left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.\end{array} \right.\)

Với \(x = 1 \Rightarrow 1 - 3 + 2 - m = 0 \Leftrightarrow m = 0\)

Với \(x =  - 1 \Rightarrow  - 1 + 3 + 2 - m = 0 \Leftrightarrow m = 4\)

Chọn A

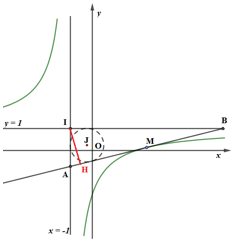
Phương pháp giải:

Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}},\left( {ad - bc,c \ne 0} \right)\)có TCĐ: \(x =  - \dfrac{d}{c}\), TCN: \(y = \dfrac{a}{c}\)và có tâm đối xứng là\(I\left( { - \dfrac{d}{c};\dfrac{a}{c}} \right)\).

Lời giải chi tiết:

Đồ thị hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) có TCĐ \(x =  - 1\), TCN: \(y = 1\) và có tâm đối xứng là \(I\left( { - 1;1} \right)\).

Gọi \(M\left( {{x_0};{y_0}} \right)\)là tiếp điểm;

       A, B lần lượt là giao điểm của tiếp tuyến \(\Delta \) với TCĐ, TCN;

       J, r lần lượt là tâm và bán kính của đường tròn nội tiếp tam giác IAB.

Phương trình tiếp tuyến \(\Delta \): \(y = y'\left( {{x_0}} \right).\left( {x - {x_0}} \right) + {y_0} \Leftrightarrow y = \dfrac{3}{{{{\left( {{x_0} + 1} \right)}^2}}}.\left( {x - {x_0}} \right) + \dfrac{{{x_0} - 2}}{{{x_0} + 1}}\)

Cho \(x =  - 1 \Rightarrow y = \dfrac{3}{{{{\left( {{x_0} + 1} \right)}^2}}}.\left( { - 1 - {x_0}} \right) + \dfrac{{{x_0} - 2}}{{{x_0} + 1}} = \dfrac{{{x_0} - 5}}{{{x_0} + 1}} \Rightarrow A\left( { - 1;\dfrac{{{x_0} - 5}}{{{x_0} + 1}}} \right) \Rightarrow IA = \left| {\dfrac{6}{{{x_0} + 1}}} \right|\)

Cho \(y = 1 \Rightarrow 1 = \dfrac{3}{{{{\left( {{x_0} + 1} \right)}^2}}}.\left( {x - {x_0}} \right) + \dfrac{{{x_0} - 2}}{{{x_0} + 1}} \Leftrightarrow x = 2{x_0} + 1 \Rightarrow B\left( {2{x_0} + 1;1} \right) \Rightarrow IB = 2\left| {{x_0} + 1} \right|\)

\( \Rightarrow IA.IB = 12,\,\,\forall {x_0} \ne  - 1\)

\({S_{IAB}} = \dfrac{1}{2}IA.IB = \dfrac{1}{2}\left( {IA + IB + AB} \right).r\)

\( \Rightarrow r = \dfrac{{IA.IB}}{{IA + IB + AB}} = \dfrac{{IA.IB}}{{IA + IB + \sqrt {I{A^2} + I{B^2}} }}\)

\( = \dfrac{{12}}{{IA + IB + \sqrt {{{\left( {IA + IB} \right)}^2} - 24} }}\)

Ta có: \(IA + IB \ge 2\sqrt {IA.IB}  = 4\sqrt 3 \), dấu “=” xảy ra khi và chỉ khi \(IA = IB\)

Đặt \(IA + IB = t,\,\,t \ge 4\sqrt 3 \), ta có:

\(f\left( t \right) = t + \sqrt {{t^2} - 24}  \Rightarrow f'\left( t \right) = 1 + \dfrac{t}{{\sqrt {{t^2} - 24} }} > 0,\,\,\forall t > 4\sqrt 3 \)

 \( \Rightarrow \) Hàm số đồng biến trên \(\left( {4\sqrt 3 ; + \infty } \right)\)

Ta có: \(f\left( {4\sqrt 3 } \right) = 8\sqrt 3 \)

\( \Rightarrow f\left( t \right) \ge 8\sqrt 3 ,\,\,\forall t \ge 4\sqrt 3  \Rightarrow \dfrac{{12}}{{f\left( t \right)}} \le \dfrac{{12}}{{8\sqrt 3 }} = \dfrac{{\sqrt 3 }}{2},\,\,\forall t \ge 4\sqrt 3 \)

\( \Rightarrow {r_{\max }} = \dfrac{{\sqrt 3 }}{2}\) khi và chỉ khi \(IA = IB = 2\sqrt 3 \) \( \Rightarrow \Delta IAB\) vuông cân tại I có \(d\left( {I;\Delta } \right) = IH = \dfrac{{IA}}{{\sqrt 2 }} = \dfrac{{2\sqrt 3 }}{{\sqrt 2 }} = \sqrt 6 \)

Chọn: C