Phương pháp giải:

- Diện tích tam giác đều cạnh \(a\) là \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\).

- Quay tam giác đều \(ABC\) quanh đường cao \(AH\) ta thu được hình nón có đường sinh \(l = AB = a\), bán kính đáy \(r = \dfrac{{BC}}{2}\).

- Diện tích xung quanh của hình nón có đường sinh \(l\), bán kính đáy \(r\) là: \(\pi rl\).

Lời giải chi tiết:

Giả sử tam giác ABC đều cạnh a  \( \Rightarrow {s_1} = {S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Quay tam giác ABC quanh đường thẳng \(AH\) ta thu được hình nón có đường sinh \(l = AB = a\), bán kính đáy \(r = \dfrac{{BC}}{2} = \dfrac{a}{2}\), do đó diện tích xung quanh của hình nón bằng:  \({s_2} = \pi rl = \pi .\dfrac{a}{2}.a = \dfrac{{\pi {a^2}}}{2}\).

Vậy \(\dfrac{{{s_1}}}{{{s_2}}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{4}}}{{\dfrac{{\pi {a^2}}}{2}}} = \dfrac{{\sqrt 3 }}{{2\pi }}\).

Chọn B.

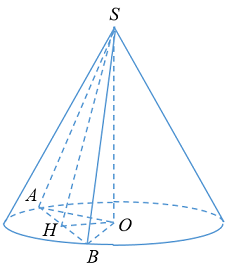
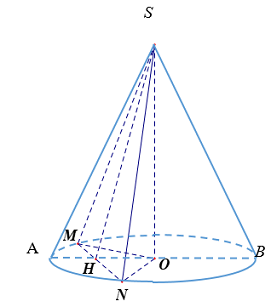
Phương pháp giải:

- Giả sử thiết diện của hình chóp cắt bởi mặt phẳng đi qua đỉnh và cách tâm một khoảng \(\dfrac{a}{3}\) là tam giác \(SAB\). Gọi \(O\) là tâm đáy của hình nón.

- Xác định khoảng cách từ \(O\) đến \(\left( {SAB} \right)\).

- Sử dụng hệ thức lượng và định lí Pytago trong tam giác vuông tính bán kính đáy của hình nón.

- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

Lời giải chi tiết:

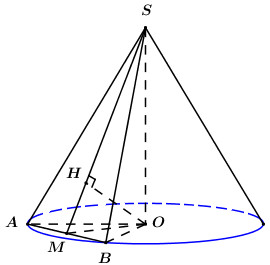
Giả sử thiết diện của hình chóp cắt bởi mặt phẳng đi qua đỉnh và cách tâm một khoảng \(\dfrac{a}{3}\) là tam giác \(SAB\), ta có \(\Delta SAB\) vuông cân tại \(S\).

Gọi \(O\) là tâm đáy của hình nón, gọi \(M\) là trung điểm của \(AB\). Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\,\,\left( {H \in SM} \right)\).

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow SB \bot \left( {SOM} \right) \Rightarrow AB \bot OH\\\left\{ \begin{array}{l}OH \bot AB\\OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SAB} \right)\\ \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH = \dfrac{a}{3}\end{array}\)

Áp dụng hệ thức lượng trong tam giác vuông \(SOM\) ta có:

\(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}}\\ \Leftrightarrow \dfrac{9}{{{a^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{O{M^2}}}\\ \Leftrightarrow \dfrac{1}{{O{M^2}}} = \dfrac{8}{{{a^2}}}\\ \Leftrightarrow OM = \dfrac{{a\sqrt 2 }}{4}\end{array}\)

Lại có \(SM = \dfrac{{SO.OM}}{{OH}} = \dfrac{{a.\dfrac{{a\sqrt 2 }}{4}}}{{\dfrac{a}{3}}} = \dfrac{{3\sqrt 2 a}}{4}\), tam giác \(SAB\) vuông cân tại \(S\) nên \(SM = \dfrac{1}{2}AB\).

\( \Rightarrow AB = 2SM = \dfrac{{3\sqrt 2 a}}{2}\) \( \Rightarrow AM = \dfrac{1}{2}AB = \dfrac{{3\sqrt 2 a}}{4}\).

Áp dụng định lí Pytago trong tam giác vuông \(OAM\) ta có:

\(OA = \sqrt {O{M^2} + A{M^2}}  = \sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{4}} \right)}^2} + {{\left( {\dfrac{{3\sqrt 2 a}}{4}} \right)}^2}}  = \dfrac{{a\sqrt 5 }}{2}\).

Vậy thể tích khối nón là: \(V = \dfrac{1}{3}\pi O{A^2}.SO = \dfrac{1}{3}\pi .{\left( {\dfrac{{a\sqrt 5 }}{2}} \right)^2}.a = \dfrac{{5\pi {a^3}}}{{12}}\).

Chọn A.

Phương pháp giải:

Giả sử mặt phẳng qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông \(SAB\).

- Gọi \(M\) là trung điểm của \(AB\), trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\,\,\left( {H \in SM} \right)\), chứng minh \(OH \bot \left( {SAB} \right)\).

- Xác định góc giữa \(SO\) và \(\left( {SAB} \right)\) là góc giữa \(SO\) và hình chiếu của \(SO\) lên \(\left( {SAB} \right)\).

- Dựa vào diện tích tam giác \(SAB\), tính độ dài các cạnh của tam giác \(ABC\).

- Sử dụng tỉ số lượng giác của góc nhọn và định lí Pytago trong tam giác vuông tính \(SO,\,\,OA\).

- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(R\) là \(V = \dfrac{1}{3}\pi {R^2}h\).

Lời giải chi tiết:

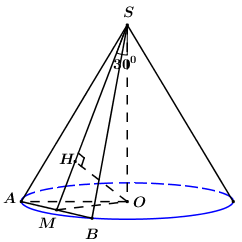
Giả sử mặt phẳng qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông \(SAB\).

Gọi \(M\) là trung điểm của \(AB\) \( \Rightarrow OM \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).

Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\,\,\left( {H \in SM} \right)\) ta có: \(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OH\).

\(\left\{ \begin{array}{l}OH \bot AB\\OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SAB} \right)\) \( \Rightarrow SH\) là hình chiếu của \(SO\) lên \(\left( {SAB} \right)\).

\( \Rightarrow \angle \left( {SO;\left( {SAB} \right)} \right) = \angle \left( {SO;SH} \right) = \angle HSO = \angle MSO = {30^0}\).

Theo bài ra ta có \({S_{\Delta SAB}} = 4\) \( \Leftrightarrow \dfrac{1}{2}SA.SB = 4 \Leftrightarrow S{A^2} = 8 \Leftrightarrow SA = 2\sqrt 2 \).

Tam giác \(SAB\) vuông cân tại \(S\) \( \Rightarrow AB = SA\sqrt 2  = 2\sqrt 2 .\sqrt 2  = 4\) \( \Rightarrow SM = \dfrac{1}{2}AB = 2\).

Xét tam giác vuông \(SOM\)có: \(\left\{ \begin{array}{l}SO = SM.\cos {30^0} = 2.\dfrac{{\sqrt 3 }}{2} = \sqrt 3  = h\\OM = SM.\sin {30^0} = 2.\dfrac{1}{2} = 1\end{array} \right.\).

Áp dụng định lí Pytago trong tam giác vuông \(OAM\) có:

\(OA = \sqrt {O{M^2} + A{M^2}}  = \sqrt {{1^2} + {2^2}}  = \sqrt 5  = R\).

Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {\left( {\sqrt 5 } \right)^2}.\sqrt 3  = \dfrac{{5\sqrt 3 \pi }}{3}\).

Chọn D.

Phương pháp giải:

Diện tích của đường tròn bán kính \(r\) là: \(S = \pi {r^2}.\)

Thể tích khối nón có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \dfrac{1}{3}\pi {R^2}h.\)

Lời giải chi tiết:

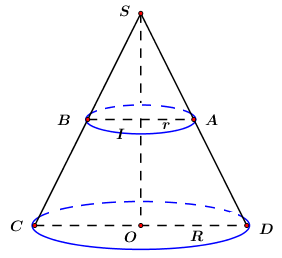
Mặt phẳng vuông góc và đi qua trung điểm \(I\)  của trục \(SO\) của  khối nón cắt khối nón tròn xoay theo giao tuyến là đường tròn tâm \(I\) bán kính \(r.\)

\( \Rightarrow \pi {r^2} = 9\pi  \Leftrightarrow r = 3.\)

Theo định lý Ta-let ta có: \(\dfrac{{SI}}{{SO}} = \dfrac{r}{R} = \dfrac{1}{2}\) \( \Leftrightarrow R = 2r = 6.\)

\( \Rightarrow \) Thể tích khối nón đã cho là: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.6^2}.6 = 72\pi .\)

Chọn C.

Phương pháp giải:

- Tính bán kính ngoại tiếp đáy hình chóp chính là bán kính đáy hình nón.

- Xác định góc giữa mặt bên và mặt đáy là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Tính chiều cao hình chóp chính là chiều cao hình nón. Sử dụng định lí Pytago trong tam giác vuông.

- Áp dụng công thức tính diện tích xung quanh khối nón có đường sinh \(l\), bán kính đáy \(R\) là \({S_{xq}} = \pi Rl\).

Lời giải chi tiết:

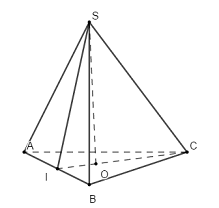
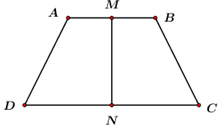
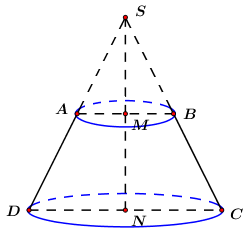
Gọi O là tâm tam giác đều  ABC\( \Rightarrow SO \bot \left( {ABCD} \right)\)

Tam giác ABC đều cạnh a  nên \(CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow OC = \dfrac{2}{3}CI = \dfrac{{a\sqrt 3 }}{3}\) và \(OI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 3 }}{6}\).

\( \Rightarrow \) Bán kính khối nón đỉnh \(S\) có đáy là hình tròn ngoại tiếp tam giác \(ABC\) là \(R = \dfrac{{a\sqrt 3 }}{3}\).

Gọi I là trung điểm của AB ta có: \(\left\{ \begin{array}{l}AB \bot OI\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow AB \bot SI\).

\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\SI \subset \left( {SAB} \right);\,\,SI \bot AB\\CI \subset \left( {ABC} \right);\,\,CI \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABC} \right)} \right) = \angle \left( {SI;CI} \right) = \angle SIC = {60^0}\).

Xét tam giác vuông \(SOI\) có: \(SI = \dfrac{{OI}}{{\cos {{60}^0}}} = \dfrac{{a\sqrt 3 }}{3}\).

Áp dụng định lí Pytago trong tam giác vuông \(SAI\) có: \(SA = \sqrt {S{I^2} + A{I^2}}  = \sqrt {\dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt {21} }}{6}\).

\( \Rightarrow \) Độ dài đường sinh của khối nón đỉnh \(S\) có đáy là hình tròn ngoại tiếp tam giác \(ABC\) là \(l = \dfrac{{a\sqrt {21} }}{6}\).

Vậy diện tích xung quanh của hình nón cần tìm là: \({S_{xq}} = \pi Rl = \pi .\dfrac{{a\sqrt 3 }}{3}.\dfrac{{a\sqrt {21} }}{6} = \dfrac{{\pi {a^2}\sqrt 7 }}{6}\).

Chọn B.

Phương pháp giải:

Diện tích xung quanh hình nón có đường sinh \(l\) và bán kính đáy \(r\) là: \({S_{xq}} = \pi rl.\)

Kéo dài AD và BC cắt nhau tại S.

Quay tam giác SCD quanh trục SN được hình nón (N) đỉnh S, đáy là đường tròn đường kính CD.

Gọi hình nón đỉnh S, đáy là đường tròn đường kính AB là (M).

Khi đó: Diện tích xung quanh hình nón cụt được tạo thành = Diện tích xung quanh hình nón (N) – Diện tích xung quanh hình nón (M).

Lời giải chi tiết:

Kéo dài AD và BC cắt nhau tại S.

Quay tam giác SCD quanh trục SN được hình nón (N) đỉnh S, đáy là đường tròn đường kính CD.

Gọi hình nón đỉnh S, đáy là đường tròn đường kính AB là (M).

Theo định lý Talet ta có: \(\dfrac{{SA}}{{SD}} = \dfrac{{SM}}{{SN}} = \dfrac{{AB}}{{AD}} = \dfrac{{3a}}{{6a}} = \dfrac{1}{2}\)

\( \Rightarrow \dfrac{{SM}}{{SN}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{SM}}{{SM + 2a}} = \dfrac{1}{2}\) \( \Leftrightarrow 2SM = SM + 2a\)\( \Leftrightarrow SM = 2a\)

\( \Rightarrow SN = SM + MN = 4a.\)

Áp dụng định lý Pitago cho các tam giác \(SAM,\,\,SDN\) vuông tại \(M,\,\,N\) ta có:

\(\left\{ \begin{array}{l}S{A^2} = S{M^2} + A{M^2}\\S{D^2} = S{N^2} + D{N^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}S{A^2} = 4{a^2} + {\left( {\dfrac{{3a}}{2}} \right)^2} = \dfrac{{25{a^2}}}{4}\\S{D^2} = {\left( {4a} \right)^2} + {\left( {\dfrac{{6a}}{2}} \right)^2} = 25{a^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}SA = \dfrac{{5a}}{2}\\SD = 5a\end{array} \right..\)

\( \Rightarrow \) Diện tích xung quanh hình chóp cụt cần tính là:

\(\begin{array}{l}{S_{xq\,\,\left( N \right)}} - {S_{xq\,\,\left( M \right)}} = \pi .DN.SD - \pi .SA.AM\\ = \pi .5a.3a - \pi .\dfrac{{5a}}{2}.\dfrac{{3a}}{2} = \dfrac{{45\pi {a^2}}}{4} = 11,25\pi {a^2}.\end{array}\)

Chọn B.

Phương pháp giải:

- Gọi R, h, l lần lượt là bán kính đáy, chiều cao và độ dài đường sinh của cái phễu. Tính h và l theo R.

- Tính diện tích xung quanh của cái phễu: \({S_{xq}} = \pi Rl\).

- Sử dụng BĐT Cô-si: \(a + b + c \ge 3\sqrt[3]{{abc}}\,\,\left( {a,\,\,b,\,\,c \ge 0} \right)\) để tìm GTNN của diện tích xung quanh.

Lời giải chi tiết:

Gọi R, h, l lần lượt là bán kính đáy, chiều cao và độ dài đường sinh của cái phễu.

Khi đó \(V = \dfrac{1}{3}\pi {R^2}h = 2 \Leftrightarrow h = \dfrac{6}{{\pi {R^2}}}\) và \(l = \sqrt {{h^2} + {R^2}}  = \sqrt {\dfrac{{36}}{{{\pi ^2}{R^4}}} + {R^2}} \).

Diện tích xung quanh của hình nón là \({S_{xq}} = \pi Rl = \pi R.\sqrt {\dfrac{{36}}{{{\pi ^2}{R^4}}} + {R^2}}  = \sqrt {\dfrac{{36}}{{{R^2}}} + {\pi ^2}{R^4}} \).

Ta có: \(\dfrac{{36}}{{{R^2}}} + {\pi ^2}{R^4} = \dfrac{{18}}{{{R^2}}} + \dfrac{{18}}{{{R^2}}} + {\pi ^2}{R^4} \ge 3\sqrt[3]{{\dfrac{{18}}{{{R^2}}}.\dfrac{{18}}{{{R^2}}}.{\pi ^2}{R^4}}} = 3\sqrt[3]{{{{\left( {18\pi } \right)}^2}}}\)  (BĐT Cô-si).

Dấu “=” xảy ra \( \Leftrightarrow \dfrac{{18}}{{{R^2}}} = {\pi ^2}{R^4} \Leftrightarrow R = \sqrt[6]{{\dfrac{{18}}{{{\pi ^2}}}}}\).

Vậy \(\min {S_{xq}} = \sqrt {3{{\sqrt[3]{{\left( {18\pi } \right)}}}^2}}  \approx 6,65\,\,\left( {d{m^2}} \right).\)  

Chọn C.

Phương pháp giải:

- Gọi R là bán kính đáy của hình nón. Sử dụng định lí Pytago tính cạnh của thiết diện.

- Tính diện tích của thiết diện và diện tích đáy của hình nón theo R.

- Thay vào giả thiết \(S = \dfrac{{5\sqrt 3 }}{{4\pi }}{S_d}\) tìm R.

- Diện tích toàn phần của hình nón có kính đáy R và đường sinh \(l\) là: \({S_{tp}} = \pi {R^2} + \pi Rl\).

Lời giải chi tiết:

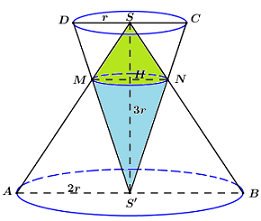
Gọi R là bán kính đáy của hình nón.

Cạnh của thiết diện là: \(SA = \sqrt {S{O^2} + {R^2}}  = \sqrt {1 + {R^2}} \).

Diện tích thiết diện là: \(S = \dfrac{{S{A^2}\sqrt 3 }}{4} = \dfrac{{\left( {1 + {R^2}} \right).\sqrt 3 }}{4}\).

Diện tích đáy của hình nón là \({S_d} = \pi {R^2}\).

Ta có: \(S = \dfrac{{5\sqrt 3 }}{{4\pi }}{S_d} \Leftrightarrow \dfrac{{\left( {1 + {R^2}} \right)\sqrt 3 }}{4} = \dfrac{{\pi {R^2}.5\sqrt 3 }}{{4\pi }}\) \( \Leftrightarrow R = \dfrac{1}{2} \Rightarrow SA = \dfrac{{\sqrt 5 }}{2} = l\).

Vậy diện tích toàn phần của hình nón là: \({S_{tp}} = \pi {R^2} + \pi Rl = \pi .\dfrac{1}{4} + \pi .\dfrac{1}{2}.\dfrac{{\sqrt 5 }}{2} = \dfrac{{\left( {\sqrt 5  + 1} \right)\pi }}{4}.\)

Chọn C.

Phương pháp giải:

- Xác định thể tích phần chung là thể tích của hai khối nón.

- Sử dụng định lí Ta-lét để tính chiều cao và bán kính đáy của từng khối nón.

- Sử dụng công thức tính thể tích khối nón: Thể tích khối nón có chiều cao h, bán kính đáy r là \(V = \dfrac{1}{3}\pi {r^2}h\).

Lời giải chi tiết:

Giả giử một mặt phẳng chứa trục SS’ cắt hình nón đỉnh S theo một thiết diện qua trục là \(\Delta SAB\), cắt hình nón S’ theo một thiết diện qua trục là \(\Delta S'CD\).

Gọi \(M = SA \cap S'D,\,\,N = SB \cap S'C\), \(H = SS' \cap MN\).

Dễ thấy \(AB\parallel CD\) (cùng vuông góc với SS’), do đó áp dụng định lí Ta-lét ta có:

\(\dfrac{{SM}}{{AM}} = \dfrac{{SD}}{{S'A}} = \dfrac{r}{{2r}} = \dfrac{1}{2}\), \(\dfrac{{SN}}{{BN}} = \dfrac{{SC}}{{S'B}} = \dfrac{r}{{2r}} = \dfrac{1}{2}\).

\( \Rightarrow \dfrac{{SM}}{{AM}} = \dfrac{{SN}}{{BN}} \Rightarrow MN\parallel AB\parallel CD\) (Định lí Ta-lét đảo).

\(\begin{array}{l} \Rightarrow \dfrac{{SH}}{{SS'}} = \dfrac{{MH}}{{S'A}} = \dfrac{{SM}}{{SA}} = \dfrac{1}{3}\\ \Rightarrow \left\{ \begin{array}{l}SH = \dfrac{1}{3}SS' = \dfrac{1}{3}.3r = r\\MH = \dfrac{1}{3}S'A = \dfrac{1}{3}.2r = \dfrac{{2r}}{3}\end{array} \right.\end{array}\)

\( \Rightarrow HS' = SS' - SH = 3r - r = 2r\).

Thể tích phần chung của hai khối nón bao gồm:

+ \({V_1}\) là thể tích khối nón đỉnh S có chiều cao \({h_1} = SH = r\), bán kính \({R_1} = MH = \dfrac{{2r}}{3}\)

\( \Rightarrow {V_1} = \dfrac{1}{3}\pi R_1^2{h_1} = \dfrac{1}{3}\pi .{\left( {\dfrac{{2r}}{3}} \right)^2}.r = \dfrac{{4\pi {r^3}}}{{27}}\).

+ \({V_2}\) là thể tích khối nón đỉnh \({S_1}\) có chiều cao \({h_2} = S'H = 2r\), bán kính \({R_2} = MH = \dfrac{{2r}}{3}\)

\( \Rightarrow {V_2} = \dfrac{1}{3}\pi R_2^2{h_2} = \dfrac{1}{3}\pi .{\left( {\dfrac{{2r}}{3}} \right)^2}.2r = \dfrac{{8\pi {r^3}}}{{27}}\).

Vậy thể tích phần chung của hai khối nón là: \(V = {V_1} + {V_2} = \dfrac{{4\pi {r^3}}}{{27}} + \dfrac{{8\pi {r^3}}}{{27}} = \dfrac{{4\pi {r^3}}}{9}\).

Chọn C.

Phương pháp giải:

- Gọi M là trung điểm của CD, I là giao điểm của AD và BC. Chứng minh \(\Delta ICD\) vuông tại I.

- Gọi \({V_1}\) là thể tích khối tròn xoay khi xoay tam giác vuông ICD quanh cạnh AD, \({V_2}\) là thể tích khối tròn xoay khi xoay tam giác vuông IAB quanh cạnh AD. Tính \({V_1},\,\,{V_2}\).

- Sử dụng công thức tính thể tích khối nón có chiều cao h, bán kính đáy r là \(V = \dfrac{1}{3}\pi {r^2}h\).

- Thể tích khối tròn xoay khi xoay hình thang ABCD quanh cạnh AD là: \(V = {V_1} - {V_2}\).

Lời giải chi tiết:

Gọi M là trung điểm của CD và I là giao điểm của AD và BC.

Khi đó ta có MC = MD = 5 = AB, lại có AB // MD, AB // MC

=> ABMD và ABCM là các hình bình hành.

=> AM = BC = 3 và BM = AD = 4.

Xét tam giác ADM có: \(\left\{ \begin{array}{l}A{D^2} + A{M^2} = {4^2} + {3^2} = 25\\M{D^2} = {5^2} = 25\end{array} \right.\) \( \Rightarrow \Delta ADM\) vuông tại A (định lí Pytago đảo).

CMTT: \(\Delta BCM\) vuông tại B.

\( \Rightarrow AM \bot AD \Rightarrow BC \bot AD\) hay \(IC \bot ID \Rightarrow \Delta ICD\) vuông tại I.

Lại có AB // CD, \(AB = \dfrac{1}{2}CD\) nên AB là đường trung bình của tam giác ICD, suy ra A và B lần lượt là trung điểm của ID và IC.

Gọi \({V_1}\) là thể tích khối tròn xoay khi xoay tam giác vuông ICD quanh cạnh AD.

\( \Rightarrow {V_1}\) là khối nón có chiều cao \({h_1} = ID = 2AD = 8\), \({r_1} = IC = 2BC = 6\).

\( \Rightarrow {V_1} = \dfrac{1}{3}\pi r_1^2{h_1} = \dfrac{1}{3}\pi {.6^2}.8 = 96\pi \).

 Gọi \({V_2}\) là thể tích khối tròn xoay khi xoay tam giác vuông IAB quanh cạnh AD.

\( \Rightarrow {V_2}\) là khối nón có chiều cao \({h_2} = AI = AD = 4\), \({r_2} = IB = BC = 3\).

\( \Rightarrow {V_1} = \dfrac{1}{3}\pi r_2^2{h_2} = \dfrac{1}{3}\pi {.3^2}.4 = 12\pi \).

Vậy thể tích khối tròn xoay khi xoay hình thang ABCD quanh cạnh AD là: \(V = {V_1} - {V_2} = 96\pi  - 12\pi  = 84\pi \).

Chọn B.

Phương pháp giải:

- Xác định khoảng cách từ O đến \(\left( P \right)\).

- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính chiều cao và đáy của tam giác thiết diện.

Lời giải chi tiết:

Giả sử \(\left( P \right)\) cắt hình nón theo thiết diện là \(\Delta SAB\) cân tại \(S\).

Gọi \(O\) là tâm mặt đáy, \(M\) là trung điểm của \(AB\) ta có:

\(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right)\).

Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\) ta có \(\left\{ \begin{array}{l}OH \bot SM\\OH \bot AB\end{array} \right. \Rightarrow OH \bot \left( {SAB} \right)\) hay \(OH \bot \left( P \right)\) \( \Rightarrow d\left( {O;\left( P \right)} \right) = OH = a\).

Áp dụng hệ thức lượng trong tam giác vuông SOM có:

\(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}}\\ \Leftrightarrow \dfrac{1}{{{a^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{1}{{O{M^2}}}\\ \Rightarrow \dfrac{1}{{O{M^2}}} = \dfrac{1}{{2{a^2}}} \Rightarrow OM = a\sqrt 2 \end{array}\)

Áp dụng định lí Pytago ta có:

\(\begin{array}{l}AM = \sqrt {O{A^2} - O{M^2}}  = \sqrt {4{a^2} - 2{a^2}}  = a\sqrt 2 \\ \Rightarrow AB = 2AM = 2a\sqrt 2 \\SM = \sqrt {S{O^2} + O{M^2}}  = \sqrt {2{a^2} + 2{a^2}}  = 2a\end{array}\)

Vậy

\({S_{\Delta SAB}} = \dfrac{1}{2}SM.AB = \dfrac{1}{2}.2a.2a\sqrt 2  = 2\sqrt 2 {a^2}\).

Chọn D.

Phương pháp giải:

- Tính chiều cao của hình nón.

- Xác định thiết diện của mặt phẳng đi qua đỉnh của hình nón và tạo với mặt phẳng đáy của hình nón một góc bằng \({60^0}\) và mặt đáy của hình nón. Thiết diện đó là tam giác cân.

- Sử dụng định lí Pytago và tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao và cạnh đáy tương ứng của thiết diện.

- Tính diện tích tam giác : \({S_\Delta } = \dfrac{1}{2}a{h_a}\)

Lời giải chi tiết:

Hình nón có có đường sinh bằng \(a\) và góc ở đỉnh bằng \({90^0}\) \( \Rightarrow \angle OSA = {45^0}\).

\( \Rightarrow \Delta SOA\) vuông cân tại \(O\)\( \Rightarrow h = r = \dfrac{l}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}.\)

Thiết diện là tam giác \(SAB\) cân tại \(S\). Gọi \(I\) là trung điểm của \(AB\) ta có:

   \(SI \bot AB\) (do \(\Delta SAB\) cân tại \(S\)).

   \(OI \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).

Ta có:

\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {OAB} \right) = AB\\\left( {SAB} \right) \supset SI \bot AB\\\left( {OAB} \right) \supset OI \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {OAB} \right)} \right) = \angle \left( {SI;OI} \right) = \angle SIO = {60^0}\).

\( \Rightarrow IO = \dfrac{{SO}}{{\tan {{60}^0}}} = \dfrac{{\dfrac{a}{{\sqrt 2 }}}}{{\sqrt 3 }} = \dfrac{a}{{\sqrt 6 }},\,SI = \dfrac{{SO}}{{\sin {{60}^0}}} = \dfrac{{\dfrac{a}{{\sqrt 2 }}}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{a\sqrt 6 }}{3}.\)

Áp dụng định lí Pytago trong tam giác vuông \(OAI\) ta có:

\(IA = \sqrt {O{A^2} - O{I^2}}  = \sqrt {{{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2} - {{\left( {\dfrac{a}{{\sqrt 6 }}} \right)}^2}}  = \dfrac{a}{{\sqrt 3 }} \Rightarrow AB = \dfrac{{2a}}{{\sqrt 3 }}\)

\( \Rightarrow {S_{SAB}} = \dfrac{1}{2}.SI.AB = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{2a}}{{\sqrt 3 }} = \dfrac{{{a^2}\sqrt 2 }}{3}.\)

Chọn A.

Phương pháp giải:

Công thức tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \dfrac{1}{3}\pi {r^2}h.\)

Lời giải chi tiết:

Gọi hình nón có đỉnh \(S\) như hình vẽ.

Khi đó ta có thiết diện là \(\Delta SAB\) đều.

\(\begin{array}{l} \Rightarrow {S_{SAB}} = 9\sqrt 3  \Leftrightarrow \dfrac{{S{A^2}.\sqrt 3 }}{4} = 9\sqrt 3  \Leftrightarrow SA = 6.\\ \Rightarrow SA = SB = AB = 6\end{array}\)

Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB\) và \(AH = \dfrac{1}{2}AB = 3\).

Áp dụng định lí Pytago trong tam giác vuông \(SOA\) ta có:

\(OA = \sqrt {S{A^2} - S{O^2}}  = \sqrt {{6^2} - {{\left( {2\sqrt 5 } \right)}^2}}  = 4 = r\).

Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {4^2}.2\sqrt 5  = \dfrac{{32\sqrt 5 \pi }}{3}\).

Chọn A.

Phương pháp giải:

- Gọi thiết diện của hình nón cắt bởi \(\left( \alpha  \right)\) là tam giác đều \(SAB\), \(I\) là tâm đáy, \(M\) là trung điểm của \(AB\).

- Xác định góc giữa \(SI\) và \(\left( {SAB} \right)\) là góc giữa \(SI\) và hình chiếu của \(SI\) lên \(\left( {SAB} \right)\).

- Sử dụng tính chất tam giác vuông cân và định lí Pytago tính bán kính đáy hình nón.

- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

Lời giải chi tiết:

Gọi thiết diện của hình nón cắt bởi \(\left( \alpha  \right)\) là tam giác đều \(SAB\), \(I\) là tâm đáy, \(M\) là trung điểm của \(AB\).

Ta có: \(\left\{ \begin{array}{l}AB \bot IM\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SIM} \right)\) \( \Rightarrow AB \bot SM\).

Trong \(\left( {SIM} \right)\) kẻ \(IH \bot SM\,\,\left( {H \in SM} \right)\) ta có:

\(\left\{ \begin{array}{l}IH \bot SM\\IH \bot AB\,\,\left( {AB \bot \left( {SIM} \right)} \right)\end{array} \right.\) \( \Rightarrow IH \bot \left( {SAB} \right)\). Do đó \(SH\) là hình chiếu của \(SI\) lên \(\left( {SAB} \right)\).

\( \Rightarrow \angle \left( {SI;\left( {SAB} \right)} \right) = \angle \left( {SI;SH} \right) = \angle \left( {SI;SM} \right) = \angle ISM = {45^0}\). Suy ra tam giác .. vuông cân tại \(I\).

\( \Rightarrow IM = SI = 3,\,\,SM = 3\sqrt 2 \).

Vì \(SM\) là chiều cao của tam giác đều \(SAB\) \( \Rightarrow SM = \dfrac{{AB\sqrt 3 }}{2}\) \( \Leftrightarrow 3\sqrt 2  = \dfrac{{AB\sqrt 3 }}{2} \Leftrightarrow AB = 2\sqrt 6 \).

\( \Rightarrow MA = MB = \dfrac{1}{2}AB = \sqrt 6 \).

Áp dụng định lí Pytago trong tam giác vuông \(AMI\) có: \(IA = \sqrt {I{M^2} + M{A^2}}  = \sqrt {{3^2} + {{\left( {\sqrt 6 } \right)}^2}}  = \sqrt {15} \).

\( \Rightarrow \) Bán kính đáy hình nón là \(R = IA = \sqrt {15} \).

Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi .I{A^2}.SI = \dfrac{1}{3}\pi .{\left( {\sqrt {15} } \right)^2}.3 = 15\pi \).

Chọn D.

Phương pháp giải:

- Xác định khoảng cách từ tâm mặt đáy hình nón đến \(\left( \alpha  \right)\).

- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính bán kính đáy \(r\) và đường sinh \(l\) của hình nón.

- Diện tích xung quanh của hình nón có kính đáy \(r\) và đường sinh \(l\) là: \({S_{xq}} = \pi rl\).

Lời giải chi tiết:

Gọi thiết diện của hình nón cắt bởi \(\left( \alpha  \right)\) là tam giác đều \(SAB\) và \(I\) là tâm đáy của hình nón.

Gọi \(M\) là trung điểm của \(AB\) ta có \(IM \bot AB\).

Ta có: \(\left\{ \begin{array}{l}AB \bot IM\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SIM} \right)\).

Trong \(\left( {SIM} \right)\) kẻ \(IH \bot SM\,\,\left( {H \in SM} \right)\) ta có: \(\left\{ \begin{array}{l}HI \bot AB\,\,\left( {AB \bot \left( {SIM} \right)} \right)\\IH \bot SM\end{array} \right.\) \( \Rightarrow IH \bot \left( {SAB} \right)\).

\( \Rightarrow d\left( {I;\left( {SAB} \right)} \right) = IH = \dfrac{2}{{\sqrt 3 }}\).

Áp dụng hệ thức lượng trong tam giác vuông \(SIM\) ta có:

\(\dfrac{1}{{M{I^2}}} = \dfrac{1}{{I{H^2}}} - \dfrac{1}{{S{I^2}}} = \dfrac{3}{4} - \dfrac{1}{2} = \dfrac{1}{4} \Rightarrow MI = 2\).

Áp dụng định lí Pytago trong tam giác vuông \(SIM\) ta có: \(SM = \sqrt {S{I^2} + M{I^2}}  = \sqrt {2 + 4}  = \sqrt 6 \).

Vì \(SM\) là đường cao trong tam giác đều \(ABC\) nên \(SM = \dfrac{{AB\sqrt 3 }}{2} \Rightarrow AB = \dfrac{{2SM}}{{\sqrt 3 }} = 2\sqrt 2  = SA = l\).

\( \Rightarrow AM = \dfrac{1}{2}AB = \sqrt 2 \).

Áp dụng định lí Pytago trong tam giác vuông \(AIM\) ta có: \(r = IA = \sqrt {I{M^2} + A{M^2}}  = \sqrt {4 + 2}  = \sqrt 6 \).

Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .\sqrt 6 .2\sqrt 2  = 4\pi \sqrt 3 \).

Chọn D.

Phương pháp giải:

Thể tích khối nón  có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \dfrac{1}{3}\pi {R^2}h.\)

Lời giải chi tiết:

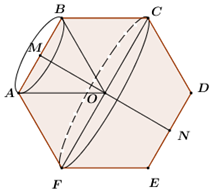
Gọi \(O\) là tâm đường tròn ngoại tiếp \(\Delta BCD.\)

Ta có bán kính đường tròn ngoại tiếp \(\Delta BCD\) là: \(R = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}.\)

Áp dụng định lý Pitago cho \(\Delta ABO\) vuông tại \(O\) ta có:

\(\begin{array}{l}OA = \sqrt {A{B^2} - O{B^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}}  = \dfrac{{a\sqrt 6 }}{3}.\\ \Rightarrow {V_{non}} = \dfrac{1}{3}\pi .O{B^2}.OA = \dfrac{1}{3}\pi .\dfrac{{{a^2}}}{3}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{\pi {a^3}\sqrt 6 }}{{27}}.\end{array}\)

Chọn  A.

Phương pháp giải:

Khối nón cụt có đáy lớn \(R\), đáy nhỏ \(r\), chiều cao \(h\) có thể tích \(V = \frac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\).

Lời giải chi tiết:

Do \(ABCDEF\) là lục giác đều nên \(\Delta OAB\) đều.

Lại có \(OA = OB = a\) nên tam giác \(ABC\) đều cạnh \(a\) \( \Rightarrow AB = a\) và trung tuyến \(OM\) đồng thời là đường cao và \(OM = \frac{{a\sqrt 3 }}{2}\).

Khi xoay hình lục giác đều quanh đường thẳng \(MN\), ta được khối tròn xoay có thể tích bằng 2 lần thể tích hình nón cụt có đáy lớn \(R = OF = a\), đáy nhỏ \(r = AM = \frac{a}{2}\), đường cao \(h = OM = \frac{{a\sqrt 3 }}{2}\).

Vậy thể tích khối tròn xoay cần tính là:

\(V = 2.\frac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\)\( = \frac{{2\pi }}{3}.\frac{{a\sqrt 3 }}{2}\left( {{a^2} + \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2}} \right) = \frac{{7\sqrt 3 \pi {a^3}}}{{12}}\).

Chọn D.

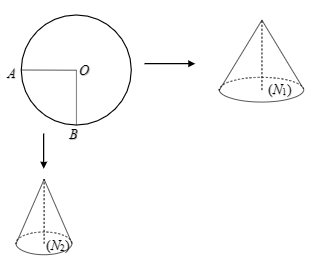
Phương pháp giải:

- Khối nón có bán kính đáy \(r\) và đường sinh \(l\), chiều cao \(h\) có diện tích toàn phần \({S_{tp}} = \pi rl + \pi {r^2}\), thể tích \(V = \frac{1}{3}\pi {r^2}h\).

- Biểu diễn \(l\), \(h\) theo \(r\) và \(a\).

- Áp dụng BĐT Cô-si cho hai số không âm \(a,\,\,b\): \(\sqrt {ab}  \le \frac{{a + b}}{2}\).

Lời giải chi tiết:

Giả sử hình nón có bán kính đáy \(r\) và đường sinh \(l\), khi đó chiều cao của khối nón là \(h = \sqrt {{l^2} - {r^2}} \).

Khi đó diện tích toàn phần của hình nón là \({S_{tp}} = \pi rl + \pi {r^2}\).

Theo bài ra ta có: \({S_{tp}} = \pi rl + \pi {r^2} = \pi {\left( {a\sqrt 2 } \right)^2}\)\( \Leftrightarrow rl + {r^2} = 2{a^2}\)\( \Leftrightarrow l = \frac{{2{a^2} - {r^2}}}{r}\).

Thể tích khối nón là \(V = \frac{1}{3}\pi {r^2}\sqrt {{l^2} - {r^2}} \)\( = \frac{1}{3}\pi {r^2}\sqrt {{{\left( {\frac{{2{a^2} - {r^2}}}{r}} \right)}^2} - {r^2}} \).

\( \Rightarrow V = \frac{1}{3}\pi {r^2}\sqrt {\frac{{4{a^4} - 4{a^2}{r^2} + {r^4} - {r^4}}}{{{r^2}}}} \) \( = \frac{1}{3}\pi {r^2}\frac{{\sqrt {4{a^4} - 4{a^2}{r^2}} }}{r}\)\( = \frac{1}{3}\pi 2ar\sqrt {{a^2} - {r^2}} \).

Áp dụng BĐT Cô-si cho hai số dương \(r\) và \(\sqrt {{a^2} - {r^2}} \) ta có: \(r\sqrt {{a^2} - {r^2}}  \le \frac{{{r^2} + {a^2} - {r^2}}}{2} = \frac{{{a^2}}}{2}\).

\( \Rightarrow V \le \frac{{2\pi }}{3}.a.\frac{{{a^2}}}{2} = \frac{{\pi {a^3}}}{3}\).

Vậy thể tích lớn nhất của khối nón là \(\frac{{\pi {a^3}}}{3}\), đạt được khi \(r = \sqrt {{a^2} - {r^2}} \)\( \Leftrightarrow r = \frac{{a\sqrt 2 }}{2}\).

Chọn B.

Phương pháp giải:

- Áp dụng công thức tính diện tích hình tròn để tìm độ dài cung nhỏ và cung lớn \(AB\).

- Độ dài cung nhỏ, cung lớn \(AB\) lần lượt là chu vi đáy của hai hình nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\).

- Tính bán kính đáy của hai hình nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\).

- Tính chiều cao của hai hình nón \(\left( {{N_1}} \right)\) và \(\left( {{N_2}} \right)\).

- Tính lần lượt thể tích các hình nón. Hình nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

- Tìm tỉ số thể tích hai khối nón.

Lời giải chi tiết:

Chu vi đường tròn \(\left( {O;R} \right)\) là \(C = 2\pi R\).

Gọi \({r_1},\,\,{r_2}\) lần lượt là bán kính đáy của hình nón \(\left( {{N_1}} \right),\,\,\left( {{N_2}} \right)\).

Chu vi đáy hình nón \(\left( {{N_1}} \right)\) là: \({C_1} = \dfrac{3}{4}C = \dfrac{3}{4}.2\pi R = \dfrac{{3\pi R}}{2}\).

\( \Rightarrow 2\pi {r_1} = \dfrac{{3\pi R}}{2} \Rightarrow {r_1} = \dfrac{{3R}}{4}\)  

Tương tự ta tính được \({r_2} = \dfrac{R}{4}\)

Hai hình nón đều có đường sinh \(l = R\)

Nên \({h_1} = \sqrt {{l^2} - r_1^2}  = \dfrac{{\sqrt 7 }}{4}R;\)\({h_2} = \sqrt {{l^2} - r_1^2}  = \dfrac{{\sqrt {15} }}{4}R.\)

\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{1}{3}\pi {r_1}^2{h_1}}}{{\dfrac{1}{3}\pi {r_2}^2{h_2}}} = \dfrac{{{r_1}^2{h_1}}}{{{r_2}^2{h_2}}} = \dfrac{{\dfrac{{9{R^2}}}{{16}}.\dfrac{{\sqrt 7 }}{4}R}}{{\dfrac{{{R^2}}}{{16}}.\dfrac{{\sqrt {15} }}{4}R}} = \dfrac{{3\sqrt {105} }}{5}\)

Chọn A.

Phương pháp giải:

- Chia thể tích khối tròn xoay ra thành những phần nhỏ rồi cộng vào.

- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

- Thể tích khối nón cụt có chiều cao \(h\), hai bán kính đáy \({r_1},\,\,{r_2}\) là: \(V = \dfrac{h}{3}\left( {r_1^2 + {r_1}{r_2} + r_2^2} \right)\).

Lời giải chi tiết:

Lấy điểm \(A',\,\,B'\)  lần lượt là điểm đối xứng với \(A,\,\,B\) qua \(CD\).

Gọi \(H,\,\,C\) là trung điểm của \(BB',\,\,AA'\) .

Ta có các tam giác \(ABC,\,\,HBC\) là các tam giác vuông cân tại \(B,\,\,H\).

\(\begin{array}{l}AC = \sqrt {B{C^2} + A{B^2}}  = a\sqrt 2  = CD\\BH = \dfrac{{BC}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }} = CH\end{array}\)

Gọi \({V_1}\)  là thể tích khối nón chiều cao \(CD\), đường kính đáy \(AA'\).

\( \Rightarrow {V_1} = \dfrac{1}{3}.\pi A{C^2}.CD = \dfrac{1}{3}\pi {\left( {a\sqrt 2 } \right)^2}.a\sqrt 2  = \dfrac{{2\sqrt 2 \pi {a^3}}}{3}\)

Gọi \({V_2}\) là thể tích khối nón cụt có chiều cao \(CH\), đáy nhỏ bán kính \(BH\), đáy lớn bán kính \(AC\).

\(\begin{array}{l} \Rightarrow {V_2} = \dfrac{{\pi .CH}}{3}.\left( {A{C^2} + B{H^2} + AC.BH} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\pi \dfrac{a}{{\sqrt 2 }}}}{3}.\left( {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2} + \dfrac{a}{{\sqrt 2 }}.a\sqrt 2 } \right) = \dfrac{{7\sqrt 2 \pi {a^3}}}{{12}}\end{array}\)

Gọi \({V_3}\)là thể tích khối nón chiều cao \(CH\), bán kính đáy \(BH\).

\( \Rightarrow {V_3} = \dfrac{1}{3}\pi B{H^2}.CH = \dfrac{1}{3}\pi {\left( {\dfrac{a}{{\sqrt 2 }}} \right)^2}.\dfrac{a}{{\sqrt 2 }} = \dfrac{{\sqrt 2 \pi {a^3}}}{{12}}\)

Vậy \(V = {V_1} + {V_2} - {V_3} = \dfrac{{2\sqrt 2 \pi {a^3}}}{3} + \dfrac{{7\sqrt 2 \pi {a^3}}}{{12}} - \dfrac{{\sqrt 2 \pi {a^3}}}{{12}} = \dfrac{{7\sqrt 2 \pi {a^3}}}{6}.\)

Chọn D.

Phương pháp giải:

Khi cắt hình nón bởi một mặt phẳng đi qua đỉnh và cách tâm của đáy một khoảng bằng 2 ta được một tam giác cân.

Tính chiều cao và độ dài đáy của thiết diện để tính diện tích của thiết diện đó.

Lời giải chi tiết:

Gọi \(S\) là đỉnh, \(I\) là tâm đường tròn đáy của hình nón đã cho.

Mặt phẳng đi qua đỉnh của hình nón và cách tâm của đáy một khoảng bằng 2 cắt đường tròn đáy theo dây cung \(AB\)

Gọi \(M\) là trung điểm của \(AB\). Qua \(I\) kẻ \(IH \bot SM\left( {H \in SM} \right)\).

Ta có:

\(IA = IB = 3\) nên tam giác \(IAB\) cân tại \(I\) hay \(IM \bot AB\)     (1)

\(SI \bot \left( {IAB} \right) \Rightarrow SI \bot AB\)      (2)

Từ (1) và (2) suy ra \(AB \bot \left( {SIM} \right) \Rightarrow AB \bot IH\) mà \(IH \bot SM\) nên \(IH \bot \left( {SAB} \right)\)

Khoảng cách từ tâm đến mp \(\left( {SAB} \right)\) bằng 2 nên \(IH = 2\)

Tam giác \(SIM\) vuông tại \(I,\) có đường cao \(IH\) nên:

\(\dfrac{1}{{I{H^2}}} = \dfrac{1}{{S{I^2}}} + \dfrac{1}{{I{M^2}}} \Leftrightarrow \dfrac{1}{{{2^2}}} = \dfrac{1}{{{4^2}}} + \dfrac{1}{{I{M^2}}} \Rightarrow IM = \dfrac{{4\sqrt 3 }}{3}\)

\(S{M^2} = S{I^2} + I{M^2} = {4^2} + {\left( {\dfrac{{4\sqrt 3 }}{3}} \right)^2} \Rightarrow SM = \dfrac{{8\sqrt 3 }}{3}\)

Tam giác \(IAM\) vuông tại \(M\) nên \(AM = \sqrt {I{A^2} - I{M^2}}  = \dfrac{{\sqrt {33} }}{3} \Rightarrow AB = \dfrac{{2\sqrt {33} }}{3}\)

Tam giác \(SAB\) có \(SM \bot AB\) nên diên tích tam giác \(SAB\) là:      

\({S_{\Delta SAB}} = \dfrac{1}{2}SM.AB = \dfrac{1}{2}.\dfrac{{8\sqrt 3 }}{3}.\dfrac{{2\sqrt {33} }}{3} = \dfrac{{8\sqrt {11} }}{3}\)

Vậy diện tích thiết diện bằng \(\dfrac{{8\sqrt {11} }}{3}\) (đvdt)

Chọn D.

Phương pháp giải:

Tính chiều cao \(h\) và bán kính đáy \(r\) của khối nón.

Thể tích của khối nón được tính bằng công thức: \(V = \dfrac{1}{3}\pi h{r^2}\)

Lời giải chi tiết:

Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(O'\) là giao điểm của \(A'C'\) và \(B'D'\).

Khối nón đã cho có đỉnh là \(O\), đường tròn đáy là đường tròn tâm \(O'\) ngoại tiếp hình chữ nhật \(A'B'C'D'\).

Do đó khối nón trên có chiều cao là \(h = OO' = AA' = 3a\) và bán kính đường tròn đáy là

\(r = O'A' = \dfrac{1}{2}A'C' = \dfrac{1}{2}\sqrt {A'B{'^2} + B'C{'^2}} \)  \( = \dfrac{1}{2}\sqrt {{a^2} + {{\left( {2a} \right)}^2}}  = \dfrac{{\sqrt 5 }}{2}a\)

Vậy thể tích của khối nón đã cho là  \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}.\pi .{\left( {\dfrac{{\sqrt 5 }}{2}a} \right)^2}.3a = \dfrac{{5\pi {a^3}}}{4}\)

Chọn B.

Phương pháp giải:

Tìm bán kính đáy và đường sinh của hình nón.

Áp dụng công thức tính diện tích xung quanh của hình nón.

Lời giải chi tiết:

Gọi O là tâm hình vuông ABCD \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO = 2a\)

Kẻ \(OH \bot BC \Rightarrow OH\) là bán kính đáy của hình nón cần tìm.

SH là đường sinh của hình nón đó.

Ta có \(OH = \frac{{BC}}{2} = \frac{a}{2}\) mà \(SO = 2a \Rightarrow SH = \frac{{a\sqrt {17} }}{2}\)

Áp dụng công thức tính diện tích xung quanh hình nón ta có:

\({S_{xq}} = \pi Rl = \pi .OH.SH = \frac{{\pi {a^2}\sqrt {17} }}{4}\)

Chọn C.

Phương pháp giải:

Sử dụng công thức lượng giác tring tam giác.

Áp dụng công thức tính diện tích xung quanh và thể tích.

Lời giải chi tiết:

\(\Delta SAO\) vuông tại O; có \(SA = a\sqrt 2 ;\angle SAO = 60^\circ  \Rightarrow \left\{ \begin{array}{l}R = AO = \cos 60^\circ .SA = \frac{{a\sqrt 2 }}{2}\\h = SO = \sin 60^\circ .SA = \frac{{a\sqrt 6 }}{2}\end{array} \right.\)

Khi đó  \({S_{xq}} = \pi Rl = \pi {a^2}.;\,\,V = \pi Rh = \frac{{\sqrt 6 }}{2}{a^{3.}}\)

Chọn A.

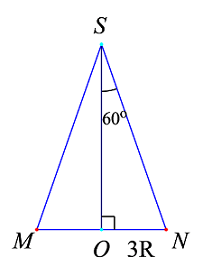
Phương pháp giải:

- Xác định khoảng cách từ tâm đến mặt phẳng thiết diện.

- Áp dụng hệ thức lượng trong tam giác vuông và định lí Pytago để tính cạnh đáy và chiểu cao của thiết diện, từ đó tính diện tích thiết diện.

Lời giải chi tiết:

Gọi thiết diện qua đỉnh là \(\Delta SAB\) ta có \(SA = SB = l\) nên \(\Delta SAB\) cân tại \(S\).

Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot AB\) và \(OH \bot AB\).

\( \Rightarrow AB \bot \left( {SOH} \right)\).

Trong \(\left( {SOH} \right)\) kẻ \(OK \bot SH\,\,\left( {K \in SH} \right)\) ta có

\(\left\{ \begin{array}{l}AB \bot OK\,\,\left( {AB \bot \left( {SOH} \right)} \right)\\OK \bot SH\end{array} \right.\) \( \Rightarrow OK \bot \left( {SAB} \right) \Rightarrow OK = \frac{{3a}}{2}\).

Áp dụng hệ thức lượng trong tam giác vuông \(SOH\) có:

\(\frac{1}{{O{K^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{H^2}}}\) \( \Leftrightarrow \frac{1}{{{{\left( {\frac{{3a}}{2}} \right)}^2}}} = \frac{1}{{{{\left( {2a} \right)}^2}}} + \frac{1}{{O{H^2}}}\)\( \Leftrightarrow OH = \frac{{6a\sqrt 7 }}{7}\).

Áp dụng định lí Pytago trong tam giác vuông \(SOH\) có:

\(SH = \sqrt {S{O^2} + O{H^2}} \)\( = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{{6a\sqrt 7 }}{7}} \right)}^2}} \) \( = \frac{{8a\sqrt 7 }}{7}\).

Áp dụng định lí Pytago trong tam giác vuông \(OAH\) có:

\(AH = \sqrt {O{A^2} - O{H^2}} \)\( = \sqrt {{{\left( {3a} \right)}^2} - {{\left( {\frac{{6a\sqrt 7 }}{7}} \right)}^2}} \) \( = \frac{{3a\sqrt {21} }}{7}\).

\( \Rightarrow AB = 2AH = \frac{{6a\sqrt {21} }}{7}\).

Vậy diện tích tam giác \(SAB\) là: \({S_{\Delta SAB}} = \frac{1}{2}SH.AB\)\( = \frac{1}{2}.\frac{{8a\sqrt 7 }}{7}.\frac{{6a\sqrt {21} }}{7}\) \( = \frac{{24{a^2}\sqrt 3 }}{7}\). 

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

\( + \) Thiết diện qua trục là tam giác \(SMN \Rightarrow \widehat {MSN} = {120^0} \Rightarrow \widehat {OSN} = {60^0}\).

Ta có: \(SO = \dfrac{{ON}}{{\tan {{60}^0}}} = \dfrac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \)

\( + \)\(\left( {SAB} \right)\) tạo với đáy góc \({60^0} \Rightarrow \widehat {SHO} = {60^0}\)

\( + \)\(OH = \dfrac{{SO}}{{\tan {{60}^0}}} = \dfrac{{R\sqrt 3 }}{{\sqrt 3 }} = R.\)

+ Ta có:\(S{O^2} + O{H^2} = S{H^2} \Leftrightarrow {\left( {R\sqrt 3 } \right)^2} + {R^2} = S{H^2} \Leftrightarrow SH = 2R\)

\( + \)\(O{H^2} + H{B^2} = O{B^2} \Leftrightarrow H{B^2} = {\left( {3R} \right)^2} - {R^2} \Leftrightarrow HB = 2R\sqrt 2 \)

\( \Rightarrow AB = 2HB = 4R\sqrt 2 \)

\( + \)\({S_{\Delta SAB}} = \dfrac{1}{2}.SH.AB = \dfrac{1}{2}.2R.4R\sqrt 2  = 4\sqrt 2 .{R^2}\).

Chọn B

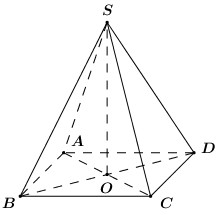
Phương pháp giải:

+ \(ABCD\) là hình vuông ngoại tiếp đường tròn đáy của hình nón. Tính độ dài cạnh hình vuông.

+ Gọi \(O\) là tâm hình vuông \(ABCD\), sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính \(SO\).

+ Sử dụng công thức \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\).

Lời giải chi tiết:

Gọi \(O\)là tâm hình vuông \(ABCD\).

Hình vuông \(ABCD\)có \(OA = OB = OC = OD = 2.\)

\( \Rightarrow AC = BD = 4 \Rightarrow AB = 2\sqrt 2 \).

Vì góc ở đỉnh của hình nón bằng \({120^0} \Rightarrow \angle BSD = {120^0} \Rightarrow \angle BSO = {60^0}.\)

Xét tam giác vuông \(SOB\) có: \(SO = OB.\cot {60^0} = 2.\dfrac{1}{{\sqrt 3 }} = \dfrac{{2\sqrt 3 }}{3}\).

Vậy \({V_{S.ABCD}} = \dfrac{1}{3}.SO.A{B^2} = \dfrac{1}{3}.\dfrac{{2\sqrt 3 }}{3}.{\left( {2\sqrt 2 } \right)^2} = \dfrac{{16\sqrt 3 }}{9}.\)

Chọn C.

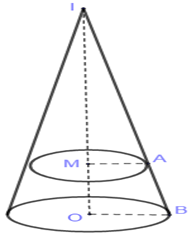
Phương pháp giải:

Thể tích khối nón được tính bởi công thức \(V = \dfrac{1}{3}\pi {r^2}h\) (trong đó \(r\) là bán kính đáy, \(h\) là chiều cao).

Lời giải chi tiết:

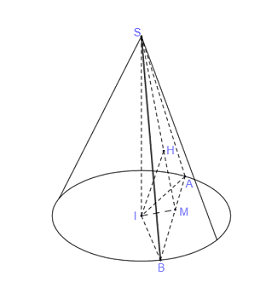
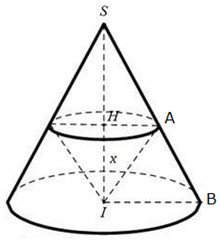
Giả sử có một đường sinh của hình nón cắt \(\left( P \right)\) tại \(A\) và cắt đáy tâm \(O\) tại \(B\).

Mặt phẳng \(\left( P \right)\) chia hình nón thành 2 phần trong đó có 1 phần là hình nón có đỉnh là \(I\), đáy là đường tròn tâm \(M\).

Đặt \(h = IO;\)\(r = OB;\)\({h_1} = IM;\)\({r_1} = MA\)

Do \(MA\parallel OB\) (cùng vuông góc với \(OI\)) nên áp dụng định lí Ta-lét: \(\dfrac{{IM}}{{IO}} = \dfrac{{MA}}{{OB}} \Leftrightarrow \dfrac{{{h_1}}}{h} = \dfrac{{{r_1}}}{r}\).

Thể tích khối nón ban đầu là: \(V = \dfrac{1}{3}\pi .O{B^2}.OI = \dfrac{1}{3}\pi {r^2}h\).

Thể tích khối nón có đỉnh \(I,\) đường tròn đáy có tâm \(M\) là: \({V_1} = \dfrac{1}{3}\pi M{A^2}.IM = \dfrac{1}{3}\pi {r_1}^2.{h_1}\)

Ta có: \(\dfrac{{{V_1}}}{V} = \dfrac{1}{2} \Leftrightarrow \dfrac{{\dfrac{1}{3}\pi {r_1}^2{h_1}}}{{\dfrac{1}{3}\pi {r^2}h}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{{r_1}^2{h_1}}}{{{r^2}h}} = \dfrac{1}{2} \Leftrightarrow {\left( {\dfrac{{{h_1}}}{h}} \right)^3} = \dfrac{1}{2} \Leftrightarrow \dfrac{{{h_1}}}{h} = \dfrac{1}{{\sqrt[3]{2}}}\).

Vậy \(\dfrac{{IM}}{{IO}} = \dfrac{{{h_1}}}{h} = \dfrac{1}{{\sqrt[3]{2}}}\).

Chọn B.

Phương pháp giải:

- Đặt \(IH = x\) lập công thức tính thể tích khối nón theo \(x\) .

- Sử dụng phương pháp hàm số đánh giá GTLN của thể tích.

Lời giải chi tiết:

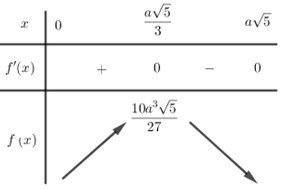
Tam giác \(SIB\) vuông tại \(I\) ta có \(SI = \sqrt {S{B^2} - I{B^2}}  = \sqrt {9{a^2} - 5{a^2}}  = 2a\).

Đặt \(IH = x\left( {0 < x < a\sqrt 5 } \right)\) \( \Rightarrow SH = SI - IH = a\sqrt 5  - x\)

Tam giác \(SHA\) đồng dạng \(SIB\) nên

\(\dfrac{{HA}}{{IB}} = \dfrac{{SH}}{{SI}} \Leftrightarrow \dfrac{{HA}}{{2a}} = \dfrac{{a\sqrt 5  - x}}{{a\sqrt 5 }}\) \( \Leftrightarrow HA = \dfrac{{2a\sqrt 5  - 2x}}{{\sqrt 5 }}\)

Thể tích khối nón đỉnh \(I\) đường tròn đáy tâm \(H\) là:

\(V = \dfrac{1}{3}\pi H{A^2}.IH\) \( = \dfrac{1}{3}\pi .{\left( {\dfrac{{2a\sqrt 5  - 2x}}{{\sqrt 5 }}} \right)^2}.x = \dfrac{{4\pi }}{{15}}{\left( {a\sqrt 5  - x} \right)^2}.x\)

Xét hàm \(f\left( x \right) = {\left( {a\sqrt 5  - x} \right)^2}.x\) trên \(\left( {0;a\sqrt 5 } \right)\) có:

\(\begin{array}{l}f'\left( x \right) =  - 2\left( {a\sqrt 5  - x} \right).x + {\left( {a\sqrt 5  - x} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, =  - 2ax\sqrt 5  + 2{x^2} + 5{a^2} - 2ax\sqrt 5  + {x^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - 4ax\sqrt 5  + 5{a^2}\end{array}\) 

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\sqrt 5 \left( {loai} \right)\\x = \dfrac{{a\sqrt 5 }}{3}\left( {TM} \right)\end{array} \right.\)

Bảng biến thiên:

Từ bảng biến thiên ta thấy hàm số \(f\left( x \right)\) đạt GTLN tại \(x = \dfrac{{a\sqrt 5 }}{3}\) và \(f\left( {\dfrac{{a\sqrt 5 }}{3}} \right) = \dfrac{{10{a^3}\sqrt 5 }}{{27}}\)

Vậy thể tích lớn nhất \({V_{\max }} = \dfrac{{4\pi }}{{15}}.\dfrac{{10{a^3}\sqrt 5 }}{{27}} = \dfrac{{8\pi {a^3}\sqrt 5 }}{{81}}\).

Chọn C

Phương pháp giải:

Lời giải chi tiết:

+ Thiết diện qua trục là\(\Delta ABC\)vuông cân tại \(A\) có \(BC = 2a\)

\( \Rightarrow R = \dfrac{1}{2}BC = \dfrac{1}{2}.2a = a.\)

+ Gọi \(O\) là trung điểm \(BC\).

+ \(h = AO = \dfrac{1}{2}BC = a\) (tam giác vuông có đường trung tuyến bằng nửa cạnh huyền).

\( \Rightarrow \) \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a = \dfrac{{\pi {a^3}}}{3}\).

Chọn B

Phương pháp giải:

Lời giải chi tiết:

+ Thiết diện qua trục là tam giácvuông cân

\( \Rightarrow \left\{ \begin{array}{l}SA = SB = a\\AB = a\sqrt 2 \\SO = \dfrac{{AB}}{2} = \dfrac{{a\sqrt 2 }}{2}\\{r_{day}} = OA = \dfrac{{AB}}{2} = \dfrac{{a\sqrt 2 }}{2}\end{array} \right.\)

\( + \) Thiết diện qua đỉnh tạo với đáy \({60^0} \Rightarrow \widehat {SHO} = {60^0}\)

\( + \)\(\tan \widehat {SHO} = \tan {60^0} \Leftrightarrow \dfrac{{SO}}{{OH}} = \sqrt 3  \Leftrightarrow OH = \dfrac{{SO}}{{\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{6}\)

\( + \)\(\sin \widehat {SHO} = \sin {60^0} \Leftrightarrow \dfrac{{SO}}{{SH}} = \dfrac{{\sqrt 3 }}{2} \Leftrightarrow SH = \dfrac{{a\sqrt 6 }}{3}\).

\( + \) Xét \(\Delta OMH\) vuông tại \(H\) có:

\(\begin{array}{l}O{H^2} + M{H^2} = O{M^2} \Leftrightarrow M{H^2} = {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} - {\left( {\dfrac{{a\sqrt 6 }}{6}} \right)^2}\\ \Leftrightarrow MH = \dfrac{{a\sqrt 3 }}{3} \Leftrightarrow MN = 2MH = \dfrac{{2a\sqrt 3 }}{3}\end{array}\)

\( + \)\({S_{\Delta SMN}} = \dfrac{1}{2}.SH.MN = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{2a\sqrt 3 }}{3} = \dfrac{{{a^2}\sqrt 2 }}{3}\).

Chọn B

Phương pháp giải:

Lời giải chi tiết:

\( + \)\(\left( {SAB} \right)\) tạo với đáy một góc \({45^0} \Rightarrow \widehat {SHO} = {45^0}\)

\( \Rightarrow \Delta SHO\) vuông cân tại \(O\) \( \Rightarrow \left\{ \begin{array}{l}SO = OH = a\\SH = a\sqrt 2 \end{array} \right.\)

\( + \)\(\Delta OAB\) vuông cân tại \(O\) có đường cao \(OH\).

\( \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} \Leftrightarrow \dfrac{1}{{{a^2}}} = \dfrac{1}{{{r^2}}} + \dfrac{1}{{{r^2}}} \Leftrightarrow \dfrac{2}{{{r^2}}} = \dfrac{1}{{{a^2}}} \Leftrightarrow r = a\sqrt 2 \)

\( + \)\({V_{non}} = \dfrac{1}{3}.\pi .{r^2}.SO = \dfrac{1}{3}\pi .{\left( {a\sqrt 2 } \right)^2}.a = \dfrac{{2\pi {a^3}}}{3}.\)

 Chọn A

Phương pháp giải:

Lời giải chi tiết:

\( + \)Khoảng cách từ tâm đáy đến thiết diện: \(d\left( {O;\left( {SAB} \right)} \right)\)

+ Kẻ \(OH \bot AB\) (\(H\) trung điểm \(AB\))

\(OK \bot SH\)

\( \Rightarrow d\left( {O,SAB} \right) = OK = 12\)

\( + \)\(\Delta SHO\) vuông tại \(O\) có đường cao \(OK\).

\(\begin{array}{l} \Rightarrow \dfrac{1}{{O{K^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{H^2}}} \Leftrightarrow \dfrac{1}{{{{12}^2}}} = \dfrac{1}{{{{20}^2}}} + \dfrac{1}{{O{H^2}}}\\ \Leftrightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{225}} \Leftrightarrow OH = 15\left( {cm} \right)\end{array}\)

\( + \)\(\Delta OHB\)vuông tại \(H\) có:

\(O{H^2} + B{H^2} = O{B^2} \Leftrightarrow B{H^2} = {25^2} - {15^2} \Leftrightarrow BH = 20\left( {cm} \right)\).

\( \Rightarrow AB = 2BH = 40\,\,\left( {cm} \right)\)

\( + \)\(S{H^2} = S{O^2} + O{H^2} = {20^2} + {15^2} = {25^2}\) \( \Leftrightarrow SH = 25\left( {cm} \right)\)

\( + \)\({S_{\Delta SAB}} = \dfrac{1}{2}.SH.AB = \dfrac{1}{2}.25.40 = 500\left( {c{m^2}} \right)\).

Chọn A

Phương pháp giải:

Lời giải chi tiết:

+ Gọi \(D\) là trung điểm của \(BC\).

+ Gọi \(O\) là tâm đường tròn ngoại tiếp \(\Delta ABC \Rightarrow SO \bot \left( {ABC} \right)\).

+ Hình nón ngoại tiếp chóp \(S.ABCD\) có\(\left\{ \begin{array}{l}R = OA\\h = SO\end{array} \right.\)

+ \(\Delta ABC\) đều cạnh cạnh 3 \( \Rightarrow \)\(AD = \dfrac{{3\sqrt 3 }}{2} \Rightarrow AO = \dfrac{2}{3}.AD \Rightarrow AO = \sqrt 3 \)

+ Xét\(\Delta SAO\) vuông tại \(O\) có: \(S{A^2} = S{O^2} + A{O^2}\)

\( \Rightarrow S{O^2} = {4^2} - {\left( {\sqrt 3 } \right)^2} = 13 \Rightarrow SO = \sqrt {13} \)

+ \({V_{non}} = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}.3\pi .\sqrt {13}  = \sqrt {13} \pi .\)

Chọn C

Phương pháp giải:

Lời giải chi tiết:

Ta có \({R_{tron}} = {l_{non}}\)

Chu vi nửa hình tròn = Chu vi đáy hình nón

\( \Rightarrow \pi {R_{tron}} = 2\pi {R_{non}} \Leftrightarrow {R_{non}} = \dfrac{{{R_{tron}}}}{2}\)

\(\begin{array}{l}{h_{non}} = \sqrt {{l_{non}}^2 - {r_{non}}^2} \\\,\,\,\,\,\,\,\,\, = \sqrt {{R_{tron}}^2 - {{\left( {\dfrac{{{R_{tron}}}}{2}} \right)}^2}}  = \dfrac{{\sqrt 3 {R_{tron}}}}{2}\\{V_{non}} = \dfrac{1}{3}\pi .{r^2}.h = \dfrac{1}{3}\pi .{\left( {\dfrac{{{R_{tron}}}}{2}} \right)^2}.\dfrac{{\sqrt 3 {R_{tron}}}}{2} = \dfrac{{\pi {R^3}_{tron}\sqrt 3 }}{{24}}\end{array}\)

Chọn B

Phương pháp giải:

Lời giải chi tiết:

Thiết diện qua trục là \(\Delta ABC\)đều cạnh \(a\):                                                        

\( \Rightarrow \)\(\left\{ \begin{array}{l}l = a\\h = \dfrac{{a\sqrt 3 }}{2}\\R = \dfrac{a}{2}\end{array} \right. \Rightarrow {V_{non}} = \dfrac{1}{3}\pi {R^2}.h = \dfrac{{\pi {a^3}\sqrt 3 }}{{24}}\)

Chọn C

Phương pháp giải:

Lời giải chi tiết:

+ Gọi \(H\) là trung điểm \(CD\).

+ \(O\) là trọng tâm \(\Delta BCD\)\( \Rightarrow AO \bot \left( {BCD} \right)\).

+ Hình nón ngoại tiếp tứ diện đều có \(\left\{ \begin{array}{l}R = OB\\l = AB = a\end{array} \right.\)

+\(\Delta BCD\) đều cạnh \(a \Rightarrow BH = \dfrac{{a\sqrt 3 }}{2}\).

Mà \(BO = \dfrac{2}{3}BH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3} \Rightarrow R = \dfrac{{a\sqrt 3 }}{3}\)

+ \({S_{xq}} = \pi Rl = \pi .BO.BA = \pi .\dfrac{{a\sqrt 3 }}{3}.a = \dfrac{{\pi {a^2}\sqrt 3 }}{3}\).

Chọn D

Phương pháp giải:

- Tính \(AH,\,\,CH\) theo \(R\) và \(\alpha \).

- Thể tích khối nón có đường cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

- Sử dụng phương pháp hàm số để tìm GTLN của hàm số.

Lời giải chi tiết:

Khi quay tam giác vuông \(ACH\) quanh trục \(AB\) ta nhận được khối nón có chiều cao \(h = AH\), bán kính đáy \(r = CH\).

Ta có \(\angle ACB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta ABC\) vuông tại \(C\).

\( \Rightarrow AC = AB.\cos \alpha  = 2R\cos \alpha \).

\( \Rightarrow AH = AC.\cos \alpha  = 2R\cos \alpha .cos\alpha  = 2Rco{s^2}\alpha \), \(CH = AC.\sin \alpha  = 2R\cos \alpha \sin \alpha \).

Thể tích khối nón tạo thành là:

\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {\left( {2R\cos \alpha sin\alpha } \right)^2}.2R{\cos ^2}\alpha \)

    \( = \dfrac{{8\pi }}{3}{R^3}{\cos ^4}\alpha {\sin ^2}\alpha \)\( = \dfrac{{8\pi {R^3}}}{3}{\cos ^4}\alpha \left( {1 - {{\cos }^2}\alpha } \right)\).

Đặt \(t = {\cos ^2}\alpha \), do \(0 < \alpha  < {90^0}\) nên \(0 < t < 1\).

Khi đó \({\cos ^4}\alpha \left( {1 - {{\cos }^2}\alpha } \right) = {t^2}\left( {1 - t} \right)\).

Xét hàm số \(f\left( t \right) = {t^2}\left( {1 - t} \right) = {t^2} - {t^3}\) với \(0 < t < 1\) ta có: \(f'\left( t \right) = 2t - 3{t^2}\)

\(f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \dfrac{2}{3}\end{array} \right.\)

BBT:

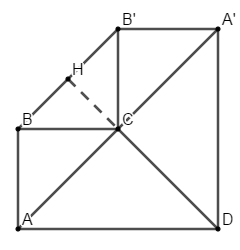
Từ BBT suy ra \({V_{\max }} \Leftrightarrow t = \dfrac{2}{3}\)

\( \Rightarrow {\cos ^2}\alpha  = \dfrac{2}{3}\)\( \Leftrightarrow 1 + {\tan ^2}\alpha  = \dfrac{1}{{{{\cos }^2}\alpha }} = \dfrac{3}{2}\)\( \Leftrightarrow {\tan ^2}\alpha  = \dfrac{1}{2}\)\( \Leftrightarrow \tan \alpha  = \dfrac{1}{{\sqrt 2 }}\) (Do \(0 < \alpha  < {90^0}\) nên \(\tan \alpha  > 0\))

Vậy \(\alpha  = \arctan \dfrac{1}{{\sqrt 2 }}\).

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Gọi \(M,\,\,N,\,\,P,\,\,Q\) lần lượt là tâm các hình vuông \(ABB'A'\), \(ADD'A'\), \(CDD'C'\), \(BCC'B'\).

Khi đó \(\left( H \right)\)  là khối bát diện đều \(OMNPQO'\) cạnh bằng \(\dfrac{{a\sqrt 2 }}{2}\) \( \Rightarrow {V_{\left( H \right)}} = \dfrac{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^3}\sqrt 2 }}{3} = \dfrac{{{a^3}}}{6}\).

Thể tích khối lập phương là \({a^3}\).

\( \Rightarrow {V_1} = {a^3} - \dfrac{{{a^3}}}{6} = \dfrac{{5{a^3}}}{6}\).

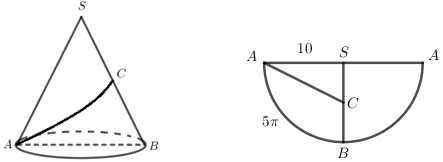
Khối nón \(\left( N \right)\) có đỉnh và tâm đáy lần lượt là \(O,\,\,O'\) \( \Rightarrow OO'\) là đường cao của khối nón.

\( \Rightarrow \) Mặt đáy của khối nón vuông góc với \(OO'\).

Mà \(OO' \bot \left( {MNPQ} \right)\) nên \(\left( {MNPQ} \right)\) song song với mặt đáy của khối nón \(\left( N \right)\).

Qua \(O\) dựng mặt phẳng song song với \(\left( {MNPQ} \right)\), gọi \(M',\,\,N',\,\,P',\,\,Q'\) lần lượt là giao điểm của \(OM,\,\,ON,\,\,OP,\,\,OQ\) với mặt đáy của khối nón \(\left( N \right)\).

Khi đó khối nón \(\left( N \right)\) là khối nón ngoại tiếp chóp \(O.M'N'P'Q'\).

Ta có \(MNPQ\) là hình vuông cạnh \(\dfrac{{a\sqrt 2 }}{2}\) nên \(MP = \dfrac{{a\sqrt 2 }}{2}.\sqrt 2  = a\).

\(MP\) là đường trung bình của tam giác \(OM'P'\) nên \(M'P' = 2MP = 2a\).

\( \Rightarrow \) Bán kính đáy khối nón \(\left( N \right)\) là \(r = \dfrac{1}{2}M'P' = a\). Ta có \(OO' = AA' = a\).

\( \Rightarrow {V_2} = \dfrac{1}{3}\pi .{a^2}.a = \dfrac{{\pi {a^3}}}{3}\).

Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{5{a^3}}}{6}:\dfrac{{\pi {a^3}}}{3} = \dfrac{5}{{2\pi }}\)  

Chọn C.

Phương pháp giải:

- Trải phẳng mặt nón cắt mép \(SA\).

- Tính góc ở tâm chắn cung \(AB\) và suy ra độ dài \(AC\) min.

Lời giải chi tiết:

Độ dài cung \(AB\) là \(\frac{{2\pi R}}{2} = \pi R = 5\pi \)

Có \(5\pi  = 10.\angle ASC \Rightarrow \angle ASC = \frac{\pi }{2}\). Do đó \(A{C_{\min }} = \sqrt {S{A^2} + S{C^2}}  = \sqrt {{{10}^2} + {5^2}}  = 5\sqrt 5 \).

Chọn D.