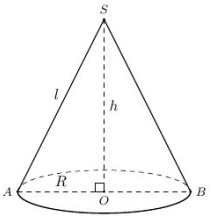
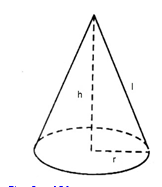
40 bài tập trắc nghiệm mặt nón mức độ nhận biếtLàm bàiCâu hỏi 1 : Cho khối nón có bán kính đáy là \(r\) và đường cao là \(h\). Thể tích của khối nón bằng
Đáp án: A Phương pháp giải: Thể tích của khối nón có bán kính đáy là \(r\) và đường cao là \(h\) là: \(\dfrac{1}{3}\pi {r^2}h\). Lời giải chi tiết: Thể tích của khối nón có bán kính đáy là \(r\) và đường cao là \(h\) là: \(\dfrac{1}{3}\pi {r^2}h\). Chọn A. Câu hỏi 2 : Diện tích xung quanh của hình nón có bán kính đường tròn đáy \(R\) và chiều cao \(h\) bằng:
Đáp án: B Phương pháp giải: - Tính đường sinh của hình nón \(l = \sqrt {{R^2} + {h^2}} \). - Áp dụng công thức tính diện tích xung quanh của hình nón có bán kính đáy \(R\), đường sinh \(l\)là \({S_{xr}} = \pi Rl\). Lời giải chi tiết: Hình nón có bán kính đáy R và chiều cao h thì đường sinh \(l = \sqrt {{R^2} + {h^2}} \). Khi đó diện tích xung quanh hình nón là \({S_{xq}} = \pi Rl = \pi R\sqrt {{R^2} + {h^2}} \). Chọn B. Câu hỏi 3 : Cho hình nón có bán kính đường tròn đáy bằng \(R,\) chiều cao bằng \(h,\) độ dài đường sinh bằng \(l.\) Khẳng định nào sau đây đúng?
Đáp án: B Phương pháp giải: Hình nón có bán kính đáy \(R,\) chiều cao \(h\) và đường sinh \(l\) thì ta có: \({l^2} = {h^2} + {R^2}.\) Lời giải chi tiết:
Hình nón có bán kính đáy \(R,\) chiều cao \(h\) và đường sinh \(l\) thì ta có: \({l^2} = {h^2} + {R^2}.\) \( \Rightarrow l = \sqrt {{R^2} + {h^2}} .\) Chọn B. Câu hỏi 4 : Cho hình nón có bán kính đáy \(r = \sqrt 3 ,\) độ dài đường sinh \(l = 4.\) Tính diện tích xung quanh của hình nón đó?
Đáp án: B Phương pháp giải: Diện tích xung quanh của hình nón bán kính đáy \(R\) và đường sinh \(l\) là: \({S_{xq}} = \pi Rl.\) Lời giải chi tiết: Diện tích xung quanh của hình nón đã cho là: \({S_{xq}} = \pi Rl = \pi .\sqrt 3 .4 = 4\sqrt 3 \pi .\) Chọn B. Câu hỏi 5 : Diện tích xung quanh của hình nón có chiều cao \(h\), độ dài đường sinh \(l\), bán kính đáy \(r\) bằng:
Đáp án: A Phương pháp giải: Diện tích xung quanh của hình nón có chiều cao \(h\), độ dài đường sinh \(l\), bán kính đáy \(r\) bằng: \({S_{xq}} = \pi rl\). Lời giải chi tiết: Diện tích xung quanh của hình nón có chiều cao \(h\), độ dài đường sinh \(l\), bán kính đáy \(r\) bằng: \({S_{xq}} = \pi rl\). Chọn A. Câu hỏi 6 : Cho hình nón có chiều cao \(h = 4,\) bán kính đáy \(r = 3.\) Diện tích xung quanh của hình nón đã cho bằng:
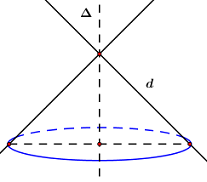
Đáp án: C Phương pháp giải: Diện tích xung quanh của hình nón bán kính đáy \(R\) và chiều cao \(h\) là \({S_{xq}} = \pi Rl = \pi R.\sqrt {{h^2} + {R^2}} .\) Lời giải chi tiết: Diện tích xung quanh của hình nón đã cho là: \({S_{xq}} = \pi Rl = \pi .3.\sqrt {{4^2} + {3^2}} = 15\pi .\) Chọn C. Câu hỏi 7 : Cho hai đường thẳng \(d\) và \(\Delta \) cắt nhau nhưng không vuông góc với nhau. Mặt tròn xoay sinh bởi đường thẳng \(d\) khi quay quanh \(\Delta \) là:
Đáp án: D Phương pháp giải: Dựa vào lý thuyết về khối tròn xoay. Lời giải chi tiết: Mặt tròn xoay sinh bởi đường thẳng \(d\) khi quay quanh \(\Delta \) với \(d\) và \(\Delta \) là hai đường thẳng cắt nhau nhưng không vuông góc ta được một khối nón tròn xoay.
Chọn D. Câu hỏi 8 : Cho khối nón có chiều cao h và đường kính đường tròn đáy là a. Thể tích của khối nón đã cho bằng:
Đáp án: A Phương pháp giải: Thể tích khối nón có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \dfrac{1}{3}\pi {R^2}h.\) Lời giải chi tiết: Bán kính đường tròn đáy của khối nón đã cho là: \(R = \dfrac{a}{2}.\) \( \Rightarrow \) Thể tích của khối nón đã cho là:\(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {\left( {\dfrac{a}{2}} \right)^2}.h = \dfrac{1}{{12}}\pi {a^2}h.\) Chọn A. Câu hỏi 9 : Cho hình nón có thiết diện qua trục là tam giác đều cạnh bằng \(2a\) . Diện tích xung quanh của hình nón bằng
Đáp án: A Phương pháp giải: - Dựa vào thiết diện qua trục xác định đường sinh \(l\) và bán kính \(r\) của hình nón. - Diện tích xung quanh của hình nón có đường sinh \(l\) và bán kính \(r\) là \({S_{xq}} = \pi rl\). Lời giải chi tiết:
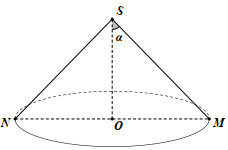
Vì thiết diện qua trục là tam giác đều cạnh \(2a\) nên hình nón có đường sinh \(l = 2a\) và bán kính đáy \(r = a\). Vậy diện tích xung quanh của hình nón là \({S_{xq}} = \pi rl = \pi .a.2a = 2\pi {a^2}\). Chọn A. Câu hỏi 10 : Cho hình nón có bán kính đáy R, góc ở đỉnh là \(2\alpha \) với \({45^0} < \alpha < {90^0}\). Tính diện tích xung quanh của hình nón theo R và \(\alpha \).
Đáp án: C Phương pháp giải: - Dựa vào thiết diện qua trục xác định đường sinh \(l\) và bán kính \(r\) của hình nón. - Diện tích xung quanh của hình nón có đường sinh \(l\) và bán kính \(r\) là \({S_{xq}} = \pi rl\). Lời giải chi tiết:
Theo bài ra ta có: \(\angle NSM = 2\alpha \Rightarrow \angle OSM = \alpha \). Xét tam giác vuông SOM ta có: \(l = SM = \dfrac{{OM}}{{\sin \alpha }} = \dfrac{R}{{\sin \alpha }}\). Vậy diện tích xung quanh của hình nón là \({S_{xq}} = \pi .R.\dfrac{R}{{\sin \alpha }} = \dfrac{{\pi {R^2}}}{{\sin \alpha }}\). Chọn C. Câu hỏi 11 : Tính diện tích xung quanh của hình nón có đường sinh bằng 2, bán kính đáy bằng 1.
Đáp án: A Phương pháp giải: Công thức tính diện tích xung quanh hình nón có bán kính đáy \(R,\;\)chiều cao \(h\) và đường sinh \(l:\;\) \(\;{S_{xq}} = \pi Rl = \pi R\sqrt {{h^2} + {R^2}} .\) Lời giải chi tiết: Diện tích xung quanh của hình nón có đường sinh bằng 2, bán kính đáy bằng 1 là: \({S_{xq}} = \pi Rl = \pi .2.1 = 2\pi .\) Chọn A. Câu hỏi 12 : Cho hình nón có chiều cao \(h = 4cm\), bán kính đáy \(r = 3cm\). Độ dài đường sinh của hình nón là
Đáp án: A Phương pháp giải: Gọi \(h,\,\,r,\,\,l\) lần lượt là đường cao, bán kính đáy và độ dài đường sinh của hình nón, khi đó \(l = \sqrt {{h^2} + {r^2}} \). Lời giải chi tiết: Độ dài đường sinh của hình nón là \(l = \sqrt {{h^2} + {r^2}} = \sqrt {{4^2} + {3^2}} = 5\,\,\left( {cm} \right).\) Chọn A. Câu hỏi 13 : Cho hình nón có diện tích xung quanh bằng \(6\pi {a^2}\) và đườngkính đáy bằng \(2a\). Tính độ dài đường sinh hình nón đã cho.
Đáp án: C Phương pháp giải: Diện tích xung quanh của hình nón có bán kính đáy \(r\) và đường sinh \(l\) là: \({S_{xq}} = \pi rl\). Lời giải chi tiết: Bán kính đáy của hình nón là \(r = \dfrac{{2a}}{2} = a\). Diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl\) \( \Leftrightarrow 6\pi {a^2} = \pi .a.l \Leftrightarrow l = 6a\). Vậy độ dài đường sinh của hình nón đã cho là \(6a\). Chọn C. Câu hỏi 14 : Cho tam giác ABC vuông tại \(A,\,\,AB = c,\,\,AC = b.\) Quay tam giác \(ABC\) xung quanh đường thẳng chứa cạnh \(AB\) ta được một hình nón có thể tích bằng :
Đáp án: D Phương pháp giải: Thể tích khối nón có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \frac{1}{3}\pi {R^2}h.\) Lời giải chi tiết: Khi quay \(\Delta ABC\) vuông tại \(A\) quanh đường thẳng chứa cạnh \(AB\) ta được hình nón có đường cao \(h = AB = c,\) bán kính đáy \(r = AC = b.\) Khi đó thể tích khối nón được tạo thành là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {b^2}c.\) Chọn D. Câu hỏi 15 : Diện tích xung quanh \({S_{xq}}\) của hình nón có bán kính đáy \(R = a\) và đường sinh \(l = a\sqrt 2 \) là :
Đáp án: C Phương pháp giải: Diện tích xung quanh hình nón \({S_{xq}} = \pi Rl\). Lời giải chi tiết: Diện tích xung quanh hình nón \({S_{xq}} = \pi Rl\)\( = \pi .a.a\sqrt 2 = \pi {a^2}\sqrt 2 \). Chọn C. Câu hỏi 16 : Nếu một khối nón có bán kính đường tròn đáy và độ dài đường cao cùng bằng \(3a\) thì có thể tích bằng
Đáp án: D Phương pháp giải: Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\). Lời giải chi tiết: Ta có: \(r = h = 3a\). Vậy thể tích khối nón là: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {\left( {3a} \right)^2}.3a = 9\pi {a^3}\). Đáp án D. Câu hỏi 17 : Cho khối nón có bán kính đáy \(r = \sqrt 2 \), chiều cao \(h = 2\sqrt 3 \). Thể tích của khối nón là:
Đáp án: A Phương pháp giải: Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là: \(V = \frac{1}{3}\pi {r^2}h\). Lời giải chi tiết: Thể tích khối nón là \(V = \frac{1}{3}\pi .{\left( {\sqrt 2 } \right)^2}.2\sqrt 3 = \frac{{4\pi \sqrt 3 }}{3}\). Chọn A. Câu hỏi 18 : Cho hình nón có bán kính đường tròn đáy \(r = 3a\) và đường sinh \(l = 2r.\) Diện tích xung quanh của hình nón bằng
Đáp án: D Phương pháp giải: Diện tích xung quanh hình nón \({S_{xq}} = \pi rl\). Lời giải chi tiết: Diện tích xung quanh hình nón \({S_{xq}} = \pi rl\)\( = \pi .\left( {3a} \right).\left( {2.3a} \right) = 18\pi {a^2}\). Chọn D. Câu hỏi 19 : Cho khối nón có bán kính đáy \(r = 3\) và chiều cao \(h = 5\). Tính thể tích \(V\) của khối nón đã cho
Đáp án: D Phương pháp giải: Thể tích của khối nón được tính bởi công thức \(V = \dfrac{1}{3}\pi {r^2}h\) (\(r\) là bán kính đáy, \(h\) là chiều cao). Lời giải chi tiết: Thể tích \(V\) của khối nón có bán kính đáy \(r = 3\) và chiều cao \(h = 5\) là: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.3^2}.5 = 15\pi .\) Chọn D. Câu hỏi 20 : Một dụng cụ đựng chất lỏng có dạng hình nón với chiều cao là 30cm và bán kính đáy là 15cm. Dụng cụ này đựng được tối đa bao nhiêu cm3 chất lỏng?
Đáp án: A Phương pháp giải: Thể tích khối nón chiều cao \(h\), bán kính đáy \(r\) là \(V = \frac{1}{3}\pi {r^2}h\). Lời giải chi tiết: Khối nón có chiều cao cao \(h = 30cm\) và bán kính đáy \(r = 15cm\) có thể tích là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.15^2}.30 = 2250\pi \,\,\left( {c{m^3}} \right)\). Chọn A. Câu hỏi 21 : Cho một hình nón đỉnh S và AB là một đường kính của đường tròn đáy. Nếu tam giác \(SAB\) đều thì góc ở đỉnh của hình nón bằng
Đáp án: B Phương pháp giải: Thể tích khối chóp \(V = \frac{1}{3}{S_{day}}.h\). Lời giải chi tiết: Hình nón đỉnh \(S\) có \(AB\) là một đường kính của đường tròn đáy nên góc ở đỉnh của hình nón là \(\angle ASB\). Lại có \(\Delta SAB\) đều nên \(\angle ASB = {60^0}\). Vậy góc ở đỉnh của hình nón bằng \({60^0}\). Chọn B. Câu hỏi 22 : Cho hình nón có diện tích xung quanh bằng \(5\pi {a^2}\)và bán kính đường tròn đáy bằng \(a\) . Độ dài đường sinh của hình nón đã cho là:
Đáp án: A Phương pháp giải: Diện tích xung quanh của hình nón bằng \(\pi rl\)(\(r\) là bán kính, \(l\) là đường sinh). Lời giải chi tiết: Gọi \(l\) là độ dài đường sinh của hình nón ta có: \(5\pi {a^2} = \pi al \Leftrightarrow l = 5a\). Chọn A. Câu hỏi 23 : Cho hình nón có diện tích xung quanh bằng \(5\pi {a^2}\) và bán kính đáy bằng \(a\). Tính độ dài đường sinh của hình nón đã cho?
Đáp án: D Phương pháp giải: Diện tích xung quanh của hình nón là \({S_{xq}} = \pi rl\) (\(r\) là bán kính đáy; \(l\) là đường sinh của hình nón). Lời giải chi tiết: Theo giả thiết, diện tích xung quanh của hình nón bằng \(5\pi {a^2}\) và bán kính đáy bằng \(a\) nên \(\left\{ \begin{array}{l}\pi rl = 5\pi {a^2}\\r = a\end{array} \right. \Rightarrow l = 5a.\) Vậy đường sinh của khối nón bằng \(5a.\) Chọn D. Câu hỏi 24 : Cho khối nón có chiều cao \(h = 9a\) và bán kính đường tròn đáy \(r = 2a.\) Thể tích của khối nón đã cho là
Đáp án: A Phương pháp giải: Thể tích khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\) . Lời giải chi tiết: Thể tích khối nón: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi .{\left( {2a} \right)^2}.9a = 12\pi {a^3}\). Chọn A Câu hỏi 25 : Quay hình nào dưới đây xung quanh trục đã chỉ ra cho ta một khối nón tròn xoay?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Xoay 1 tam giác cân quanh trục đối xứng (đường cao) của nó, ta được một khối nón.
Chọn A Câu hỏi 26 : Thể tích khối nón có chiều cao bằng 2, bán kính hình tròn đáy bằng 5 là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Chọn C Câu hỏi 27 : Cho hình nón có đường cao và đường kính đáy cùng bằng\(2a\). Cắt hình nón đã cho bởi một mặt phẳng qua trục, diện tích thiết diện bằng:
Đáp án: C Phương pháp giải: \({S_\Delta } = \dfrac{1}{2}a{h_a}\) trong đó \(a\) là cạnh của tam giác, \({h_a}\) là chiều cao ứng với cạnh \(a\). Lời giải chi tiết: Thiết diện qua trục là một tam giác cân có chiều cao \(h = 2a\), cạnh đáy bằng \(2a\). Khi đó \({S_{TD}} = \dfrac{1}{2}.2a.2a = 2{a^2}\). Chọn C Câu hỏi 28 : Cho khối nón có bán kính đáy \(r = \sqrt 3 \) và chiều cao \(h = 4.\) Thể tích của khối nón đã cho bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chọn B. Câu hỏi 29 : Cho khối nón có độ dài đường sinh bằng đường kính đáy bằng \(a.\) Thể tích khối nón là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Chọn C. Câu hỏi 30 : Cho hình nón có thể tích bằng \(12\pi \) và diện tích xung quanh bằng \(15\pi \). Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
Đáp án: B Phương pháp giải: Hình nón: \(V = \dfrac{1}{3}\pi {R^2}h,\,\,\,{S_{xq}} = \pi Rl\). Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}V = \dfrac{1}{3}\pi {R^2}h = 12\pi \\{S_{xq}} = \pi Rl = 15\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}h = \dfrac{{36}}{{{R^2}}}\\l = \dfrac{{15}}{R}\end{array} \right.\) Do \({R^2} = {l^2} - {h^2}\) nên \({R^2} = {\left( {\dfrac{{15}}{R}} \right)^2} - {\left( {\dfrac{{36}}{{{R^2}}}} \right)^2} \Leftrightarrow {R^6} - 225{R^2} + 1296 = 0 \Leftrightarrow R = 3\). Chọn: B Câu hỏi 31 : Hình nón có bán kính đáy, chiều cao, đường sinh lần lượt là \(r,h,l\). Diện tích xung quanh của hình nón là:
Đáp án: D Phương pháp giải: Diện tích xung quanh của hình nón là: \(S = \pi rl\). Lời giải chi tiết: Diện tích xung quanh của hình nón là: \(S = \pi rl\). Chọn: D Câu hỏi 32 : Khi quay một tam giác vuông (kể cả các điểm trong của tam giác vuông đó) quanh đường thẳng chứa một cạnh góc vuông ta được
Đáp án: C Phương pháp giải: Sử dụng kiến thức lý thuyết về khối nón. Lời giải chi tiết: Khi quay một tam giác vuông (kể cả các điểm trong của tam giác vuông đó) quanh đường thẳng chứa một cạnh góc vuông ta được một khối nón. Chọn C. Câu hỏi 33 : Cho hình nón có bán kính đáy bằng \(a\) và độ dài đường sinh bằng \(2a\). Diện tích xung quanh hình nón đó bằng:
Đáp án: A Phương pháp giải: Diện tích xung quanh của hình nón có bán kính đáy \(R\) và đường sinh \(l\) là: \({S_{xq}} = \pi Rl\) Lời giải chi tiết: Diện tích xung quanh hình nón đó bằng: \({S_{xq}} = \pi .a.2a = 2\pi {a^2}\). Chọn A Câu hỏi 34 : Thể tích của khối nón tròn xoay có đường kính đáy bằng 6 và chiều cao bằng 5 là
Đáp án: D Phương pháp giải: Thể tích khối nón là \(V=\dfrac{1}{3}\pi {{R}^{2}}h\) trong đó \(R;h\) lần lượt là bán kính đáy và chiều cao khối nón. Lời giải chi tiết: Ta có \(V=\dfrac{1}{3}\pi {{R}^{2}}h=\dfrac{1}{3}\pi {{.3}^{2}}.5=15\pi \). Chọn D. Câu hỏi 35 : Cho tam giác đều\(ABC\)có cạnh bằng\(a\)và đường cao AH. Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC quanh trục AH.
Đáp án: D Phương pháp giải: Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\) (Trong đó, r: bán kính đáy, l: độ dài đường sinh, h: độ dài đường cao). Lời giải chi tiết: Bán kính đáy: \(r = \dfrac{{BC}}{2} = \dfrac{a}{2}\) Diện tích xung quanh của hình nón đó là: \({S_{xq}} = \pi rl = \pi .\dfrac{a}{2}.a = \dfrac{{\pi {a^2}}}{2}\). Chọn: D Câu hỏi 36 : Cho đường thẳng \(\Delta \). Xét một đường thẳng \(l\) cắt \(\Delta \) tại một điểm. Mặt tròn xoay sinh bởi đường thẳng \(l\) khi quay quanh đường thẳng \(\Delta \) được gọi là:
Đáp án: B Phương pháp giải: Sử dụng khái niệm mặt nón: Mặt tròn xoay sinh bởi đường thẳng \(l\) cắt \(\Delta \) khi xoay quanh \(\Delta \) được gọi là mặt nón tròn xoay. Lời giải chi tiết: Cho đường thẳng \(\Delta \). Xét một đường thẳng \(l\) cắt \(\Delta \) tại một điểm. Mặt tròn xoay sinh bởi đường thẳng \(l\) khi quay quanh đường thẳng \(\Delta \) được gọi là mặt nón. Chọn B. Câu hỏi 37 : Cho hình nón có đường sinh \(l = 5cm\) và bán kính đáy \(r = 4cm\). Diện diện tích xung quanh của hình nón bằng:
Đáp án: D Phương pháp giải: Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi rl\) trong đó r, l lần lượt là bán kính đáy và độ dài đường sinh của hình nón. Lời giải chi tiết: Ta có \({S_{xq}} = \pi rl = \pi .4.5 = 20\pi \,\,\left( {c{m^2}} \right)\). Chọn D. Câu hỏi 38 : Cho hình nón có bán kính đáy bằng \(4a\) , chiều cao bằng \(3a.\) Diện tích xung quanh của hình nón bằng
Đáp án: A Phương pháp giải: Công thức tính diện tích xung quanh hình nón có bán kính đáy \(R,\;\) chiều cao \(h\) và đường sinh \(l:\;\;{S_{xq}} = \pi Rl.\) Lời giải chi tiết: Ta có: \(\;{S_{xq}} = \pi Rl = \pi R\sqrt {{h^2} + {R^2}} = \pi .4a\sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 20\pi {a^2}.\) Chọn A. Câu hỏi 39 : Tính thể tích V của khối nón của chiều cao \(h = a\) và bán kính đáy \(r = a\sqrt 3 .\)
Đáp án: A Phương pháp giải: Thể tích khối nón có bán kính đáy r và chiều cao h là: \(V = \dfrac{1}{3}\pi {r^2}h.\) Lời giải chi tiết: Ta có: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi .{\left( {a\sqrt 3 } \right)^2}.a = \pi {a^3}.\) Chọn A. Câu hỏi 40 : Khối nón có chiều cao \(h = 3cm\) và bán kính đáy \(r = 2cm\) thì có thể tích bằng:
Đáp án: B Phương pháp giải: Thể tích khối nón: \(V = \frac{1}{3}\pi {r^2}h\). Lời giải chi tiết: Thể tích khối nón: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.2^2}.3 = 4\pi \,\left( {c{m^2}} \right)\). Chọn: B
|