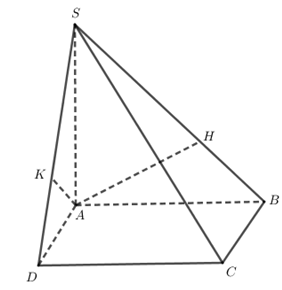
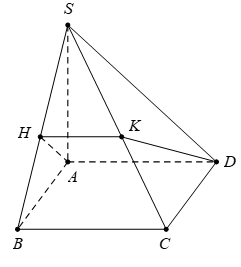
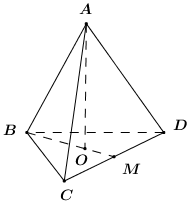
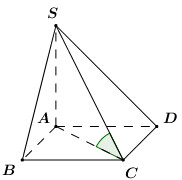
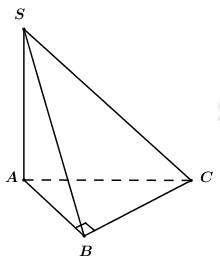
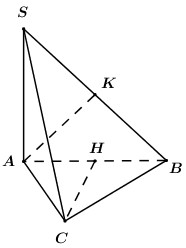
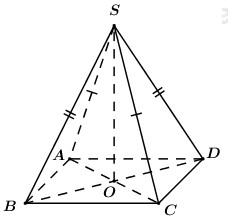
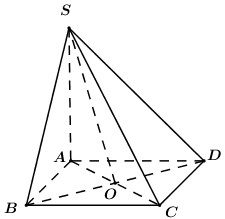
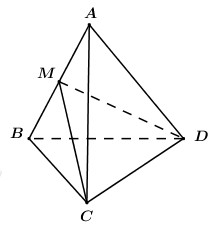
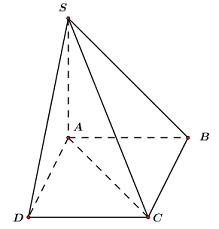
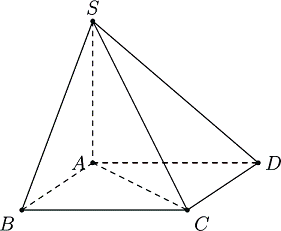
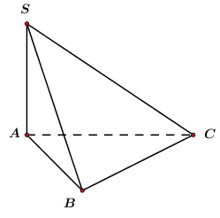
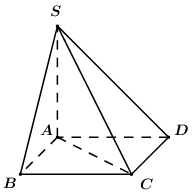
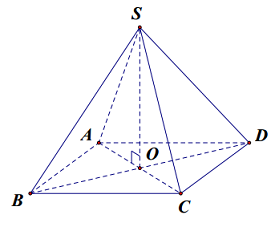
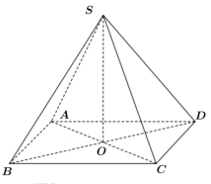
40 bài tập đường thẳng vuông góc với mặt phẳng mức độ thông hiểuLàm bàiCâu hỏi 1 : Hình chóp S.ABCD có đáy là hình vuông, hai mặt bên (SAB) và (SAD) vuông góc với mặt đáy. AH, AK lần lượt là đường cao của tam giác SAB, tam giác SAD. Mệnh đề nào sau đây là sai?
Đáp án: D Phương pháp giải: Sử dụng mối quan hệ vuông góc giữa đường thẳng với đường thẳng, đường thẳng với mặt phẳng. - Hai mặt phẳng cùng vuông góc với đường thẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng đó. - Một đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó. - Một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Lời giải chi tiết: Vì \(\begin{align} & \left\{ \begin{matrix} \left( SAB \right)\bot \left( ABCD \right) \\ \left( SAD \right)\bot \left( ABCD \right) \\ \left( SAB \right)\cap \left( SAD \right)=SA \\\end{matrix} \right.\Rightarrow SA\bot \left( ABCD \right) \\ & \Rightarrow SA\bot BC \\ \end{align}\).\(\left\{ \begin{matrix} SA\bot BC \\ AB\bot BC \\\end{matrix} \right.\Rightarrow BC\bot \left( SAB \right)\Rightarrow BC\bot AH\subset \left( SAB \right)\) Mà \(AH\bot SB\) nên \(AH\bot \left( SBC \right)\Rightarrow AH\bot SC\). Tương tự ta có \(AK\bot \left( SCD \right)\Rightarrow AK\bot SC\) .Do đó \(SC\bot\left( AHK \right)\Rightarrow SC\bot HK\Rightarrow A\)đúng.\(SA\bot \left( ABCD \right)\Rightarrow SA\bot AC\Rightarrow \) B đúng.\(BC\bot AH\) (cmt)\(\Rightarrow C\) đúng. Chọn D
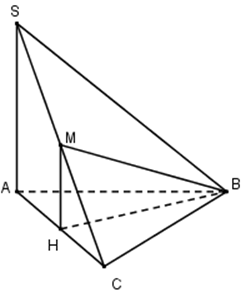
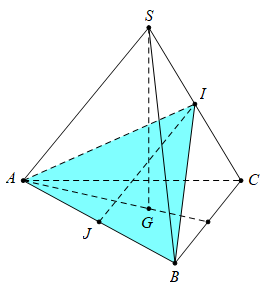
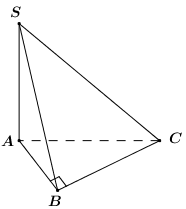
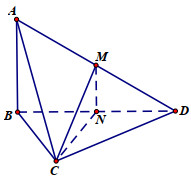
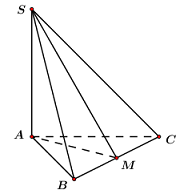
Câu hỏi 2 : Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA vuông góc với mặt phẳng đáy và \(SA=2a\). Gọi M là trung điểm của SC. Tính cosin của góc \(\alpha \) là góc giữa đường thẳng BM và mặt phẳng (ABC).
Đáp án: D Phương pháp giải: Phương pháp: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó Lời giải chi tiết: Cách giải: Gọi H là trung điểm của AC ta có HM // SA nên \(HM\bot \left( ABC \right)\), khi đó \(\left( MB;\left( ABC \right) \right)=\left( MB;HB \right)=\widehat{MBH}\) Ta có : \(SC=\sqrt{4{{a}^{2}}+{{a}^{2}}}=a\sqrt{5}=SB\) Xét tam giác SBC có \(M{{B}^{2}}=\frac{S{{B}^{2}}+B{{C}^{2}}}{2}-\frac{S{{C}^{2}}}{4}=\frac{5{{a}^{2}}+{{a}^{2}}}{2}-\frac{5{{a}^{2}}}{4}=\frac{7{{a}^{2}}}{4}\Leftrightarrow BM=\frac{a\sqrt{7}}{2}\) Tam giác ABC đều cạnh a nên \(BH=\frac{a\sqrt{3}}{2}\) Xét tam giác vuông BHM có: \(\cos \widehat{MBH}=\frac{BH}{BM}=\frac{\frac{a\sqrt{3}}{2}}{\frac{a\sqrt{7}}{2}}=\frac{\sqrt{21}}{7}\) Chọn D. Câu hỏi 3 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB = a,AD = 2a\) , cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng \(\frac{{2{a^3}}}{3}\) . Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD).
Đáp án: C Phương pháp giải: Thể tích khối chóp \(V = \frac{1}{3}{S_d}.h\) : h là chiều cao của khối chóp, S là diện tích đáy. Phương pháp xác định góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng và mặt phẳng chính là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng.
Lời giải chi tiết: Ta có:
\(SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB,AB} \right)} = \widehat {SBA}\) Ta có: \(V = \frac{1}{3}SA.{S_{ABCD}} \Rightarrow SA = \frac{{3V}}{{{S_{ABCD}}}} = \frac{{3.\frac{{2{a^3}}}{3}}}{{a.2a}} = a\) Trong tam giác SAB vuông tại A ta có: \(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = 1 \Rightarrow \widehat {SBA} = {45^0}\)
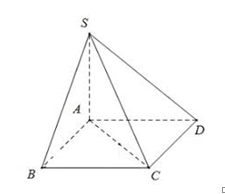
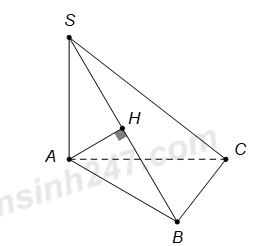
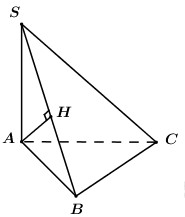
Câu hỏi 4 : Cho hình chóp \(S.ABC\) có \(SA = SB = SC\) và tam giác \(ABC\) vuông tại \(C\). Gọi \(H\) là hình chiếu vuông góc của \(S\) lên \(mp\left( {ABC} \right)\). Khẳng định nào sau đây là khẳng định đúng?
Đáp án: A Phương pháp giải: Gọi \(M\) là trung điểm của \(AB\), chứng minh \(SM \bot \left( {ABC} \right)\) bằng cách sử dụng tính chất của trục đường tròn đáy. Lời giải chi tiết: Gọi \(M\) là trung điểm của \(AB\). Vì \(\Delta ABC\) vuông tại \(C\) nên \(MA = MB = MC\). Mà \(SA = SB = SC\) nên \(SM\) là trục đường tròn ngoại tiếp tam giác \(ABC\). Suy ra \(SM \bot \left( {ABC} \right)\). Vậy \(H \equiv M\) là trung điểm của \(AB\). Câu hỏi 5 : Cho hình chóp S.ABC có đáy ABC vuông tại B, cạnh bên SA vuông góc với đáy. Gọi H là chân đường cao kẻ từ A của tam giác SAB. Khẳng định nào dưới đây là sai ?
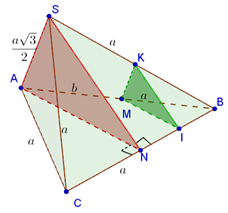
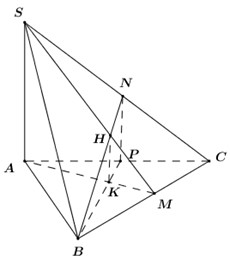
Đáp án: C Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng Lời giải chi tiết: Theo bài ra, ta có \(SA\bot \left( ABC \right)\) mà \(BC\subset \left( ABC \right)\Rightarrow SA\bot BC.\) Tam giác ABC vuông tại B, có \(AB\bot BC\)\(\Rightarrow \)\(BC\bot \left( SAB \right)\Rightarrow BC\bot AH.\) Khi đó \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC.\) Nếu \(AH\bot AC\) mà \(SA\bot AC\) suy ra \(AC\bot \left( SAH \right)\Rightarrow AC\bot AB\) (vô lý). Chọn C Câu hỏi 6 : Cho tứ diện \(SABC\) có hai mặt \(\left( ABC \right)\) và \(\left( SBC \right)\) là hai tam giác đều cạnh \(a,\,\,\,SA=\frac{a\sqrt{3}}{2}.\) Gọi \(M\) là điểm trên \(AB\) sao cho \(AM=b\text{ }\left( 0<b<a \right).\) \(\left( P \right)\) là mặt phẳng qua \(M\)và vuông góc với \(BC.\) Thiết diện của \(\left( P \right)\) và tứ diện \(SABC\) có diện tích bằng ?
Đáp án: C Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, cụ thể là tính diện tích Lời giải chi tiết: Gọi N là trung điểm của BC. Ta có \(\left\{ \begin{array}{l} Theo bài ra \(BC\bot \left( P \right)\Rightarrow \left\{ \begin{align} & M\in \left( P \right) \\ & \left( P \right)//\left( SAN \right) \\\end{align} \right.\). Kẻ \(MI//AN,\,MK//SA\Rightarrow \) Thiết diện của \(\left( P \right)\) và \(S.ABC\) là \(\Delta KMI.\) Mà \(\left\{ \begin{align} & \Delta ABC \\ & \Delta SBC \\\end{align} \right.\) là hai tam giác đều cạnh \(a\Rightarrow AN=SN=\frac{a\sqrt{3}}{2}=SA\Rightarrow \Delta SAN\) là tam giác đều cạnh \(\frac{a\sqrt{3}}{2}\Rightarrow \Delta KMI\) là tam giác đều cạnh \(\frac{\sqrt{3}}{2}.\frac{a-b}{a}\Rightarrow {{S}_{\Delta KMI}}=\frac{3\sqrt{3}}{16}.{{\left( \frac{a-b}{a} \right)}^{2}}.\) Chọn C Câu hỏi 7 : Cho Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều, \(O\) là trung điểm của đường cao \(AH\) của tam giác \(ABC,\text{ }SO\) vuông góc với đáy. Gọi \(I\) là điểm tùy ý trên \(OH\) (không trùng với \(O\) và \(H\)). mặt phẳng \(\left( P \right)\) qua \(I\) và vuông góc với \(OH\). Thiết diện của \(\left( P \right)\) và hình chóp \(S.ABC\) là hình gì?
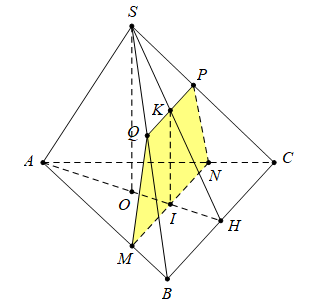
Đáp án: A Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng Lời giải chi tiết: Mặt phẳng (P) vuông góc với OH nên (P) song song với SO. Suy ra (P) cắt (SAH) theo giao tuyến là đường thẳng qua I và song song với SO cắt SH tại K. Từ giả thiết suy ra (P) song song BC, do đó \((P)\) sẽ cắt (ABC), (SBC) lần lượt là các đường thẳng qua I và K song song với BC cắt AB, AC. SB, SC lần lượt tại M, N, P, Q. Do đó thiết diện là tứ giác MNPQ. Ta có MN và PQ cùng song song \(BC\Rightarrow I\) là trung điểm của MN và K là trung điểm của PQ. Mà IK // SO nên \(IK\bot MN,IK\bot PQ\) Do đó MNPQ là hình thang cân. Chọn A Câu hỏi 8 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và \(SA=SB=SC=b\) (\(a>b\sqrt{2}\)). Gọi \(G\) là trọng tâm\(\Delta \,ABC\). Xét mặt phẳng \(\left( P \right)\) đi qua \(A\) và vuông góc với \(SC\) tại điểm I nằm giữa \(S\) và \(C\). Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( P \right)\) là:
Đáp án: A Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, cụ thể là tính diện tích Lời giải chi tiết: Kẻ \(AI\bot SC\), ta dễ dàng chứng minh được \(\Delta SAI=\Delta SBI\,\,\left( c.g.c \right)\Rightarrow \widehat{SIA}=\widehat{SIB}={{90}^{0}}\Rightarrow BI\bot SC\) \(\Rightarrow SC\bot \left( ABI \right)\). Thiết diện là tam giác AIB. Ta có \(AI = AC\sin \widehat {ACS} = a.\sqrt {1 - {{\cos }^2}\widehat {ACS}} = a.\sqrt {1 - {{\left( {\dfrac{{{a^2} + {b^2} - {b^2}}}{{2ab}}} \right)}^2}} = a\sqrt {1 - {{\left( {\frac{a}{{2b}}} \right)}^2}} .\) Gọi J là trung điểm của AB. Dễ thấy tam giác AIB cân tại I, suy ra \(IJ\bot AB\) \(\begin{array}{l} Do đó: \(S = \dfrac{1}{2}AB.IJ = \dfrac{{{a^2}\sqrt {{a^2} + 3{b^2} - 4ab} }}{{4b}}\) Chọn A Câu hỏi 9 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a.\) Cạnh bên \(SA\) vuông góc với \(mp\,\,\left( ABCD \right),\,\,SA=a\sqrt{2}.\) Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(A\) và vuông góc với \(SB.\) Mặt phẳng \(\left( \alpha \right)\) cắt hình chóp theo một thiết diện có diện tích \(S.\) Tính \(S\) theo \(a.\)
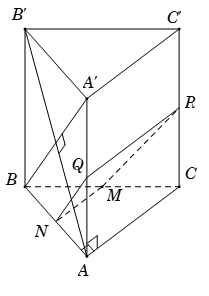
Đáp án: B Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác Lời giải chi tiết: Ta có AD vuông góc với SA và AB\(\Rightarrow AD\bot mp\,\,\left( SAB \right)\Rightarrow AD\bot SB.\) Vẽ đường cao AH trong tam giác SAB Lại có AD và AH qua A và vuông góc với SB. Vậy mặt phẳng \(\left( \alpha \right)\) chính là mặt phẳng (AHD) Mặt khác AD // mp(SBC) mà \(AD\subset mp\,\,\left( AHD \right)\) Vậy mặt phẳng (SBC) cắt mặt phẳng (AHD) theo giao tuyến HK // AD. Do đó mặt cắt là hình thang ADKH mà \(AD\bot mp\,\,\left( SAB \right)\)\(\Rightarrow \,AD\bot AH.\) Suy ra tứ giác ADKH là hình thang vuông. Tam giác SAB vuông \(\Rightarrow \,\,AH=\frac{SA.AB}{SC}=\frac{a\sqrt{2}.a}{a\sqrt{3}}=\frac{a\sqrt{6}}{3}.\) Và \(S{{A}^{2}}=SH.HB\,\,\Rightarrow \,\,SH=\frac{S{{A}^{2}}}{SB}=\frac{2{{a}^{2}}}{a\sqrt{3}}=\frac{2a\sqrt{3}}{3}.\) Ta có \(HK\)//\(BC\)\(\Rightarrow \,\,\frac{HK}{BC}=\frac{SH}{SB}\,\,\Rightarrow \,\,HK=\frac{SH.BC}{SB}=\frac{\frac{2a\sqrt{3}}{3}.a}{a\sqrt{3}}=\frac{2a}{3}.\) Do đó \({{S}_{ADKH}}=\frac{AH}{2}.\left( HK+AD \right)=\frac{a\sqrt{6}}{6}.\left( \frac{2a}{3}+a \right)=\frac{a\sqrt{6}}{6}.\frac{5a}{3}=\frac{5{{a}^{2}}\sqrt{6}}{18}.\) Chọn B Câu hỏi 10 : Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) với \(BC=a\sqrt{2}\); \(AA'=a\) và vuông góc với đáy. Mặt phẳng \(\left( \alpha \right)\) qua \(M\) là trung điểm của \(BC\) và vuông góc với \(AB'\). Thiết diện tạo bởi \(\left( \alpha \right)\) với hình lăng trụ \(ABC.A'B'C'\) là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Gọi N là trung điểm \(AB\Rightarrow MN//AC\Rightarrow MN\bot AB\). Ta có \(\left\{ \begin{align} & MN\bot AB \\ & MN\bot AA' \\\end{align} \right.\Rightarrow MN\bot \left( ABB'A' \right)\Rightarrow MN\bot AB'\Rightarrow MN\subset \left( \alpha \right).\) Từ giả thiết \(\Rightarrow \)\(AB=a=AA'\Rightarrow ABB'A'\) là hình vuông \(\Rightarrow BA'\bot AB'\) Trong mp \(\left( ABB'A' \right)\) kẻ \(NQ\parallel BA'\) với \(Q\in AA'\). Trong mp \(\left( ACC'A' \right)\) kẻ \(QR\parallel AC\) với \(R\in CC'\). Vậy thiết diện là hình thang MNPQ vuông (do MN và QR cùng song song với AC và \(MN\bot NQ\)). Chọn B. Câu hỏi 11 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB=a,\) \(BC=2a.\) Tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng \(\left( \alpha \right)\) đi qua \(S\) vuông góc với \(AB.\) Tính diện tích \(S\) của thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp đã cho.
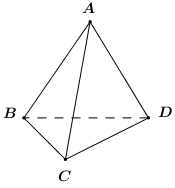
Đáp án: B Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác Lời giải chi tiết: Gọi H là trung điểm \(AB\Rightarrow SH\bot AB.\) Suy ra: \(\bullet \) \(SH\subset \left( \alpha \right)\). \(\bullet \) \(SH\bot \left( ABCD \right)\) (do \(\left( SAB \right)\bot \left( ABCD \right)\) theo giao tuyến \(AB\)). Kẻ \(HM\bot AB\text{ }\left( M\in CD \right)\Rightarrow HM\subset \left( \alpha \right).\) Do đó thiết diện là tam giác SHM vuông tại H. Ta có \(SH=\frac{a\sqrt{3}}{2}\), \(HM=BC=2a.\) Vậy \({{S}_{\Delta SHM}}=\frac{1}{2}.\frac{a\sqrt{3}}{2}.2a=\frac{{{a}^{2}}\sqrt{3}}{2}.\) Chọn B Câu hỏi 12 : Cho tứ diện ABCD đều. Gọi \(\alpha \) là góc giữa AB và mặt phẳng (BCD). Chọn khẳng định đúng trong các khẳng định sau ?
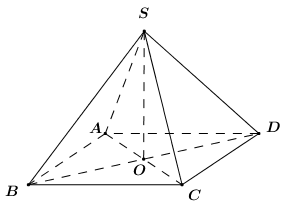
Đáp án: A Phương pháp giải: Áp dụng phương pháp tìm góc giữa đường thẳng và mặt phẳng – hệ thức lượng trong tam giác vuông để giải quyết yêu cầu của bài toán Lời giải chi tiết: Gọi H là trọng tâm tam giác đều \(BCD \Rightarrow AH \bot \left( {BCD} \right).\) Gọi a là độ dài cạnh của tứ diện \(ABCD \Rightarrow BH = \frac{2}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}.\) Khi đó \(\alpha = \widehat {ABH} \Rightarrow \cos \alpha = \frac{{BH}}{{AB}} = \frac{{\sqrt 3 }}{3}.\) Chọn A. Câu hỏi 13 : Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(2a\), góc \(\angle ADC = {60^0}\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(SO \bot \left( {ABCD} \right)\) và \(SO = 3a\). Góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( {ABCD} \right)\) bằng:
Đáp án: A Phương pháp giải: - Góc giữa \(SD\) và mặt phẳng \(\left( {ABCD} \right)\) là góc giữa \(SD\) và hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\). - Sử dụng công thức tính nhanh: Đường cao của tam giác đều cạnh \(a\) là \(\dfrac{{a\sqrt 3 }}{2}\). - Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết: Ta có: \(SO \bot \left( {ABCD} \right)\) nên \(OD\) là hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right) = \angle \left( {SD;OD} \right) = \angle SDO\). Xét \(\Delta ACD\) có: \(AD = CD = 2a,\,\,\angle ADC = {60^0}\) \( \Rightarrow \Delta ACD\) đều cạnh \(2a\). Mà \(O = AC \cap BD \Rightarrow O\) là trung điểm của \(AC\) \( \Rightarrow DO = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \). Xét \(\Delta SDO\) có \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OD \Rightarrow \Delta SDO\) vuông tại \(O\) \( \Rightarrow \tan \angle SDO = \dfrac{{SO}}{{OD}} = \dfrac{{3a}}{{a\sqrt 3 }} = \sqrt 3 \). Vậy \(\angle SDO = {60^0}\). Chọn A. Câu hỏi 14 : Cho tứ diện đều \(ABCD\). Cosin góc giữa \(AB\) và \(mp\left( {BCD} \right)\) bằng:
Đáp án: B Phương pháp giải: - Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy. - Góc giữa đường và mặt là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(CD\), \(O\) là tâm đường tròn ngoại tiếp tam giác đều \(BCD\) \( \Rightarrow AO \bot \left( {BCD} \right)\). Khi đó \(OB\) là hình chiếu vuông góc của \(AB\) lên \(\left( {BCD} \right)\) \( \Rightarrow \angle \left( {AB;\left( {BCD} \right)} \right) = \angle \left( {AB;OB} \right) = \angle ABO\). Tam giác \(BCD\) đều cạnh \(a\) nên \(BM = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow BO = \dfrac{2}{3}BM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\). Ta có \(AO \bot \left( {BCD} \right)\) nên \(AO \bot OB\), suy ra \(\Delta ABO\) vuông tại \(O\). \( \Rightarrow \cos \angle ABO = \dfrac{{OB}}{{AB}} = \dfrac{{\dfrac{{a\sqrt 3 }}{3}}}{a} = \dfrac{{\sqrt 3 }}{3}\). Vậy \(\cos \angle \left( {AB;\left( {BCD} \right)} \right) = \dfrac{{\sqrt 3 }}{3}\). Chọn B. Câu hỏi 15 : Cho hình chóp \(S.ABC\) có cạnh bên \(SA\) vuông góc với đáy, tam giác \(ABC\) vuông tại \(B\). Khẳng định nào sau đây đủng?
Đáp án: B Phương pháp giải: Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Lời giải chi tiết:
Cách giải: Ta có: \(SA \bot \left( {ABC} \right)\) nên \(SA \bot BC\). \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\). Vậy khẳng định B đúng. Chọn B. Câu hỏi 16 : Trong không gian cho đường thẳng \(\Delta \) không nằm trong mặt phẳng \(\left( P \right)\). Đường thẳng \(\Delta \) vuông góc với mặt phẳng \(\left( P \right)\) nếu:
Đáp án: C Phương pháp giải: Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Lời giải chi tiết: Trong không gian cho đường thẳng \(\Delta \) không nằm trong mặt phẳng \(\left( P \right)\). Đường thẳng \(\Delta \) vuông góc với mặt phẳng \(\left( P \right)\) nếu: \(\Delta \) vuông góc với mọi đường thẳng nằm trong mặt phẳng \(\left( P \right)\). Chọn C. Câu hỏi 17 : Hai mặt phẳng vuông góc với nhau khi và chỉ khi:
Đáp án: C Phương pháp giải: Sử dụng định lí: Hai mặt phẳng vuông góc với nhau khi và chỉ khi: Mặt phẳng này chứa đường thẳng vuông góc với mặt phẳng kia. Lời giải chi tiết: Hai mặt phẳng vuông góc với nhau khi và chỉ khi mặt phẳng này chứa đường thẳng vuông góc với mặt phẳng kia. Chọn C. Câu hỏi 18 : Trong không gian cho đường thẳng \(\Delta \) và điểm \(A\). Có bao nhiêu mặt phẳng đi qua \(A\) và vuông góc với đường thẳng \(\Delta \) đã cho?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Trong không gian cho đường thẳng \(\Delta \) và điểm \(A\). Có duy nhất mặt phẳng đi qua \(A\) và vuông góc với đường thẳng \(\Delta \) đã cho. Chọn D. Câu hỏi 19 : Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thoi tâm \(O\) và \(SA = SC\), \(SB = SD\). Trong các khẳng định sau, khẳng định nào sai?
Đáp án: C Phương pháp giải: Sử dụng định lí \(d \bot \left( P \right) \Rightarrow d \bot a\,\,\,\forall a \subset \left( P \right)\). Lời giải chi tiết:
Vì \(ABCD\) là hình thoi nên \(AC \bot BD\) và \(O\) là trung điểm của \(AC,\,\,BD\). \( \Rightarrow \) Đáp án D đúng. Vì \(SB = SD \Rightarrow \Delta SBD\) cân tại \(S\), do đó \(SO \bot BD\) (trung tuyến đồng thời là đường cao). Ta có: \(\left\{ \begin{array}{l}BD \bot SO\\BD \bot AC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\). Mà \(SA,\,\,AC \subset \left( {SAC} \right)\) nên \(BD \bot SA,\,\,BD \bot SC\), suy ra các đáp án A, B đúng. Vậy khẳng định C sai. Chọn C. Câu hỏi 20 : Cho hình chóp S.ABC có \(SA \bot \left( {SBC} \right)\). Gọi H, K lần lượt là trực tâm các tam giác SBC và ABC. Mệnh đề nào sai trong các mệnh đề sau?
Đáp án: C Phương pháp giải: Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Lời giải chi tiết:
Gọi \(M\) là giao điểm của \(AK\) và \(BC\), ta có \(AM \bot BC\). \(\left\{ \begin{array}{l}BC \bot AM\\BC \bot SA\,\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right)\). \( \Rightarrow BC \bot SM \Rightarrow SM\) là đường cao của \(\Delta SBC\), do đó \(K \in SM\). Suy ra SH, AK và BC đồng quy tại M nên đáp án D đúng. Mà \(BC \bot \left( {SAM} \right)\,\,\left( {cmt} \right),\,\,\left( {SAM} \right) \equiv \left( {SAH} \right)\) nên \(BC \bot \left( {SAH} \right)\), suy ra đáp án A đúng. Trong \(\left( {ABC} \right)\) kéo dài BK cắt AC tại P, trong (SBC) kéo dài BH cắt SC tại N. Ta có: \(\left\{ \begin{array}{l}BP \bot AC\\BP \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BP \bot \left( {SAC} \right)\) \( \Rightarrow BP \bot SC\). Suy ra \(\left\{ \begin{array}{l}SC \bot BP\\SC \bot BN\end{array} \right. \Rightarrow SC \bot \left( {BPN} \right)\), mà \(HK \subset \left( {BPN} \right) \Rightarrow HK \bot SC\). Mặt khác \(HK \subset \left( {SAM} \right) \Rightarrow HK \bot BC\). Nên \(HK \bot \left( {SBC} \right)\), do đó đáp án B đúng. Chọn C. Câu hỏi 21 : Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình vuông cạnh bằng \(a\) và \(SA \bot \left( {ABCD} \right).\) Biết \(SA = \dfrac{{a\sqrt 6 }}{3}\). Tính góc giữa \(SC\) và \(\left( {ABCD} \right).\)
Đáp án: C Phương pháp giải: - Góc giữa SC và mặt phẳng (ABCD) là góc giữa SC và hình chiếu của SC lên (ABCD). - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết:
Vì \(SA \bot \left( {ABCD} \right)\) nên AC là hình chiếu của SC lên (ABCD). \( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA\). Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AC\), do đó tam giác SAC vuông tại A. Ta có: ABCD là hình vuông cạnh a nên \(AC = a\sqrt 2 \). Xét tam giác vuông SAC có: \(\tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt 6 }}{3}:a\sqrt 2 = \dfrac{{\sqrt 3 }}{3}\)\( \Rightarrow \angle SCA = {30^0}\) Vậy góc giữa SC và (ABCD) bằng \({30^0}\). \(MN = \sqrt {M{P^2} + N{P^2}} = \sqrt {\dfrac{{9{a^2}}}{4} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {10} }}{2}\). Chọn C. Câu hỏi 22 : Cho tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với mặt phẳng (BCD), AB = 2a. M là trung điểm của đoạn AD, gọi \(\varphi \) là góc giữa CM và mặt phẳng BCD. Khi đó:
Đáp án: B Phương pháp giải: - Gọi N là trung điểm của BD. Chứng minh \(MN \bot \left( {BCD} \right)\). - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết:
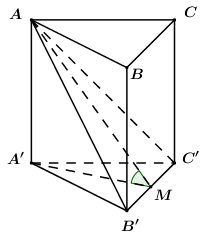
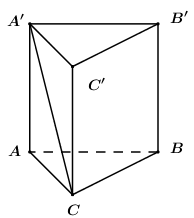
Gọi N là trung điểm của BD, ta có MN là đường trung bình của tam giác ABD nên MN // AB và \(MN = \dfrac{1}{2}AB = a.\) Mà \(AB \bot \left( {BCD} \right)\,\,\left( {gt} \right)\) nên \(MN \bot \left( {BCD} \right)\), do đó CN là hình chiếu của CM lên (BCD) \( \Rightarrow \angle \left( {CM;\left( {BCD} \right)} \right) = \angle \left( {CM;CN} \right) = \angle MCN = \varphi \). Vì tam giác BCD đều cạnh a nên \(CN = \dfrac{{a\sqrt 3 }}{2}\). Ta có: \(MN \bot \left( {BCD} \right) \Rightarrow MN \bot CN\) \( \Rightarrow \Delta CMN\) vuông tại N. Vậy \(\tan \varphi = \tan \angle MCN = \dfrac{{MN}}{{CN}} = a:\dfrac{{a\sqrt 3 }}{2} = \dfrac{{2\sqrt 3 }}{3}\). Chọn B. Câu hỏi 23 : Cho hình lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng 2a, cạnh bên bằng a. Tính góc giữa hai mặt pẳng (AB’C’) và (A’B’C’)?
Đáp án: A Phương pháp giải: - Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết:
Gọi M là trung điểm của B'C', do tam giác A'B'C' đều nên \(A'M \bot B'C'\). Câu hỏi 24 : Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\) và \(\Delta ABC\) vuông ở B, AH là đường cao của \(\Delta SAB\). Khẳng định nào sau đây là sai?
Đáp án: C Phương pháp giải: - Chứng minh \(BC \bot \left( {SAB} \right)\), từ đó chứng minh \(BC \bot AH\). - Chứng minh \(AH \bot \left( {SBC} \right)\). - Sử dụng định lí: \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)\), \(\left\{ \begin{array}{l}a \bot \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow a \bot d\). Lời giải chi tiết: + \(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\,\,\left( {gt} \right)\\BC \subset \left( {ABC} \right)\end{array} \right. \Rightarrow SA \bot BC\), suy ra đáp án A đúng. + \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {do\,\,SA \bot \left( {ABC} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\) \( \Rightarrow BC \bot AH\). + \(\left\{ \begin{array}{l}AH \bot BC\\AH \bot SB\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\). Mà \(BC,\,\,SC \subset \left( {SBC} \right)\) nên \(AH \bot BC,\,\,AH \bot SC\), do đó đáp án B, D đúng. Chọn C. Câu hỏi 25 : Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và \(AB \bot BC\). Số mặt của tứ diện S.ABC là tam giác vuông là:
Đáp án: D Phương pháp giải: Sử dụng các định lí: \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)\), \(\left\{ \begin{array}{l}a \bot \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow a \bot d\). Lời giải chi tiết:
+ Ta có \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB,\,\,SA \bot AC\) \( \Rightarrow \Delta SAB,\,\,\Delta SAC\) là các tam giác vuông tại A. + \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\) \( \Rightarrow BC \bot SB\) \( \Rightarrow \Delta SBC\) vuông tại B. + \(\Delta ABC\) vuông tại B (gt). Vậy tứ diện S.ABC có cả 4 mặt là tam giác vuông. Chọn D.
Câu hỏi 26 : Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và đáy ABC là tam giác cân ở C. Gọi H, K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây sai?
Đáp án: D Phương pháp giải: Sử dụng các định lí: \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap b \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)\), \(\left\{ \begin{array}{l}a \bot \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow a \bot d\). Lời giải chi tiết:
+ \(\left\{ \begin{array}{l}CH \bot AB\\CH \bot SA\end{array} \right. \Rightarrow CH \bot \left( {SAB} \right)\). + \(\left\{ \begin{array}{l}CH \bot \left( {SAB} \right)\\SA,\,\,SB,\,\,AK \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}CH \bot SA\\CH \bot SB\\CH \bot AK\end{array} \right.\) Vậy các khẳng định A, B, C đúng. Chọn D. Câu hỏi 27 : Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA = SC, SB = SD. Trong các khẳng định sau khẳng định nào đúng?
Đáp án: B Phương pháp giải: Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Lời giải chi tiết:
Vì ABCD là hình bình hành tâm O nên O là trung điểm của AC và BD. Xét \(\Delta SAC\) có SA = SC \( \Rightarrow \Delta SAC\) cân tại S \(SO \bot AC\) (đương trung tuyến đồng thời là đường cao). Chứng minh tương tự ta có \(SO \bot BD\). \( \Rightarrow SO \bot \left( {ABCD} \right)\). Chọn B. Câu hỏi 28 : Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy (ABCD). Khẳng định nào sau đây sai?
Đáp án: A Phương pháp giải: Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Lời giải chi tiết:
+ Vì \(SA \bot \left( {ABCD} \right)\,\,\left( {gt} \right)\), \(\left( {ABC} \right) \equiv \left( {ABCD} \right)\) nên \(SA \bot \left( {ABC} \right)\), suy ra khẳng định B đúng. + \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\), suy ra khẳng định C đúng. + \(\left\{ \begin{array}{l}BD \bot AC\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAC} \right)\), suy ra khẳng định D đúng. Chọn A. Câu hỏi 29 : Cho tứ diện ABCD có hai mặt ABC và ABD là hai tam giác đều. Gọi M là trung điểm của AB. Khẳng định nào sau đây đúng?
Đáp án: B Phương pháp giải: - Sử dụng tính chất của tam giác đều: Trong tam giác đều, đường trung tuyến đồng thời là đường cao. - Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Lời giải chi tiết:
+ \(\Delta ABC\) đều \( \Rightarrow CM \bot AB\) (đường trung tuyến đồng thời là đường cao) + \(\Delta ABD\) đều \( \Rightarrow DM \bot AB\) (đường trung tuyến đồng thời là đường cao) + \(\left\{ \begin{array}{l}AB \bot CM\\AB \bot DM\end{array} \right. \Rightarrow AB \bot \left( {MCD} \right)\). Chọn B. Câu hỏi 30 : Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B. Vẽ \(SH \bot \left( {ABC} \right)\) \(\left( {H \in \left( {ABC} \right)} \right)\). Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: - Hình chóp có các cạnh bên bằng nhau có hình chiếu vuông góc của đỉnh trùng với tâm đường tròn ngoại tiếp đáy. - Tam giác vuông có tâm đường tròn ngoại tiếp trùng với trung điểm của cạnh huyền. Lời giải chi tiết:
+ Do SA = SB = SC, \(SH \bot \left( {ABC} \right)\) nên H là tâm đường tròn ngoại tiếp \(\Delta ABC\). + \(\Delta ABC\) vuông tại B nên tâm đường tròn ngoại tiếp tam giác là trung điểm của cạnh huyền AC. Vậy H là trung điểm của AC. Chọn C. Câu hỏi 31 : Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình vuông cạnh \(3a,\,\,SA = \sqrt 6 a\) và \(SA = \sqrt 6 a\) và \(SA\) vuông góc với \(\left( {ABCD} \right).\) Góc giữa \(SC\) và \(\left( {ABCD} \right)\) là:
Đáp án: B Phương pháp giải: Góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(a\) và hình chiếu \(a'\) của \(a\) trên \(\left( P \right).\) Lời giải chi tiết:
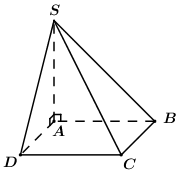
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow AC\) là hình chiếu của \(SC\) trên \(\left( {ABCD} \right).\) \( \Rightarrow \angle \left( {SC;\,\,\left( {ABCD} \right)} \right) = \angle \left( {SC,\,\,AC} \right) = \angle SCA.\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(B\) ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {3a} \right)}^2}} = 3a\sqrt 2 .\) Xét \(\Delta SAC\) vuông tại \(A\) ta có: \(\begin{array}{l}\tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt 6 }}{{3a\sqrt 2 }} = \dfrac{{\sqrt 3 }}{3}\\ \Rightarrow \angle SCA = {30^0}.\end{array}\) Chọn B. Câu hỏi 32 : Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, \(SA = a\sqrt 3 \), tứ giác ABCD là hình vuông, \(BD = a\sqrt 2 \)( minh họa như hình bên). Góc giữa đường thẳng SB và mặt phẳng \(\left( {SAD} \right)\)bằng
Đáp án: B Phương pháp giải: - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết:
Ta có SB và mặt phẳng \(\left( {SAD} \right)\) cắt nhau tại S. Mặt khác \(SA \bot \left( {ABCD} \right) \Rightarrow BA \bot SA\) và ABCD là hình vuông \( \Rightarrow BA \bot AD\) Khi đó \(BA \bot \left( {SAD} \right) \Rightarrow A\) là hình chiếu của B trên mặt phẳng \(\left( {SAD} \right)\). Suy ra góc giữa đường thẳng SB và mặt phẳng \(\left( {SAD} \right)\) là góc giữa SB và SA là \(\angle BSA\). Vì \(ABCD\) là hình vuông có \(BD = a\sqrt 2 \Rightarrow AB = a\). Xét tam giác SAB vuông tại A \( \Rightarrow \tan \angle BSA = \dfrac{{AB}}{{SA}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }} \Rightarrow \angle BSA = 30^\circ .\) Vậy \(\angle \left( {SB;\left( {SAD} \right)} \right) = {30^0}\). Chọn B. Câu hỏi 33 : Cho hình chóp tam giác \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = a\sqrt 3 \). Tam giác \(ABC\) đều, cạnh \(a\). Góc giữa \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng:
Đáp án: B Phương pháp giải: Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và đường thẳng a’ là hình chiếu của a trên (P). Lời giải chi tiết:
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow AC\) là hình chiếu của \(SC\) trên \(\left( {ABC} \right).\) \( \Rightarrow \angle \left( {SC,\,\,\left( {ABC} \right)} \right) = \angle \left( {SC,\,\,AC} \right) = \angle SCA\) Xét \(\Delta SAC\) vuông tại \(A\) ta có: \(\begin{array}{l}\tan \angle SCA = \frac{{SA}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \\ \Rightarrow \angle SCA = {60^0}.\end{array}\) Chọn B. Câu hỏi 34 : Cho hình chóp \(SABC\) có đáy là tam giác \(ABC\) vuông cân tại \(A,\)\(SA\) vuông góc với mặt phẳng đáy, \(SA = \dfrac{{a\sqrt 6 }}{2},\,\,AB = a.\) Gọi \(M\) là trung điểm của \(BC.\) Góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABC} \right)\) có số đo bằng:
Đáp án: C Phương pháp giải: Góc giữa \(SM\) và \(\left( {ABC} \right)\) là góc giữa \(SM\) và hình chiếu của \(SM\) trên \(\left( {ABC} \right).\) Lời giải chi tiết:
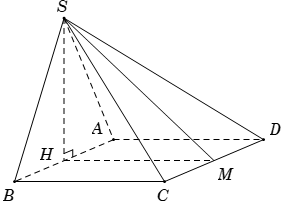
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow AM\) là hình chiếu của \(SM\) trên \(\left( {ABC} \right).\) \( \Rightarrow \angle \left( {SM,\,\,\left( {ABC} \right)} \right) = \angle \left( {SM,\,\,AM} \right) = \angle SMA.\) Áp dụng định lý Pi-ta-go cho \(\Delta ABC\) vuông cân tại \(A\) có \(AB = a\) ta có: \(BC = \sqrt {A{B^2} + A{C^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) \(AM\) là đường trung tuyến của \(\Delta ABC\) \( \Rightarrow AM = \dfrac{{BC}}{2} = \dfrac{{a\sqrt 2 }}{2}.\) Xét \(\Delta SAM\) vuông tại \(A\) ta có: \(\tan \angle SMA = \dfrac{{SA}}{{AM}} = \dfrac{{a\sqrt 6 }}{2}:\dfrac{{a\sqrt 2 }}{2} = \sqrt 3 \) \( \Rightarrow \angle SMA = {60^0}.\) Chọn C. Câu hỏi 35 : Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật có cạnh \(AB = a,\)\(BC = 2a\). Hai mặt bên \(\left( {SAB} \right)\)và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng đáy \(\left( {ABCD} \right)\), cạnh \(SA = a\sqrt {15} \). Tính góc tạo bởi đường thẳng SC và mặt phẳng \(\left( {ABD} \right)\).
Đáp án: A Phương pháp giải: - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng lên mặt phẳng đó. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAD} \right) = SA\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\end{array} \right. \Rightarrow SA \bot \left( {ABCD} \right) \Rightarrow SA \bot \left( {ABD} \right)\). \( \Rightarrow AC\) là hình chiếu của \(SC\) lên \(\left( {ABD} \right)\). \( \Rightarrow \angle \left( {SC;\left( {ABD} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA\). Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \). Xét tam giác vuông \(SAC\): \(\tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt {15} }}{{a\sqrt 5 }} = \sqrt 3 \Rightarrow \angle SCA = {60^0}.\) Vậy \(\angle \left( {SC;\left( {ABD} \right)} \right) = {60^0}\). Chọn A. Câu hỏi 36 : Cho hình lăng trụ đều \(ABC.A'B'C'\) có \(AB = a\), \(AA' = a\sqrt 3 \). Góc giữa đường thẳng \(AC'\) và mặt phẳng \(\left( {ABC} \right)\) bằng:
Đáp án: D Phương pháp giải: - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết:
Ta có: \(AA' \bot \left( {ABC} \right)\) nên \(AC\) là hình chiếu của \(A'C\) lên \(\left( {ABC} \right)\). \( \Rightarrow \angle \left( {A'C;\left( {ABC} \right)} \right) = \angle \left( {A'C;AC} \right) = \angle A'CA\). Xét tam giác vuông \(A'AC\) có: \(\tan \angle A'CA = \dfrac{{AA'}}{{AC}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 \). \( \Rightarrow \angle A'CA = {60^0}\). Vậy \(\angle \left( {A'C;\left( {ABC} \right)} \right) = {60^0}\). Chọn D. Câu hỏi 37 : Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(a\), \(SA\) vuông góc với mặt phẳng đáy, \(SA = a\sqrt 3 \) (minh họa như hình vẽ bên dưới).
Góc giữa \(SD\) và mặt phẳng \(\left( {ABCD} \right)\) bằng:
Đáp án: C Phương pháp giải: - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết: Vì \(SA \bot \left( {ABCD} \right)\) nên \(AD\) là hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right) = \angle \left( {SD;AD} \right) = \angle SDA\). Xét tam giác vuông \(SAD\) có: \(\tan \angle SDA = \dfrac{{SA}}{{AD}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 \) \( \Rightarrow \angle SDA = {60^0}\). Vậy \(\angle \left( {SD;\left( {ABCD} \right)} \right) = {60^0}\). Chọn C. Câu hỏi 38 : Cho hình chóp tứ giác đều \(SABCD,\)\(AB = a\sqrt 2 ,\,\,SA = 2a.\) Góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) bằng:
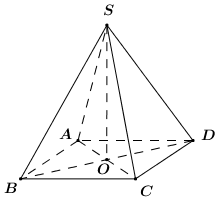
Đáp án: C Phương pháp giải: Góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) góc giữa \(SA\) và hình chiếu vuông góc của \(SA\) trên \(\left( {ABCD} \right).\) Lời giải chi tiết:
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\) Ta có \(SABCD\) là hình chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right).\) \( \Rightarrow OA\) là hình chiếu vuông góc của \(SA\) trên \(\left( {ABCD} \right)\) \( \Rightarrow \angle \left( {SA,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SA,\,\,OA} \right) = \angle SAO\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(B\) ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = 2a\) \( \Rightarrow AO = \dfrac{1}{2}AC = a.\) Xét \(\Delta SAO\) vuông tại \(O\) ta có: \(\cos \angle SAO = \dfrac{{OA}}{{SA}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\) \( \Rightarrow \angle SAO = {60^0}.\) Chọn C. Câu hỏi 39 : Cho hình chóp đều \(S.ABCD\) có \(AB = 2a,\,\,SA = 2a\sqrt 2 .\) Góc giữa \(SB\) và mặt phẳng \(\left( {ABCD} \right)\) bằng:
Đáp án: C Phương pháp giải: Góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABCD} \right)\) là góc giữa \(SB\) và hình chiếu vuông góc của \(SB\) trên \(\left( {ABCD} \right).\) Lời giải chi tiết:
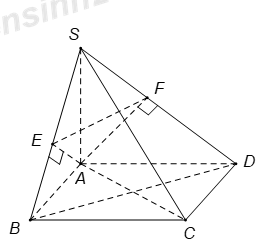
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\) \( \Rightarrow SO \bot \left( {ABCD} \right).\) \( \Rightarrow OB\) là hình chiếu vuông góc của \(SB\) trên \(\left( {ABCD} \right).\) \( \Rightarrow \angle \left( {SB,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SB,\,\,OB} \right) = \angle SBO\) Áp dụng định lý Pitago cho \(\Delta ABD\) vuông tại \(A\) ta có: \(\begin{array}{l}BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {4{a^2} + 4{a^2}} = 2a\sqrt 2 \\ \Rightarrow OB = \dfrac{1}{2}BD = a\sqrt 2 .\end{array}\) Xét \(\Delta SBO\) vuông tại \(O\) ta có: \(\cos SBO = \dfrac{{BO}}{{SB}} = \dfrac{{a\sqrt 2 }}{{2a\sqrt 2 }} = \dfrac{1}{2}\)\( \Rightarrow \angle SBO = {60^0}.\) Vậy \(\angle \left( {SB;\,\,\left( {ABCD} \right)} \right) = {60^0}.\) Chọn C. Câu hỏi 40 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi AE, AF lần lượt là đường cao của tam giác SAB và tam giác SAD. Khẳng định nào dưới đây là đúng ?
Đáp án: D Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng Lời giải chi tiết:
Vì SA vuông góc với mặt phẳng (ABCD)\(\Rightarrow \)\(SA\bot BC.\) Mà \(AB\bot BC\) nên suy ra \(BC\bot \left( SAB \right)\Rightarrow BC\bot AE\subset \left( SAB \right).\) Tam giác SAB có đường cao AE\(\Rightarrow \,\,AE\bot SB\) Mà \(AE\bot BC\Rightarrow AE\bot \left( SBC \right)\Rightarrow AE\bot SC.\) Tương tự, ta chứng minh được \(AF\bot SC\). Do đó \(SC\bot \left( AEF \right).\) Chọn D
|