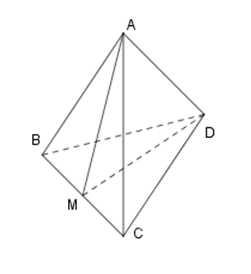
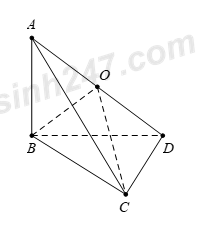
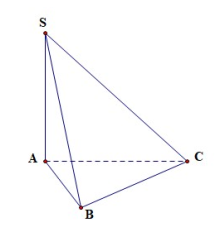
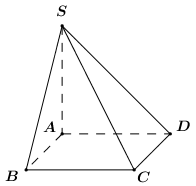
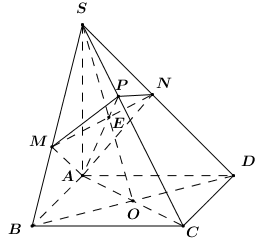
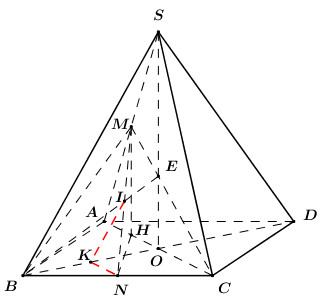
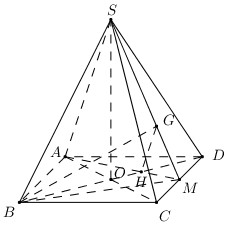
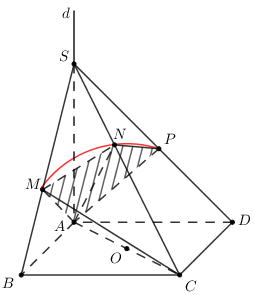
30 bài tập đường thẳng vuông góc với mặt phẳng mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho tứ diện \(ABCD\) có \(AB=AC=2,\,DB=DC=3.\) Khẳng định nào sau đây đúng?
Đáp án: A Phương pháp giải: Phương pháp. Gọi \(M\) là trung điểm của \(BC.\) Chứng minh\(BC\bot \left( AMD \right)\Rightarrow BC\bot AD.\) Lời giải chi tiết: Lời giải chi tiết. Gọi \(M\) là trung điểm của \(BC.\) Khi đó do \(\Delta ABC\) cân tại \(A\,\,\left( AB=AC \right)\) Nên \(AM\bot BC\,\,\left( 1 \right).\) Tương tự \(DM\bot BC\,\,\left( 2 \right)\) do tam giác \(\Delta BCD\) có \(BD=CD.\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(BC\bot \left( AMD \right)\Rightarrow BC\bot AD.\) Chọn đáp án A. Câu hỏi 2 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy và AB = a, \(AD = a\sqrt 2 ,SA = a\sqrt 3 \). Số đo của góc giữa SC và mặt phẳng (ABCD) là:
Đáp án: B Phương pháp giải: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. Lời giải chi tiết:
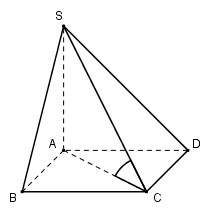
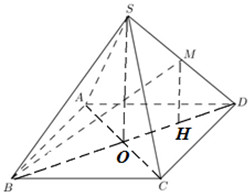
Do \(SA \bot \left( {ABCD} \right) \Rightarrow \) A là hình chiếu của S trên (ABCD) nên AC là hình chiếu của SC trên (ABCD). \( \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}\). Xét tam giác vuông ABC có \(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 3 \), Xét tam giác vuông SAC có \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 3 }}{{a\sqrt 3 }} = 1 \Rightarrow \widehat {SCA} = {45^0}\) Chọn B. Câu hỏi 3 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi O là tâm đường tròn ngoại tiếp tam giác SBC, H là hình chiếu của O trên (ABC). Khẳng định nào sau đây là đúng ?
Đáp án: C Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng Lời giải chi tiết:
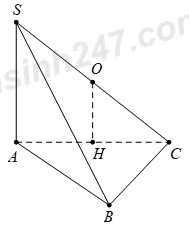
Ta có SA vuông góc với \(mp\,\,\left( ABC \right)\Rightarrow SA\bot BC\) mà \(AB\bot BC\) suy ra \(BC\bot \left( SAB \right)\) \(\Rightarrow \,\,\,BC\bot SB\,\,\,\Rightarrow \) tam giác \(SBC\) vuông tại \(B\,\,\Rightarrow \)O là trung điểm của SC. Theo bài ra, ta có \(OH\bot \left( ABC \right)\,\,\Rightarrow \,\,OH\)//\(SA\Rightarrow \,\,H\) là trung điểm của AC. Mà tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC Chọn C. Câu hỏi 4 : Cho hình chóp S.ABC có \(SA\bot \left( ABC \right).\) Gọi H, K lần lượt là trực tâm các tam giác SBC và ABC. Mệnh đề nào sau đây là sai ?
Đáp án: D Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng Lời giải chi tiết:
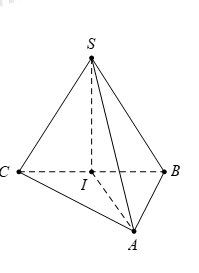
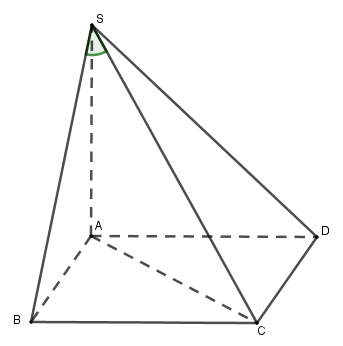
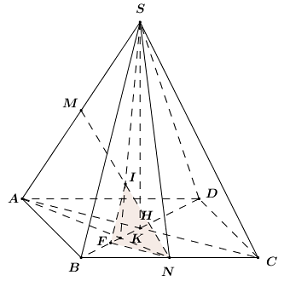
= Ta có \(\left\{ \begin{array}{l}BC \bot SA\\BC\, \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SAH} \right).\) Do đó A đúng. = Ta có \(\left\{ \begin{array}{l}CK \bot AB\\CK \bot SA\,\end{array} \right.\, \Rightarrow \,CK\, \bot \left( {SAB} \right)\, \Rightarrow CK\, \bot SB.\) Mặt khác có \(CH\bot SB.\) Từ đó suy ra \(SB\,\bot \left( CHK \right).\) Do đó B đúng. = Ta có \(\left\{ \begin{array}{l}BC \bot \left( {SAH} \right) \Rightarrow BC \bot HK\\SB\, \bot \left( {CHK} \right) \Rightarrow SB \bot HK\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right).\) Do đó C đúng. Dùng phương pháp lại trừ, suy ra D sai. Chọn D Cách khác. Từ \(CK\,\bot \left( SAB \right)\,\Rightarrow \)\(BC\) không thể vuông góc với \(\left( SAB \right).\) Câu hỏi 5 : Cho hình chóp S.ABC có \(\widehat{BSC}={{120}^{0}},\,\,\widehat{CSA}={{60}^{0}},\,\,\widehat{ASB}={{90}^{0}}\) và SA = SB = SC. Gọi I là hình chiếu vuông góc của S trên mặt phẳng (ABC), khi đó
Đáp án: D Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng Lời giải chi tiết:
Đặt SA = a Tam giác SAB vuông cân tại S, có \(AB=\sqrt{S{{A}^{2}}+S{{B}^{2}}}=a\sqrt{2}.\) Tam giác SAC cân tại S, có \(\widehat{CSA}={{60}^{0}}\) suy ra SA = SC = AC = a. Áp dụng định lí Cosin cho tam giác SBC, ta có \(B{{C}^{2}}=S{{B}^{2}}+S{{C}^{2}}-2.SB.SC.\cos \widehat{BSC}\) \(\Rightarrow \,\,B{{C}^{2}}={{a}^{2}}+{{a}^{2}}-2{{a}^{2}}.\cos {{120}^{0}}=3{{a}^{2}}\Rightarrow \,\,\,BC=a\sqrt{3}=\sqrt{A{{B}^{2}}+A{{C}^{2}}}.\) Khi đó, tam giác ABC vuông tại A mà I là hình chiếu của S trên mp(ABC). Suy ra I là tâm đường tròn ngoại tiếp tam giác ABC hay chính là trung điểm BC. Chọn D. Câu hỏi 6 : Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau. Điểm nào dưới đây cách đều bốn đỉnh A, B, C, D của tứ diện ABCD ?
Đáp án: C Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right.\,\, \Rightarrow \,\,AB \bot \left( {BCD} \right)\,\, \Rightarrow \) tam giác ABD vuông tại B. Suy ra \(OA=OB=OD=\frac{AD}{2},\) với O là trung điểm của AD. (1) Lại có \(\left\{ \begin{array}{l}AB \bot CD\\BC \bot CD\end{array} \right.\,\, \Rightarrow \,\,CD \bot \left( {ABC} \right)\,\, \Rightarrow \,\,CD \bot AC \Rightarrow \)tam giác ACD vuông tại C. Suy ra \(OA=OC=OD=\frac{AD}{2},\) với \(O\) là trung điểm của AD. (2) Từ (1), (2) suy ra trung điểm của cạnh AD cách đều A, B, C, D. Chọn C Câu hỏi 7 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, các mặt bên (SAB) và (SAD) cùng vuông góc với đáy, SA=a, góc giữa đường thẳng SC và mặt phẳng (SAB) là \(\alpha \). Khi đó \(\tan \alpha \) bằng:
Đáp án: A Phương pháp giải: Xác định góc giữa đường thẳng d và mặt phẳng (P): +) Xác định hình chiếu d’ của d trên (P). +) Góc giữa d và (P) là góc giữa d và d’ Lời giải chi tiết: Vì \(\left( SAB \right),\left( SAD \right)\) cùng vuông góc với đáy nên giao tuyến của chúng \(SA\bot \left( ABC \right)\Rightarrow SA\bot BC\). Ta có \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right)\) tại \(B\) nên hình chiếu của \(SC\) lên mặt phẳng \(\left( SBC \right)\) là \(SB\). Do đó góc giữa \(SC\) và \(\left( SBC \right)\) là góc giữa \(SC\) và \(SB\) hay góc \(\widehat{BSC}=\alpha \). \(\Delta SBC\) vuông tại \(B\) nên \(\tan \alpha =\frac{BC}{SB}\). \(\Delta SAB\) vuông tại \(A\), theo Pytago ta có \(SB=\sqrt{S{{A}^{2}}+A{{B}^{2}}}=\sqrt{{{a}^{2}}+{{a}^{2}}}=a\sqrt{2}\). \(\tan \alpha =\frac{BC}{SB}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}\). Chọn A. Câu hỏi 8 : Cho hình chóp đều \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), tâm \(O\); \(SO=2a\). Gọi \(M\) là điểm thuộc đoạn \(AO\text{ }\,\left( M\ne A;M\ne O \right)\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và vuông góc với \(AO\). Đặt \(AM=x\). Tính diện tích \(S\) của thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp \(S.ABC.\)
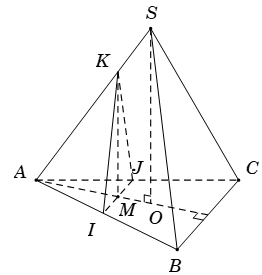
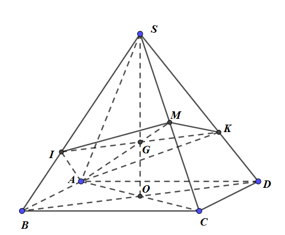
Đáp án: B Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác Lời giải chi tiết: Vì S.ABC là hình chóp đều nên \(SO\bot \left( ABC \right)\) ( với O là tâm của tam giác ABC). Do đó \(SO\bot AO\) mà \(\left( \alpha \right)\bot AO\) suy ra \(SO\parallel \left( \alpha \right)\). Tương tự ta cũng có \(BC\parallel \left( \alpha \right)\). Qua M kẻ \(IJ\parallel BC\) với \(I\in AB,\text{ }J\in AC\); kẻ \(MK\parallel SO\) với \(K\in SA.\) Khi đó thiết diện là tam giác KIJ. Diện tích tam giác KIJ là \({{S}_{\Delta IJK}}=\frac{1}{2}IJ.MK\). Trong tam giác ABC, ta có \(\frac{IJ}{BC}=\frac{AM}{AA'}\) (A’ là trung điểm của BC) suy ra \(IJ=\frac{AM.BC}{AA'}=\frac{x.a}{\frac{a\sqrt{3}}{2}}=\frac{2x\sqrt{3}}{3}\). Tương tự trong tam giác SAO, ta có \(\frac{MK}{SO}=\frac{AM}{AO}\) suy ra \(MK=\frac{AM.SO}{AO}=\frac{x.2a}{\frac{2}{3}\frac{a\sqrt{3}}{2}}=2x\sqrt{3}\). Vậy \({{S}_{\Delta IJK}}=\frac{1}{2}\frac{2x\sqrt{3}}{3}.2x\sqrt{3}=2{{x}^{2}}\). Chọn B Câu hỏi 9 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,\) \(SA=a\) và vuông góc với đáy. Mặt phẳng \(\left( \alpha \right)\) qua \(A\) và vuông góc với trung tuyến \(SI\) của tam giác \(SBC\). Tính diện tích \(S\) của thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp đã cho.
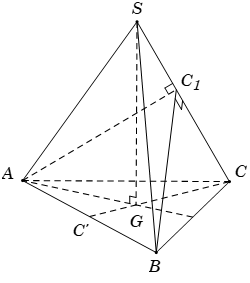
Đáp án: A Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác Lời giải chi tiết: Gọi I là trung điểm \(BC\Rightarrow AI\bot BC.\) Kẻ \(AK\bot SI\) \(\left( K\in SI \right)\). \(\Delta SAB=\Delta SAC\left( c.g.c \right)\Rightarrow SB=SC\Rightarrow \Delta SBC\) cân tại S \(\Rightarrow SI\bot BC\) Từ \(K\) kẻ đường thẳng song song với \(BC\) cắt \(SB,\text{ }SC\) lần lượt tạị \(M,\text{ }N\). \(\Rightarrow MN\bot SI\). Khi đó thiết diện là tam giác \(AMN.\) Ta có \(\left\{ \begin{align} & BC\bot AI \\ & BC\bot SA \\\end{align} \right.\Rightarrow BC\bot \left( SAI \right)\Rightarrow BC\bot AK\Rightarrow MN\bot AK.\) Tam giác vuông \(SAI\), có \(AK=\frac{SA.AI}{\sqrt{S{{A}^{2}}+A{{I}^{2}}}}=\frac{a.\frac{a\sqrt{3}}{2}}{\sqrt{{{a}^{2}}+\frac{3{{a}^{2}}}{4}}}=\frac{a\sqrt{21}}{7}\). Tam giác \(SBC\), có \(\frac{MN}{BC}=\frac{SK}{SI}=\frac{S{{A}^{2}}}{S{{I}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{I}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}+{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}}=\frac{4}{7}\Rightarrow MN=\frac{4a}{7}.\) Vậy \({{S}_{\Delta AMN}}=\frac{1}{2}AK.MN=\frac{1}{2}\frac{a\sqrt{21}}{7}.\frac{4a}{7}=\frac{2{{a}^{2}}\sqrt{21}}{49}.\) Chọn A Câu hỏi 10 : Cho hình chóp đều \(S.ABC\) có cạnh đáy bằng \(a\), cạnh bên bằng \(b\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(A\) và vuông góc với \(SC\). Tìm hệ thức giữa \(a\) và \(b\) để \(\left( \alpha \right)\) cắt \(SC\) tại điểm \({{C}_{1}}\) nằm giữa \(S\) và \(C\).
Đáp án: C Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác Lời giải chi tiết: Gọi G là trọng tâm tam giác ABC. Do S.ABC là hình chóp đều nên \(SG\bot \left( ABC \right)\). Gọi C’ là trung điểm AB. Suy ra C, C’, G thẳng hàng. Ta có \(\left\{ \begin{align} & AB\bot CC' \\ & SG\bot AB \\\end{align} \right.\Rightarrow AB\bot \left( SCC' \right)\Rightarrow AB\bot SC\). (1) Trong tam giác SAC, kẻ \(A{{C}_{1}}\bot SC\). (2) Từ (1) và (2), suy ra \(SC\bot \left( AB{{C}_{1}} \right)\). Suy ra thiết diện cần tìm là tam giác \(AB{{C}_{1}}\) thỏa mãn đi qua A và vuông góc với SC. Tam giác SAC cân tại S nên để \({{C}_{1}}\) nằm giữa S và C khi và chỉ khi \(\widehat{ASC}<{{90}^{0}}\). Suy ra \(\cos \widehat{ASC}>0\Leftrightarrow S{{A}^{2}}+S{{C}^{2}}-A{{C}^{2}}>0\Leftrightarrow 2{{b}^{2}}-{{a}^{2}}>0\Rightarrow a<b\sqrt{2}.\) Chọn C
Câu hỏi 11 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\), đáy lớn \(AD=8\), \(BC=6\), \(SA\) vuông góc với mặt phẳng \(\left( ABCD \right)\), \(SA=6.\) Gọi \(M\) là trung điểm \(AB.\) Gọi \(\left( P \right)\) là mặt phẳng qua \(M\) và vuông góc với \(AB\). Thiết diện của \(\left( P \right)\) và hình chóp có diện tích bằng:
Đáp án: C Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác Lời giải chi tiết: Do \(\left( P \right)\bot AB\Rightarrow \left( P \right)\parallel SA.\) Gọi I là trung điểm của \(SB\Rightarrow MI\parallel SA\Rightarrow MI\subset \left( P \right).\) Gọi N là trung điểm của \(CD\Rightarrow MN\bot AB\Rightarrow MN\subset \left( P \right).\) Gọi K là trung điểm của \(SC\Rightarrow IK\parallel BC\), Mà \(MN\parallel BC\Rightarrow MN\parallel IK\Rightarrow IK\subset \left( P \right).\) Vậy thiết diện của (P) và hình chóp là hình thang MNKI vuông tại M và I. Ta có: MI là đường trung bình của tam giác SAB \(\Rightarrow MI=\frac{1}{2}SA=3.\) IK là đường trung bình của tam giác SBC \(\Rightarrow IK=\frac{1}{2}BC=3.\) MN là đường trung bình của hình thang ABCD\(\Rightarrow MN=\frac{1}{2}\left( AD+BC \right)=7.\) Vậy \({{S}_{MNKI}}=\frac{IK+MN}{2}.MI=\frac{3+7}{2}.3=15.\) Chọn C.
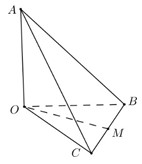
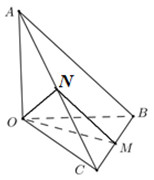
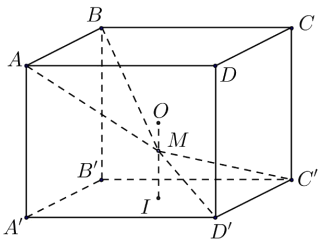
Câu hỏi 12 : Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau và \(OA = OB = OC = 1\). Gọi \(M\) là trung điểm của \(BC\) (tham khảo hình vẽ bên). Góc giữa hai đường thẳng \(OM\) và \(AB\) bằng:
Đáp án: C Phương pháp giải: Gọi \(N\) là trung điểm của \(AC \Rightarrow MN\) là đường trung bình của tam giác \( \Rightarrow MN//AB\)\( \Rightarrow \angle \left( {OM;AB} \right) = \angle \left( {OM;MN} \right)\). Lời giải chi tiết:
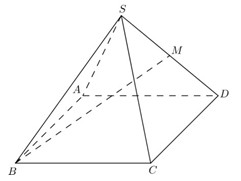
Gọi \(N\) là trung điểm của \(AC \Rightarrow MN\) là đường trung bình của tam giác \( \Rightarrow MN//AB\)\( \Rightarrow \angle \left( {OM;AB} \right) = \angle \left( {OM;MN} \right)\). Trong tam giác vuông \(OBC\) có \(OM = \dfrac{1}{2}BC = \dfrac{{\sqrt 2 }}{2}\). Trong tam giác vuông \(OAC\) có \(ON = \dfrac{1}{2}AC = \dfrac{{\sqrt 2 }}{2}\). Trong tam giác vuông \(OAB\) có \(MN = \dfrac{1}{2}AB = \dfrac{{\sqrt 2 }}{2}\). \( \Rightarrow OM = ON = MN = \dfrac{{\sqrt 2 }}{2} \Rightarrow \Delta OMN\) đều \( \Rightarrow \angle OMN = {60^0}\). Vậy \(\angle \left( {OM;AB} \right) = {60^0}\). Chọn C. Câu hỏi 13 : Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(SD\) (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng \(BM\) và mặt phẳng \(\left( {ABCD} \right)\) bằng:
Đáp án: B Phương pháp giải: Góc giữa đường thẳng và mặt phẳng cắt nhau là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. Lời giải chi tiết:
Gọi \(O = AC \cap BD\). Do chóp \(S.ABCD\) đều \( \Rightarrow SO \bot \left( {ABCD} \right)\). Trong \(\left( {SBD} \right)\) kẻ \(MH//SO\,\,\left( {H \in BD} \right) \Rightarrow MH \bot \left( {ABCD} \right)\). \( \Rightarrow \angle \left( {BM;\left( {ABCD} \right)} \right) = \angle \left( {BM;BH} \right) = \angle MBH\). \(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \). \( \Rightarrow OB = OD = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\). Dễ thấy \(MH\) là đường trung bình của \(\Delta SOD \Rightarrow H\) là trung điểm của \(OD\) và \(MH = \dfrac{1}{2}SO\). \( \Rightarrow BH = \dfrac{3}{4}BD = \dfrac{{3a\sqrt 2 }}{4}\) và \(MH = \dfrac{1}{2}SO = \dfrac{1}{2}\sqrt {S{D^2} - O{D^2}} = \dfrac{1}{2}\sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{4}\). Trong tam giác vuông \(BMH\) có: \(\tan \angle MBH = \dfrac{{MH}}{{BH}} = \dfrac{{\dfrac{{a\sqrt 2 }}{4}}}{{\dfrac{{3a\sqrt 2 }}{4}}} = \dfrac{1}{3}\). Vậy \(\tan \angle \left( {BM;\left( {ABCD} \right)} \right) = \dfrac{1}{3}\). Chọn B. Câu hỏi 14 : Cho hình lập phương \(ABCD.A'B'C'D'\). Gọi \(\alpha \) là góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABC'D'} \right)\). Khi đó:
Đáp án: D Phương pháp giải: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. Lời giải chi tiết:
Gọi \(O = A'C \cap BD' \Rightarrow O = A'C \cap \left( {ABC'D'} \right)\). Gọi \(H = A'D \cap AD'\) ta có: \(\left\{ \begin{array}{l}AB \bot \left( {ADD'A'} \right) \Rightarrow AB \bot A'H\\A'H \bot AD'\end{array} \right. \Rightarrow A'H \bot \left( {ABC'D'} \right)\) \( \Rightarrow HO\) là hình chiếu của \(A'O\) trên \(\left( {ABC'D'} \right)\) \( \Rightarrow \angle \left( {A'C;\left( {ABC'D'} \right)} \right) = \angle \left( {A'O;HO} \right) = \angle A'OH = \alpha \). Không mất tính tổng quát, ta đặt cạnh của hình lập phương bằng 1. Xét tam giác vuông \(A'OH\) vuông tại \(H\) có: \(\left\{ \begin{array}{l}OH = \dfrac{1}{2}AB = \dfrac{1}{2}\\A'H = \dfrac{1}{2}A'D = \dfrac{{\sqrt 2 }}{2}\end{array} \right. \Rightarrow \tan \angle A'OH = \tan \alpha = \dfrac{{AH}}{{OH}} = \sqrt 2 \). Chọn D Câu hỏi 15 : Cho hình chóp đều \(S.ABCD\) có tất cả các cạnh bằng a, điểm M là trung điểm cạnh SMặt phẳng \(\left( P \right)\) chứa \(AM\) và song song \(BD\). Tính diện tích thiết diện của hình chóp \(S.ABCD\) cắt bởi \(\left( P \right)\).
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên \(SO \bot \left( {ABCD} \right)\) Gọi G là giao điểm của AM và SO. Qua G, dựng IK // BD, \(\left( {I \in SB,K \in SD} \right)\)\( \Rightarrow \left( {AIMK} \right) \equiv \left( P \right)\). Thiết diện của hình chóp \(S.ABCD\) cắt bởi \(\left( P \right)\) là tứ giác\(AIMK\). Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\). Mà IK // BD\( \Rightarrow IK \bot \left( {SAC} \right) \Rightarrow IK \bot AM \Rightarrow {S_{AIMK}} = \dfrac{1}{2}.IK.AM\) \(\Delta SAC\) có \(SA = SC = a,\,\,AC = a\sqrt 2 \Rightarrow \Delta SAC\) vuông cân tại S, \(AM = \sqrt {S{A^2} + S{M^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}\) G là trọng tâm \( \Rightarrow \dfrac{{SG}}{{SO}} = \dfrac{2}{3} \Rightarrow \dfrac{{IK}}{{BD}} = \dfrac{2}{3} \Rightarrow IK = \dfrac{2}{3}.a\sqrt 2 = \dfrac{{2a\sqrt 2 }}{3}\) \( \Rightarrow {S_{AIMK}} = \dfrac{1}{2}.\dfrac{{2a\sqrt 2 }}{3}.\dfrac{{a\sqrt 5 }}{2} = \dfrac{{{a^2}\sqrt {10} }}{3}\). Chọn: B Câu hỏi 16 : Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(2a.\) Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp \(S.ABCD\) bằng \(\dfrac{{4{a^3}}}{3}\) . Gọi \(\alpha \) là góc giữa \(SC\) và mặt đáy, tính \(\tan \alpha .\)
Đáp án: D Phương pháp giải: Xác định đường cao bằng kiến thức \(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a \bot d;\,a \subset \left( P \right)\end{array} \right. \Leftrightarrow a \bot \left( Q \right)\) Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(d\) và đường thẳng \(d'\) là hình chiếu của \(d\) lên mặt phẳng \(\left( P \right).\) Thể tích khối chóp \(V = \dfrac{1}{3}S.h\) Lời giải chi tiết: Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot AB\) (do \(\Delta SAB\) cân tại \(S\)) Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \bot AB;\,\,\,SH \subset \left( {SAB} \right)\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\) Hay \(H\) là hình chiếu của \(S\) lên mặt phẳng \(\left( {ABCD} \right) \Rightarrow CH\) là hình chiều của .. lên mặt phẳng \(\left( {ABCD} \right)\) Do đó góc giữa \(SC\) và mặt đáy là góc \(SCH.\) Ta có \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} \Leftrightarrow \dfrac{{4{a^3}}}{3} = \dfrac{1}{3}SH.4{a^2} \Leftrightarrow SH = a\). Xét tam giác \(BHC\) vuông tại \(B\), theo định lý Pytago ta có \(HC = \sqrt {B{H^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \) Xét tam giác \(SHC\) vuông tại \(H\) có \(\tan \angle SCH = \dfrac{{SH}}{{HC}} = \dfrac{a}{{a\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}\). Chọn D. Câu hỏi 17 : Cho hình chóp \(S.ABC\) có SA vuông góc với mặt phẳng (ABC), \(SA = 2a\), tam giác ABC vuông tại B, \(AB = a\), \(BC = a\sqrt 3 \). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng
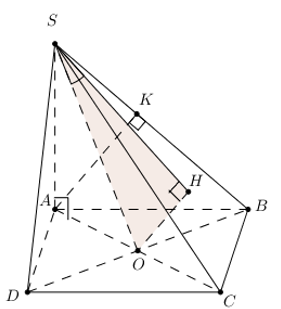
Đáp án: D Phương pháp giải: Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) là góc giữa \(d\) và \(d'\) với \(d'\) là hình chiếu của \(d\) trên mặt phẳng \(\left( P \right)\) Sử dụng tỉ số lượng giác của góc nhọn để suy ra số đo góc. Lời giải chi tiết: Ta có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) \( \Rightarrow \)\(A\) là hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) \( \Rightarrow \)\(AC\) là hình chiếu của \(SC\) lên mặt phẳng \(\left( {ABC} \right)\) Từ đó góc giữa \(SC\) và mặt phẳng \(\left( {ABC} \right)\) là \(\widehat {SCA}\) Vì \(\Delta ABC\) vuông tại B \( \Rightarrow A{C^2} = A{B^2} + B{C^2} = {a^2} + 3{a^2} = 4{a^2}\)\( \Rightarrow AC = 2a\) Xét tam giác \(SAC\) vuông tại \(A\) có \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{2a}}{{2a}} = 1 \Rightarrow \widehat {SCA} = {45^o}\). Vậy góc cần tìm bằng \(45^\circ .\) Chọn D. Câu hỏi 18 : Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a\sqrt 2 \); \(BC = a\) và \(SA = SB = SC = SD = 2a\). Gọi \(K\) là hình chiếu vuông góc của \(B\) trên \(AC\), \(H\) là hình chiếu vuông góc của \(K\) trên \(SA\). Tính cosin góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {BKH} \right)\).\(\)\(\)
Đáp án: A Phương pháp giải: - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. - Sử dụng định lí Cosin trong tam giác để tính góc. Lời giải chi tiết:
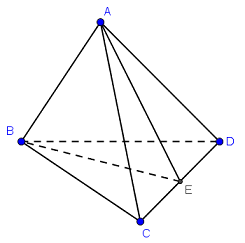
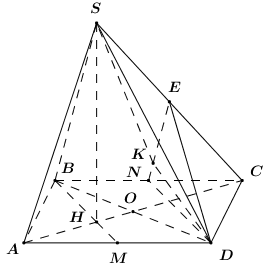
Gọi \(O = AC \cap BD\). Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật (tâm \(O\)), \(SA = SB = SC = SD\)\( \Rightarrow SO \bot \left( {ABCD} \right).\) Ta có: \(\left\{ \begin{array}{l}BK \bot AC\\BK \bot SO\end{array} \right. \Rightarrow BK \bot \left( {SAC} \right) \Rightarrow BK \bot SA\). Mà \(SA \bot HK\,\,\left( {gt} \right) \Rightarrow SA \bot \left( {BHK} \right)\). \( \Rightarrow SH \bot \left( {BHK} \right)\) \( \Rightarrow HB\) là hình chiếu của \(SB\) lên \(\left( {BHK} \right)\). \( \Rightarrow \angle \left( {SB;\left( {BHK} \right)} \right) = \angle \left( {SB;HB} \right) = \angle SBH\). Xét tam giác \(SAB\) có: \({\rm{cos}}\angle ASB = \dfrac{{S{A^2} + S{B^2} - AB}}{{2.SA.SB}} = \dfrac{{4{{\rm{a}}^2} + 4{{\rm{a}}^2} - 2{{\rm{a}}^2}}}{{2.2{\rm{a}}.2{\rm{a}}}} = \dfrac{3}{4}\) \( \Rightarrow \sin \angle ASB = \dfrac{{\sqrt 7 }}{4} \Rightarrow \cos \angle SBH = \dfrac{{\sqrt 7 }}{4}\) (Do \(\angle ASB < {90^0}\)). Chọn: A. Câu hỏi 19 : Tứ diện \(ABCD\) có hai mặt \(ABC\) và \(ABD\) là các tam giác đều. Góc giữa \(AB\) và \(CD\) là:
Đáp án: C Phương pháp giải: \(\left\{ \begin{array}{l}a \bot b,\,a \bot c\\b,c \subset \left( \alpha \right)\\b \cap c = \left\{ I \right\}\end{array} \right. \Rightarrow a \bot \left( \alpha \right)\) ; \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\\forall b,\,\,b \subset \left( \alpha \right)\end{array} \right. \Rightarrow a \bot b\) Lời giải chi tiết:
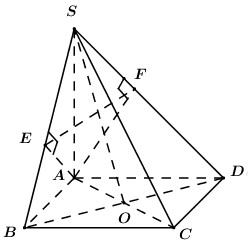
Gọi \(E\) là trung điểm của \(CD\). Vì \(ABC\) và \(ABD\) là các tam giác đều nên \(AB = AC = AD = BC = BD.\) \( \Rightarrow \Delta ACD,\,\,\Delta BCD\) cân lần lượt tại các đỉnh \(A,\,\,B\). \( \Rightarrow \left\{ \begin{array}{l}AE \bot CD\\BE \bot CD\end{array} \right. \Rightarrow CD \bot \left( {ABE} \right) \Rightarrow CD \bot AB\) \( \Rightarrow \left( {AB;CD} \right) = {90^0}.\) Chọn C. Câu hỏi 20 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Gọi AE, AF lần lượt là các đường cao của tam giác SAB và tam giác SAD. Chọn khẳng định đúng trong các khẳng định sau:
Đáp án: D Phương pháp giải: Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\), \(\left\{ \begin{array}{l}d \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow d \bot a\). Lời giải chi tiết:
+ \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AE\) . + \(\left\{ \begin{array}{l}AE \bot BC\,\,\left( {cmt} \right)\\AE \bot SB\,\,\,\left( {gt} \right)\end{array} \right. \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow AE \bot SC\). + CMTT: \(AF \bot SC\). + \(\left\{ \begin{array}{l}SC \bot AE\\SC \bot AF\end{array} \right. \Rightarrow SC \bot \left( {AEF} \right)\). Chọn D. Câu hỏi 21 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy, \(SA = a\sqrt 2 \). Gọi \(M,\,\,N\) lần lượt là hình chiếu vuông góc của điểm \(A\) trên các cạnh \(SB,\,\,SD\). Góc giữa mặt phẳng \(\left( {AMN} \right)\) và đường thẳng \(SB\) bằng:
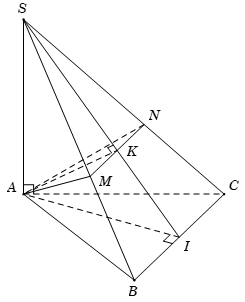
Đáp án: D Phương pháp giải: - Tìm giao điểm \(P\) của \(SC\) và \(\left( {AMN} \right)\), chứng minh \(SP \bot \left( {AMN} \right)\). - Góc giữa đường và mặt là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó. - Sử dụng hệ thức lượng và tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Lời giải chi tiết:
Gọi \(O = AC \cap BD\), trong \(\left( {SBD} \right)\) gọi \(E = MN \cap SO\). Trong \(\left( {SAC} \right)\) kéo dài \(AE\) cắt \(SC\) tại \(P\), khi đó ta có \(\left( {AMN} \right) \cap SC = P\). Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\). \(\left\{ \begin{array}{l}AM \bot SB\,\,\left( {gt} \right)\\AN \bot BC\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right)\) \( \Rightarrow AM \bot SC\). Chứng minh tương tự ta có \(AN \bot \left( {SCD} \right) \Rightarrow AN \bot SC\). \( \Rightarrow AC \bot \left( {SMN} \right)\) tại \(P\). Do đó \(PM\) là hình chiếu của \(SM\) lên \(\left( {AMN} \right)\). \( \Rightarrow \angle \left( {SB;\left( {AMN} \right)} \right) = \angle \left( {SM;\left( {AMN} \right)} \right) = \angle \left( {SM;PM} \right) = \angle SMP\). Áp dụng hệ thức lượng trong tam giác vuông \(SAB\) ta có: \(SM = \dfrac{{S{A^2}}}{{SB}} = \dfrac{{S{A^2}}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2{a^2}}}{{\sqrt {2{a^2} + {a^2}} }} = \dfrac{{2a}}{{\sqrt 3 }}\) Áp dụng hệ thức lượng trong tam giác vuông \(SAC\) ta có: \(SP = \dfrac{{S{A^2}}}{{SC}} = \dfrac{{S{A^2}}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{2{a^2}}}{{\sqrt {2{a^2} + 2{a^2}} }} = a\). Xét tam giác \(SMP\) vuông tại \(P\) có \(\sin \angle SMP = \dfrac{{SP}}{{SM}} = \dfrac{a}{{\dfrac{{2a}}{{\sqrt 3 }}}} = \dfrac{{\sqrt 3 }}{2}\)\( \Rightarrow \angle SMP = {60^0}\). Vậy góc giữa mặt phẳng \(\left( {AMN} \right)\) và đường thẳng \(SB\) bằng \({60^0}\). Chọn D. Câu hỏi 22 : Cho hình chóp tứ giác đều \(S.ABCD\) có đáy là hình vuông tâm \(O\); cạnh \(a\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(SA\) và \(BC\). Góc giữa đường thẳng \(MN\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^0}\). Tính cos của góc giữa đường thẳng \(MN\) và mặt phẳng \(\left( {SBD} \right)\) ?
Đáp án: C Phương pháp giải: Lời giải chi tiết:
Gọi \(H\) là trung điểm của \(OA\) ta có \(MH\parallel SO \Rightarrow MH \bot \left( {ABCD} \right)\). \( \Rightarrow HN\) là hình chiếu của \(MN\) lên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {MN;\left( {ABCD} \right)} \right) = \angle \left( {MN;HN} \right) = \angle MNH = {60^0}\). Xét tam giác \(CHN\) có: \(CN = \dfrac{1}{2}BC = \dfrac{a}{2}\), \(CH = \dfrac{3}{4}AC = \dfrac{{3a\sqrt 2 }}{4}\), \(\angle HCN = {45^0}\). \(\begin{array}{l} \Rightarrow H{N^2} = C{H^2} + C{N^2} - 2CH.CN.\cos {45^0}\\\,\,\,\,\,\,\,H{N^2} = \dfrac{{9{a^2}}}{8} + \dfrac{{{a^2}}}{4} - 2.\dfrac{{3a\sqrt 2 }}{4}.\dfrac{a}{2}.\dfrac{{\sqrt 2 }}{2}\\\,\,\,\,\,\,\,H{N^2} = \dfrac{{5{a^2}}}{8} \Rightarrow HN = \dfrac{{a\sqrt {10} }}{4}\end{array}\) Xét tam giác vuông \(MNH\) có: \(MN = \dfrac{{NH}}{{\cos {{60}^0}}} = \dfrac{{a\sqrt {10} }}{2}\). Trong \(\left( {SAC} \right)\) gọi \(E = CM \cap SO\) \( \Rightarrow \left( {MBC} \right) \cap \left( {SBD} \right) = BE\). Trong \(\left( {MBC} \right)\) gọi \(I = MN \cap BE \Rightarrow I = MN \cap \left( {SBD} \right)\). Gọi \(K\) là trung điểm của \(OB\) \( \Rightarrow NK\parallel OC\). Ta có: \(\left\{ \begin{array}{l}OC \bot BD\\OC \bot SO\end{array} \right. \Rightarrow OC \bot \left( {SBD} \right) \Rightarrow NK \bot \left( {SBD} \right)\). \( \Rightarrow IK\) là hình chiếu của \(IN\) lên \(\left( {SBD} \right)\). \( \Rightarrow \angle \left( {MN;\left( {SBD} \right)} \right) = \angle \left( {IN;\left( {SBD} \right)} \right) = \angle \left( {IN;IK} \right) = \angle NIK\). Ta có \(NK = \dfrac{1}{2}OC = \dfrac{{a\sqrt 2 }}{4}\). Áp dụng định lí Menelaus trong tam giác \(MAC\) ta có: \(\dfrac{{EM}}{{EC}}.\dfrac{{OC}}{{OA}}.\dfrac{{SA}}{{SM}} = 1\) \( \Leftrightarrow \dfrac{{EM}}{{EC}}.1.2 = 1 \Leftrightarrow \dfrac{{EM}}{{EC}} = \dfrac{1}{2}\). Áp dụng định lí Menelaus trong tam giác \(MNC\) ta có: \(\dfrac{{IM}}{{IN}}.\dfrac{{BN}}{{BC}}.\dfrac{{EC}}{{EM}} = 1 \Leftrightarrow \dfrac{{IM}}{{IN}}.\dfrac{1}{2}.2 = 1 \Leftrightarrow IM = IN\). \( \Rightarrow IN = \dfrac{1}{2}MN = \dfrac{{a\sqrt {10} }}{4}\). Xét tam giác vuông \(INK\) có: \(sin\angle NIK = \dfrac{{NK}}{{IN}} = \dfrac{{a\sqrt 2 }}{4}:\dfrac{{a\sqrt {10} }}{4} = \dfrac{1}{{\sqrt 5 }}\). Vậy \(\cos \angle NIK = \sqrt {1 - {{\sin }^2}\angle NIK} = \sqrt {1 - \dfrac{1}{5}} = \dfrac{{2\sqrt 5 }}{5}\). Chọn C. Câu hỏi 23 : Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a,\,\,SA = a\sqrt 3 \). Gọi \(G\) là trọng tâm tam giác \(SCD\) và \(\alpha \) là góc giữa đường thẳng \(BG\) và \(SA\). Tính \(\cos \alpha \).
Đáp án: A Phương pháp giải: +) Gọi \(M\) là trung điểm của \(CD\), \(O = AC \cap BD,\,\,H = AM \cap OD\). Chứng minh \(\angle \left( {BG;SA} \right) = \angle \left( {BG;HG} \right)\). +) Áp dụng định lí Cosin trong tam giác. Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(CD\), \(O = AC \cap BD,\,\,H = AM \cap OD\). Chọn A. Câu hỏi 24 : Trong mặt phẳng (P) cho hình vuông ABCD cạnh \(a\). Trên đường thẳng qua A và vuông góc với mặt phẳng (P) lấy điểm S sao cho \(SA = a\). Mặt cầu đường kính AC cắt các đường thẳng SB, SC, SD lần lượt tại \(M \ne B,\,\,N \ne C,\,\,P \ne D\). Tính diện tích tứ giác AMNP?
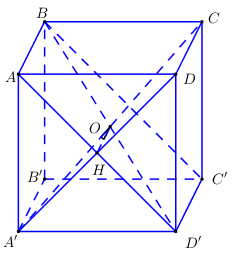
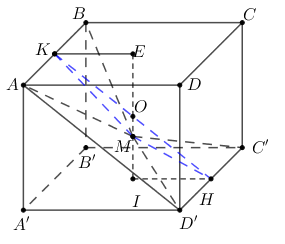
Đáp án: D Phương pháp giải: +) Chứng minh \(SC \bot \left( {AMNP} \right)\). +) Sử dụng công thức tỉ số thể tích tính thể tích chóp S.AMNP. +) Sử dụng công thức tính thể tích \({V_{S.AMNP}} = \dfrac{1}{3}SN.{S_{AMNP}} \Rightarrow {S_{AMNP}} = \dfrac{{3{V_{S.AMNP}}}}{{SN}}\). Lời giải chi tiết: Gọi \(O = AC \cap BD\). Do M thuộc mặt cầu đường kính AC \( \Rightarrow \widehat {AMC} = {90^0} \Rightarrow MC \bot MA\). Ta có \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\) \( \Rightarrow AM \bot \left( {SBC} \right) \Rightarrow AM \bot SB\) và \(AM \bot SC\). Chứng minh tương tự ta có \(AP \bot \left( {SCD} \right) \Rightarrow AP \bot SC;\,\,AP \bot SD\). N thuộc mặt cầu đường kính \(AC \Rightarrow \widehat {ANC} = {90^0} \Rightarrow AN \bot SC\). \( \Rightarrow SC \bot \left( {AMNP} \right)\). Áp dụng hệ thức lượng trong tam giác vuông SAC ta có \(SN = \dfrac{{S{A^2}}}{{SC}} = \dfrac{{S{A^2}}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{{a^2}}}{{\sqrt {{a^2} + 2{a^2}} }} = \dfrac{a}{{\sqrt 3 }}\) và \(\dfrac{{SN}}{{SC}} = \dfrac{{S{A^2}}}{{S{C^2}}} = \dfrac{{{a^2}}}{{{a^2} + 2{a^2}}} = \dfrac{1}{3}\). Áp dụng hệ thức lượng trong tam giác vuông SAB ta có \(\dfrac{{SM}}{{SB}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{{a^2}}}{{{a^2} + {a^2}}} = \dfrac{1}{2}\). Áp dụng hệ thức lượng trong tam giác vuông SAD ta có \(\dfrac{{SP}}{{SD}} = \dfrac{{S{A^2}}}{{S{D^2}}} = \dfrac{{{a^2}}}{{{a^2} + {a^2}}} = \dfrac{1}{2}\). Ta có: \(\begin{array}{l}\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6} \Rightarrow {V_{S.AMN}} = \dfrac{1}{6}{V_{S.ABC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\\dfrac{{{V_{S.ANP}}}}{{{V_{S.ACD}}}} = \dfrac{{SN}}{{SC}}.\dfrac{{SP}}{{SD}} = \dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6} \Rightarrow {V_{S.ANP}} = \dfrac{1}{6}{V_{S.ACD}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\ \Rightarrow {V_{S.AMNP}} = {V_{S.AMN}} + {V_{S.ANP}} = \dfrac{1}{{12}}{V_{S.ABCD}} + \dfrac{1}{{12}}{V_{S.ABCD}} = \dfrac{1}{6}{V_{S.ABCD}} = \dfrac{1}{6}.\dfrac{1}{3}.SA.{S_{ABCD}} = \dfrac{{{a^3}}}{{18}}\end{array}\) Lại có \({V_{S.AMNP}} = \dfrac{1}{3}SN.{S_{AMNP}} \Rightarrow {S_{AMNP}} = \dfrac{{3{V_{S.AMNP}}}}{{SN}} = \dfrac{{3.\dfrac{{{a^3}}}{{18}}}}{{\dfrac{a}{{\sqrt 3 }}}} = \dfrac{{{a^2}\sqrt 3 }}{6}\). Chọn D. Câu hỏi 25 : Cho hình lập phương ABCD. A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho \(MO = \frac{1}{2}MI\) (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
Đáp án: D Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. Lời giải chi tiết:
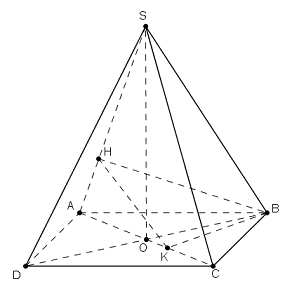
Nhận thấy giao tuyến (d) của hai mặt phẳng \(\left( {MAB} \right),\left( {MC'D'} \right)\) là đường thẳng đi qua \(M\) và song song với \(AB,C'D'\) Do \(M\in OI\Rightarrow MA=MB\Rightarrow \Delta MAB\) cân tại M, tương tự \(\Delta MC'D'\) cân tại M. Gọi K, H lần lượt là trung điểm của AB và C’D’ ta có: Do đó \(MK \bot AB \Rightarrow MK \bot d;MH \bot C'D' \Rightarrow MH \bot d\) Khi đó \(\left( {\left( {MC'D'} \right),\left( {MAB} \right)} \right) = \left( {MH,MK} \right) = \varphi \Rightarrow \cos \varphi = \left| {\cos \widehat {HMK}} \right|\) Giả sử hình lập phương có cạnh bằng \(6\) Ta có: \(IM=2,IH=3\Rightarrow MH=\sqrt{13}\) Gọi \(E\) là tâm hình vuông \(ABCD \Rightarrow EM = 4;EK = 3 \Rightarrow MK = \sqrt {{4^2} + {3^2}} = 5\) Mà \(HK = AD' = 6\sqrt 2 \) Suy ra \(\left| {\cos \widehat {HMK}} \right| = \left| {\frac{{M{K^2} + M{H^2} - H{K^2}}}{{2MH.MK}}} \right| = \left| {\frac{{25 + 13 - 72}}{{2.5\sqrt {13} }}} \right| = \left| {\frac{{ - 34}}{{10\sqrt {13} }}} \right| = \frac{{17\sqrt {13} }}{{65}}\) Vậy \(\cos \varphi =\frac{17\sqrt{13}}{65}\) Chọn D. Câu hỏi 26 : Chóp S.ABCD, \(SA\bot \left( ABCD \right),\,SA=a,\,\,ABCD\) là hình vuông cạnh a tâm O. Tính \(\widehat{\left( SO;\left( SBC \right) \right)}\) ?
Đáp án: B Phương pháp giải: Lời giải chi tiết: * Vẽ giả tưởng \(OH\bot \left( SBC \right)\Rightarrow \widehat{\left( SO;\left( SBC \right) \right)}=\widehat{\left( SO;SH \right)}=\widehat{OSH}\). * Tính + Tam giác vuông SAO : \(AO=\frac{a\sqrt{2}}{2}\Rightarrow SO=\sqrt{{{a}^{2}}+\frac{2{{a}^{2}}}{4}}=\frac{a\sqrt{6}}{2}\) + \(OH=d\left( O;\left( SBC \right) \right)=\frac{1}{2}d\left( A;\left( SBC \right) \right)=\frac{1}{2}AK=\frac{1}{2}\frac{a\sqrt{2}}{2}=\frac{a\sqrt{2}}{4}\) + Tam giác vuông SHO : \(\sin \widehat{OSH}=\frac{OH}{SO}=\frac{a\sqrt{2}}{4}:\frac{a\sqrt{6}}{2}=\frac{1}{2\sqrt{3}}\). Chọn đáp án B. Câu hỏi 27 : Cho hình chóp \(S.ABCD\) đều tất cả các cạnh bằng \(a\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(SA,\,\,BC\).Tính \({\rm{cosin}}\) góc giữa \(MN\) và mặt phẳng \(\left( {SBD} \right)\).
Đáp án: D Phương pháp giải: Lời giải chi tiết:
Gọi \(AC \cap BD = \left\{ H \right\} \Rightarrow SH \bot \left( {ABCD} \right).\) Ta có: \(\left\{ \begin{array}{l}AC \bot BD\,\,\left( {gt} \right)\\AC \bot SH\,\,\left( {SH \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow AC \bot \left( {SBD} \right)\) Gọi F là trung điểm của BH \( \Rightarrow NF\parallel AC\) (Do \(NF\) là đường trung bình của tam giác \(BCH\)). Mà \(AC \bot \left( {SBD} \right)\) \( \Rightarrow NF \bot \left( {SBD} \right).\) Trong mặt phẳng \(\left( {ABCD} \right)\) gọi \(AN \cap BD = \left\{ K \right\}\) Trong mặt phẳng \(\left( {SAN} \right)\) gọi \(SK \cap MN = \left\{ I \right\}\) \( \Rightarrow I = MN \cap \left( {SBD} \right)\). \( \Rightarrow \angle \left( {MN;\left( {SBD} \right)} \right) = \angle \left( {NI;\left( {SBD} \right)} \right)\). Ta có: \(FI\) là hình chiếu của \(MI\) lên \(\left( {SBD} \right)\) \( \Rightarrow \angle \left( {NI;\left( {SBD} \right)} \right) = \angle \left( {NI;FI} \right) = \angle NIF\). Xét tam giác \(ABC\) có \(K\) là giao điểm của hai đường trung tuyến \(AN\) và \(BH\) nên \(K\) là trọng tâm của tam giác \(ABC\). Áp dụng định lí Menelaus trong tam giác \(AMN\), cát tuyến \(SIK\) có: \(\dfrac{{SM}}{{SA}}.\dfrac{{KA}}{{KN}}.\dfrac{{IN}}{{IM}} = 1\) \( \Leftrightarrow \dfrac{1}{2}.2.\dfrac{{IN}}{{IM}} = 1 \Leftrightarrow \dfrac{{IN}}{{IM}} = 1\) \( \Rightarrow IM = IN\) \( \Rightarrow I\) là trung điểm của \(MN\). Ta có: \(NF = \dfrac{{HC}}{2} = \dfrac{{AC}}{4} = \dfrac{{a\sqrt 2 }}{4}\)(Tính chất đường trung bình của tam giác). Tam giác \(SBC\) đều cạnh \(a\) nên \(SN = \dfrac{{a\sqrt 3 }}{2}.\) Tam giác \(ABN\) vuông tại \(B\) nên áp dụng định lí Pytago ta có: \(A{N^2} = A{B^2} + B{N^2} = {a^2} + {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{5{a^2}}}{4}.\) Tam giác \(SAN\) có trung tuyến \(MN\) nên: \(\begin{array}{l}M{N^2} = \dfrac{{A{N^2} + S{N^2}}}{2} - \dfrac{{S{A^2}}}{4} = \dfrac{{\dfrac{{3{a^2}}}{4} + \dfrac{{5{a^2}}}{4}}}{2} - \dfrac{{{a^2}}}{4} = \dfrac{{3{a^2}}}{4}.\\ \Rightarrow MN = \dfrac{{a\sqrt 3 }}{2}\end{array}\) \( \Rightarrow NI = \dfrac{{MN}}{2} = \dfrac{{a\sqrt 3 }}{4}.\) Vì \(FN \bot \left( {SBD} \right) \Rightarrow FN \bot FI \Rightarrow \Delta FNI\) vuông tại \(F\). \(\begin{array}{l} \Rightarrow \sin \angle FIN = \dfrac{{NF}}{{NI}} = \dfrac{{a\sqrt 2 }}{4}:\dfrac{{a\sqrt 3 }}{4} = \dfrac{{\sqrt 2 }}{{\sqrt 3 }}\\ \Rightarrow \cos \angle FIN = \sqrt {1 - {{\sin }^2}\angle FIN} = \dfrac{{\sqrt 3 }}{3}.\end{array}\) Chọn D. Câu hỏi 28 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\), góc \(\angle BAD = {60^0}\), \(SA = SB = SD = \dfrac{{a\sqrt 3 }}{2}\). Gọi \(\alpha \) là góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( {SBC} \right)\). Giá trị \(\cos \alpha \) bằng:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Xét tam giác \(ABD\) có: \(\left\{ \begin{array}{l}AB = AD\\\angle BAD = {60^0}\end{array} \right.\) \( \Rightarrow \Delta ABD\) đều. Gọi \(H\) là trọng tâm \(\Delta ABD\), do \(SA = SB = SD\) nên \(SH \bot \left( {ABCD} \right)\).
Gọi \(M\) là trung điểm của \(AD\), ta có \(BM \bot AD \Rightarrow BM \bot BC\). Ta có: \(\left\{ \begin{array}{l}BC \bot BM\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SBM} \right)\). Goi \(N,\,\,E\) lần lượt là trung điểm của \(BC\) và \(SC\) ta có: \(\left\{ \begin{array}{l}BN\parallel DM\\BN = DM\end{array} \right. \Rightarrow BNDM\) là hình bình hành \( \Rightarrow DN\parallel BM\). Lại có \(NE\) là đường trung bình của tam giác \(SBC\) nên \(NE\parallel SB\). \( \Rightarrow \left( {NDE} \right)\parallel \left( {SBM} \right)\). Mà \(BC \bot \left( {SBM} \right)\) nên \(BC \bot \left( {NDE} \right)\). Trong \(\left( {NDE} \right)\) kẻ \(DK \bot NE\,\,\,\left( {K \in NE} \right)\) ta có: \(\left\{ \begin{array}{l}DK \bot NE\\DK \bot BC\,\,\left( {BC \bot \left( {NDE} \right)} \right)\end{array} \right.\)\( \Rightarrow DK \bot \left( {SBC} \right)\). \( \Rightarrow \) Hình chiếu của \(SD\) lên \(\left( {SBC} \right)\) là \(SK\). \( \Rightarrow \angle \left( {SD;\left( {SBC} \right)} \right) = \angle \left( {SD;SK} \right) = \angle DSK\). Xét tam giác \(SHA\) có \(AH = \dfrac{2}{3}AO = \dfrac{{a\sqrt 3 }}{3}\), \(SA = \dfrac{{a\sqrt 3 }}{2}\). Áp dụng định lí Pytago ta có: \(SH = \sqrt {S{A^2} - A{H^2}} = \dfrac{{a\sqrt {15} }}{6}\). Ta có: \(AC = 2AO = a\sqrt 3 \) \( \Rightarrow HC = AC - AH = \dfrac{{2a\sqrt 3 }}{3}\). Áp dụng định lí Pytago trong tam giác vuông \(SHC\) ta có: \(SC = \sqrt {S{H^2} + H{C^2}} = \dfrac{{a\sqrt 7 }}{2}\). Xét tam giác \(SCD\) có: \(\begin{array}{l}D{E^2} = \dfrac{{S{D^2} + C{D^2}}}{2} - \dfrac{{S{C^2}}}{4}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\dfrac{{3{a^2}}}{4} + {a^2}}}{2} - \dfrac{{7{a^2}}}{{16}}\\ \Rightarrow DE = \dfrac{{a\sqrt 7 }}{4}\end{array}\) Xét tam giác \(DNE\) ta có: \(DN = BM = \dfrac{{a\sqrt 3 }}{2}\), \(NE = \dfrac{1}{2}SB = \dfrac{{a\sqrt 3 }}{4}\), \(DE = \dfrac{{a\sqrt 7 }}{4}\). Gọi \(p\) là nửa chu vi tam giác \(DNE\) ta có: \(p = \dfrac{{\sqrt 7 + 3\sqrt 3 }}{8}\). Diện tích tam giác \(DNE\) là: \({S_{DNE}} = \sqrt {p\left( {p - DN} \right)\left( {p - DE} \right)\left( {p - NE} \right)} = \dfrac{{{a^2}\sqrt 5 }}{{16}}\). Lại có \({S_{DNE}} = \dfrac{1}{2}DK.NE \Rightarrow DK = \dfrac{{2{S_{DNE}}}}{{NE}} = \dfrac{{a\sqrt {15} }}{6}\). Ta có: \(DK \bot \left( {SBC} \right) \Rightarrow DK \bot SK\). \( \Rightarrow \Delta SDK\) vuông tại \(K\), suy ra \(\sin \angle DSK = \dfrac{{DK}}{{SD}} = \dfrac{{\dfrac{{a\sqrt {15} }}{6}}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{\sqrt 5 }}{3}\). Vậy \(\cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } = \dfrac{2}{3}\). Chọn C. Câu hỏi 29 : Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và độ dài cạnh bên SA = SB = SC = b. Gọi G là trọng tâm của tam giác ABC. Độ dài đoạn thẳng SG bằng
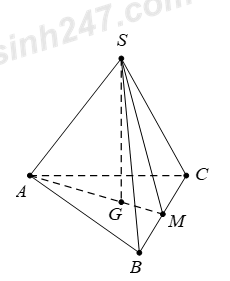
Đáp án: C Phương pháp giải: Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và định lý Pytago Lời giải chi tiết:
Vì SA = SB = SC và G là trọng tâm tam giác ABC Suy ra G là chân đường cao kẻ từ đỉnh S xuống mặt phẳng (ABC). Gọi M là trung điểm của BC suy ra \(BM=CM=\frac{BC}{2}=\frac{a}{2}.\) Tam giác ABC đều cạnh a, có \(GM=\frac{AM}{3}=\frac{a\sqrt{3}}{2}.\frac{1}{3}=\frac{a\sqrt{3}}{6}.\) Tam giác SBM vuông tại M, có \(SM=\sqrt{S{{B}^{2}}-M{{B}^{2}}}=\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{4}}.\) Tam giác SGM vuông tại G, có \(SG=\sqrt{S{{M}^{2}}-G{{M}^{2}}}=\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{4}-\frac{{{a}^{2}}}{12}}=\frac{\sqrt{9{{b}^{2}}-3{{a}^{2}}}}{3}.\) Chọn C.
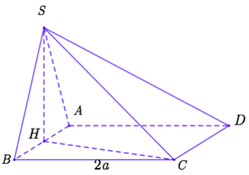
Câu hỏi 30 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, BC = a. Cạnh bên SA vuông góc với mặt phẳng đáy, đường thẳng SC tạo với các mặt phẳng (SAB) và (ABCD) các góc đều bằng \({30^0}.\) Tính diện tích S của hình chữ nhật ABCD.
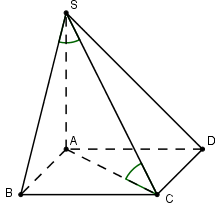
Đáp án: C Phương pháp giải: Áp dụng phương pháp tìm góc giữa đường thẳng và mặt phẳng – hệ thức lượng trong tam giác vuông để giải quyết yêu cầu của bài toán Lời giải chi tiết: Vì \(SA \bot \left( {ABCD} \right) \Rightarrow \,\,AC\) là hình chiếu vuông góc của SC trên (ABCD) \( \Rightarrow \) Góc giữa đường thẳng SC và mặt phẳng (ABCD) là \(\widehat {SCA} = {30^0}.\) Ta có \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow \,\,BC \bot \left( {SAB} \right)\,\, \Rightarrow \,\,SB\) là hình chiếu vuông góc của SC trên (SAB). \( \Rightarrow \) Góc giữa đường thẳng SC và mặt phẳng (SAB) là \(\widehat {BSC} = {30^0}.\) Đặt \(AB = x\,\, \Rightarrow \,\,AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{x^2} + {a^2}} \,\, \Rightarrow \,\,\left\{ \begin{array}{l}SA = AC.\tan \widehat {SCA} = \sqrt {\frac{{{x^2} + {a^2}}}{3}} \\SB = \frac{{BC}}{{\tan \widehat {BSC}}} = a\sqrt 3\end{array} \right.\) Tam giác SAB vuông tại \(A\,\, \Rightarrow \,\,S{A^2} + A{B^2} = S{B^2}\)\( \Leftrightarrow \,\,\frac{{{x^2} + {a^2}}}{3} + {x^2} = 3{a^2} \Leftrightarrow \frac{4}{3}{x^2} = \frac{8}{3}{a^2} \Leftrightarrow x = a\sqrt 2 .\) Vậy diện tích hình chữ nhật ABCD là \(S = AB\,\, \times \,BC = {a^2}\sqrt 2 .\) Chọn C.
|