Lời giải chi tiết:

Hướng dẫn giải chi tiết:

Ta có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \Rightarrow {\sin ^2}\alpha  = 1 - {\cos ^2}\alpha  = 1 - {\left( {\dfrac{{ - 12}}{{13}}} \right)^2} = \dfrac{{25}}{{169}} \Rightarrow {\text{ }}\sin \alpha  =  \pm \dfrac{5}{{13}}\)

Vì \(\dfrac{\pi }{2} < \alpha  < \pi \) nên \(\sin \alpha  > 0 \Rightarrow {\text{sin}}\alpha  = \dfrac{5}{{13}} \Rightarrow \tan \alpha  = \dfrac{{\sin \alpha }}{{{\text{cos}}\alpha }} = \dfrac{{ - 5}}{{12}}\).

Chọn D

Lời giải chi tiết:

Hướng dẫn giải chi tiết:

\(P = m\sin {0^0} + {\rm{ }}n\cos {0^0}{\rm{ }} + {\rm{ }}p\sin {90^0} = {\rm{ }}m.0{\rm{ }} + {\rm{ }}n.1{\rm{ }} + {\rm{ }}p.1{\rm{ }} = n{\rm{ }} + {\rm{ }}p\)

Chọn D

Lời giải chi tiết:

Hướng dẫn giải chi tiết:

\(Q = m\cos {90^0} + {\text{ }}n\sin {90^0}{\text{ }} + {\text{ }}p\sin {180^0} = m.0 + n.1 + p.0 = n\).

Chọn B

Lời giải chi tiết:

Hướng dẫn giải chi tiết:

\(S = 3 - {\sin ^2}{90^0} + 2{\cos ^2}{60^0} - 3{\tan ^2}{45^0} = 3 - {1^2} + 2.{\left( {\dfrac{1}{2}} \right)^2} - {3.1^2} = \dfrac{{ - 1}}{2}\).

Chọn B

Lời giải chi tiết:

Hướng dẫn giải chi tiết:

\(\sin {120^0} = \dfrac{{\sqrt 3 }}{2} \Rightarrow {\cos ^2}{120^0} = 1 - {\sin ^2}{120^0} \Rightarrow {\cos ^2}{120^0} = \dfrac{1}{4}\)

Vì \({90^0} < {120^0} < {180^0} \Rightarrow \cos {120^0} < 0 \Rightarrow \cos {120^0} = \dfrac{{ - 1}}{2}\). Sai ở bước (IV).

Chọn D

Phương pháp giải:

Lời giải chi tiết:

Hướng dẫn giải chi tiết:

\({\sin ^6}x + {\cos ^6}x = {({\sin ^2}x + {\cos ^2}x)^3} - 3{\sin ^2}x{\cos ^2}x({\sin ^2}x + {\cos ^2}x) = 1 - 3{\sin ^2}x{\cos ^2}x\).

Chọn D

Phương pháp giải:

Số điểm \(M\) trên đường tròn định hướng bằng số giá trị của k thỏa mãn \(0 \le \) sđ cung \(AM\)  \( \le 2\pi \) 

Lời giải chi tiết:

Ta có: \(0 \le \,sd\,\,cung\,\,AM \le 2\pi  \Leftrightarrow 0 \le \frac{\pi }{6} + \frac{{k2\pi }}{3} \le 2\pi  \Leftrightarrow  - \frac{\pi }{6} \le \frac{{k2\pi }}{3} \le \frac{{11\pi }}{6}\)

\( \Leftrightarrow  - \frac{1}{6} \le \frac{{2k}}{3} \le \frac{{11}}{6} \Leftrightarrow  - \frac{3}{{12}} \le k \le \frac{{11}}{4}\)  mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;\,1;\,2} \right\}.\) 

Vậy có 3 điểm \(M\)  thỏa mãn yêu cầu đề bài.

Chọn C.

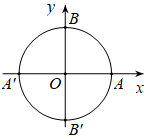
Phương pháp giải:

Xác định điểm cuối và chu kỳ của cung lượng giác đó.

Lời giải chi tiết:

Ta có điểm đầu là A \(\left( {{0^o}} \right)\) và cứ \({90^o} = \frac{\pi }{2}\) là góc đó lại quét đến điểm B, A’ ,B’.

\( \Rightarrow \) Số đo của cung lượng giác đó là \(\frac{{k\pi }}{2},\,\,k \in \mathbb{Z}.\)

Chọn B.

Phương pháp giải:

Sử dụng công thức tính độ dài cung \(\alpha \) của đường tròn bán kính R là \(l = \alpha R\).

Lời giải chi tiết:

Ta có \(l = \alpha R \Rightarrow 2R = \alpha R \Rightarrow \alpha  = 2\).

Chọn B

Phương pháp giải:

Sử dụng công thức tính độ dài cung \(\alpha \) của đường tròn bán kính R là \(l = \alpha R\).

Lời giải chi tiết:

Độ dài nửa đường tròn bán kính R là \(\pi R\).

Do đó độ dài cung đã cho là \(l = \dfrac{1}{6}\pi R\).

Ta có \(l = \alpha \pi  \Rightarrow \dfrac{1}{6}\pi R = \alpha R \Rightarrow \alpha  = \dfrac{\pi }{6}\).

Chọn D

Phương pháp giải:

\(\alpha  \in \left( { - 18; - 12} \right) \Rightarrow  - 18 < \alpha  <  - 12\), tìm các giá trị nguyên của k thỏa mãn.

Lời giải chi tiết:

Theo bài ra ta có: \(\alpha  = \dfrac{{11\pi }}{5} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\), \(\alpha  \in \left( { - 18; - 12} \right)\)

\( \Rightarrow  - 18 < \dfrac{{11\pi }}{5} + k\pi  <  - 12 \Leftrightarrow \dfrac{{ - 18 - \dfrac{{11\pi }}{5}}}{\pi } < k < \dfrac{{ - 12 - \dfrac{{11\pi }}{5}}}{\pi } \Leftrightarrow  - 7,93 < k <  - 6,01\).

Mà \(k \in \mathbb{Z} \Rightarrow k =  - 7 \Rightarrow \alpha  = \dfrac{{11\pi }}{5} - 7\pi  =  - \dfrac{{24\pi }}{5}\).

Chọn B

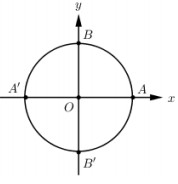
Phương pháp giải:

Biểu diễn cung trên đường tròn lượng giác.

Lời giải chi tiết:

Ta có \(\dfrac{{2\pi }}{\pi } = 2 \Rightarrow \alpha  = k\pi \) được biểu diễn bởi 2 điểm trên đường tròn lượng giác.

Cho \(k = 0 \Rightarrow \alpha  = 0,\,\,k = 1 \Rightarrow \alpha  = \pi \).

Vậy cung lượng giác \(\alpha  = k\pi \) được biểu diễn bởi điểm A và A’ trên đường tròn lượng giác.

Chọn C

Phương pháp giải:

Số vòng = Quãng đường đi được : Chu vi

Lời giải chi tiết:

Quãng đường xe đi được trong 1 giây = \(\dfrac{1}{{3600}}\) giờ là: \(50.\dfrac{1}{{3600}} = \dfrac{1}{{72}}\,\,\left( {km} \right) = \dfrac{{12500}}{9}\,\,\left( {cm} \right)\).

Chu vi của bánh xe là \(C = 2\pi .R = 2\pi .\dfrac{{55}}{2} = 55\pi \,\,\left( {cm} \right)\).

Vậy số vòng bánh xe quay được trong 1 giây là \(n = \dfrac{{\dfrac{{12500}}{9}}}{{55\pi }} \approx 8,04\) (vòng)

Chọn A

Phương pháp giải:

Hai cung có số đo lần lượt là \(\alpha ,\,\,\beta \)có điểm đầu và điểm cuối trung nhau khi chúng sai khác nhau nguyên lần \(2\pi \).

Lời giải chi tiết:

Xét hiệu

\(\begin{array}{l}\alpha  - \beta  = \dfrac{{ - 5\pi }}{6} - \dfrac{\pi }{3} =  - \dfrac{{7\pi }}{6}\\\alpha  - \gamma  = \dfrac{{ - 5\pi }}{6} - \dfrac{{25\pi }}{3} =  - \dfrac{{55\pi }}{6}\\\alpha  - \delta  = \dfrac{{ - 5\pi }}{6} - \dfrac{{19\pi }}{6} =  - 4\pi \\\beta  - \gamma  = \dfrac{\pi }{3} - \dfrac{{25\pi }}{3} =  - 8\pi  =  - 4\left( {2\pi } \right)\\\beta  - \delta  = \dfrac{\pi }{3} - \dfrac{{19\pi }}{6} =  - \dfrac{{17\pi }}{6}\\\gamma  - \delta  = \dfrac{{25\pi }}{3} - \dfrac{{19\pi }}{6} = \dfrac{{31\pi }}{6}\end{array}\)

Vậy \(\alpha \) và \(\delta \), \(\beta \) và \(\gamma \) có điểm đầu và điểm cuối trung nhau.

Chọn B.

Phương pháp giải:

Giá trị tổng quát của một góc lượng giác được viết ở dạng \(\alpha  + k2\pi \) trong đó \(0 \le \alpha  \le 2\pi \).

Lời giải chi tiết:

\(\dfrac{{3\pi }}{2} + 2017\pi  = \dfrac{\pi }{2} + \pi  + 2017\pi  = \dfrac{\pi }{2} + 1009\left( {2\pi } \right)\).

Vậy giá trị tổng quát của góc lượng giác \(\left( {Ox;Oy} \right)\) là: \(\dfrac{\pi }{2} + k2\pi \).

Chọn C

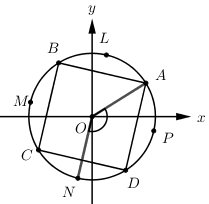
Phương pháp giải:

Khi quay điểm A một góc \( - \dfrac{{3\pi }}{4}\)theo chiều âm của đường tròn định hướng, ta được góc \(\widehat {AON}\).

Vậy điểm cuối của \(\alpha \) trùng với điểm N.

Chọn A

Lời giải chi tiết:

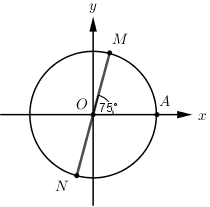
Phương pháp giải:

Sử dụng công thức tính độ dài cung \(\alpha \) của đường tròn bán kính R là \(l = \alpha R\).

Lời giải chi tiết:

Bánh xe đã quay được khi di chuyển 10 răng tức là quay được một cung tròn có độ dài \(l = \dfrac{{10}}{{72}}.2\pi R = \dfrac{5}{{18}}\pi R\).

Mà \(l = \alpha R \Rightarrow \alpha R = \dfrac{5}{{18}}\pi R \Rightarrow \alpha  = \dfrac{5}{{18}}\pi  = {50^0}\).

Chọn C

Phương pháp giải:

Tính số đo góc AON

Lời giải chi tiết:

Ta có \(\widehat {AOM} + \widehat {AON} = {180^0}\) (kề bù) \( \Rightarrow \widehat {AON} = {180^0} - {75^0} = {105^0}\).

Vậy số đo của góc lượng giác AN bằng \( - {105^0}\).

Chọn D

Phương pháp giải:

Với \(\frac{\pi }{2} < \alpha  < \pi \) ta có: \(\sin \alpha  > 0,\,\,\,\cos \alpha  < 0.\)

Lời giải chi tiết:

Với \(\frac{\pi }{2} < \alpha  < \pi \) thì \(\cos \alpha  < 0.\)

Ta có: \(\left| {\cos \alpha } \right| = \sqrt {1 - {{\sin }^2}\alpha }  = \sqrt {1 - {{\left( {\frac{5}{{13}}} \right)}^2}}  = \frac{{12}}{{13}},\) mà \(\cos \alpha  < 0\) nên \(\cos \alpha  =  - \frac{{12}}{{13}}.\)

\( \Rightarrow A = 3\cos \alpha  + 2\sin \alpha  = 3.\left( { - \frac{{12}}{{13}}} \right) + 2.\frac{5}{{13}} =  - 2.\)

Chọn C.

Phương pháp giải:

Chia cả tử và mẫu cho \({\cos ^2}\alpha \) rồi tính giá trị của biểu thức.

Lời giải chi tiết:

\(\begin{array}{l}B = \frac{{1 + 5\sin \alpha \cos \alpha }}{{3 - 2{{\cos }^2}\alpha }} = \frac{{\frac{1}{{{{\cos }^2}\alpha }} + 5.\frac{{\sin \alpha .\cos \alpha }}{{{{\cos }^2}\alpha }}}}{{3.\frac{1}{{{{\cos }^2}\alpha }} - 2.\frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}}}\\\,\,\,\,\, = \frac{{1 + {{\tan }^2}\alpha  + 5\tan \alpha }}{{3\left( {1 + {{\tan }^2}\alpha } \right) - 2}} = \frac{{1 + {2^2} + 5.2}}{{3\left( {1 + {2^2}} \right) - 2}} = \frac{{15}}{{13}}.\end{array}\)

Chọn A.