20 bài tập trắc nghiệm cung lượng giác và góc lượng giác mức độ thông hiểuLàm bàiCâu hỏi 1 : Cho biểu thức \(P = 3{\sin ^2}x + 4{\cos ^2}x\), biết \(\cos x = \dfrac{1}{2}\). Giá trị của \(P\) bằng:
Đáp án: D Lời giải chi tiết: Hướng dẫn giải chi tiết: \(P = 3{\sin ^2}x + 4{\cos ^2}x = 3({\sin ^2}x + {\cos ^2}x) + {\cos ^2}x = 3 + {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{{13}}{4}\). Chọn D Câu hỏi 2 : Nếu \(\tan \alpha + \cot \alpha = 2\) thì \(\tan^2\alpha + {\text{ }}\cot^2\alpha \) bằng:
Đáp án: C Lời giải chi tiết: Hướng dẫn giải chi tiết: \(\tan \alpha + \cot \alpha = 2 \Rightarrow {(\tan \alpha + \cot \alpha )^2} = 4 \Rightarrow {\tan ^2}\alpha + 2\tan \alpha \cot \alpha + {\cot ^2}\alpha = 4 \Rightarrow {\tan ^2}\alpha + {\cot ^2}\alpha = 2\) Chọn C Câu hỏi 3 : Cho \(\sin \alpha = \dfrac{1}{3}{\text{ (}}\dfrac{\pi }{2} < \alpha < \pi )\). Giá trị \(\tan \alpha \) là?
Đáp án: A Lời giải chi tiết: Hướng dẫn giải chi tiết: Ta có \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha \Rightarrow {\cos ^2}\alpha = \dfrac{8}{9} \Rightarrow \cos \alpha = \pm \dfrac{{2\sqrt 2 }}{3}\) Vì \(\dfrac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha = \dfrac{{ - 2\sqrt 2 }}{3} \Rightarrow \tan \alpha = \dfrac{{\sin \alpha }}{{{\text{cos}}\alpha }} = \dfrac{{ - \sqrt 2 }}{4}\). Chọn A Câu hỏi 4 : Cho \(\cos \alpha = \dfrac{{ - 2}}{3}{\text{ (18}}{{\text{0}}^0} < \alpha < {270^0})\). Trong các khẳng định sau khẳng định nào đúng?
Đáp án: A Lời giải chi tiết: Hướng dẫn giải chi tiết: Ta có \({\sin ^2}\alpha = 1 - {\cos ^2}\alpha \Rightarrow {\sin ^2}\alpha = \dfrac{5}{9} \Rightarrow \sin \alpha = \pm \dfrac{{\sqrt 5 }}{3}\) Vì \({180^0} < \alpha < {270^0} \Rightarrow \sin \alpha = \dfrac{{ - \sqrt 5 }}{3} \Rightarrow \cot \alpha = \dfrac{{{\text{cos}}\alpha }}{{\sin \alpha }} = \dfrac{{2\sqrt 5 }}{5}\). Chọn A Câu hỏi 5 : Kết quả đơn giản của biểu thức \({\left( {\dfrac{{\sin \alpha + \tan \alpha }}{{{\text{cos}}\alpha {\text{ + 1}}}}} \right)^2} + 1\) bằng:
Đáp án: C Lời giải chi tiết: Hướng dẫn giải chi tiết: \({\left( {\dfrac{{\sin \alpha + \tan \alpha }}{{\cos \alpha + 1}}} \right)^2} + 1 = {\left( {\dfrac{{\sin \alpha + \dfrac{{\sin \alpha }}{{\cos \alpha }}}}{{\cos \alpha + 1}}} \right)^2} + 1 = \dfrac{{{{\sin }^2}\alpha {{(\cos \alpha + 1)}^2}}}{{{{\cos }^2}\alpha {{(\cos \alpha + 1)}^2}}} + 1 = {\tan ^2}\alpha + 1 = \dfrac{1}{{{{\cos }^2}\alpha }}\) Chọn C Câu hỏi 6 : Cho \(A = \cos {235^0}.\sin {60^0}.\tan {125^0}.\cos {90^0}{\text{ }}\). Khẳng định nào sau đây đúng?
Đáp án: B Lời giải chi tiết: Hướng dẫn giải chi tiết: Vì \(\cos {90^0} = 0\) nên \(A = \cos {235^0}.\sin {60^0}.\tan {125^0}.\cos {90^0} = 0\). Chọn B Câu hỏi 7 : Biểu thức \(P = {\cos ^2}x.{\cot ^2}x{\text{ }} + 3{\cos ^2}x - {\cot ^2}x + 2{\sin ^2}x\) có giá trị là:
Đáp án: A Lời giải chi tiết: Hướng dẫn giải chi tiết:
\(\begin{array}{l}P = {\cos ^2}x.{\cot ^2}x{\rm{ }} + 3{\cos ^2}x - {\cot ^2}x + 2{\sin ^2}x\\{\rm{ }} = {\cot ^2}x\left( {{{\cos }^2}x - 1} \right) + {\cos ^2}x + 2\left( {{{\cos }^2}x + {{\sin }^2}x} \right)\\{\rm{ }} = \dfrac{{{{\cos }^2}x}}{{{{\sin }^2}x}}.( - {\sin ^2}x) + {\cos ^2}x + 2\\{\rm{ }} = - {\cos ^2}x + {\cos ^2}x + 2 = 2\end{array}\) Chọn A Câu hỏi 8 : Giá trị lớn nhất của \(6{\cos ^2}x + 6\sin x-2\) là:
Đáp án: C Lời giải chi tiết: Hướng dẫn giải chi tiết: Ta có: \(\begin{array}{l}6{\cos ^2}x + 6\sin x - 2 = 6(1 - {\sin ^2}x) + 6\sin x - 2\\ = - 6{\sin ^2}x + 6\sin x + 4\\ = - 6({\sin ^2}x - \sin x) + 4\\ = - 6{\left( {\sin x - \dfrac{1}{2}} \right)^2} + \dfrac{{11}}{2} \le \dfrac{{11}}{2}\end{array}\) Dấu “=” xảy ra khi \(\sin x = \dfrac{1}{2}\). Chọn C Câu hỏi 9 : Trên đường tròn lượng giác, cho điểm M với \(AM = 1\) như hình vẽ dưới đây. Số đo cung AM là:
Đáp án: B Phương pháp giải: Trên đường tròn lượng giác, tính từ chiều dương trục hoành, ngược chiều kim đồng hồ là chiều dương, xuôi chiều kim đồng hồ là chiều âm. Lời giải chi tiết: Dễ thấy \(OA = OM = AM = 1 \Rightarrow \Delta OAM\) đều \( \Rightarrow \angle AOM = {60^o} = \frac{\pi }{3}\) Vì M nằm dưới trục hoành \( \Rightarrow \) Số đo cung AM \( = - \frac{\pi }{3} + k2\pi ,\,\,\,\,k \in \mathbb{Z}\) Chọn B. Câu hỏi 10 : Trên đường tròn lượng giác gốc A, cho điểm M xác định bởi sđ cung \(AM = \frac{\pi }{3}\). Gọi \({M_1}\) là điểm đối xứng của M qua trục Ox. Tìm số đo cung lượng giác \(A{M_1}.\)
Đáp án: C Phương pháp giải: 2 góc lượng giác có 2 điểm cuối đối xứng với nhau qua trục Ox là 2 góc đối nhau Lời giải chi tiết: Do \({M_1}\) là điểm đối xứng của M qua trục Ox mà sđ cung \(AM = \frac{\pi }{3}\) \( \Rightarrow sd\,\,cung\,\,A{M_1} = - \frac{\pi }{3} + k2\pi ,\,\,\,k \in \mathbb{Z}\) Chọn C. Câu hỏi 11 : Cho đường tròn \((O)\) đường kính bằng \(10\,{\rm{cm}}\). Tính độ dài cung có số đo \(\frac{{7\pi }}{{12}}.\)
Đáp án: D Phương pháp giải: Độ dài cung tròn \(l = R.n\) với R là bán kính và n là số đo cung (rad). Lời giải chi tiết: Cho đường tròn \((O)\) đường kính bằng \(10\,{\rm{cm}}\). Độ dài cung có số đo \(\frac{{7\pi }}{{12}}\) là \(l = 5.\frac{{7\pi }}{{12}} = \frac{{35\pi }}{{12}}\,\,(cm)\) Chọn D. Câu hỏi 12 : Trên đường tròn lượng giác, gọi \(M\) là điểm biểu diễn của cung lượng giác \(\alpha = - {15^0}.\) Trong các cung lượng giác biểu diễn bởi điểm \(M\), hãy cho biết cung có số đo dương nhỏ nhất là bao nhiêu?
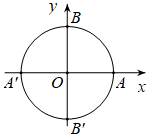
Đáp án: D Phương pháp giải: Viết số đo cung lượng giác tổng quát, từ đó thay từng giá trị của k để tìm cung có số đo dương nhỏ nhất Lời giải chi tiết: \(M\) là điểm biểu diễn của cung lượng giác \(\alpha = - {15^0}.\) \( \Rightarrow \) Số đo cung lượng giác biểu diễn bởi điểm \(M\) \( = - {15^o} + k{.360^o}\,\,\,\,\,\,\,(k \in \mathbb{Z})\) Dễ thấy để cung có số đo dương nhỏ nhất \( \Leftrightarrow k = 1\) Khi đó số đo cung là \( - {15^o} + {360^o} = {345^o}\) Chọn D. Câu hỏi 13 : Trên đường tròn lượng giác (gốc \(A\)), cung lượng giác có số đo \(\alpha = - {90^0} + k{360^0}\,\,\,(k \in Z)\) có điểm cuối trùng với điểm nào sau đây ?
Đáp án: A Phương pháp giải: Trên đường tròn lượng giác, ngược chiều kim đồng hồ là chiều dương, xuôi chiều kim đồng hồ là chiều âm. Lời giải chi tiết: Trên đường tròn lượng giác (gốc \(A\)), cung lượng giác có số đo \(\alpha = - {90^0} + k{360^0}\,\,\,(k \in Z)\) có điểm cuối trùng với điểm \(B'\) Chọn A. Câu hỏi 14 : Tính độ dài cung tròn có bán kính R = 20cm và có số đo 1350.
Đáp án: C Phương pháp giải: Độ dài cung tròn \(l = \frac{{\pi R{n^o}}}{{{{180}^o}}}\) Lời giải chi tiết: \(l = \frac{{\pi R{n^o}}}{{{{180}^o}}} = \frac{{\pi {{.20.135}^o}}}{{{{180}^o}}} = 15\pi \) cm Chọn C. Câu hỏi 15 : Góc \(\alpha = \frac{\pi }{3} + k\pi ,k \in \mathbb{Z}\). Khi đó \(\alpha \) được biểu diễn bởi mấy điểm trên đường tròn lượng giác?
Đáp án: D Phương pháp giải: Xác định chu kỳ, một vòng tròn là \(2\pi .\) Lời giải chi tiết: Ta có: \(\alpha = \frac{\pi }{3} + k\pi ,k \in \mathbb{Z}\) có chu kỳ là \(\pi \) \( \Rightarrow \) Số điểm trên đường tròn lượng giác biểu diễn \(\alpha \) là \(\left[ {\frac{{2\pi }}{\pi }} \right] = 2\) Chọn D. Câu hỏi 16 : Đổi số đo của góc \( - \dfrac{{3\pi }}{{16}}\,\,rad\) sang đơn vị độ, phút, giây.
Đáp án: C Phương pháp giải: \(\alpha \,\,\left( {rad} \right) = \alpha .{\left( {\dfrac{{180}}{\pi }} \right)^0}\) Lời giải chi tiết: \( - \dfrac{{3\pi }}{{16}}\,\,rad = - \dfrac{3}{{16}}{.180^0} = {\left( { - \dfrac{{135}}{4}} \right)^0} = - {33^0}45'\). Chọn C Câu hỏi 17 : Khẳng định nào sau đây đúng khi nói về "góc lượng giác" ?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Trên đường tròn định hướng, góc hình học AOB có phân biệt điểm đầu A và điểm cuối B là góc lượng giác. Chọn D Câu hỏi 18 : Mệnh đề nào sau đây đúng ?
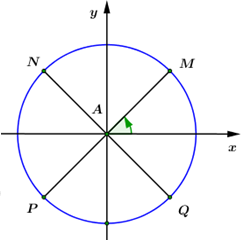
Đáp án: B Phương pháp giải: Sử dụng công thức tính độ dài cung \(\alpha \) của đường tròn bán kính R là \(l = \alpha R\). Lời giải chi tiết: Công thức tính độ dài cung \(\alpha \) của đường tròn bán kính R là \(l = \alpha R\). Do đó Độ dài cung tròn tỉ lệ với bán kính của nó. Chọn B Câu hỏi 19 : Trên đường tròn lượng giác gốc \(A,\) bốn điểm chính giữa bốn cung phần tư thứ \(\left( I \right),\left( {II} \right),\left( {III} \right),\left( {IV} \right)\) biểu diễn các cung lượng giác có số đo nào sau đây?
Đáp án: C Phương pháp giải: Vẽ đường tròn lượng giác để tìm số đo của các cung. Lời giải chi tiết:
Trên đường tròn lượng giác gốc A, bốn điểm chính giữa bốn cung phần tư thứ \(\left( I \right),\left( {II} \right),\left( {III} \right),\left( {IV} \right)\) biểu diễn các cung lượng giác có số đo \(\frac{\pi }{4} + k\frac{\pi }{2}\). Chọn C. Câu hỏi 20 : Trên đường tròn lượng giác gốc \(A,\) có bao nhiêu điểm \(M\) thỏa mãn số đo cung lượng giác \(cungAM\) bằng \(\frac{\pi }{6} + k\frac{\pi }{5},\) với \(k\) là số nguyên.
Đáp án: B Phương pháp giải: Lời giải chi tiết: Có \(0 \le \frac{\pi }{6} + k\frac{\pi }{5} \le 2\pi \Leftrightarrow - \frac{5}{6} \le k \le \frac{{55}}{6} \Rightarrow k \in \left\{ {0;1;2;...;9} \right\}\). Vậy có 10 giá trị nguyên của \(k.\) Chọn B.
|
