20 bài tập trắc nghiệm cung lượng giác và góc lượng giác mức độ nhận biếtLàm bàiCâu hỏi 1 : Cho góc \(x\) thoả \({0^0} < x < {90^0}\) . Trong các mệnh đề sau, mệnh đề nào sai:
Đáp án: B Lời giải chi tiết: Hướng dẫn giải chi tiết: Vì \({0^0} < x < {90^0}\) nên \(\sin x > 0,\cos x > 0,\tan {\text{ }}x > 0,\cot x > 0\) Suy ra \(\cos x < 0\) sai. Chọn B Câu hỏi 2 : Cho góc \(x\) thoả \({90^0} < x < {180^0}\) . Trong các mệnh đề sau, mệnh đề nào đúng:
Đáp án: A Lời giải chi tiết: Hướng dẫn giải chi tiết: Vì \({90^0} < x < {180^0}\) nên \(\sin x > 0,\cos x < 0,\tan x < 0,\cot x < 0\) Chọn A Câu hỏi 3 : Kết quả nào sau đây đúng?
Đáp án: C Lời giải chi tiết: Hướng dẫn giải chi tiết: Ta có \(\pi {\text{ }}ra{\text{d}} = {180^0} \Rightarrow 1{\text{ rad}} = {\left( {\dfrac{{180}}{\pi }} \right)^0}\). Chọn C Câu hỏi 4 : Trên đường tròn tùy ý, cung có số đo \(1\,rad\) là:
Đáp án: B Phương pháp giải: Áp dụng công thức tính độ dài cung: \(l = \alpha .R\), trong đó \(\alpha \) là số đo cung (rad) và R là bán kính. Lời giải chi tiết: Cung có số đo 1rad có độ dài: \(l = \alpha .R = 1.R = R\) Chọn: B Câu hỏi 5 : Kết quả nào sau đây đúng?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chọn: B Câu hỏi 6 : Trên đường tròn có bán kính \(r = 5\), độ dài của cung có số đo \({\pi \over 8}\) là:
Đáp án: B Phương pháp giải: Cung có số đo \(\alpha \,\,rad\) của đường tròn bán kính R có độ dài: \(l = R\alpha \). Lời giải chi tiết: \(l = R\alpha = 5.{\pi \over 8} = {{5\pi } \over 8}\) Chọn: B Câu hỏi 7 : Trên đường tròn lượng giác, khẳng định nào sau đây là đúng?
Đáp án: D Phương pháp giải: Sử dụng khái niệm cung lượng giác. Lời giải chi tiết: Chọn: D Câu hỏi 8 : Giá trị của \(\tan {180^0}\) bằng
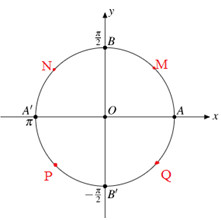
Đáp án: B Phương pháp giải: Sử dụng MTBT hoặc đường tròn lượng giác. Lời giải chi tiết: \(\tan {180^0} = 0\). Chọn: B. Câu hỏi 9 : Cung \(\alpha \) có điểm đầu là A, điểm cuối trùng với một trong bốn điểm M, N, P, Q (như hình vẽ) . Số đo của cung \(\alpha \) là:
Đáp án: D Phương pháp giải: Cho lần lượt các điểm cuối là M, N, P, Q và rút ra quy luật. Lời giải chi tiết: Khi điểm cuối là M ta có: \(\alpha = {\pi \over 4} + k2\pi \,\,\left( {k \in Z} \right)\) Khi điểm cuối là N thì \(\alpha = {{3\pi } \over 4} + k2\pi \,\,\left( {k \in Z} \right)\) Khi diểm cuối là P thì \(\alpha = {{5\pi } \over 4} + k2\pi \,\,\left( {k \in Z} \right)\) Khi điểm cuối là Q thì \(\alpha = {{7\pi } \over 4} + k2\pi \,\,\left( {k \in Z} \right)\) \( \Rightarrow \alpha = {\pi \over 4} + {{k\pi } \over 2}\,\,\left( {k \in Z} \right)\) Chọn: D Câu hỏi 10 : Góc \({{5\pi } \over 6} = ?\)
Đáp án: A Phương pháp giải: \(\pi = {180^0}\) Lời giải chi tiết: \({{5\pi } \over 6} = {5 \over 6}{.180^0} = {150^0}\) Chọn: A Câu hỏi 11 : Góc \(\frac{{5\pi }}{6}\) có số đo theo độ là
Đáp án: D Phương pháp giải: \(\pi = {180^o}\) Lời giải chi tiết: \(\frac{{5\pi }}{6} = \frac{{{{5.180}^o}}}{6} = {150^o}\) Chọn D. Câu hỏi 12 : Khẳng định nào sau đây là đúng khi nói về “đường tròn định hướng”?
Đáp án: D Phương pháp giải: Sử dụng định nghĩa đường tròn định hướng. Lời giải chi tiết: Mỗi đường tròn trên đó ta chọn một chiều chuyển động gọi là chiều dương và chiều ngược lại được gọi là chiều âm là một đường tròn định hướng. Chọn D. Câu hỏi 13 : Quy ước chọn chiều dương của một đường tròn định hướng là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Quy ước chọn chiều dương của một đường tròn định hướng luôn ngược chiều quay kim đồng hồ. Chọn B Câu hỏi 14 : Trên đường tròn lượng giác cung có số đo 1 rad là:
Đáp án: D Phương pháp giải: Sử dụng công thức tính độ dài cung \(\alpha \) của đường tròn bán kính R là \(l = \alpha R\). Lời giải chi tiết: Trên đường tròn lượng giác cung có số đo 1 rad là: \(l = 1.R = R\). Chọn D Câu hỏi 15 : Nếu một cung tròn có số đo là \({a^0}\) thì số đo radian của nó là:
Đáp án: C Phương pháp giải: \(\pi = {180^0}\) Lời giải chi tiết: Ta có \(\pi = {180^0} \Rightarrow {a^0} = \dfrac{{a\pi }}{{180}}\,\,\left( {rad} \right)\). Chọn C Câu hỏi 16 : Đổi số đo của góc \({108^0}\) sang đơn vị radian.
Đáp án: A Phương pháp giải: Nếu một cung tròn có số đo là \({a^0}\) thì số đo radian của nó là: \(\dfrac{{a\pi }}{{180}}\). Lời giải chi tiết: \({108^0} = \dfrac{{108\pi }}{{180}} = \dfrac{{3\pi }}{5}\,\,\left( {rad} \right)\). Chọn A Câu hỏi 17 : Đổi số đo của góc \(\dfrac{\pi }{{12}}\,\,rad\) sang đơn vị độ, phút, giây.
Đáp án: A Phương pháp giải: \(\alpha \,\,\left( {rad} \right) = \alpha .{\left( {\dfrac{{180}}{\pi }} \right)^0}\) Lời giải chi tiết: \(\dfrac{\pi }{{12}}\,\,rad = {\left( {\dfrac{{180}}{{12}}} \right)^0} = {15^0}\). Chọn A Câu hỏi 18 : Tính độ dài \(l\) của cung trên đường tròn có số đo bằng 1,5 và bán kính bằng 20cm.
Đáp án: A Phương pháp giải: Sử dụng công thức tính độ dài cung \(\alpha \) của đường tròn bán kính R là \(l = \alpha R\). Lời giải chi tiết: \(l = 1,5.20 = 30\,\,\left( {cm} \right)\) Chọn A Câu hỏi 19 : Mệnh đề nào trong các mệnh đề sau đây sai?
Đáp án: D Phương pháp giải: Quan hệ lượng giác giữa các cung đặc biệt. Lời giải chi tiết: Ta có: \(\cos \left( { - \alpha } \right) = \cos \alpha \Rightarrow \) D sai. Chọn D. Câu hỏi 20 : Trên đường tròn định hướng có bán kính bằng \(4\) lấy một cung có số đo bằng \(\frac{\pi }{3}\) rad. Độ dài của cung tròn đó là:
Đáp án: A Phương pháp giải: Sử dụng công thức \(l = R.\alpha \) với \(R\) là bán kính đường tròn, \(\alpha \,\,rad\) là số đo cung. Lời giải chi tiết: Ta có: \(l = R.\alpha = 4.\frac{\pi }{3} = \frac{{4\pi }}{3}\) Chọn A.
|