Đề số 9 - Đề kiểm tra học kì 1 - Toán 7Đáp án và lời giải chi tiết Đề số 9 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 7 Đề bài I. Trắc nghiệm: (2.0 điểm)Khoanh tròn vào chữ cái đứng trước câu trả lời đúng nhất. Câu 1 :Kết quả phép tính \(\dfrac{3}{4} + \dfrac{1}{4} \cdot \dfrac{{ - 12}}{{20}}\) là A.\(\dfrac{{ - 12}}{{20}}\) B.\(\dfrac{3}{5}\) C.\(\dfrac{{ - 3}}{5}\) D.\(\dfrac{{ - 9}}{{84}}\) Câu 2 :Giá trị của biểu thức: \(\left| { - 3,4} \right|:\left| {1,7} \right| - 0,2\) là: A.\( - 1,8\) B.\(1,8\) C.\(0\) D.\( - 2,2\) Câu 3 : Nếu các số \(a,\,\,b,\,\,c,\,\,d\) khác \(0\) thỏa mãn \(ad = bc\) thì tỉ lệ thức nào sau đây không đúng? A.\(\dfrac{a}{b} = \dfrac{c}{d}\) B.\(\dfrac{a}{c} = \dfrac{b}{d}\) C.\(\dfrac{b}{a} = \dfrac{d}{c}\) D.\(\dfrac{a}{d} = \dfrac{b}{c}\) Câu 4 : Kết quả của phép tính nào sau đây không phải là \({x^{12}}\)? A.\({x^{18}}:{x^6}\) B.\({x^4}.{x^3}\) C.\({x^4}.{x^8}\) D.\({\left[ {{{\left( {{x^3}} \right)}^2}} \right]^2}\) Câu 5 : Kết quả làm tròn số \(0,7126\) đến chữ số thập phân thứ \(3\) là: A.\(0,712\) B.\(0,713\) C.\(0,716\) D.\(0,700\) Câu 6 : Chọn câu trả lời đúng: Cho \(\Delta ABC\), xét các góc trong ta có: A.\(\angle A + \angle B = {180^0}\) B.\(\angle A + \angle B + \angle C = {160^0}\) C.\(\angle A + \angle B + \angle C = {180^0}\) D.\(\angle A + \angle B + \angle {C^0} < {180^0}\) Câu 7 : Cho ba đường thẳng \(a,\,\,b,\,\,c\) phân biệt. Biết \(a \bot c\) và \(b \bot c\) suy ra: A.\(a\) trùng \(b\) B.\(a\)// \(b\) C.\(a\) và \(b\) cắt nhau D.\(a \bot b\) Câu 8 : Đường trung trực của đoạn thẳng \(AB\) là: A. Đường thẳng vuông góc với \(AB\). B. Đường thẳng đi qua trung điểm của\(AB\). C. Đường thẳng vuông góc với \(AB\)tại trung điểm của \(AB\). D. Đường thẳng cắt đoạn thẳng\(AB\). II. Tự luận:(8.0 điểm) Bài 1 (1 điểm):Thực hiện phép tính: \(a)\,\,A = 5.\left| { - \dfrac{1}{{12}}} \right| + \left( {\dfrac{5}{9} - \dfrac{7}{{12}}} \right) - {\left( {\dfrac{2}{3} - \dfrac{5}{6}} \right)^2}\\b)\,\,B = {\left( {\dfrac{3}{5}} \right)^4}.{\left( {\dfrac{5}{3}} \right)^3}\) Bài 2 (1,25 điểm): Tìm \(x\) biết: \(a)\,\,\left| {x + 1} \right| + \dfrac{2}{5} = 1\dfrac{3}{4}:\dfrac{5}{4} + 2\\b)\,\,{3^{x + 2}} - {3^x} = 24\) Bài 3 (1,75 điểm): a) Tìm \(3\) số \(a,\,\,b,\,\,c\) biết \(a,\,\,b,\,\,c\) tỉ lệ nghịch với \(2;\,\,3;\,\,4\) theo thứ tự và \(a + b - c = 21\). b) Các cạnh \(x,\,\,y,\,\,z\) của một tam giác tỉ lệ với \(2;\,\,4;\,\,5\). Tìm độ dài các cạnh của tam giác đó biết tổng độ dài cạnh lớn nhất và cạnh nhỏ nhất hơn độ dài cạnh còn lại là \(20cm\). Câu 4 (3,5 điểm):Cho \(\Delta ABC\) có cạnh \(AB = AC,\,\,M\)là trung điểm của \(BC\). a) Chứng minh\(\Delta ABM = \Delta ACM\). b) Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(MD = MA\). Chứng minh \(AC = BD\). c) Chứng minh \(AB\)//\(CD\). d) Trên nửa mặt phẳng bờ là \(AC\) không chứa điểm \(B\), vẽ tia \(Ax\)//\(BC\), lấy điểm \(I \in Ax\) sao cho \(AI = BC\). Chứng minh \(3\) điểm \(D,\,\,C,\,\,I\) thẳng hàng. Câu 5 (0,5 điểm): Tìm giá trị lớn nhất của biểu thức: \(A = \left| {x - 2018} \right| - \left| {x - 2017} \right|\) Lời giải chi tiết I. Trắc nghiệm
II. TỰ LUẬN: (7 điểm) II. TỰ LUẬN: (7 điểm) Bài 1 : \(\begin{array}{l}a)\,\,A = 5.\left| { - \dfrac{1}{{12}}} \right| + \left( {\dfrac{5}{9} - \dfrac{7}{{12}}} \right) - {\left( {\dfrac{2}{3} - \dfrac{5}{6}} \right)^2}\,\,\,\\\,\,\,\,\,\,\;\;\; = \,\,5.\dfrac{1}{{12}} + \,\,\,\left( {\dfrac{{20}}{{36}} - \dfrac{{21}}{{36}}} \right) - {\left( {\dfrac{4}{6} - \dfrac{5}{6}} \right)^2}\\\,\,\,\,\,\,\;\;\, = \,\,\,\dfrac{5}{{12}} - \dfrac{1}{{36}} - {\left( { - \dfrac{1}{6}} \right)^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\;\; = \,\,\,\dfrac{5}{{12}} - \dfrac{1}{{36}} - \,\dfrac{1}{{36}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\;\, = \,\,\,\dfrac{{15}}{{36}} - \dfrac{1}{{36}} - \,\dfrac{1}{{36}}\,\\\,\,\,\;\,\,\,\; = \dfrac{{15 - 1 - 1}}{{36}} = \dfrac{{13}}{{36}}\,\,\,\,\,\,\,\,\,\end{array}\)\(\begin{array}{l}b)\,\,B = {\left( {\dfrac{3}{5}} \right)^4}.{\left( {\dfrac{5}{3}} \right)^3}\,\\\;\;\;\;\;\;\; = \dfrac{{{3^4}}}{{{5^4}}}.\dfrac{{{5^3}}}{{{3^3}}}\\\;\;\;\;\;\;\; = \dfrac{{{3^4}{{.5}^3}}}{{{5^4}{{.3}^3}}}\\\;\;\;\;\;\;\; = \dfrac{3}{5}.\\\\\\\\\end{array}\) Bài 2 : \(\begin{array}{l}a)\,\,\left| {x + 1} \right| + \dfrac{2}{5} = 1\dfrac{3}{4}:\dfrac{5}{4} + 2\,\\\,\,\,\,\,\,\,\left| {x + 1} \right| + \dfrac{2}{5} = \dfrac{7}{4}:\dfrac{5}{4} + 2\,\\\,\,\,\,\,\,\left| {x + 1} \right| + \dfrac{2}{5} = \dfrac{7}{4} \cdot \dfrac{4}{5} + 2\\\,\,\,\,\,\,\left| {x + 1} \right| + \dfrac{2}{5} = \dfrac{7}{5} + 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\left| {x + 1} \right| = \dfrac{7}{5} + 2\, - \dfrac{2}{5}\\\,\,\,\,\,\,\left| {x + 1} \right| = 3\\\,\,\,\, \Rightarrow \left[ \begin{array}{l}x + 1 = 3\\x + 1 = - 3\end{array} \right.\,\,\,\, \\\Rightarrow \left[ \begin{array}{l}x = 3 - 1\\x = - 3 - 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 4\end{array} \right.\end{array}\) Vậy \(x = 2\) hoặc \(x = - 4\). \(\begin{array}{l}b)\,\,{3^{x + 2}} - {3^x} = 24\\\,\,\,\,\,\,{3^x}{.3^2} - {3^x}.1 = 24\\\,\,\,\,\,{3^x}.({3^2} - 1) = 24\\\,\,\,\,{3^x}.8\;\;\;\;\;\;\;\;\; = 24\\\,\,\,\,{3^x}\;\;\;\;\;\;\;\;\;\;\; = 24:8\\\,\,\,\,{3^x}\;\;\;\;\;\;\;\;\;\;\; = 3\\\,\,\,x\;\;\;\;\;\;\;\;\;\;\;\; = 1\end{array}\) Vậy \(x = 1\). Câu 3 a) Gọi \(3\) số cần tìm là \(a\,,\,\,b\,,\,\,c\). Theo bài ra ta có: \(2a = 3b = 4c\) và \(a + b - c = 21\). Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\begin{array}{l}\dfrac{a}{{\dfrac{1}{2}}} = \dfrac{b}{{\dfrac{1}{3}}} = \dfrac{c}{{\dfrac{1}{4}}} = \dfrac{{a + b - c}}{{\dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4}}} = \dfrac{{21}}{{\dfrac{7}{{12}}}} = 36\\\dfrac{a}{{\dfrac{1}{2}}} = 36\,\, \Rightarrow a = 36.\dfrac{1}{2} = 18;\\\dfrac{b}{{\dfrac{1}{3}}} = 36\,\, \Rightarrow b = 36.\dfrac{1}{3} = 12;\\\dfrac{c}{{\dfrac{1}{4}}} = 36\,\, \Rightarrow c = 36.\dfrac{1}{4} = 9\end{array}\) Vậy các số \(a\,,\,\,b\,,\,\,c\)lần lượt là \(18\,;\,\,12\,;\,\,9.\) b) Gọi \(3\) cạnh của tam giác đó lần lượt là \(x\,;\,\,y\,;\,\,z\,\,\,(cm,\,0 < x < y < z)\). Theo bài ra ta có: \(\dfrac{x}{2} = \dfrac{y}{4} = \dfrac{z}{5}\) và \(x + z - y = 20\). Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\begin{array}{l}\dfrac{x}{2} = \dfrac{y}{4} = \dfrac{z}{5} = \dfrac{{x + z - y}}{{2 + 5 - 4}} = \dfrac{{20}}{3}\\\dfrac{x}{2} = \dfrac{{20}}{3} \Rightarrow x = \dfrac{{40}}{3}\,\,\,(tm)\\\dfrac{y}{4} = \dfrac{{20}}{3} \Rightarrow y = \dfrac{{80}}{3}\,\,\,(tm)\\\dfrac{z}{5} = \dfrac{{20}}{3} \Rightarrow z = \dfrac{{100}}{3}\,\,\,(tm)\end{array}\) Vậy độ dài \(3\) cạnh của tam giác đó lần lượt là: \(\dfrac{{40}}{3}cm\,\,;\,\,\,\dfrac{{80}}{3}cm\,;\,\,\dfrac{{100}}{3}cm\). Câu 4
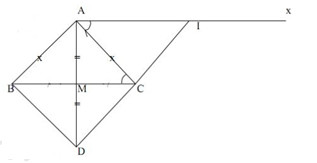
\(AB = AC\,\,(gt)\) \(BM = CM\,\,\) (do \(M\) là trung điểm của \(BC\)) \(AM\) là cạnh chung Vậy \(\Delta ABM = \Delta ACM\,\,(c.c.c)\) b) Xét \(\Delta AMC\) và \(\Delta DMB\) có: \(AM = MD\,\,(gt)\) \(BM = CM\,\,\) (do \(M\) là trung điểm của \(BC\)) \(\angle AMC = \angle DMB\) (hai góc đối đỉnh) Vậy \(\Delta AMC = \Delta DMB\,\,(c.g.c)\) Suy ra \(AC = DB\) (hai cạnh tương ứng) c) Xét \(\Delta AMB\) và \(\Delta DMC\) có: \(AM = MD\,\,(gt)\) \(BM = CM\,\,\) (do \(M\) là trung điểm của \(BC\)) \(\angle AMB = \angle DMC\) (hai góc đối đỉnh) Vậy \(\Delta AMB = \Delta DMC\,\,(c.g.c)\) Suy ra \(\angle ABM = \angle DCM\) (hai góc tương ứng). Mà góc \(ABM\) và góc \(DCM\) là hai góc so le trong Suy ra \(AB\) // \(CD\) (dấu hiệu nhận biết hai đường thẳng song song) d) Xét \(\Delta AIC\) và \(\Delta CBA\) có: \(AI = BC\,\,(gt)\) \(\angle IAC = \angle BCA\) (hai góc so le trong,) \(AC\) là cạnh chung Vậy \(\Delta AIC = \Delta CBA\,\,(c.g.c)\) Suy ra \(\angle ACI = \angle CAB\) (hai góc tương ứng). Mà góc \(ACI\) và góc \(CAB\) là hai góc so le trong Suy ra \(AB//CI\) (dấu hiệu nhận biết hai đường thẳng song song) Lại có \(AB//CD\) (theo chứng minh câu c). Theo tiên đề Ơ-clit thì đường thẳng \(CD\) trùng với đường thẳng \(CI\). Do đó ba điểm \(D,C,I\) thẳng hàng. Câu 5 Áp dụng bất đẳng thức \(\left| {a - b} \right| \ge \left| a \right| - \left| b \right|\) ta có: \(A = \left| {x - 2017} \right| - \left| {x - 2018} \right| \le \left| {(x - 2017) - (x - 2018)} \right| = \left| 1 \right| = 1\) Dấu “=” xảy ra \(\left\{ \begin{array}{l}\left( {x - 2018} \right)\left( {x - 2017} \right) \ge 0\\x - 2018 \le x - 2017\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 2018\\x \le 2017\end{array} \right..\) Vậy giá trị lớn nhất của \(A\) là \(1\). Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 7 tại HocTot.Nam.Name.Vn HocTot.Nam.Name.Vn
|
||||||||||||||