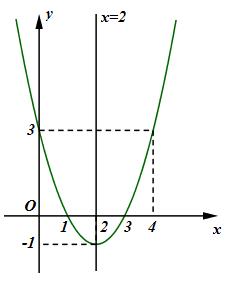Đề số 8 – Đề kiểm tra học kì 1 – Toán 10

Đề bài

A. PHẦN TRẮC NGHIỆM: (4 điểm)

Câu 1 : Cho hình bình hành \(ABCD\). Trong các khẳng định sau hãy tìm khẳng định sai ?

A. \(\overrightarrow {AB}  = \overrightarrow {DC} \).

B. \(\left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\).

C. \(\overrightarrow {AD}  = \overrightarrow {CB} \).

D. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\).

Câu 2 : Tìm tọa độ đỉnh parabol \(y =  - 2{x^2} + 4x - 2\).

A. \(I\left( {1;1} \right)\).     B. \(I\left( { - 2;2} \right)\).

C. \(I\left( {1;0} \right)\).     D. \(I\left( {2;2} \right)\).

Câu 3 : Trong mặt phẳng tọa độ Oxy cho hai vectơ \(\overrightarrow a  = (1;2),\,\overrightarrow {\,\,\,b}  = ( - 3;5).\,\)Tìm tọa độ của vectơ \(\overrightarrow u  = \overrightarrow a  - \overrightarrow b .\)

A. \(\overrightarrow u  = ( - 4;3).\)

B. \(\overrightarrow u  = ( - 2;7).\)

C. \(\overrightarrow u  = ( - 3;5).\)

D. \(\overrightarrow u  = (4; - 3).\)

Câu 4 : Trong mặt phẳng Oxy, cho \(A(2; - 3),{\rm{ }}B(0;1)\). Tìm tọa độ của vectơ \(\overrightarrow {AB} \).

A. \(\overrightarrow {AB}  = \left( {4;2} \right)\).

B. \(\overrightarrow {AB}  = \left( {2; - 4} \right)\).

C. \(\overrightarrow {AB}  = \left( { - 2;4} \right)\).

D. \(\overrightarrow {AB}  = \left( { - 2; - 4} \right)\).

Câu 5 : Trong mặt phẳng Oxy, cho \(A(1; - 1),{\rm{ }}B(2; - 3)\). Tìm tọa độ điểm \(D\) sao cho \(\overrightarrow {AD}  = 3\overrightarrow {AB} .\)

A. \(D(4; - 7)\).                     B. \(D( - 4; - 1)\).

C. \(D(4; - 1)\).                     D. \(D( - 4;1).\)

Câu 6 : Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?

A. \(\overrightarrow {AC}  = \overrightarrow {BD} \).

B. \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \).

C. \(\overrightarrow {AB}  = \overrightarrow {CD} \).

D. \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \).

Câu 7 : Trong mặt phẳng Oxy, cho \(A(4; - 3),{\rm{ }}B(2; - 1)\). Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(AB\).

A. \(I\left( {2; - 2} \right)\).  B. \(I\left( {6; - 4} \right)\).

C. \(I\left( { - 2;2} \right)\).  D. \(I\left( {3; - 2} \right)\).

Câu 8 : Cho tập hợp \(A = \left\{ {1;2;4;5} \right\};\,\,B = \left\{ {2;4;6} \right\}\). Xác định tập hợp \(A \cup B\).

A. \(\left\{ {1;2;4;5;6} \right\}\). 

B. \(\left\{ {1;5} \right\}\)

C. \(\left\{ {1;2;3;4;5;6} \right\}\). 

D. \(\left\{ {2;4} \right\}\).

Câu 9 : Tìm tập xác định của hàm số \(y = \sqrt {3x + 6} \).

A. \(\left( { - \infty ; - 2} \right]\).

B. \(\left[ { - 2; + \infty } \right)\).

C. \(\left[ {2; + \infty } \right)\).

D. \(\left( { - 2; + \infty } \right)\).

Câu 10 : Cho \(\left( P \right):y =  - {x^2} + 2x + 3\). Chọn khẳng định đúng ?.

A. Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).

B. Hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;1} \right)\).

C. Hàm số đồng biến trên \(\left( { - 1; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - 1} \right)\).

D. Hàm số đồng biến trên \(\left( { - \infty ; - 1} \right)\)và nghịch biến trên\(\left( { - 1; + \infty } \right)\).

Câu 11 : Hàm số nào sau đây là hàm số chẵn ?

A. \(y = {x^4}\)

B. \(y = {x^4} + 1\).

C. \(y = {x^3}\).

D. \(y = {x^3} + 1.\)

Câu 12 : Cho tập hợp \(A = \left[ { - 2;5} \right);\,\,B = \left( {2;10} \right)\). Xác định tập hợp \(A \cap B\).

A. \(\left[ { - 2;2} \right)\).   B. \(\left( {2;5} \right)\).

C. \(\left( {5;10} \right)\).    D. \(\left[ { - 2;10} \right)\).

Câu 13 : Cho tập hợp \(A = \left\{ {x \in Z|\left( {x + 4} \right)\left( {{x^2} - 3x + 2} \right) = 0} \right\}\). Viết tập hợp \(A\) bằng cách liệt kê phần tử.

A. \(A = \left\{ {1;2;4} \right\}\).

B. \(A = \left\{ { - 1;2;3} \right\}\).

C. \(A = \left\{ {1;2; - 4} \right\}\).

D. \(A = \left\{ {1;2;3} \right\}\).

Câu 14 : Tìm tập  nghiệm của phương trình \(\sqrt {{x^2} - x - 2}  = \sqrt {x - 2} \).

A. \(S = \left\{ { - 1;2} \right\}\).

B. \(S = \left\{ 0 \right\}.\)

C. \(S = \left\{ 2 \right\}\).

D. \(S = \left\{ {0;2} \right\}\).

Câu 15 : Tìm tập  nghiệm của phương trình \(\sqrt {x - 5}  = 2\).

A. \(S = \left\{ 3 \right\}\).   B. \(S = \left\{ 9 \right\}\).

C. \(S = \emptyset \).            D. \(S = \left\{ 7 \right\}\).

Câu 16 : Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Hỏi \(\overrightarrow {BM}  + \overrightarrow {MP} \) bằng vectơ nào?

A. \(\overrightarrow {MN} \) .                                     B. \(\overrightarrow {BA} \).

C. \(\overrightarrow {BC} \).                                       D. \(\overrightarrow {AP} \).

Câu 17 : Tìm trục đối xứng của parabol \(y = 2{x^2} + 4x - 1\).

A. \(x = 1\).                           B. \(x = 2\).

C. \(x =  - 2\).                       D. \(x =  - 1\) .

Câu 18 : Tìm nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y - 3 = 0\\x - 3y + 1 = 0\end{array} \right.\).

A. \(( - 2; - 1)\)                      B. \((3;1)\).

C. \((2;3)\).                           D. \((2;1)\).

Câu 19 : Tìm a để đường thẳng \(y = ax - 1\) đi qua điểm \(M\left( {1;3} \right)\).

A. \(a = 2\).                           B. \(a = 4\).

C. \(a = 1\).                           D. \(a = 0\).

Câu 20 : Điểm nào dưới đây thuộc đồ thị hàm số \(y = 3x - 1\).

A. \((1;1)\).                           B. \((2;5)\).

C. \((2;3)\).                           D. \((0;1)\)

B. PHẦN TỰ LUẬN: (6 điểm)

Bài 1 . (2.0 điểm) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\)

Bài 2 . (1.0 điểm) Giải phương trình \(\sqrt {x - 1}  = x - 3\)

Bài 3 . (2.0 điểm) Trong mp Oxy, cho ba điểm \(A\left( {1;1} \right);\,\,B\left( {3;2} \right);\,\,C\left( {4; - 1} \right)\).

             a) Tìm tọa độ điểm \(D\) sao cho \(ABCD\) là hình bình hành.

             b) Tìm tọa độ điểm \(M\) thỏa mãn \(\overrightarrow {AM}  = 2\overrightarrow {AB}  - \overrightarrow {BC} \).

Bài 4 . (1.0 điểm) Xác định \(m\) để phương trình \({x^2} + 1 = mx\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa \({x_1} - {x_2} = 1\) (giả sử \({x_1} > {x_2}\)).

Lời giải chi tiết

A. PHẦN TRẮC NGHIỆM

1. C	2. C	3. D	4. C	5. A
6. D	7. D	8. A	9. B	10. A
11. A	12.B	13.C	14.C	15. B
16. A	17.D	18.D	19.B	20. B

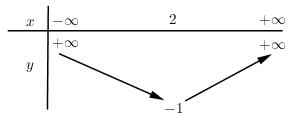
B. PHẦN TỰ LUẬN: (6 điểm)

Bài 1:

+) TXĐ: \(D = R\).

+) Tọa độ đỉnh \(I\left( {2; - 1} \right)\)

+) Trục đối xứng \(x = 2\)

+) Tính biến thiên:

     Hàm số đồng biến trên \(\left( {2; + \infty } \right)\)

     Hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\).

+) Bảng biến thiên:

 

+) Đồ thị:

    Giao Ox: Cho \(y = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)

    Giao Oy: Cho \(x = 0 \Rightarrow y = 3\)

 

Bài 2:

\(\begin{array}{l}\sqrt {x - 1}  = x - 3\\ \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\x - 1 = {\left( {x - 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x - 1 = {x^2} - 6x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} - 7x + 10 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 5\\x = 2\end{array} \right.\end{array} \right. \Leftrightarrow x = 5\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ 5 \right\}\).

Bài 3:

a) Để ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {DC} \)

\(\begin{array}{l} \Leftrightarrow \left( {2;1} \right) = \left( {4 - {x_D}; - 1 - {y_D}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2 = 4 - {x_D}\\1 =  - 1 - {y_D}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2\\{y_D} =  - 2\end{array} \right.\\ \Rightarrow D\left( {2; - 2} \right)\end{array}\)

Vậy \(D\left( {2; - 2} \right)\).

b) Ta có \(\overrightarrow {AB}  = \left( {2;1} \right);\,\,\overrightarrow {BC}  = \left( {1; - 3} \right) \\\Rightarrow 2\overrightarrow {AB}  - \overrightarrow {BC}  = \left( {3;5} \right)\)

\(\begin{array}{l} \Rightarrow \overrightarrow {AM}  = \left( {3;5} \right) \\\Rightarrow \left( {{x_M} - 1;{y_M} - 1} \right) = \left( {3;5} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}{x_M} - 1 = 3\\{y_M} - 1 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 4\\{y_M} = 6\end{array} \right. \\ \Rightarrow M\left( {4;6} \right)\end{array}\).

Vậy \(M\left( {4;6} \right)\).

Bài 4:

\({x^2} + 1 = mx \Leftrightarrow {x^2} - mx + 1 = 0\)

Để phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta  = {m^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\\m <  - 2\end{array} \right.\)

Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = 1\end{array} \right.\)

Ta có:

\(\begin{array}{l}{x_1} - {x_2} = 1 \\\Rightarrow {\left( {{x_1} - {x_2}} \right)^2} = 1\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 1\\ \Leftrightarrow {m^2} - 4 = 1 \Leftrightarrow {m^2} = 5 \\\Leftrightarrow m =  \pm \sqrt 5 \,\,\left( {tm} \right)\end{array}\)

Vậy \(m =  \pm \sqrt 5 \).

Xem lời giải chi tiết đề thi học kì 1 tại HocTot.Nam.Name.Vn

HocTot.Nam.Name.Vn