Đề số 5 - Đề kiểm tra học kì 1 - Toán 8

Đề bài

Bài 3 (2,5 điểm)

1. Cho biểu thức: $P = \dfrac{{{a^2} - 1}}{{{a^2} - a}}$ . Rút gọn rồi tính giá trị của biểu thức $P$ tại $a =  - 2$.
2. Với $x \ne  \pm 2$ chứng minh đẳng thức:

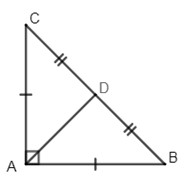
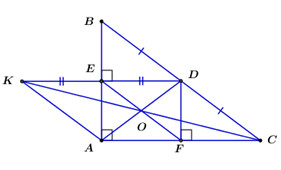
$\left( {\dfrac{x}{{2 + x}} - \dfrac{1}{{x - 2}} - \dfrac{{x + 3}}{{4 - {x^2}}}} \right):\left( {\dfrac{{{x^2} - 3}}{{4 - {x^2}}} + 1} \right) =  - {\left( {x - 1} \right)^2}$

Bài 4 (1,5 điểm)Cho $\Delta ABC$ vuông tại $A$ , có $D$ là trung điểm của $BC$. Gọi $E,\,F$ lần lượt là hình chiếu của $D$  trên $AB$  và $AC$.

1. Chứng minh: $A{\rm{D}} = EF$
2. Gọi K là điểm đối xứng với $D$  qua $E$. Chứng minh ba đường thẳng $A{\rm{D}},\,EF,\,KC$đồngquy.

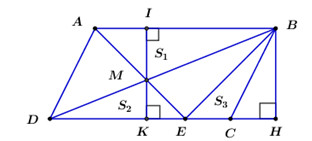
Bài 5  (1 điểm)

1. Cho hình bình hành $ABC{\rm{D}}$, điểm $E$ nằm giữa hai điểm $C$  và $D$. Gọi $M$ là giao điểm của $A{\rm{E}}$  và $B{\rm{D}}$. Gọi diện tích$ABM$ là ${S_1}$, diện tích$\Delta MDE$  là ${S_2}$, diện tích $\Delta BCE$ là ${S_3}$. So sánh ${S_1}$ với ${S_2} + {S_3}.$
2. Cho $x,\,y$ là hai số thực thỏa mãn:${x^2} + {y^2} = 1$. Tìm giá trị lớn nhất của biểu thức: $M = {x^5} + 2y.$

LG bài 1

Lời giải chi tiết:

Bài 1.

1.Chọn D

2.Chọn C

3.

Cho $\Delta ABC$ vuông cân tại $A$, có $A{\rm{D}}$ là đường trung tuyến, $A{\rm{D}} = \sqrt 2 \,cm$.

Vì $\Delta ABC$ vuông cân tại $A$, có $A{\rm{D}}$ là đường trung tuyến (gt)

$\Rightarrow BC = 2{\rm{AD}} = 2\sqrt 2 \,cm$ (trong tam giác vuông đường trung

tuyến ứng với cạnh huyền bằng nửa cạnh ấy)

Áp dụng định lý Py-ta-go có:

$\begin{array}{l}A{B^2} + A{C^2} = B{C^2} \Rightarrow 2{\rm{A}}{B^2} = B{C^2}\\ \Rightarrow A{B^2} = {\left( {2\sqrt 2 } \right)^2}:2 = 4\, \Rightarrow AB = AC = 2\,cm.\end{array}$

4.Chọn B.

LG bài 2

Lời giải chi tiết:

1. Ta có:

$\begin{array}{l}a)\;\;3{x^2} - 6x + 2xy - 4y = 3x\left( {x - 2} \right) + 2y\left( {x - 2} \right) = \left( {x - 2} \right)\left( {3x + 2y} \right).\\b)\;\;{a^2}\left( {{a^2} + 4} \right) - {a^2} + 4 = {a^4} + 4{a^2} - {a^2} + 4\\ = \left( {{a^4} + 4{a^2} + 4} \right) - {a^2} = {\left( {{a^2} + 2} \right)^2} - {a^2}\\ = \left( {{a^2} + 2 - a} \right)\left( {{a^2} + 2 + a} \right).\end{array}$

$\begin{array}{l}2.\;{x^2} - x + 0,25 = 0 \Leftrightarrow {x^2} - x + \dfrac{1}{4} = 0\\ \Leftrightarrow 4{x^2} - 4x + 1 = 0 \Leftrightarrow {\left( {2x - 1} \right)^2} = 0\\ \Leftrightarrow 2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2}.\end{array}$

Vậy $x = \dfrac{1}{2}.$

LG bài 3

Lời giải chi tiết:

1. Phân thức xác định khi và chỉ khi${a^2} - a \ne 0 \Leftrightarrow a\left( {a - 1} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\a - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\a \ne 1\end{array} \right.$

$P = \dfrac{{{a^2} - 1}}{{{a^2} - a}} = \dfrac{{\left( {a - 1} \right)\left( {a + 1} \right)}}{{a\left( {a - 1} \right)}} = \dfrac{{a + 1}}{a}.$

Thay $a =  - 2$ vào biểu thức $P$ ta được: $P = \dfrac{{a + 1}}{a} = \dfrac{{ - 2 + 1}}{{ - 2}} = \dfrac{1}{2}.$

1. $\left( {\dfrac{x}{{2 + x}} - \dfrac{1}{{x - 2}} - \dfrac{{x + 3}}{{4 - {x^2}}}} \right):\left( {\dfrac{{{x^2} - 3}}{{4 - {x^2}}} + 1} \right) = {\left( {x - 1} \right)^2}\,\,\left( {x \ne  \pm 2} \right)$

Biến đổi vế trái của đẳng thức ta có:

$\begin{array}{l}\left( {\dfrac{x}{{2 + x}} - \dfrac{1}{{x - 2}} - \dfrac{{x + 3}}{{4 - {x^2}}}} \right):\left( {\dfrac{{{x^2} - 3}}{{4 - {x^2}}} + 1} \right) \\= \left( {\dfrac{x}{{2 + x}} + \dfrac{1}{{2 - x}} - \dfrac{{x + 3}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}} \right):\left( {\dfrac{{{x^2} - 3 + 4 - {x^2}}}{{4 - {x^2}}}} \right)\\ = \dfrac{{x\left( {2 - x} \right) + \left( {x + 2} \right) - x - 3}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}:\dfrac{1}{{4 - {x^2}}}\\ = \dfrac{{2x - {x^2} + x + 2 - x - 3}}{{4 - {x^2}}}.\left( {4 - {x^2}} \right)\\ =  - {x^2} + 2x - 1 =  - {\left( {x - 1} \right)^2}\end{array}$

1. Ta có:

$\begin{array}{l}A = {\left( {m - 1} \right)^3} - \left( {{m^2} + 1} \right)\left( {m - 3} \right) - 2m\\ = {m^3} - 3{m^2} + 3m - 1 - \left( {{m^3} - 3{m^2} + m - 3} \right) - 2m\\ = {m^3} - 3{m^2} + m - 1 - {m^3} + 3{m^2} - m + 3\\ = 2.\end{array}$

Vì $2$ là số nguyên tố nên ${\left( {m - 1} \right)^3} - \left( {{m^2} + 1} \right)\left( {m - 3} \right) - 2m$ là số nguyên tố với mọi $m.$

LG bài 4

Lời giải chi tiết:

1. Xét tứ giác $A{\rm{ED}}F$ có: $\angle BAC = \angle A{\rm{ED}} = \angle AFD = {90^0}\left( {gt} \right) \Rightarrow A{\rm{ED}}F$ là hình chữ nhật (dhnb)

$\Rightarrow A{\rm{D}} = EF$ (tính chất hình chữ nhật)

1. Gọi $O$ là giao điểm của $EF$ và $A{\rm{D}} \Rightarrow {\rm{O}}$là trung điểm của $EF$ và $A{\rm{D}}$(tính chất hình chữ nhật) (1)

$\Rightarrow OE = OF$ (tính chất trung điểm)

Do D và K đối xứng nhau qua E nên suy ra $\left\{ \begin{array}{l}DK \bot AB\\ED = KE\end{array} \right.$ (tính chất đối xứng)

Mà $AC \bot AB\left( {gt} \right) \Rightarrow DK//AC$ (từ vuông góc đến song song)

Ta có: $ED$ là đường trung bình của $\Delta ABC$ (E, D là

trung điểm của AB, BC (gt))

$\Rightarrow ED = \dfrac{1}{2}BC \Rightarrow BC = 2ED.$

Xét tứ giác $AKDC$ ta có:

$\begin{array}{l}AC//KD\;\;\left( {cmt} \right)\\KD = AC\;\;\left( { = 2ED} \right)\end{array}$

$\Rightarrow AKDC$ là hình bình hành (dhnb)

$\Rightarrow KC,\;EF$ cắt nhau tại trung điểm của mỗi đường (tính chất)

Mà O là trung điểm của EF  (cách gọi)

$\Rightarrow KC,\;\;EF,\;\;AD$ đồng quy tại $O.$ (đpcm)

LG bài 5

Lời giải chi tiết:

1. Kẻ $IK \bot AB;\;\;BH \bot CD$ như hình vẽ. Ta có:

$\begin{array}{l}{S_1} = {S_{ABM}} = \dfrac{1}{2}MI.AB\\{S_2} = {S_{MDE}} = \dfrac{1}{2}MK.DE\\{S_3} = {S_{BEC}} = \dfrac{1}{2}BH.EC\end{array}$

$\begin{array}{l} \Rightarrow {S_2} + {S_3} = \dfrac{1}{2}MK.DE + \dfrac{1}{2}BH.EC\\ = \dfrac{1}{2}\left[ {MK.DE + \left( {MI + MK} \right).EC} \right]\\ = \dfrac{1}{2}\left( {MK.DE + MK.EC + MI.EC} \right)\\ = \dfrac{1}{2}\left( {MK.DC + MI.EC} \right)\end{array}$

2. Ta có: ${x^2} + {y^2} = 1 \Rightarrow 0 \le {x^2} \le 1 \Rightarrow  - 1 \le x \le 1 \Rightarrow {x^4} \le {x^2}$

-          TH1: Nếu $x \ge 0 \Rightarrow 0 \le x \le 1 \Rightarrow {x^5} \le {x^2}$

-          TH2: Nếu $x < 0 \Rightarrow {x^5} < {x^2}$

Khi $x < 0 \Rightarrow \left\{ \begin{array}{l}{x^5} < 0\\{x^2} > 0\end{array} \right. \Rightarrow {x^5} < {x^2}$

Do đó ${x^5} \le {x^2}\,\;khi\;\,x \in \left( { - 1;\,1} \right)$(1)

Ta có: ${\left( {y - 1} \right)^2} \ge 0 \Rightarrow {y^2} - 2y + 1 \ge 0 \Rightarrow {y^2} + 1 \ge 2y$ (2)

Cộng vế với vế của (1) và (2) ta được:

$\begin{array}{l}{x^5} + 2y \le {x^2} + {y^2} + 1\\ \Leftrightarrow {x^5} + 2y \le 2\end{array}$

Dấu “=” xảy ra khi và chỉ khi$y - 1 = 0 \Leftrightarrow y = 1 \Rightarrow x = 0.$

Vậy $Max\,\left( {{x^5} + 2y} \right) = 2\;\;\,khi\;\;\,\left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.$.

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại HocTot.Nam.Name.Vn

 HocTot.Nam.Name.Vn