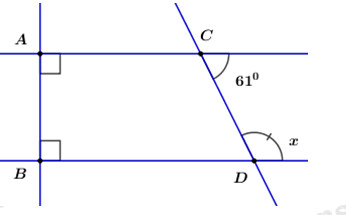
Đề số 4 - Đề kiểm tra học kì 1 - Toán 7Đáp án và lời giải chi tiết Đề số 4 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 7 Đề bài Phần I – Trắc nghiệm (2,0 điểm) Hãy viết chữ cái in hoa đứng trước phương án đúng trong mỗi câu sau vào bài làm. Câu 1 :Cho biết x và y là hai đại lượng tỉ lệ thuận, biết khi x = 5 thì y = 15. Hệ số tỉ lệ của y đối với x là: A.\(\dfrac{1}{3}\). B.3. C.75. D.10. Câu 2 : Kết quả phép tính \({\left( { - 2017} \right)^0} + \sqrt {121} - 2\sqrt 9 \) là: A.6. B.– 2012. C.– 6. D.– 2024. Câu 3 : Kết quả của phép tính \({\left( {\dfrac{9}{4}} \right)^3}:{\left( {\dfrac{3}{2}} \right)^4}\)bằng: A.\(\dfrac{3}{2}\). B.\(\dfrac{4}{9}\). C.\(\dfrac{2}{3}\). D.\(\dfrac{9}{4}\). Câu 4 : Cho a, b, c, d là các số thực khác không (\(a \ne b;\;c \ne d\)), từ tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\) có thể suy ra kết quả nào sau đây: A.\(\dfrac{{a - b}}{b} = \dfrac{d}{{c - d}}\). B.\(\dfrac{{a + b}}{a} = \dfrac{{c + d}}{c}\). C.\(ac = b{\rm{d}}\). D.\(ab = c{\rm{d}}\). Câu 5 : Nếu tam giác ABC vuông tại A thì: A.\(\angle B + \angle C > {90^0}\) B.\(\angle B + \angle C < {90^0}\) C.\(\angle B + \angle C = {90^0}\) D.\(\angle B + \angle C = {180^0}\) Câu 6 : Một mảnh đất hình chữ nhật có độ dài hai cạnh tỉ lệ với các số 1 và 4, biết chu vi mảnh đất là 50m thì diện tích của mảnh đất đó là: A.100. B.25. C.20. D.5. Câu 7 : Trên hình vẽ, tính số đo x ta được: A.610 B.1290 C.1190 D.290
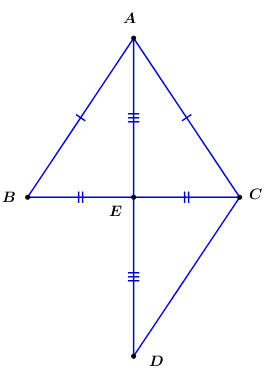
Câu 8 : Nếu \(c \bot a\) và b //a thì: A.a // b. B.b // c. C.\(a \bot b\). D.\(c \bot b\). Phần II – Tự luận (8,0 điểm) Câu 9 (2,5 điểm).Thực hiện phép tính: a) \(\dfrac{4}{3} - \dfrac{2}{5}\) b) \(\left| {\dfrac{{ - 1}}{{10}}} \right| - {\left( {\dfrac{1}{3}} \right)^2}:\dfrac{5}{9}\) c) \(7,5:\left( {\dfrac{{ - 5}}{4}} \right) + 2\dfrac{1}{2}:\left( {\dfrac{{ - 5}}{4}} \right)\) d) \({\left( { - 0,2} \right)^2}.5 - \dfrac{{{8^2}{{.9}^4}}}{{{3^7}{{.4}^3}}}\) Câu 10 (1,0 điểm).Tìm x biết: a) \(x + \dfrac{2}{3} = - \dfrac{1}{{12}}\) b) \({\left( {2{\rm{x}} + 1} \right)^2} = 9\) Câu 11 (1,0 điểm). Trong đợt thi đua hái hoa điểm tốt lập thành tích chào mừng kỉ niệm 35 năm ngày Nhà giáo Việt Nam (20/11/1982 – 20/11/2017), tỉ số bông hoa điểm tốt của lớp 7A và lớp 7B là \(\dfrac{5}{6}\), đồng thời số bông hoa điểm tốt của lớp 7A ít hơn lớp là 10 bông. Tính số bông hoa điểm tốt mỗi lớp đã hái được? Câu 12 (3,0 điểm). Cho tam giác ABC có AB = AC, E là trung điểm BC, trên tia đối của tia EA lấy điểm D sao cho AE = ED. a) Chứng minh: \(\Delta ABE = \Delta DCE\). b) Chứng minh: \(AB//DC\). c) Chứng minh: \(A{\rm{E}} \bot BC\). d) Tìm điều kiện của \(\Delta ABC\) để \(\angle A{\rm{D}}C = {45^0}\). Câu 13 (0,5 điểm). Cho a, b, c là các số thực khác không (\(b \ne c\)) và \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\). Chứng minh rằng: \(\dfrac{a}{b} = \dfrac{{a - c}}{{c - b}}\). Lời giải chi tiết Phần I – Trắc nghiệm (2,0 điểm)
Câu 9: \(\begin{array}{l}a)\;\;\dfrac{4}{3} - \dfrac{2}{5} = \dfrac{{4.5}}{{3.5}} - \dfrac{{2.3}}{{5.3}}\\\;\; = \dfrac{{4.5 - 2.3}}{{3.5}}\\\;\; = \dfrac{{20 - 6}}{{15}} = \dfrac{{14}}{{15}}.\end{array}\) \(\begin{array}{l}c)\;\;7,5:\left( {\dfrac{{ - 5}}{4}} \right) + 2\dfrac{1}{2}:\left( {\dfrac{{ - 5}}{4}} \right)\\\;\;\; = \left( {7,5 + 2\dfrac{1}{2}} \right):\left( {\dfrac{{ - 5}}{4}} \right)\\\;\;\; = \left( {7,5 + \dfrac{5}{2}} \right).\left( {\dfrac{4}{{ - 5}}} \right)\\\;\;\; = \left( {7,5 + 2,5} \right).\left( {\dfrac{4}{{ - 5}}} \right)\\\;\;\; = 10.\left( {\dfrac{4}{{ - 5}}} \right) = - 8.\end{array}\) \(\begin{array}{l}b)\;\left| {\dfrac{{ - 1}}{{10}}} \right| - {\left( {\dfrac{1}{3}} \right)^2}:\dfrac{5}{9} = \dfrac{1}{{10}} - \dfrac{1}{9}.\dfrac{9}{5}\\\;\; = \dfrac{1}{{10}} - \dfrac{1}{5} = \dfrac{1}{{10}} - \dfrac{{1.2}}{{5.2}}\\\;\; = \dfrac{{1 - 2}}{{10}} = \dfrac{{ - 1}}{{10}}.\end{array}\)\(\begin{array}{l}d)\;{\left( { - 0,2} \right)^2}.5 - \dfrac{{{8^2}{{.9}^4}}}{{{3^7}{{.4}^3}}}\\\;\; = {\left( {\dfrac{{ - 1}}{5}} \right)^2}.5 - \dfrac{{{{\left( {{2^3}} \right)}^2}.{{\left( {{3^2}} \right)}^4}}}{{{3^7}.{{\left( {{2^2}} \right)}^3}}}\\\;\; = \dfrac{1}{5} - \dfrac{{{2^6}{{.3}^8}}}{{{3^7}{{.2}^6}}} = \dfrac{1}{5} - {2^{(6 - 6)}}{.3^{(8 - 7)}}\\\;\; = \dfrac{1}{5} - {2^0}{.3^1} = \dfrac{1}{5} - 3\\\;\; = \dfrac{1}{5} - \dfrac{{3.5}}{5}\\\;\; = \dfrac{{1 - 15}}{5} = \dfrac{{ - 14}}{5}.\end{array}\) Câu 10: \(\begin{array}{l}a)\;\;x + \dfrac{2}{3} = - \dfrac{1}{{12}}\\ \Leftrightarrow x\;\;\;\;\;\; = - \dfrac{1}{{12}} - \dfrac{2}{3}\\ \Leftrightarrow x\;\;\;\;\;\; = - \dfrac{1}{{12}} - \dfrac{{2.4}}{{3.4}}\\ \Leftrightarrow x\;\;\;\;\;\; = \dfrac{{ - 1 - 8}}{{12}}\\ \Leftrightarrow x\;\;\;\;\;\; = \dfrac{{ - 9}}{{12}} = \dfrac{{ - 3}}{4}\end{array}\) Vậy x = \(\dfrac{{ - 3}}{4}\). \(\begin{array}{l}b)\;{\left( {2{\rm{x}} + 1} \right)^2} = 9\\ \Leftrightarrow {\left( {2{\rm{x + 1}}} \right)^2} = {3^2}\\ \Rightarrow \left[ \begin{array}{l}2{\rm{x}} + 1 = 3\\2{\rm{x}} + 1 = - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{3 - 1}}{2} = 1\\x = \dfrac{{ - 3 - 1}}{2} = - 2\end{array} \right.\end{array}\) Vậy x = 1 hoặc x = \( - 2\). Câu 11: Gọi số bông hoa điểm tốt của lớp 7A và 7B lần lượt là x và y (bông) \(\left( {x > 0,\;y > 10,\;x,\;y \in N} \right).\) Tỉ số số bông hoa điểm tốt của lớp 7A và 7B là \(\dfrac{5}{6}\). \( \Rightarrow \dfrac{x}{y} = \dfrac{5}{6} \Leftrightarrow \dfrac{x}{5} = \dfrac{y}{6}.\) Số bông hoa điểm tốt của lớp 7A ít hơn lớp 7B là 10 bông, nên: \(y - x = 10.\) Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\begin{array}{l}\dfrac{x}{5} = \dfrac{y}{6} = \dfrac{{y - x}}{{6 - 5}} = \dfrac{{10}}{1} = 10.\\ \Rightarrow \left\{ \begin{array}{l}x = 5.10 = 50\;\;\left( {tm} \right)\\y = 6.10 = 60\;\;\left( {tm} \right)\end{array} \right..\end{array}\) Vậy số bông hoa điểm tốt lớp 7A hái được là 50 bông; số bông hoa điểm tốt lớp 7B hái được là 60 bông. Câu 12:
a) Xét tam giác ABE và tam giác DCE có: BE = EC (E là trung điểm của BC) AE = ED (Theo giả thiết) \(\angle BE{\rm{A}} = \angle CE{\rm{D}}\) (2 góc đối đỉnh) \( \Rightarrow \Delta ABE = \Delta DCE\;\;(c - g - c)\) (đpcm) b) Vì \(\Delta ABE = \Delta DCE\) nên \(\angle EBA = \angle EC{\rm{D}}\) (2 góc tương ứng) Mà \(\angle EBA\) và \(\angle EC{\rm{D}}\) lại là cặp góc ở vị trí so le trong. \( \Rightarrow AB\parallel C{\rm{D}}\) (đpcm) c) Xét tam giác ABC có: AB = AC Suy ra tam giác ABC là tam giác cân tại A. Lại có E là trung điểm của BC \( \Rightarrow AE\) là đường trung tuyến của tam giác ABC cân tại A. \( \Rightarrow AE\) cũng là đường cao của tam giác ABC cân tại A. \( \Rightarrow A{\rm{E}} \bot BC\) (đpcm) d) Vì \(\Delta ABE = \Delta DCE\) nên \(\angle E{\rm{D}}C = \angle E{\rm{A}}B\) (cặp góc tương ứng) \( \Rightarrow \angle A{\rm{D}}C = \angle E{\rm{AB}}\) (1)\(\) Mà AE là đường phân giác của tam giác ABC cân tại A. \(\) \( \Rightarrow \angle E{\rm{A}}B = \angle E{\rm{A}}C\) (2) Từ (1) và (2) ta có: \(\angle A{\rm{D}}C = \angle E{\rm{AB = }}\angle {\rm{EA}}C\) Để \(\angle A{\rm{D}}C\) = 450 thì \(\angle E{\rm{AB }}\) và \(\angle {\rm{EA}}C\) phải bằng 450. Khi đó: \(\angle BAC = \angle BA{\rm{E + }}\angle {\rm{EA}}C = {45^0} + {45^0} = {90^0}\) Vậy để \(\angle A{\rm{D}}C\) = 450 thì \(\angle BAC\)= 900. Suy ra để \(\angle A{\rm{D}}C\) = 450 thì tam giác ABC phải vuông cân tại A. Câu 13: Theo bài ta có: \(\begin{array}{l}\;\;\;\;\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) \Leftrightarrow \dfrac{2}{c} = \dfrac{1}{a} + \dfrac{1}{b}\\ \Leftrightarrow \dfrac{1}{c} + \dfrac{1}{c} = \dfrac{1}{a} + \dfrac{1}{b} \Leftrightarrow \dfrac{1}{c} - \dfrac{1}{a} = \dfrac{1}{b} - \dfrac{1}{c}\\ \Leftrightarrow \dfrac{a}{{c.a}} - \dfrac{c}{{a.c}} = \dfrac{c}{{b.c}} - \dfrac{b}{{c.b}}\\ \Leftrightarrow \dfrac{{a - c}}{{ac}} = \dfrac{{c - b}}{{bc}}\end{array}\) \( \Leftrightarrow \dfrac{{a - c}}{{c - b}} = \dfrac{{ac}}{{bc}} = \dfrac{a}{b}\) (điều phải chứng minh) (Theo tính chất tỉ lệ thức) Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 7 tại HocTot.Nam.Name.Vn HocTot.Nam.Name.Vn
|