Đề số 3 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10

Đề bài

I. TRẮC NGHIỆM (2,0 điểm) Chọn đáp án đúng trong mỗi câu sau:

Câu 1 (NB): Tập nghiệm của bất phương trình \( - {x^2} - 4x + 5 \ge 0\) là

A. \(S = \left( { - \infty ; - 1} \right] \cup \left[ {5; + \infty } \right).\)

B. \(S = \left[ { - 1;5} \right].\)

C. \(S = \left[ { - 5;1} \right]\)

D. \(S = \left( { - 5;1} \right).\)

Câu 2 (NB): Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 1 \ge 0\\4 - 3x \ge 0\end{array} \right.\) là

A. \(S = \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {\frac{4}{3}; + \infty } \right).\)

B. \(S = \left[ {\frac{1}{2};\frac{4}{3}} \right].\)

C. \(S = \left( {\frac{1}{2};\frac{4}{3}} \right).\)

D. \(S = \left[ {\frac{1}{2};\frac{3}{4}} \right].\)

Câu 3 (TH): Cho \(\sin \alpha  = \frac{1}{{\sqrt 3 }}\) với \(0 < \alpha  < \frac{\pi }{2}.\) Tính giá trị của \(\sin \left( {\alpha  + \frac{\pi }{3}} \right).\)

A. \(\frac{{\sqrt 3 }}{6} - \frac{{\sqrt 2 }}{2}.\)

B. \(\frac{{\sqrt 3 }}{3} - \frac{1}{2}.\)

C. \(\frac{{\sqrt 3 }}{6} + \frac{{\sqrt 2 }}{2}.\)

D. \(\sqrt 6  - \frac{1}{2}.\)

Câu 4 (TH): Tính phương sai của dãy số liệu thống kê: \(1,\,\,2,\,\,3,\,\,4,\,\,5,\,\,6,\,\,7.\)

A. \(1.\)       B. \(2.\)      C. \(3.\)      D. \(4.\)

Câu 5 (TH): Tam giác  \(ABC\)  có \(AC = 10\,cm,\,\,AB = 16\,cm{\rm{,}}\,\,\,\angle A = {60^0}.\) Độ dài cạnh \(BC\)  là

A. \(\sqrt {356 + 160\sqrt 3 } \,{\rm{cm}}{\rm{.}}\)

B. \(2\sqrt {89} \,{\rm{cm}}{\rm{.}}\)

C. \(14\,{\rm{cm}}{\rm{.}}\)

D. \(2\sqrt {129} \,{\rm{cm}}{\rm{.}}\)

Câu 6 (VD): Một cửa hàng làm kệ sách và bàn làm việc. Mỗi kệ sách cần 5 giờ chế biến gỗ và 4 giờ hoàn thiện. Mỗi bàn làm việc cần 10 giờ chế biến gỗ và 3 giờ hoàn thiện. Mỗi tháng cửa hàng có không quá 600 giờ để chế biến gỗ và không quá 24 giờ để hoàn thiện. Lợi nhuận của mỗi kệ sách là 400 nghìn đồng và mỗi bàn là 750 nghìn đồng. Hỏi mỗi tháng phải làm bao nhiêu kệ sách và bàn làm việc để cửa hàng thu được lợi nhuận tối đa?

A. 48 kệ sách và 24 bàn làm việc.

B. 60 kệ sách và 60 bàn làm việc.                                

C. 24 kệ sách và 48 bàn làm việc.

D. 0 kệ sách và 60 bàn làm việc.

Câu 7 (NB): Trong mặt phẳng với hệ tọa độ \(Oxy\), gọi \(\alpha \) là góc giữa hai đường thẳng \(x + 2y - \sqrt 2  = 0\) và\(x - y = 0\). Tính \(\cos \alpha \). 

A. \(\cos \alpha  = \frac{{\sqrt 3 }}{3}.\)

B. \(\cos \alpha  = \frac{{\sqrt {10} }}{{10}}.\)

C. \(\cos \alpha  = \frac{{\sqrt 2 }}{2}.\)

D. \(\cos \alpha  = \frac{{\sqrt 2 }}{3}.\)

Câu 8 (TH): Trong mặt phẳng với hệ tọa độ \(Oxy\), phương trình nào dưới đây là phương trình đường tròn?

A. \({x^2} + {y^2} + x + y + 4 = 0.\)

B. \({x^2} - {y^2} + 4x - 6y - 2 = 0.\)                

C. \({x^2} + 2{y^2} - 2x + 4y - 1 = 0.\)

D. \({x^2} + {y^2} - 4x - 1 = 0.\)

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1 (TH). (2,0 điểm). Giải các bất phương trình:

a) \(\frac{{{x^2} - 12x + 32}}{{5 - x}} \le 0.\)

b) \(\sqrt {{x^2} + 2x - 3}  \le 2x - 2.\)

Bài 2 (TH). (1,0 điểm). Chứng minh biểu thức

\(A = \sin 7x - 2\sin x\left( {\cos 4x + \cos 6x} \right)\)\(- \cos \left( {3x - \frac{\pi }{2}} \right) + 1\)  không phụ thuộc vào \(x.\)

Bài 3 (VD). (1,0 điểm). Cho biểu thức \(f\left( x \right) = \left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 3\left( {m - 2} \right),\) với \(m\) là tham số. Xác định \(m\) để \(f\left( x \right) \le 0\) với mọi \(x\) thuộc \(\mathbb{R}.\)

Bài 4 (VD). (3,0 điểm). Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác ABC với \(A\left( {1;2} \right),B\left( {0;1} \right),C\left( { - 2;1} \right).\)

a) Viết phương trình đường thẳng \(d\) đi qua hai điểm \(A\)  và \(B.\)

b) Tính khoảng cách từ điểm \(C\)  đến đường thẳng \(d\). Viết phương trình đường tròn tâm \(C\)  cắt đường thẳng \(d\) tại hai điểm \(E,\,\,F\)  biết \(EF = 2\sqrt 2 .\)

c) Tìm điểm \(M\) trên đường thẳng \(\Delta :x + y + 2 = 0\) sao cho \(\left| {\overrightarrow {MA}  + 2\overrightarrow {MB}  + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất.

Bài 5 (VDC). (1,0 điểm).

Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} + 2\left( {3 - m} \right)x + 1 - 4\sqrt {2{x^3} + 2x}  \ge 0\) nghiệm đúng với mọi \(x \ge 0.\)

Lời giải chi tiết

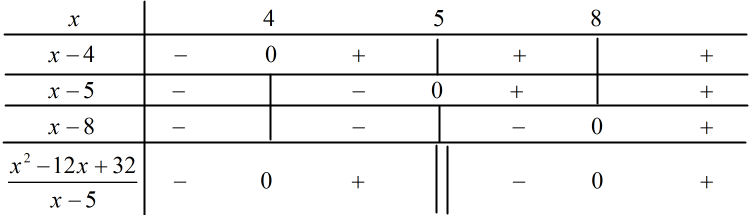
Câu 1 (TH)

Phương pháp:

Giải bất phương trình bằng phương pháp đưa về phương trình tích hoặc xét dấu của tam thức bậc hai teho quy tắc: “Trong trái ngoài cùng”.

Cách giải:

\(\begin{array}{l} - {x^2} - 4x + 5 \ge 0 \Leftrightarrow  - \left( {x - 1} \right)\left( {x + 5} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 5} \right) \le 0 \Leftrightarrow  - 5 \le x \le 1.\end{array}\)

Vậy \(S = \left[ { - 5;1} \right].\)

Chọn C.

Câu 2 (TH)

Phương pháp:

Giải hệ hai bất phương trình bậc nhất một ẩn.

Cách giải:

\(\begin{array}{l}\left\{ \begin{array}{l}2x - 1 \ge 0\\4 - 3x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x \ge 1\\3x \le 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{2}\\x \le \frac{4}{3}\end{array} \right. \Leftrightarrow \frac{1}{2} \le x \le \frac{4}{3}.\end{array}\)

Vậy \(S = \left[ {\frac{1}{2};\frac{4}{3}} \right].\)

Chọn B.

Câu 3 (TH)

Phương pháp:

Sử dụng công thức cộng: \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b.\)

Cách giải:

Ta có: \(\sin \alpha  = \frac{1}{{\sqrt 3 }}\) mà \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \Rightarrow {\cos ^2}\alpha  = \frac{2}{3}.\)

Lại có \(0 < \alpha  < \frac{\pi }{2}\) nên \(\cos \alpha  > 0 \Rightarrow \cos \alpha  = \sqrt {\frac{2}{3}} \)

\(\begin{array}{l} \Rightarrow \sin \left( {\alpha  + \frac{\pi }{3}} \right) = \sin \alpha \cos \frac{\pi }{3} + \cos \alpha \sin \frac{\pi }{3}\\\, = \frac{1}{{\sqrt 3 }}.\frac{1}{2} + \cos \alpha .\frac{{\sqrt 3 }}{2}\\ = \frac{1}{{\sqrt 3 }}.\frac{1}{2} + \sqrt {\frac{2}{3}} .\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{6} + \frac{{\sqrt 2 }}{2}.\end{array}\)

Chọn C.

Câu 4 (TH)

Phương pháp:

Sử dụng công thức tính phương sai \({s^2} = \frac{1}{n}{\sum\limits_{i = 1}^n {\left( {{x_i} - \overline x } \right)} ^2}\) với \(\overline x \) là trung bình cộng của  số liệu đã cho.

Cách giải:

Ta có: \(\overline x  = \frac{{1 + 2 + 3 + ... + 7}}{7} = 4.\)

\( \Rightarrow {s^2} = \frac{1}{n}{\sum\limits_{i = 1}^n {\left( {{x_i} - \overline x } \right)} ^2}\)\( = \frac{{{{\left( {1 - 4} \right)}^2} + {{\left( {2 - 4} \right)}^2} + ... + {{\left( {7 - 4} \right)}^2}}}{7} = 4\)

Chọn D.

Câu 5 (TH)

Phương pháp:

Sử dụng định lý hàm số cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A.\)

Cách giải:

Áp dụng định lý hàm số cos cho \(\Delta ABC\) ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2AB.AC\cos \widehat {BAC}\\\,\,\, = {10^2} + {16^2} - 2.10.16.\cos 60^\circ  = 196\\ \Rightarrow BC = 14\,{\rm{cm}}{\rm{.}}\end{array}\)

Chọn C.

Câu 6 (VD)

Phương pháp:

Giải bài toán bằng cách lập hệ bất phương trình bậc nhất hai ẩn.

Gọi số kệ sách và số bàn làm việc cửa hàng cần làm trong một tháng lần lượt là \(a,b\) với \(a,b \in \mathbb{N}.\)

Dựa vào các giả thiết của đề bài để lập hệ bất phương trình bậc nhất hai ẩn rồi giải hệ đó.

Cách giải:

Gọi số kệ sách và số bàn làm việc cửa hàng cần làm trong một tháng lần lượt là \(a,b\) với \(a,b \in \mathbb{N}.\)

Lợi nhuận cửa hàng thu được là: \(400a + 750b\) (nghìn đồng).

Để làm \(a\) kệ sách và \(b\) bàn làm việc, cần \(5a + 10b\) giờ chế biến gỗ và \(4a + 3b\) giờ hoàn thiện.

Vì mỗi tháng cửa hàng có không quá 600 giờ để chế biến gỗ và không quá 24 giờ để hoàn thiện nên ta có hệ bất phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}5a + 10b \le 600\\4a + 3b \le 240\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + 2b \le 120\\4a + 3b \le 240\end{array} \right.\\ \Rightarrow 36\left( {a + 2b} \right) + \left( {4a + 3b} \right) \le 36.120 + 240\\ \Rightarrow 40a + 75b \le 4560.\end{array}\)

Suy ra \(400a + 750b \le 45600\) nghìn đồng hay 45,6 triệu đồng.

Vậy số tiền lớn nhất có thể thu được sau 1 tháng là 45,6 triệu đồng khi:

\(\left\{ \begin{array}{l}a + 2b = 120\\4a + 3b = 240\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 24\\b = 48\end{array} \right.\) hay cửa hàng cần làm 24 kệ sách và 48 bàn làm việc.

Chọn C.

Câu 7 (TH)

Phương pháp:

Cho hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) có hai VTPT lần lượt là \(\overrightarrow {{n_1}}  = \left( {{a_1};\,\,{b_1}} \right)\) và \(\overrightarrow {{n_2}}  = \left( {{a_2};\,\,{b_2}} \right).\)

Khi đó góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) được tính bởi công thức:

\(\cos \left( {{\Delta _1};{\Delta _2}} \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}.\)

Cách giải:

Ta có: \({d_1}:\,\,x + 2y - \sqrt 2  = 0\) có VTPT là: \(\overrightarrow {{n_1}}  = \left( {1;\,\,2} \right).\)

           \({d_2}:\,\,\,x - y = 0\) có VTPT là: \(\overrightarrow {{n_2}}  = \left( {1; - 1} \right).\)

\( \Rightarrow \cos \alpha  = \frac{{\left| {\overrightarrow {{n_1}} .\,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {1.1 + 2.\left( { - 1} \right)} \right|}}{{\sqrt {{1^2} + {2^2}} .\sqrt {{1^2} + {1^2}} }} = \frac{{\sqrt {10} }}{{10}}.\)

Chọn B.

Câu 8 (NB)

Phương pháp:

Phương trình \({x^2} + {y^2} + 2ax + 2by + c = 0\) là phương trình đường tròn nếu \({a^2} + {b^2} - c > 0.\)

Cách giải:

Xét đáp án A: \({x^2} + {y^2} + x + y + 4 = 0\) có: \(a =  - \frac{1}{2};\,\,b =  - \frac{1}{2};\,\,c = 4\) \( \Rightarrow {a^2} + {b^2} - c = \frac{1}{4} + \frac{1}{4} - 4 < 0\) \( \Rightarrow \) phương trình đã cho không phải phương trình đường tròn \( \Rightarrow \) loại đáp án A.

Xét đáp án B: \({x^2} - {y^2} + 4x - 6y - 2 = 0\) không là phương trình đường tròn vì hệ số của \({x^2}\) và \({y^2}\) trái dấu nhau \( \Rightarrow \) loại đáp án B.

Xét đáp án C: \({x^2} + 2{y^2} - 2x + 4y - 1 = 0\) không là phương trình đường tròn vì hệ số của \({x^2}\) và \({y^2}\) khác nhau \( \Rightarrow \) loại đáp án C.

Xét đáp án D: \({x^2} + {y^2} - 4x - 1 = 0\) có \(a = 2;\,\,b = 0;\,\,c =  - 1\) \( \Rightarrow {a^2} + {b^2} - c = 4 + 1 = 5 > 0\) \( \Rightarrow \) phương trình đã cho là phương trình đường tròn.

Chọn D.

II. TỰ LUẬN

Bài 1 (VD)

Phương pháp:

a) Giải bất phương trình bằng quy tắc xét dấu của tam thức bậc hai và nhị thức bậc nhất.

b) Giải bất phương trình: \(\sqrt {f\left( x \right)}  \le g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) \ge 0\\f\left( x \right) \le {g^2}\left( x \right)\end{array} \right.\)

Cách giải:

a) \(\frac{{{x^2} - 12x + 32}}{{5 - x}} \le 0 \Leftrightarrow \frac{{\left( {x - 4} \right)\left( {x - 8} \right)}}{{x - 5}} \ge 0\)

Ta có bảng xét dấu:

Dựa vào bảng xét dấu ta có: \(\frac{{{x^2} - 12x + 32}}{{x - 5}} \ge 0 \Leftrightarrow \left[ \begin{array}{l}4 \le x < 5\\x \ge 8\end{array} \right..\)

Vậy tập nghiệm của bất phương trình là: \(S = \left[ {4;\,\,5} \right)\, \cup \left[ {8; + \infty } \right).\)

b)\(\sqrt {{x^2} + 2x - 3}  \le 2x - 2\)\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x - 3 \ge 0\\2x - 2 \ge 0\\{x^2} + 2x - 3 \le {\left( {2x - 2} \right)^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {x + 3} \right) \ge 0\\x - 1 \ge 0\\{x^2} + 2x - 3 \le 4{x^2} - 8x + 4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge 1\\x \le  - 3\end{array} \right.\\x \ge 1\\3{x^2} - 10x + 7 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x \ge \frac{7}{3}\\x \le 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge \frac{7}{3}\\x = 1\end{array} \right..\)

Vậy tập nghiệm của bất phương trình là: \(S = \left[ {\frac{7}{3}; + \infty } \right) \cup \left\{ 1 \right\}.\)

Bài 2 (VD)

Phương pháp:

Sử dụng công thức thức lượng giác: \(\left\{ \begin{array}{l}\cos \left( {a - b} \right) = \cos a\cos b + \sin a\sin b\\\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\\\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a - b} \right) + \sin \left( {a + b} \right)} \right]\\\sin 2x = 2\sin x\cos x\\\sin \left( { - x} \right) =  - \sin x.\end{array} \right..\)

Cách giải:

\(\begin{array}{l}A = \sin 7x - 2\sin x\left( {\cos 4x + \cos 6x} \right)\\ - \cos \left( {3x - \frac{\pi }{2}} \right) + 1\\A = \sin 7x - 2\sin x\left( {2\cos 5x.\cos x} \right)\\ - \left( {\cos 3x.\cos \frac{\pi }{2} + \sin 3x.\sin \frac{\pi }{2}} \right) + 1\\A = \sin 7x - 2.\left( {2\sin x.\cos x} \right).\cos 5x\\ - \left( {0 + \sin 3x} \right) + 1\\A = \sin 7x - 2.\sin 2x.\cos 5x - \sin 3x + 1\\A = \sin 7x - \left[ {\sin 7x + \sin \left( { - 3x} \right)} \right] - \sin 3x + 1\\A = \sin 7x - \sin 7x - \sin \left( { - 3x} \right) - \sin 3x + 1\\A = \sin 3x - \sin 3x + 1\\A = 1.\end{array}\)

Vậy giá trị của biểu thức \(A\) không phụ thuộc vào biến \(x.\)

Bài 3 (VD) 

Phương pháp:

Xét biểu thức: \(f\left( x \right) = a{x^2} + bx + c\)

+) TH1: \(a = 0,\) xét xem \(f\left( x \right) \le 0\)  với mọi \(x \in \mathbb{R}\) hay không.

+) TH2: \(a \ne 0 \Rightarrow f\left( x \right) \le 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta ' \le 0\end{array} \right..\)

Cách giải:

\(f\left( x \right) = \left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 3\left( {m - 2} \right).\)

TH1: Với \(m - 1 = 0 \Leftrightarrow m = 1\) ta có: \(f\left( x \right) =  - 4x - 3\)

\( \Rightarrow f\left( x \right) \le 0 \Leftrightarrow  - 4x - 3 \le 0 \Leftrightarrow x \ge  - \frac{3}{4}\)

\( \Rightarrow m = 1\) không thỏa mãn yêu cầu bài toán.

TH2: Với \(m - 1 \ne 0 \Leftrightarrow m \ne 1\) ta có \(f\left( x \right)\) là tam thức bậc hai.

\( \Rightarrow f\left( x \right) \le 0\,\,\forall m \Leftrightarrow \left\{ \begin{array}{l}m - 1 < 0\\\Delta ' \le 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\{\left( {m + 1} \right)^2} - 3\left( {m - 1} \right)\left( {m - 2} \right) \le 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\{m^2} + 2m + 1 - 3{m^2} + 9m - 6 \le 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\2{m^2} - 11m + 5 \ge 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\\left( {2m - 1} \right)\left( {m - 5} \right) \ge 0\end{array} \right.\)  \( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\\left[ \begin{array}{l}m \ge 5\\m \le \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow m \le \frac{1}{2}.\)

Vậy với \(m \le \frac{1}{2}\) thì \(f\left( x \right) \le 0\) với \(\forall x \in \mathbb{R}.\)

Bài 4 (VD) 

Phương pháp:

a) Phương trình đường thẳng \(\Delta \) có vecto pháp tuyến \(\overrightarrow n \left( {a;\,\,b} \right)\) và đi qua điểm \(M\left( {{x_M};\,\,{y_M}} \right)\) có dạng: \(\Delta :\,\,\,a\left( {x - {x_M}} \right) + b\left( {y - {y_M}} \right) = 0.\)

b) Cho điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) và đường thẳng \(\Delta :\,\,\,ax + by + c = 0\) ta có: \(d\left( {M;\,\,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)  

Sau đó dùng định lý Py-ta-go để tìm bán kính.

c) Gọi \(I\left( {m;\,\,n} \right)\) là điểm thỏa mãn \(\overrightarrow {IA}  + 2\overrightarrow {IB}  + \overrightarrow {IC}  = \overrightarrow 0 \), từ đó tìm tọa độ điểm \(I\) sau đó tìm tọa độ điểm \(M.\)

Cách giải:

Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác ABC với \(A\left( {1;2} \right),B\left( {0;1} \right),C\left( { - 2;1} \right).\)

a) Viết phương trình đường thẳng \(d\) đi qua hai điểm \(A\)  và \(B.\)

Ta có: \(\overrightarrow {AB} \left( { - 1; - 1} \right) \Rightarrow \overrightarrow n  = \left( {1; - 1} \right)\) là VTPT của đường thẳng \(d.\)

\( \Rightarrow d:1\left( {x - 1} \right) - 1\left( {y - 2} \right) = 0 \)\(\Leftrightarrow x - y + 1 = 0.\)    

Vậy phương trình đường thẳng \(d:\,\,x - y + 1 = 0.\)

b) Tính khoảng cách từ điểm \(C\)  đến đường thẳng \(d\). Viết phương trình đường tròn tâm \(C\)  cắt đường thẳng \(d\) tại hai điểm \(E,\,\,F\)  biết \(EF = 2\sqrt 2 .\)

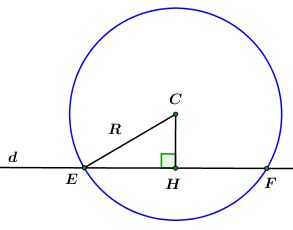
Ta có: \(d:\,\,x - y + 1 = 0.\)

Khoảng cách từ điểm C đến đường thẳng \(d\) là: \(d\left( {C,d} \right) = \frac{{\left| { - 2 - 1 + 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \sqrt 2 .\)

Gọi \(H\) là hình chiếu của \(C\) trên \(d\)

\( \Rightarrow CH = \sqrt 2 .\)

Gọi \(R\) là bán kính của đường tròn cần tìm.

Áp dụng định lý Pitago cho \(\Delta CEH\) vuông tại \(H\) ta có:

\({R^2} = C{H^2} + {\left( {\frac{{EF}}{2}} \right)^2} \)\(\Leftrightarrow {R^2} = 2 + {\left( {\frac{{2\sqrt 2 }}{2}} \right)^2} = 4 \Rightarrow R = 2.\)

Vậy đường tròn cần tìm có phương trình là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 4.\)

c) Tìm điểm \(M\) trên đường thẳng \(\Delta :x + y + 2 = 0\) sao cho \(\left| {\overrightarrow {MA}  + 2\overrightarrow {MB}  + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất.

Gọi \(M\left( {a; - a - 2} \right) \in \Delta .\)

Gọi \(G\) là trọng tâm tam giác \(ABC \Rightarrow G\left( { - \frac{1}{3};\frac{4}{3}} \right).\)

Gọi \(I\left( {m;\,\,n} \right)\) là điểm thỏa mãn \(\overrightarrow {IA}  + 2\overrightarrow {IB}  + \overrightarrow {IC}  = \overrightarrow 0 \)\( \Leftrightarrow 3\overrightarrow {IG}  + \overrightarrow {IB}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {IB}  =  - 3\overrightarrow {IG} \)

\( \Leftrightarrow \left\{ \begin{array}{l}0 - m =  - 3\left( { - \frac{1}{3} - m} \right)\\1 - n =  - 3\left( {\frac{4}{3} - n} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}m =  - \frac{1}{4}\\n = \frac{5}{4}\end{array} \right. \Rightarrow I\left( { - \frac{1}{4};\frac{5}{4}} \right).\)

Có \(\left| {\overrightarrow {MA}  + 2\overrightarrow {MB}  + \overrightarrow {MC} } \right|\)\( = \left| {4\overrightarrow {MI}  + \overrightarrow {IA}  + 2\overrightarrow {IB}  + \overrightarrow {IC} } \right| = 4MI\)

\(\begin{array}{l}\overrightarrow {MI}  = \left( { - \frac{1}{4} - a;\frac{5}{4} + a + 2} \right)\\ \Rightarrow MI = \sqrt {{{\left( { - \frac{1}{4} - a} \right)}^2} + {{\left( {a + \frac{{13}}{4}} \right)}^2}} \\ = \sqrt {2{a^2} + 7a + \frac{{85}}{8}} \\ = \sqrt {2{{\left( {a + \frac{7}{4}} \right)}^2} + \frac{9}{2}}  \ge \sqrt {\frac{9}{2}} .\end{array}\)

Vậy \(\left| {\overrightarrow {MA}  + 2\overrightarrow {MB}  + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất là \(\frac{{3\sqrt 2 }}{2}\) khi \(a =  - \frac{7}{4}\) hay \(M\left( { - \frac{7}{4}, - \frac{1}{4}} \right).\)

Bài 5 (VDC)

Cách giải:

\({x^2} + 2\left( {3 - m} \right)x + 1 - 4\sqrt {2{x^3} + 2x}  \ge 0\).

Điều kiện xác định: \(x \ge 0.\)

Bất phương trình tương đương với: \({x^2} + 6x + 1 - 4\sqrt {2{x^3} + 2x}  \ge 2mx\,\,\,\left( 1 \right).\)

Với \(x = 0,\,\,\,\left( 1 \right) \Leftrightarrow 1 \ge 0,\) luôn đúng với mọi \(m.\)

Với \(x > 0,\,\,\left( 1 \right) \Leftrightarrow x + 6 + \frac{1}{x} - 4\sqrt {2x + \frac{2}{x}}  \ge 2m.\)

Đặt \(\sqrt {2\left( {x + \frac{1}{x}} \right)}  = t,\,\,\,x > 0 \Rightarrow t \ge 2\) (theo AM-GM).

\( \Rightarrow x + 6 + \frac{1}{x} - 4\sqrt {2x + \frac{2}{x}}  = \frac{1}{2}{t^2} - 4t + 6\) \( = \frac{1}{2}\left( {{t^2} - 8t} \right) + 6 = \frac{1}{2}{\left( {t - 4} \right)^2} - 2 \ge  - 2\)

Dấu bằng xảy ra khi \(t = 4 \Leftrightarrow 2\left( {x + \frac{1}{x}} \right) = 16\)

\(\begin{array}{l} \Leftrightarrow 2x + \frac{2}{x} - 16 = 0 \Leftrightarrow 2{x^2} - 16x + 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 4 + \sqrt {15} \,\,\,\left( {tm} \right)\\x = 4 - \sqrt {15} \,\,\,\left( {tm} \right)\end{array} \right..\end{array}\)  

Vậy \(x + 6 + \frac{1}{x} - 4\sqrt {2x + \frac{2}{x}}  \ge  - 2,\forall x > 0.\)

Vậy để bất phương trình \({x^2} + 2\left( {3 - m} \right)x + 1 - 4\sqrt {2{x^3} + 2x}  \ge 0\) đúng với mọi \(x \ge 0\) thì \(2m \le  - 2 \Leftrightarrow m \le  - 1.\)

Nguồn: Sưu tầm

HocTot.Nam.Name.Vn