Đề số 2 – Đề kiểm tra học kì 2 – Toán 8

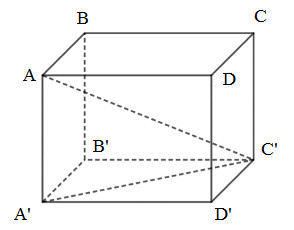
Đề bài

Câu 1 (VD) (3,5 điểm). Giải các phương trình và bất phương trình sau:

a) \(3x - 11 = x + 7\)

b) \(2x\left( {x - 3} \right) = x - 3\)

c) \(\dfrac{{x + 2}}{{x - 2}} - \dfrac{5}{x} = \dfrac{8}{{{x^2} - 2x}}\)

d) \(\dfrac{{2x + 1}}{4} - \dfrac{{x - 5}}{3} \le \dfrac{{4x - 1}}{{12}} + 2\)

Câu 2 (VD) (2,0 điểm). Giải bài toán bằng cách lập phương trình

Một xe máy khởi hành từ A để đi đến B với vận tốc 30 km/h. Sau khi xe máy đi được 20 phút, trên cùng tuyến đường đó, một ô tô khởi hành từ B để đi đến A với vận tốc 45 km/h, biết quãng đường AB dài 90 km. Hỏi sau bao lâu kể từ lúc ô tô khởi hành thì hai xe gặp nhau?

Câu 3 (VD) (1,0 điểm).

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có \(AB = 10cm,BC = 20cm,AA' = 15cm\).

a) Tính diện tích toàn phần của hình hộp chữ nhật

b) Tính độ dài đường chéo AC’ của hình hộp chữ nhật (làm tròn đến chữ số thập phân thứ nhất)

Câu 4 (VD) (3,0 điểm). Cho tam giác ABC vuông tại A, đường cao AH.

a) Chứng minh \(\Delta ABH\) đồng dạng với \(\Delta CBA\).

b) Cho \(BH = 4cm,BC = 13cm\). Tính độ dài đoạn AB.

c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. Chứng minh \(AE.CH = AH.FC\)

d) Tìm vị trí của điểm E trên cạnh AB để tam giác EHF có diện tích nhỏ nhất.

Câu 5 (VDC) (0,5 điểm). Chứng minh rằng nếu a, b, c là các số dương và  \(a + b + c = 1\) thì:

\({\left( {a + \dfrac{1}{a}} \right)^2} + {\left( {b + \dfrac{1}{b}} \right)^2} + {\left( {c + \dfrac{1}{c}} \right)^2} > 33\)

LG câu 1

Phương pháp giải:

a) Chuyển vế đổi dấu

b) Biến đổi phương trình thành phương trình tích để giải

c) Quy đồng khử mẫu, rút gọn

d) Quy đồng khử mẫu, nhân phá ngoặc, rút gọn BPT

Lời giải chi tiết:

\(\begin{array}{l}a)\,\,\,3x - 11 = x + 7\\ \Leftrightarrow 2x = 18 \Leftrightarrow x = 9\end{array}\)

Vậy nghiệm của phương trình là \(x = 9.\)                                                     

\(\begin{array}{l}b)\,\,\,2x\left( {x - 3} \right) = x - 3\\ \Leftrightarrow 2x\left( {x - 3} \right) - \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {2x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\2x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\2x = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{1}{2}\end{array} \right.\end{array}\)

Vậy nghiệm của phương trình là \(x \in \left\{ {3;\dfrac{1}{2}} \right\}.\)

\(c)\,\,\,\dfrac{{x + 2}}{{x - 2}} - \dfrac{5}{x} = \dfrac{8}{{{x^2} - 2x}}\)             

ĐKXĐ: \(\left\{ \begin{array}{l}x - 2 \ne 0\\x \ne 0\\{x^2} - 2x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne 0\\x\left( {x - 2} \right) \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne 0\end{array} \right.\)

\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{x + 2}}{{x - 2}} - \dfrac{5}{x} = \dfrac{8}{{{x^2} - 2x}}\\ \Leftrightarrow \dfrac{{x + 2}}{{x - 2}} - \dfrac{5}{x} - \dfrac{8}{{x\left( {x - 2} \right)}} = 0\\ \Leftrightarrow \dfrac{{x\left( {x + 2} \right)}}{{x\left( {x - 2} \right)}} - \dfrac{{5\left( {x - 2} \right)}}{{x\left( {x - 2} \right)}} - \dfrac{8}{{x\left( {x - 2} \right)}} = 0\\ \Leftrightarrow \dfrac{{{x^2} + 2x - 5x + 10 - 8}}{{x\left( {x - 2} \right)}} = 0\\ \Leftrightarrow \dfrac{{{x^2} - 3x + 2}}{{x\left( {x - 2} \right)}} = 0\\ \Leftrightarrow \dfrac{{\left( {x - 1} \right)\left( {x - 2} \right)}}{{x\left( {x - 2} \right)}} = 0\\ \Leftrightarrow \dfrac{{x - 1}}{x} = 0 \Leftrightarrow x - 1 = 0\\ \Leftrightarrow x = 1\,\,\,\left( {tm} \right)\end{array}\)                              

Vậy nghiệm của phương trình là \(x = 1.\) 

\(\begin{array}{l}d)\,\,\,\dfrac{{2x + 1}}{4} - \dfrac{{x - 5}}{3} \le \dfrac{{4x - 1}}{{12}} + 2\\ \Leftrightarrow \dfrac{{3\left( {2x + 1} \right)}}{{12}} - \dfrac{{4\left( {x - 5} \right)}}{{12}} \le \dfrac{{4x - 1}}{{12}} + \dfrac{{24}}{{12}}\\ \Leftrightarrow 6x + 3 - 4x + 20 \le 4x - 1 + 24\\ \Leftrightarrow 2x \ge 0 \Leftrightarrow x \ge 0\end{array}\)

Vậy BPT có tập nghiệm \(S = \left\{ {x|x \ge 0} \right\}.\)

LG câu 2

Phương pháp giải:

Gọi thời gian để 2 xe gặp nhau kể từ lúc ô tô khởi hành là x (giờ).

Biết vận tốc của từng xe trên từng quãng đường 

\( \Rightarrow \) lập phương trình theo tổng quãng đường để tìm x.

Lời giải chi tiết:

Gọi thời gian để 2 xe gặp nhau kể từ lúc ô tô khởi hành là x (giờ) \(\left( {x > 0} \right).\)

Đổi 20 phút = \(\dfrac{1}{3}\) giờ

Quãng đường xe máy đi được trong 20 phút đầu là \(30.\dfrac{1}{3} = 10\,\,\left( {km} \right).\)

Quãng đường xe máy đi từ khi ô tô khởi hành đến khi 2 xe gặp nhau là \(30x\,\,\,\left( {km} \right).\)

Quãng đường ô tô đi đến chỗ gặp nhau với xe máy là \(45x\,\,\,\left( {km} \right).\)

Vì quãng đường AB dài 90 km nên ta có phương trình: 

\(10 + 30x + 45x = 90 \Leftrightarrow 75x = 80 \Leftrightarrow x = \dfrac{{16}}{{15}}\)  (giờ)

Vậy sau \(\dfrac{{16}}{{15}}\) giờ = 1 giờ 4 phút kể từ lúc ô tô khởi hành thì hai xe gặp nhau.

LG câu 3

Phương pháp giải:

a) Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích tất cả các mặt của hình hộp chữ nhật đó.

b) Áp dụng định lý Py-ta-go để tính A’C’ từ đó tính AC’.

Lời giải chi tiết:

a) Tính diện tích toàn phần của hình hộp chữ nhật

\(\begin{array}{l}{S_{tp}} = 2AB.AD + 2AA'\left( {AB + AD} \right)\\ = 2.10.20 + 2.15.\left( {10 + 20} \right)\\ = 400 + 900 = 1300\,\,c{m^2}.\end{array}\)  

b) Tính độ dài đường chéo AC’ của hình hộp chữ nhật (làm tròn đến chữ số thập phân thứ nhất)

Áp dụng định lý Py-ta-go cho \(\Delta A'B'C'\) vuông tại B’  ta có:

\(A'C{'^2} = A'B{'^2} + B'C{'^2}\) \( = A{B^2} + B{C^2} = {20^2} + {10^2} = 500\)

Áp dụng định lý Py-ta-go cho \(\Delta AA'C'\) vuông tại A’ ta có:

\(AC{'^2} = AA{'^2} + A'C{'^2}\)\( = {15^2} + 500 = 725\) \( \Rightarrow AC' = \sqrt {725}  \approx 26,9\,\,cm.\)

LG câu 4

Phương pháp giải:

a) Chứng minh \(\Delta ABH \backsim \Delta CBA\,\,\left( {g - g} \right)\)

b) Từ a) suy ra công thức để tính AB theo BC và BH

c) Chứng minh \(\Delta EHA \backsim \Delta FHC\,\,\left( {g - g} \right)\)  từ đó suy ra tỉ lệ các cạnh suy ra đpcm

d) Chứng minh \(\Delta EHF \backsim \Delta BAC\,\,\left( {c - g - c} \right)\)  với tỉ số đồng dạng \(k = \dfrac{{HE}}{{AB}}\).

Từ đó tính \({S_{EHF}}\) theo các đại lượng không đổi \({S_{ABC}}\); AB và đại lượng thay đổi HE \( \Rightarrow \) vị trí điểm E thỏa mãn yêu cầu đề bài.

Lời giải chi tiết:

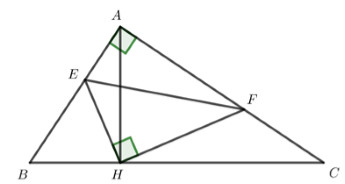
a) Chứng minh \(\Delta ABH\) đồng dạng với \(\Delta CBA\).

Ta có tam giác ABC vuông tại A \( \Rightarrow \angle BAC = {90^o}\)

Mặt khác do tam giác ABC có đường cao AH

\( \Rightarrow \angle BHA = {90^o} \Rightarrow \angle BAC = \angle BHA = {90^o}\)

Xét \(\Delta ABH\) và \(\Delta CBA\) có:

\(\begin{array}{l}\angle B\,\,\,chung\\\angle BHA = \angle BAC = {90^o}\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ABH \backsim \Delta CBA\,\,\,\left( {g - g} \right)\end{array}\)

b) Cho \(BH = 4cm,BC = 13cm\). Tính độ dài đoạn AB.

Ta có \(\Delta ABH \backsim \Delta CBA\,\,\left( {cmt} \right)\) \( \Rightarrow \dfrac{{AB}}{{BC}} = \dfrac{{BH}}{{AB}}\)  (các cặp cạnh tương ứng tỉ lệ)

\( \Rightarrow A{B^2} = BC.BH\) \( = 13.4 = 52\)

\( \Rightarrow AB = \sqrt {52} \,\,cm\) 

c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. Chứng minh \(AE.CH = AH.FC\)

Ta có \(HE \bot HF\,\,\,\left( {gt} \right) \Rightarrow \angle EHF = {90^o}.\)

\( \Rightarrow \angle EHA + \angle AHF = {90^o}\)  (1)

Mặt khác do tam giác ABC có đường cao AH

\( \Rightarrow \angle AHC = {90^o}\) (tc) \( \Rightarrow \angle FHC + \angle AHF = {90^o}\)  (2)

Từ (1) và (2) \( \Rightarrow \angle EHA = \angle FHC\) (cùng phụ với \(\angle AHF\))

Xét \(\Delta EHA\) và \(\Delta FHC\) có:

\(\begin{array}{l}\angle EHA = \angle FHC\,\,\,\,\left( {cmt} \right)\\\angle EAH = \angle FCH\,\,\,\left( {\Delta ABH \backsim \Delta CBA} \right)\\ \Rightarrow \Delta EHA \backsim \Delta FHC\,\,\,\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{AE}}{{FC}} = \dfrac{{AH}}{{CH}}\) (các cặp cạnh tương ứng tỉ lệ)

\( \Rightarrow AE.CH = AH.FC\,\,\,\left( {dpcm} \right).\) 

d) Tìm vị trí của điểm E trên cạnh AB để tam giác EHF có diện tích nhỏ nhất.

Ta có tam giác ABC vuông tại A \( \Rightarrow \angle ACH + \angle ABH = {90^o}\)

Lại có tam giác ABH vuông tại H \( \Rightarrow \angle BAH + \angle ABH = {90^o}\)

\( \Rightarrow \angle ACH = \angle BAH\)  (cùng phụ với \(\angle ABH\))

Xét \(\Delta CAH\) và \(\Delta ABH\) có:

\(\angle ACH = \angle BAH\,\,\,\left( {cmt} \right)\)

\(\angle AHC = \angle BHA = {90^o}\) (AH là đường cao của tam giác ABC)

\( \Rightarrow \Delta CAH \backsim \Delta ABH\,\,\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{AC}}{{AB}} = \dfrac{{CH}}{{AH}}\) (cặp cạnh tương ứng tỉ lệ)

Mà   \(\dfrac{{HF}}{{HE}} = \dfrac{{CH}}{{AH}}\,\)\(\,\left( {do\,\,\Delta EHA \backsim \Delta FHC} \right)\) \( \Rightarrow \dfrac{{HF}}{{HE}} = \dfrac{{AC}}{{AB}}\)

Xét \(\Delta EHF\) và \(\Delta BAC\) có:

\(\begin{array}{l}\angle EHF = \angle BAC = {90^o}\\\dfrac{{HF}}{{HE}} = \dfrac{{AC}}{{AB}}\,\,\,\left( {cmt} \right)\end{array}\)  

\( \Rightarrow \Delta EHF \backsim \Delta BAC\,\,\,\left( {c - g - c} \right)\)  với tỉ số đồng dạng \(k = \dfrac{{HE}}{{AB}}\)

\( \Rightarrow \dfrac{{{S_{EHF}}}}{{{S_{ABC}}}} = {\left( {\dfrac{{HE}}{{AB}}} \right)^2}\) \( \Rightarrow {S_{EHF}} = {S_{ABC}}.{\left( {\dfrac{{HE}}{{AB}}} \right)^2}\)

Mà \({S_{ABC}}\) và AB không đổi nên để \({S_{EHF}}\) nhỏ nhất \( \Leftrightarrow HE\) nhỏ nhất \( \Leftrightarrow HE \bot AB\)

Vậy với E là chân đường vuông góc kẻ từ H xuống AB thỏa mãn yêu cầu đề bài.

LG câu 5

Phương pháp giải:

Chứng minh với 3 số \(A,B,C > 0\) ta có \({A^2} + {B^2} + {C^2} \ge \dfrac{{{{\left( {A + B + C} \right)}^2}}}{3}\)

Đặt \(A = a + \dfrac{1}{a}\,\,;\,\,B = b + \dfrac{1}{b}\,\,;\,\,\)\(C = c + \dfrac{1}{c}\). Áp dụng chứng minh trên và giả thiết đề bài để suy ra đpcm.

Lời giải chi tiết:

Với 3 số \(A,B,C > 0\), áp dụng BĐT Cô-si ta có: \(\left\{ \begin{array}{l}{A^2} + {B^2} \ge 2AB\,\,\\{B^2} + {C^2} \ge 2BC\,\,\\{C^2} + {A^2} \ge 2AC\end{array} \right.\) \( \Rightarrow 2\left( {{A^2} + {B^2} + {C^2}} \right) \ge 2\left( {AB + BC + CA} \right).\)

Cộng từng vế của BĐT trên với \({A^2} + {B^2} + {C^2}\)

\( \Rightarrow 3\left( {{A^2} + {B^2} + {C^2}} \right) \ge {\left( {A + B + C} \right)^2}\) \( \Leftrightarrow {A^2} + {B^2} + {C^2} \ge \dfrac{{{{\left( {A + B + C} \right)}^2}}}{3}\)

Đặt \(A = a + \dfrac{1}{a}\,\,;\,\,B = b + \dfrac{1}{b}\,\,;\,\,C = c + \dfrac{1}{c}\) ta có:

\(P = {\left( {a + \dfrac{1}{a}} \right)^2} + {\left( {b + \dfrac{1}{b}} \right)^2} + {\left( {c + \dfrac{1}{c}} \right)^2}\)\( \ge \dfrac{1}{3}{\left( {a + \dfrac{1}{a} + b + \dfrac{1}{b} + c + \dfrac{1}{c}} \right)^2}\)

\(\begin{array}{l} \Leftrightarrow P \ge \dfrac{1}{3}{\left( {a + b + c + \dfrac{{a + b + c}}{a} + \dfrac{{a + b + c}}{b} + \dfrac{{a + b + c}}{c}} \right)^2}\\ \Leftrightarrow P \ge \dfrac{1}{3}{\left( {1 + 1 + \dfrac{b}{a} + \dfrac{c}{a} + 1 + \dfrac{a}{b} + \dfrac{c}{b} + 1 + \dfrac{a}{c} + \dfrac{b}{c}} \right)^2}\\ \Leftrightarrow P \ge \dfrac{1}{3}{\left( {4 + \dfrac{a}{b} + \dfrac{b}{a} + \dfrac{a}{c} + \dfrac{c}{a} + \dfrac{b}{c} + \dfrac{c}{b}} \right)^2}\end{array}\)

Áp dụng bất đẳng thức Cô-si cho hai số dương ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{a}{b} + \dfrac{b}{a} \ge 2\sqrt {\dfrac{a}{b}.\dfrac{b}{a}} \\\dfrac{b}{c} + \dfrac{c}{b} \ge 2\sqrt {\dfrac{b}{c}.\dfrac{c}{b}} \\\dfrac{c}{a} + \dfrac{a}{c} \ge 2\sqrt {\dfrac{c}{a}.\dfrac{a}{c}} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{a}{b} + \dfrac{b}{a} \ge 2\\\dfrac{b}{c} + \dfrac{c}{b} \ge 2\\\dfrac{c}{a} + \dfrac{a}{c} \ge 2\end{array} \right.\\ \Rightarrow P \ge \dfrac{1}{3}{\left( {4 + 2 + 2 + 2} \right)^2}\end{array}\)

\( \Leftrightarrow P \ge \dfrac{1}{3}{.10^2} = \dfrac{{100}}{3} > 33\,\,\)

Vậy \(P > 33\) (đpcm)

Nguồn sưu tầm

HocTot.Nam.Name.Vn