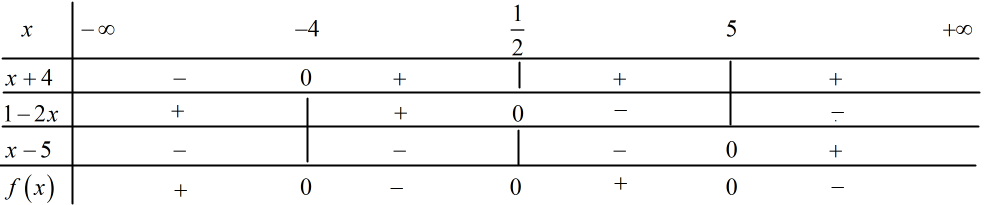Đề số 1 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10

Đề bài

Bài 1. (3 điểm)

1. Giải các bất phương trình sau :

a) \(\left( {1 - 2x} \right)\left( {{x^2} - x - 20} \right) > 0\)

b) \(\sqrt {{x^2} - x - 2}  < x - 1.\)

2. Tìm tất cả các giá trị của tham số \(m\) để biểu thức \(f\left( x \right) = {x^2} - 2\left( {m - 1} \right)x - {m^2} + m + 6\) luôn dương với mọi \(x.\)

Bài 2. (2,5 điểm)

1. Cho \(\sin \alpha  = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha  < \pi .\) Tính giá trị biểu thức \(A = 3\cos \alpha  + 2\sin \alpha .\)
2. Chứng minh rằng \(\sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} }  = \cos \frac{x}{4}\) (với \(0 < x < \frac{\pi }{2}\)).

Bài 3. (4 điểm)

1. Cho tam giác \(ABC\) có \(AB = 6,AC = 8\) và \(\angle BAC = 60^\circ .\) Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\).
2. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {1; - 3} \right)\), đường thẳng \(\left( \Delta  \right):2x - y + 3 = 0\) và đường tròn \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 25.\)

a) Tìm tọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right).\) Chứng tỏ điểm \(A\) nằm ngoài đường tròn \(\left( C \right)\).

b) Viết phương trình đường thẳng \(\left( d \right)\) đi qua điểm \(A\) và song song với đường thẳng \(\left( \Delta  \right)\).

c) Tìm tọa độ điểm \(M\) thuộc đường thẳng \(\left( \Delta  \right)\) sao cho \(IM = 2R,\) (trong đó \(I,R\) lần lượt là tâm và bán kính của đường tròn \(\left( C \right)\)).

Bài 4. (0,5 điểm)

Giải bất phương trình sau: \(\sqrt {{x^2} + 4x}  + 2\sqrt {x - 2}  \ge \sqrt {2{x^2} + 12x - 8} .\)

Lời giải chi tiết

Bài 1 (VD)

Phương pháp:

1a: Đưa về bất phương trình tích rồi lập bảng xét dấu để tìm nghiệm của bất phương trình.

1b: \(\sqrt A  < B \Leftrightarrow \left\{ \begin{array}{l}A \ge 0\\B > 0\\A < {B^2}\end{array} \right..\)

2: Xét dấu của tam thức bậc hai: \(a{x^2} + bx + c > 0\left( {a \ne 0} \right) \forall x \\ \Leftrightarrow \left\{ \begin{array}{l}\Delta  < 0\\a > 0\end{array} \right..\)

Cách giải:

1. Giải các bất phương trình sau:

a) \(\left( {1 - 2x} \right)\left( {{x^2} - x - 20} \right) > 0\)\( \Leftrightarrow \left( {1 - 2x} \right)\left( {x + 4} \right)\left( {x - 5} \right) > 0\)

Xét \(f\left( x \right) = \left( {1 - 2x} \right)\left( {x + 4} \right)\left( {x - 5} \right) = 0 \)

\(\Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{2}\\x =  - 4\\x = 5\end{array} \right.\)

Ta có bảng xét dấu :

Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ; - 4} \right) \cup \left( {\frac{1}{2};5} \right)\).

b) \(\sqrt {{x^2} - x - 2}  < x - 1 \)

\(\Leftrightarrow \left\{ \begin{array}{l}{x^2} - x - 2 \ge 0\\x - 1 > 0\\{x^2} - x - 2 < {x^2} - 2x + 1\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right)\left( {x + 1} \right) \ge 0\\x > 1\\x < 3\end{array} \right.\)

\(\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge 2\\x \le  - 1\end{array} \right.\\x > 1\\x < 3\end{array} \right. \Leftrightarrow 2 \le x < 3.\)

2. Tìm tất cả các giá trị của tham số \(m\) để biểu thức \(f\left( x \right) = {x^2} - 2\left( {m - 1} \right)x\)\( - {m^2} + m + 6\) luôn dương với mọi \(x.\)

\(\begin{array}{l}f\left( x \right) = {x^2} - 2\left( {m - 1} \right)x - {m^2} + m \\+ 6 > 0,\,\forall x\\ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {\left( {m - 1} \right)^2} \\- 1\left( { - {m^2} + m + 6} \right) < 0\\1 > 0\end{array} \right.\\ \Leftrightarrow 2{m^2} - 3m - 5 < 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {2m - 5} \right) < 0\\ \Leftrightarrow  - 1 < m < \frac{5}{2}.\end{array}\)

Vậy \( - 1 < m < \frac{5}{2}\).

Bài 2 (VD)

Phương pháp:

1. Với \(\frac{\pi }{2} < \alpha  < \pi \) ta có: \(\sin \alpha  > 0,\,\,\,\cos \alpha  < 0.\)

2. Sử dụng công thức \(\cos 2a = 2{\cos ^2}a - 1.\)

Cách giải:

1. Cho \(\sin \alpha  = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha  < \pi .\) Tính giá trị biểu thức \(A = 3\cos \alpha  + 2\sin \alpha .\)

Với \(\frac{\pi }{2} < \alpha  < \pi \) thì \(\cos \alpha  < 0.\)

Ta có: \(\left| {\cos \alpha } \right| = \sqrt {1 - {{\sin }^2}\alpha }  = \sqrt {1 - {{\left( {\frac{5}{{13}}} \right)}^2}}\)\(  = \frac{{12}}{{13}},\) mà \(\cos \alpha  < 0\) nên \(\cos \alpha =  - \frac{{12}}{{13}}.\)

\( \Rightarrow A = 3\cos \alpha  + 2\sin \alpha \\ = 3.\left( { - \frac{{12}}{{13}}} \right) + 2.\frac{5}{{13}} =  - 2.\)

2. Chứng minh rằng \(\sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} }  = \cos \frac{x}{4}\) (với \(0 < x < \frac{\pi }{2}\)).

Với \(0 < x < \frac{\pi }{2}\) thì \(\cos \frac{x}{2} > 0,\,\,\,\cos \frac{x}{4} > 0.\)

\(VT = \sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} }  \\= \sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{{\cos x + 1}}{2}} } \)\( = \sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{{\left( {2{{\cos }^2}\frac{x}{2} - 1} \right) + 1}}{2}} } \\ = \sqrt {\frac{1}{2} + \frac{1}{2}\cos \frac{x}{2}} \)

\( = \sqrt {\frac{{\cos \frac{x}{2} + 1}}{2}}  = \sqrt {\frac{{\left( {2{{\cos }^2}\frac{x}{4} - 1} \right) + 1}}{2}}\\  = \cos \frac{x}{4}.\)

Vậy  \(\sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} }  = \cos \frac{x}{4}\) với \(0 < x < \frac{\pi }{2}.\)

Bài 3 (VD)

Phương pháp:

1. Áp dụng định lý hàm số sin và định lý hàm số cos trong tam giác.

2. a) Đường tròn tâm \(I\left( {a;b} \right)\) bán kính \(R\) có phương trình: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\)

Nếu \(IA > R\) thì điểm \(A\) nằm ngoài đường tròn \(\left( C \right).\)

b) Hai đường thẳng song song với nhau thì có cùng véc-tơ pháp tuyến.

Phương trình đường thẳng \(d\) đi qua \(M\left( {{x_0};\,\,{y_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {A;\,\,B} \right)\) có dạng: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) = 0.\)

c) Lập phương trình \(IM = 2R\) theo tọa độ của \(M\) và giải phương trình.

Cách giải:

1. Cho tam giác \(ABC\) có \(AB = 6,AC = 8\) và \(\angle BAC = 60^\circ .\) Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\).

Áp dụng định lý cos trong tam giác \(ABC\) ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} \\- 2AB.AC\cos \angle BAC\\B{C^2} = {6^2} + {8^2} - 2.6.8.\cos {60^0}\\BC = 2\sqrt {13} .\end{array}\)

Áp dụng định lý hàm số sin trong tam giác \(ABC\) ta có:

\(\frac{{BC}}{{\sin \angle BAC}} = 2R\) (trong đó \(R\) là bán kính đường tròn ngoại tiếp tam giác \(BAC\)).

\( \Rightarrow \frac{{2\sqrt {13} }}{{\sin {{60}^0}}} = 2R \Rightarrow R = \frac{{2\sqrt {39} }}{3}.\)

2. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {1; - 3} \right)\), đường thẳng \(\left( \Delta  \right):2x - y + 3 = 0\) và đường tròn \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 25.\)

a) Tìm tọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right).\) Chứng tỏ điểm \(A\) nằm ngoài đường tròn \(\left( C \right)\).

\(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 25\) có tâm \(I\left( {2;\,\,3} \right)\) và bán kính \(R = 5.\)

Có \(AI = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {3 + 3} \right)}^2}}  = \sqrt {37}  > R\) nên \(A\) nằm ngoài đường tròn \(\left( C \right).\)

b) Viết phương trình đường thẳng \(\left( d \right)\) đi qua điểm \(A\) và song song với đường thẳng \(\left( \Delta  \right)\).

Đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( \Delta  \right):2x - y + 3 = 0\) nên \(\left( d \right)\) có VTPT là \(\overrightarrow n \left( {2; - 1} \right).\)

Đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1; - 3} \right)\) và có VTPT là \(\overrightarrow n \left( {2; - 1} \right)\) nên \(\left( d \right)\) có phương trình là: \(2\left( {x - 1} \right) - \left( {y + 3} \right) = 0 \)\(\Leftrightarrow 2x - y - 5 = 0.\)

Vậy \(\left( d \right):2x - y - 5 = 0.\)

c) Tìm tọa độ điểm \(M\) thuộc đường thẳng \(\left( \Delta  \right)\) sao cho \(IM = 2R,\) (trong đó \(I,R\) lần lượt là tâm và bán kính của đường tròn \(\left( C \right)\)).

Vì \(M\) thuộc đường thẳng \(\left( \Delta  \right)\) nên gọi \(M\left( {a;\,\,2a + 3} \right).\)

\(\begin{array}{l} \Rightarrow IM = 2R\\ \Leftrightarrow \sqrt {{{\left( {a - 2} \right)}^2} + {{\left( {2a + 3 - 3} \right)}^2}}  = 10\\ \Leftrightarrow \sqrt {{a^2} - 4a + 4 + 4{a^2}}  = 10\\ \Leftrightarrow 5{a^2} - 4a + 4 = 100\\ \Leftrightarrow \left[ \begin{array}{l}a = \frac{{24}}{5} \Rightarrow M\left( {\frac{{24}}{5};\frac{{63}}{5}} \right)\\a =  - 4 \Rightarrow M\left( { - 4; - 5} \right)\end{array} \right..\end{array}\)

Vậy \(M\left( {\frac{{24}}{5};\frac{{63}}{5}} \right)\) hoặc \(M\left( { - 4; - 5} \right)\) thỏa mãn yêu cầu.

Bài 4 (VDC)

Phương pháp:

Giải bất phương trình bằng phương pháp đặt ẩn phụ.

Cách giải:

\(\sqrt {{x^2} + 4x}  + 2\sqrt {x - 2} \\ \ge \sqrt {2{x^2} + 12x - 8} \,\,\left( * \right)\)  

Điều kiện: \(x \ge 2.\)

Đặt \(\left\{ \begin{array}{l}\sqrt {{x^2} + 4x}  = a\\2\sqrt {x - 2}  = b\,\,\end{array} \right..\)

Với \(x \ge 2\) thì \(a > 0,\,\,b \ge 0.\)

Ta có: \(2{x^2} + 12x - 8 = 2\left( {{x^2} + 4x} \right) \)\(+ 4\left( {x - 2} \right) = 2{a^2} + {b^2}.\)

\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow a + b \ge \sqrt {2{a^2} + {b^2}} \\ \Leftrightarrow {a^2} + 2ab + {b^2} \ge 2{a^2} + {b^2}\\ \Leftrightarrow 2ab \ge {a^2}\\ \Leftrightarrow 2b \ge a\,\,\,\,\,\left( {do\,\,\,a > 0} \right)\\ \Leftrightarrow 4\sqrt {x - 2}  \ge \sqrt {{x^2} + 4x} \\ \Leftrightarrow 16\left( {x - 2} \right) \ge {x^2} + 4x\\ \Leftrightarrow {x^2} - 12x + 32 \le 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 4 \le x \le 8.\end{array}\)

Kết hợp với điều kiện ta có \(4 \le x \le 8\) là tập nghiệm của bất phương trình.

Nguồn: Sưu tầm

HocTot.Nam.Name.Vn