Đề số 1 - Đề kiểm tra học kì 1 - Toán 9Tải vềĐáp án và lời giải chi tiết Đề số 1 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
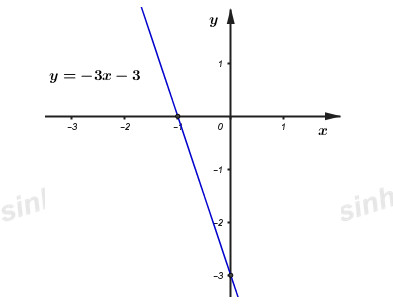
Đề bài Bài 1: (2 điểm) 1) Thực hiện phép tính: a) \(\sqrt 8 - 2\sqrt {18} + 5\sqrt {32} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \) b) \(\dfrac{{5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{7 - \sqrt 7 }}{{\sqrt 7 - 1}} - \left( {\sqrt 5 + \sqrt 7 } \right)\) 2) Giải phương trình: \(x - \sqrt {x - 15} = 17\). Bài 2: (2,5 điểm) Cho biểu thức \(P = \dfrac{{3x + \sqrt {9x} - 3}}{{x + \sqrt x - 2}} - \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}} + \dfrac{{\sqrt x - 2}}{{1 - \sqrt x }}\) với \(x \ge 0,x \ne 1\) a) Rút gọn biểu thức \(P\). b) So sánh \(P\) với \(\sqrt P \) với điều kiện \(\sqrt P \)có nghĩa c) Tìm \(x\) để \(\dfrac{1}{P}\) nguyên. Câu 3: (2 điểm) Cho đường thẳng \(\left( {{d_1}} \right) :y = \left( {m - 1} \right)x + 2m + 1\). Tìm \(m\) để đường thẳng \({d_1}\) cắt trục tung tại điểm có tung độ là \( - 3\). Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng \(\left( d \right):y = x + 1\) nằm trên trục hoành. Bài 4: (3 điểm) Cho điểm M bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của \(\left( O \right)\) cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N. a) Chứng minh \(DC = DN\). b) Chứng minh AC là tiếp tuyến của đường tròn tâm O. c) Gọi H là chân đường vuông góc kẻ từ M xuống AB, I là trung điểm MH. Chứng minh B, C, I thẳng hàng. d) Qua O kẻ đường vuông góc với AB, cắt \(\left( O \right)\) tại K (K và M nằm khác phía với đường thẳng AB ). Tìm vị trí của M để diện tích tam giác MHK lớn nhất. Bài 5: (0,5 điểm) Cho các số thực dương \(x,y,z\) thỏa mãn \(x + 2y + 3z \ge 20\). Tìm giá trị nhỏ nhất của biểu thức : \(A = x + y + z + \dfrac{3}{x} + \dfrac{9}{{2y}} + \dfrac{4}{z}\). LG bài 1 Lời giải chi tiết: Bài 1: 1) Thực hiện phép tính: \(\begin{array}{l}a)\;\;\sqrt 8 - 2\sqrt {18} + 5\sqrt {32} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \\ = \sqrt {{2^2}.2} - 2\sqrt {{3^2}.2} + 5\sqrt {{4^2}.2} - \left| {\sqrt 2 - 1} \right|\\ = 2\sqrt 2 - 2.3\sqrt 2 + 5.4\sqrt 2 - \left( {\sqrt 2 - 1} \right)\\ = 2\sqrt 2 - 6\sqrt 2 + 20\sqrt 2 - \sqrt 2 + 1\\ = 15\sqrt 2 + 1.\end{array}\) Vậy \(\sqrt 8 - 2\sqrt {18} + 5\sqrt {32} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} = 15\sqrt 2 + 1\) \(\begin{array}{l}b)\;\;\dfrac{{5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{7 - \sqrt 7 }}{{\sqrt 7 - 1}} - \left( {\sqrt 5 + \sqrt 7 } \right)\\ = \dfrac{{\sqrt 5 .\sqrt 5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{\sqrt 7 .\sqrt 7 - \sqrt 7 }}{{\sqrt 7 - 1}} - \left( {\sqrt 5 + \sqrt 7 } \right)\\ = \dfrac{{\sqrt 5 \left( {6 + \sqrt 5 } \right)}}{{\sqrt 5 }} + \dfrac{{\sqrt 7 .\left( {\sqrt 7 - 1} \right)}}{{\sqrt 7 - 1}} - \sqrt 5 - \sqrt 7 \\ = 6 + \sqrt 5 + \sqrt 7 - \sqrt 5 - \sqrt 7 = 6.\end{array}\) Vậy \(\dfrac{{5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{7 - \sqrt 7 }}{{\sqrt 7 - 1}} - \left( {\sqrt 5 + \sqrt 7 } \right) = 6\) 2) Giải phương trình: \(x - \sqrt {x - 15} = 17\). ĐKXĐ: \(x \ge 15\) \(\begin{array}{l}\;\;\;\;\;x - \sqrt {x - 15} = 17\\ \Leftrightarrow x - 17 = \sqrt {x - 15} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 17 \ge 0\\{\left( {x - 17} \right)^2} = {\left( {\sqrt {x - 15} } \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 17\\{x^2} - 34x + 289 = x - 15\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 17\\{x^2} - 35x + 304 = 0\end{array} \right.\end{array}\) Xét phương trình \({x^2} - 35x + 304 = 0\), ta có: \({x^2} - 35x + 304 = 0\\{x^2} - 16 x - 19x + 304 = 0 \\ x(x - 16) - 19(x - 16) = 0 \\ (x-19)(x-16)=0\\\Leftrightarrow \left[ \begin{array}{l}x=19 (TM)\\x=16 (L)\end{array} \right.\) Vậy phương trình đã cho có nghiệm duy nhất là \(x = 19\). LG bài 2 Lời giải chi tiết: Cho biểu thức \(P = \dfrac{{3x + \sqrt {9x} - 3}}{{x + \sqrt x - 2}} - \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}} + \dfrac{{\sqrt x - 2}}{{1 - \sqrt x }}\) với \(x \ge 0,x \ne 1\) a) Rút gọn biểu thức \(P\). ĐKXĐ: \(x \ge 0,x \ne 1\) \(\begin{array}{l}P = \dfrac{{3x + \sqrt {9x} - 3}}{{x + \sqrt x - 2}} - \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}} + \dfrac{{\sqrt x - 2}}{{1 - \sqrt x }}\\\;\;\; = \dfrac{{3x + \sqrt {9x} - 3}}{{\left( {x - \sqrt x } \right) + \left( {2\sqrt x - 2} \right)}} - \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}} + \dfrac{{\sqrt x - 2}}{{1 - \sqrt x }}\\\;\;\; = \dfrac{{3x + 3\sqrt x - 3}}{{\left( {\sqrt x + 2} \right).\left( {\sqrt x - 1} \right)}} - \dfrac{{\left( {\sqrt x - 1} \right).\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right).\left( {\sqrt x + 2} \right)}} + \dfrac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}{{ - \left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\\\;\; = \dfrac{{3x + 3\sqrt x - 3 - \left( {x - 1} \right) - \left( {x - 4} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}} = \dfrac{{x + 3\sqrt x + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\\\;\; = \dfrac{{\left( {x + 2\sqrt x } \right) + \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\\\;\; = \dfrac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}} = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}.\end{array}\) Vậy\(P = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}\). b) So sánh \(P\) với \(\sqrt P \) với điều kiện \(\sqrt P \)có nghĩa \(\sqrt P \) có nghĩa \( \Leftrightarrow \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} \ge 0 \Leftrightarrow \sqrt x - 1 > 0\;\;\left( {do\;\;\sqrt x + 1 > 0\;\forall x \ge 0,\;\;x \ne 1} \right)\) \( \Leftrightarrow \sqrt x > 1 \Leftrightarrow x > 1.\) Xét hiệu: \(P - \sqrt P = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} - \sqrt {\dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}} \). \(\begin{array}{l} \Rightarrow P - \sqrt P = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} - \sqrt {\dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}} = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} - \dfrac{{\sqrt {\sqrt x + 1} }}{{\sqrt {\sqrt x - 1} }}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} - \dfrac{{\sqrt {\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)} }}{{{{\left( {\sqrt {\sqrt x - 1} } \right)}^2}}} = \dfrac{{\sqrt x + 1 - \sqrt {x - 1} }}{{\sqrt x - 1}}.\end{array}\) Ta có: \(\sqrt x - \sqrt {x - 1} = \dfrac{{\left( {\sqrt x + \sqrt {x - 1} } \right)\left( {\sqrt x - \sqrt {x - 1} } \right)}}{{\sqrt x + \sqrt {x - 1} }} \)\(\,= \dfrac{{x - \left( {x - 1} \right)}}{{\sqrt x + \sqrt {x - 1} }} = \dfrac{1}{{\sqrt x + \sqrt {x + 1} }} > 0\) Mà có: \(\sqrt x - 1 > 0\) (cmt) \( \Rightarrow P - \sqrt P > 0 \Rightarrow P > \sqrt P \) với mọi \(x > 1.\) \(\)\(\) c) Tìm \(x\) để \(\dfrac{1}{P}\) nguyên. Xét: \(\dfrac{1}{P} = \dfrac{{\sqrt x - 1}}{{\sqrt x + 1}} = \dfrac{{\sqrt x + 1 - 2}}{{\sqrt x + 1}} = 1 - \dfrac{2}{{\sqrt x + 1}}\). Để \(\dfrac{1}{P}\) nguyên thì \(\dfrac{2}{{\sqrt x + 1}}\) nguyên, suy ra \(\sqrt x + 1\) là ước của 2. Mà \(\sqrt x + 1 > \)0 \(\begin{array}{l} \Rightarrow \left( {\sqrt x + 1} \right) \in U\left( 2 \right) \Rightarrow \left( {\sqrt x + 1} \right) = \left\{ {1;\;2} \right\}.\\ \Rightarrow \left[ \begin{array}{l}\sqrt x + 1 = 2\\\sqrt x + 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 1\\\sqrt x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\;\;\left( {ktm} \right)\\x = 0\;\;\;\left( {tm} \right)\end{array} \right..\end{array}\) Vậy với \(x = 0\) thì \(\dfrac{1}{P}\) nguyên. LG bài 3 Lời giải chi tiết: Cho đường thẳng \(\left( {{d_1}} \right) :y = \left( {m - 1} \right)x + 2m + 1\). Tìm \(m\) để đường thẳng \({d_1}\) cắt trục tung tại điểm có tung độ là \( - 3\). Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng \(\left( d \right):y = x + 1\) nằm trên trục hoành. Vì \({d_1}\) cắt trục tung tại điểm có tung độ là \( - 3\), suy ra \(\left( {0; - 3} \right)\) nằm trên đường thẳng \({d_1}\) \( \Rightarrow - 3 = \left( {m - 1} \right).0 + 2m + 1 \Leftrightarrow 2m = - 4 \Leftrightarrow m = - 2\). Với \(m = - 2\) ta có phương trình đường thẳng \(\left( {{d_1}} \right):y = - 3x - 3\). Nhận thấy: \(A\left( {0; - 3} \right),\;B\left( { - 1;\;0} \right)\) nằm trên đồ thị hàm số. Vì hàm số \(\left( {{d_1}} \right):y = - 3x - 3\) là hàm số bậc nhất nên đồ thị của nó có dạng đường thẳng, từ đó ta có đồ thị: Hoành độ giao điểm của \(\left( {{d_1}} \right):y = - 3x - 3\) và \(\left( d \right):y = x + 1\) là nghiệm của phương trình: \(x + 1 = - 3x - 3 \Leftrightarrow 4x = - 4 \) \(\Leftrightarrow x = - 1 \Rightarrow y = x + 1 = - 1 + 1 = 0\). Vậy giao điểm của \(\left( {{d_1}} \right):y = - 3x - 3\) và \(\left( d \right):y = x + 1\) là \(\left( { - 1;0} \right)\). Nhận thấy điểm \(\left( { - 1;0} \right)\) nằm trên trục hoành (do có tung độ bằng 0). Vậy ta có điều cần chứng minh.\(\) LG bài 4 Lời giải chi tiết:
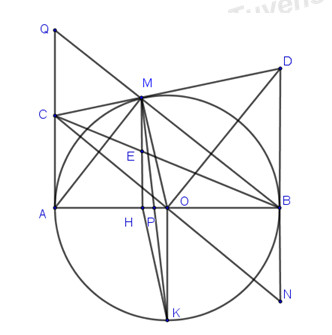
Cho điểm M bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của \(\left( O \right)\) cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N. a) Chứng minh \(DC = DN\). Xét đường tròn \(\left( O \right)\) có MD và BD là tiếp tuyến với B, D là tiếp điểm \( \Rightarrow MD = DB\)(tính chất tiếp tuyến) Xét tam giác MOD và tam giác BOD có: \(MD = BD\) (cmt) \(MO = OB\) (cùng là bán kính đường tròn) OD chung \( \Rightarrow \Delta MOD = \Delta BOD \Rightarrow \angle MDO = \angle BDO \Rightarrow OD\) là phân giác \(\angle MDB\). Xét tam giác CDN có: OD là đường cao (do\(OD \bot CN\)) OD là phân giác \(\angle MDB\) Suy ra tam giác CDN cân tại D, suy ra \(CD = ND\) (đpcm)\(\) \(\) \(\) \(\) \(\) \(\) b) Chứng minh AC là tiếp tuyến của đường tròn tâm O. Xét tam giác CND cân tại D có OD là đường cao ứng với đỉnh D, suy ra OD đồng thời là trung trực ứng với cạnh CN, suy ra \(CO = ON\) Xét tam giác COA và tam giác BON có: \(CO = ON\) (cmt) \(OA = OB\) (do cùng là bán kính) \(\angle COA = \angle BON\) (hai góc đối đỉnh) \( \Rightarrow \Delta COA = \Delta BON \Rightarrow \angle CAO = \angle NBO = {90^o}\) Xét đường tròn tâm O có AC vuông góc với AO, AO là bán kính đường tròn, suy ra AC là tiếp tuyến của đường tròn (đpcm).\(\) c) Gọi H là chân đường vuông góc kẻ từ M xuống AB, I là trung điểm MH. Chứng minh B, C, I thẳng hàng. Kéo dài BM cắt AC tại Q, BC cắt MH tại E Xét tam giác BMD có \(DM = DB\;\;\left( {cmt} \right) \Rightarrow \angle DMB = \angle DBM\) Ta có: \(AB \bot AQ,\;\;AB \bot DN \Rightarrow AQ//DN.\) Mà có \(\angle CQM = \angle MBD\) (so le trong) Lại có: \(\angle QMC = \angle DMB\) (đối đỉnh) \( \Rightarrow \angle CQM = \angle QMC\), suy ra tam giác MCQ cân tại C, suy ra \(QC = MC\) Chứng minh tương tự như ở câu a ta có \(AC = MC\) (do tính chất tiếp tuyến) Suy ra \(QC = AC \Rightarrow QC = \dfrac{1}{2}QA\). Xét tam giác BQC có ME song song với QC (cùng vuông góc với AB) \( \Rightarrow \dfrac{{ME}}{{QC}} = \dfrac{{BM}}{{BQ}}\) (định lí Ta-lét) Chứng minh tương tự có \(\dfrac{{MH}}{{AQ}} = \dfrac{{BM}}{{BQ}}\) Suy ra \(\dfrac{{ME}}{{QC}} = \dfrac{{MH}}{{AQ}}\). Mà có \(QC = \dfrac{1}{2}QA\) suy ra \(ME = \dfrac{1}{2}MH\), suy ra E là trung điểm của MH. Mà theo đề bài có I là trung điểm của MH, suy ra I trùng với E, suy ra B, C, I thẳng hàng (đpcm). d) Qua O kẻ đường vuông góc với AB, cắt \(\left( O \right)\) tại K (K và M nằm khác phía với đường thẳng AB). Tìm vị trí của M để diện tích tam giác MHK lớn nhất. Gọi P là giao điểm của MK và AB. Không mất tính tổng quát, ta chọn bán kính đường tròn bằng 1, giả sử độ dài đoạn \(OH = a\;\;\left( {0 < a < 1} \right).\) \( \Rightarrow MH = \sqrt {O{M^2} - O{H^2}} = \sqrt {1 - {a^2}} \). Có MH song song với OK (do cùng vuông góc với AB) \( \Rightarrow \dfrac{{PH}}{{PO}} = \dfrac{{MH}}{{OK}} = \dfrac{{\sqrt {1 - {a^2}} }}{1} \Rightarrow PH = \sqrt {1 - {a^2}} .OP.\) Ta có hệ: \(\left\{ \begin{array}{l}\dfrac{{PH}}{{PO}} = \sqrt {1 - {a^2}} \\PH + PO = OH = a\end{array} \right. \\\Rightarrow \left\{ \begin{array}{l}PO = \dfrac{{PH}}{{\sqrt {1 - {a^2}} }}\\PH + \dfrac{{PH}}{{\sqrt {1 - {a^2}} }} = a\end{array} \right.\\ \Rightarrow PH = \dfrac{{a.\sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}} + 1}}\\ \Rightarrow OP = \dfrac{a}{{\sqrt {1 - {a^2}} + 1}}.\) Ta có: \(\begin{array}{l}{S_{MHK}} = {S_{MHP}} + {S_{PKH}} = \dfrac{1}{2}MH.HP + \dfrac{1}{2}OK.HP\\ = \dfrac{1}{2}\left( {\sqrt {1 - {a^2}} .\dfrac{{a\sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}} + 1}} + 1.\dfrac{{a\sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}} + 1}}} \right)\\ = \dfrac{1}{2}a\sqrt {1 - {a^2}} .\dfrac{{\sqrt {1 - {a^2}} + 1}}{{\sqrt {1 - {a^2}} + 1}} = \dfrac{1}{2}a\sqrt {1 - {a^2}} .\end{array}\) Áp dụng bất đẳng thức Cosi ta có: \(a\sqrt {1 - {a^2}} \le \dfrac{{{a^2} + 1 - {a^2}}}{2} = \dfrac{1}{2}\) Dấu “=” xảy ra \( \Leftrightarrow a = \sqrt {1 - {a^2}} \Rightarrow a = \dfrac{1}{{\sqrt 2 }} \) \(\Rightarrow \cos \angle MOH = \dfrac{{OH}}{R} = \dfrac{1}{{\sqrt 2 }} \Rightarrow \angle MOH = {45^o}\). Vậy M là điểm nằm trên đường tròn sao cho \(\angle MOH = {45^o}\) là điểm thỏa mãn yêu cầu bài toán. LG bài 5 Lời giải chi tiết: Cho các số thực dương \(x,\;y,\;z\) thỏa mãn \(x + 2y + 3z \ge 20\). Tìm giá trị nhỏ nhất của biểu thức : \(A = x + y + z + \dfrac{3}{x} + \dfrac{9}{{2y}} + \dfrac{4}{z}\). Ta có: \(A = x + y + z + \dfrac{3}{x} + \dfrac{9}{{2y}} + \dfrac{4}{z}\)\(\, = \dfrac{1}{4}x + \left( {\dfrac{3}{4}x + \dfrac{3}{x}} \right) + \dfrac{1}{2}y + \left( {\dfrac{1}{2}y + \dfrac{9}{{2y}}} \right) + \dfrac{3}{4}z + \left( {\dfrac{1}{4}z + \dfrac{4}{z}} \right)\) Áp dụng bất đẳng thức Cosi cho các số dương ta có: \(\begin{array}{l} + )\dfrac{3}{4}x + \dfrac{3}{x} \ge 2\sqrt {\dfrac{3}{4}x.\dfrac{3}{x}} = 3\\ + )\dfrac{1}{2}y + \dfrac{9}{{2y}} \ge 2\sqrt {\dfrac{1}{2}y.\dfrac{9}{{2y}}} = 3\\ + )\dfrac{1}{4}z + \dfrac{4}{z} \ge 2\sqrt {\dfrac{1}{4}z.\dfrac{4}{z}} = 2\end{array}\) \( \Rightarrow A \ge \dfrac{1}{4}\left( {x + 2y + 3z} \right) + 3 + 3 + 2 = \dfrac{{20}}{4} + 3 + 3 + 2 = 13\). Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{4}x = \dfrac{3}{x}\\\dfrac{1}{2}y = \dfrac{9}{{2y}}\\\dfrac{1}{4}z = \dfrac{4}{z}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\\z = 4\end{array} \right.\).
|