Đề số 1 - Đề kiểm tra học kì 1 - Toán 7Đáp án và lời giải chi tiết Đề số 1 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 7 Đề bài Bài 1 (2 điểm) a) \(\sqrt {25} - \sqrt {\dfrac{{49}}{4}} + \sqrt {0,25} \) b) \(\left( { - \dfrac{{25}}{{27}} - \dfrac{{31}}{{42}}} \right) - \left( {\dfrac{{ - 7}}{{27}} - \dfrac{3}{{42}}} \right)\) c) \(\dfrac{{10\dfrac{3}{{10}} - (9,5 - 0,25.18):0,5}}{{1\dfrac{1}{5} - 1\dfrac{1}{2}}}\) d) \(\dfrac{3}{{49}}.\dfrac{{19}}{2} - \dfrac{3}{{49}}.\dfrac{5}{2} - {\left( {\dfrac{1}{{20}} - \dfrac{1}{4}} \right)^2}.\left( {\dfrac{{ - 1}}{2} - \dfrac{{193}}{{14}}} \right)\) Bài 2 (2 điểm) 1) Tìm x biết: a) \(\left| {\dfrac{1}{2}x - \dfrac{1}{6}} \right| = \dfrac{1}{3}\) b) \({\left( {4{{\rm{x}}^2} - 3} \right)^3} + 8 = 0\) 2) Vẽ đồ thị hàm số \(y = \dfrac{{ - 1}}{2}x\). Từ đó chứng minh 3 điểm A(2; -1), B(-12; -6) và C(-2; 1) không thẳng hàng. Bài 3 (1,5 điểm) Có ba máy bơm cùng bơm nước vào ba bể có thể tích bằng nhau (lúc đầu các bể đều không có nước). Mỗi giờ máy thứ nhất, máy thứ hai, máy thứ ba bơm được lần lượt là 6m3, 10m3, 9m3. Thời gian bơm đầy bể của máy thứ hai ít hơn máy thứ nhấtlà 2 giờ. Tính thời gian của từng máy để bơm đầy bể. Bài 4 (3,5 điểm) Cho tam giác ABC có AB < AC, tia phân giác của góc A cắt cạnh BC tại I. Trên cạnh AC lấy điểm D sao cho AD = AB. a) Chứng minh rằng BI = ID. b) Tia DI cắt tia AB tại E. Chứng minh rằng \(\Delta IBE = \Delta I{\rm{D}}C\). c) Chứng minh BD // EC. d) Cho \(\angle ABC = 2\angle ACB.\) Chứng minh rằng AB + BI = AC. Bài 5 (1 điểm) a) Cho các số a, b, c, x, y, z thỏa mãn a + b + c = a2 + b2 + c2 = 1 và \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}\) (các tỉ số đều có nghĩa). Chứng minh x2 + y2 + z2 = (x + y + z)2. b) (Dành riêng cho lớp 7A) Cho tam giác ABC có AB = 2 cm, BC = 4 cm và \(\widehat {ABC}\) = 600. Trên tia đối của tia BC lấy điểm D sao cho BD = BC, trên tia đối của tia BA lấy điểm E sao cho BE = BA. Tính diện tích tứ giác ACED. Lời giải chi tiết Bài 1: \(\begin{array}{l}a)\;\sqrt {25} - \sqrt {\dfrac{{49}}{4}} + \sqrt {0,25} \\ = \sqrt {{5^2}} - \sqrt {{{\left( {\dfrac{7}{2}} \right)}^2}} + \sqrt {0,{5^2}} \\ = 5 - \dfrac{7}{2} + 0,5\\ = 5 - 3,5 + 0,5 = 2.\end{array}\) \(\begin{array}{l}b)\;\left( { - \dfrac{{25}}{{27}} - \dfrac{{31}}{{42}}} \right) - \left( {\dfrac{{ - 7}}{{27}} - \dfrac{3}{{42}}} \right)\\ = - \dfrac{{25}}{{27}} - \dfrac{{31}}{{42}} + \dfrac{7}{{27}} + \dfrac{3}{{42}}\\ = \left( {\dfrac{7}{{27}} - \dfrac{{25}}{{27}}} \right) + \left( {\dfrac{3}{{42}} - \dfrac{{31}}{{42}}} \right)\\ = - \dfrac{{18}}{{27}} - \dfrac{{28}}{{42}} = - \dfrac{2}{3} - \dfrac{2}{3} = \dfrac{{ - 4}}{3}\end{array}\) \(\begin{array}{l}c)\;\dfrac{{10\dfrac{3}{{10}} - (9,5 - 0,25.18):0,5}}{{1\dfrac{1}{5} - 1\dfrac{1}{2}}}\\ = \dfrac{{\dfrac{{103}}{{10}} - (\dfrac{{19}}{2} - \dfrac{1}{4}.18):\dfrac{1}{2}}}{{\dfrac{6}{5} - \dfrac{3}{2}}} \\= \dfrac{{\dfrac{{103}}{{10}} - (\dfrac{{19}}{2} - \dfrac{9}{2}).2}}{{\dfrac{{6.2}}{{5.2}} - \dfrac{{3.5}}{{5.2}}}}\\ = \dfrac{{\dfrac{{103}}{{10}} - \dfrac{{10}}{2}.2}}{{\dfrac{{12}}{{10}} - \dfrac{{15}}{{10}}}} = \dfrac{{\dfrac{{103}}{{10}} - 10}}{{\dfrac{{ - 3}}{{10}}}}\\ = \dfrac{{\dfrac{{103}}{{10}} - \dfrac{{100}}{{10}}}}{{\dfrac{{ - 3}}{{10}}}} = \dfrac{{\dfrac{3}{{10}}}}{{\dfrac{{ - 3}}{{10}}}} = - 1\end{array}\) \(\begin{array}{l}d)\;\;\dfrac{3}{{49}}.\dfrac{{19}}{2} - \dfrac{3}{{49}}.\dfrac{5}{2} - {\left( {\dfrac{1}{{20}} - \dfrac{1}{4}} \right)^2}.\left( {\dfrac{{ - 1}}{2} - \dfrac{{193}}{{14}}} \right)\\ = \dfrac{3}{{49}}.\left( {\dfrac{{19}}{2} - \dfrac{5}{2}} \right) - {\left( {\dfrac{1}{{20}} - \dfrac{{1.5}}{{4.5}}} \right)^2}.\left( {\dfrac{{( - 1).7}}{{2.7}} - \dfrac{{193}}{{14}}} \right)\\ = \dfrac{3}{{49}}.\dfrac{{14}}{2} - {\left( {\dfrac{1}{{20}} - \dfrac{5}{{20}}} \right)^2}.\left( {\dfrac{{ - 7}}{{14}} - \dfrac{{193}}{{14}}} \right)\\ = \dfrac{3}{7} - {\left( {\dfrac{{ - 4}}{{20}}} \right)^2}.\left( {\dfrac{{ - 200}}{{14}}} \right)\\ = \dfrac{3}{7} - {\left( {\dfrac{{ - 1}}{5}} \right)^2}.\left( {\dfrac{{ - 100}}{7}} \right)\\ = \dfrac{3}{7} - \dfrac{1}{{25}}.\dfrac{{( - 100)}}{7}\\ = \dfrac{3}{7} + \dfrac{4}{7} = \dfrac{7}{7} = 1\end{array}\) Bài 2: 1) a) - Nếu \(\dfrac{1}{2}x - \dfrac{1}{6} \ge 0\) tức \(x \ge \dfrac{1}{3}\) thì \(\left| {\dfrac{1}{2}x - \dfrac{1}{6}} \right| = \dfrac{1}{2}x - \dfrac{1}{6}\) Ta có phương trình \( \Leftrightarrow \dfrac{1}{2}x - \dfrac{1}{6} = \dfrac{1}{3}\) \(\Leftrightarrow \dfrac{1}{2}x = \dfrac{1}{3} + \dfrac{1}{6} \) \(\Leftrightarrow \dfrac{1}{2}x = \dfrac{1}{2} \) \(\Leftrightarrow x = 1\;\;\;\;\left( {tmdk\;\;x \ge \dfrac{1}{3}} \right)\) - Nếu \(\dfrac{1}{2}x - \dfrac{1}{6} < 0\) tức là x <\(\dfrac{1}{3}\)thì\(\left| {\dfrac{1}{2}x - \dfrac{1}{6}} \right| = - \left( {\dfrac{1}{2}x - \dfrac{1}{6}} \right) = \dfrac{1}{6} - \dfrac{1}{2}x\) Ta có phương trình \( \Leftrightarrow \dfrac{1}{6} - \dfrac{1}{2}x = \dfrac{1}{3}\) \(\Leftrightarrow \dfrac{1}{2}x = \dfrac{1}{6} - \dfrac{1}{3}\) \(\Leftrightarrow \dfrac{1}{2}x = \dfrac{{ - 1}}{6} \) \(\Leftrightarrow x = \dfrac{{ - 1}}{3}\;\;\;\left( {tmdk\;\;x < \dfrac{1}{3}} \right)\) Vậy x = 1 hoặc\(x = - \dfrac{1}{3}.\) b) \(\begin{array}{l}\;\;\;\;{\left( {4{x^2} - 3} \right)^3} + 8 = 0 \Leftrightarrow {\left( {4{x^2} - 3} \right)^3} = - 8\\ \Leftrightarrow 4{x^2} - 3 = - 2 \Leftrightarrow 4{x^2} = 1\\ \Leftrightarrow {x^2} = \dfrac{1}{4} \Leftrightarrow \left| x \right| = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = - \dfrac{1}{2}\end{array} \right..\end{array}\)\(\) Vậy \(x = \dfrac{{ - 1}}{2}\) hoặc \(x = \dfrac{1}{2}\). 2) Vẽ đồ thị hàm số \(y = - \dfrac{1}{2}x\) . - Khi \(x = - 2\)thì\(y = \dfrac{{ - 1}}{2}.\left( { - 2} \right) = 1\). Vậy điểm \(C\left( { - 2;\;1} \right)\)thuộc đồ thị của hàm số . Đồ thị của hàm số này là đường thẳng OC trong hình vẽ bên. - Xét điểm A, B thấy điểm C thuộc đồ thị còn điểm B không thuộc đồ thị , thật vậy: + Khi x = \( - 12\) thì \(y = \dfrac{{ - 1}}{2}.( - 12) = 6 \ne - 6\) nên điểm B(\( - 12;\; - 6\)) không thuộc đồ thị . + Khi \(x = 2\) thì \(y = \dfrac{{ - 1}}{2}.2 = - 1\) nên điểm \(A\left( {2; - 1} \right)\) thuộc đồ thị . Điểm A, C thuộc đồ thị còn điểm B không thuộc đồ thị nên 3 điểm A, B, C không thẳng hàng. (đpcm) Bài 3: Gọi thời gian của từng máy để bơm đầy bể theo thứ tự là \(x,\;y,\;z\) (giờ) \(\left( {x,\;y,\;z > 0} \right).\) Vì thể tích 3 bể như nhau, nên thời gian của từng máy để bơm đầy b và thể tích nước bơm được mỗi giờ của mỗi máy là 2 đại lượng tỉ lệ nghịch. Theo đề bài ta có: 6.x = 10.y = 9.z (1) và x – y = 2 (2) Từ (1) ta có: \(\dfrac{{6{\rm{x}}}}{{90}} = \dfrac{{10y}}{{90}} = \dfrac{{9{\rm{z}}}}{{90}}\) (90 làBCNN(6; 10; 9)\( \Rightarrow \dfrac{x}{{15}} = \dfrac{y}{9} = \dfrac{z}{{10}}\) (3) Theo tính chất của dãy tỉ số bằng nhau, từ (3) và (2) ta có:\(\dfrac{x}{{15}} = \dfrac{y}{9} = \dfrac{z}{{10}} = \dfrac{{x - y}}{{15 - 9}} = \dfrac{2}{6} = \dfrac{1}{3}\) \( \Rightarrow x = \dfrac{{15}}{3} = 5\)giờ, \(y = \dfrac{9}{3} = 3\)giờ và\(z = \dfrac{{10}}{3}\)giờ = 3 giờ 20 phút. Vậy thời gian của từng máy để bơm đầy bể lần lượt là 5 giờ, 3 giờ và 3 giờ 20 phút. Bài 4:
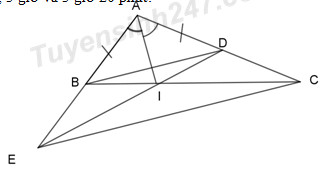
a) Xét tam giác ABI và tam giác ADI ta có: \(\angle BAI = \angle DAI\) (theo giả thiết) \(AB = A{\rm{D}}\) (theo giả thiết) AI: chung \( \Rightarrow \Delta ABI = \Delta A{\rm{D}}I\;\;(c - g - c)\) \( \Rightarrow BI = ID\) (2 cạnh tương ứng) (đpcm) b) Vì\(\Delta ABI = \Delta A{\rm{D}}I\;(c - g - c)\) nên: \(\angle ABI = \angle A{\rm{D}}I\) (2 góc tương ứng) (1) Mà: \(\angle ABE = \angle A{\rm{D}}C = {180^0}\) (2 góc bẹt) (2) Từ (1) và (2) ta có: \(\angle ABE - \angle ABI = \angle A{\rm{D}}C - \angle ADI \Leftrightarrow \angle IBE = \angle IDC\) Xét \(\Delta IBE\)và\(\Delta IDC\) ta có: \(\angle IBE = \angle I{\rm{D}}C\) (chứng minh trên) \(\angle BIE = \angle DIC\) (2 góc đối đỉnh) \(BI = I{\rm{D}}\) (chứng minh trên) \(\)\( \Rightarrow \Delta IBE = \Delta I{\rm{D}}C\;(g - c - g)\) (đpcm) c) Ta có: BI = ID (chứng minh trên) \( \Rightarrow \Delta BI{\rm{D}}\) cân tại \(I \Rightarrow \angle IBD = \angle IDB\) (tính chất của tam giác cân) (1) Ta lại có: \(\Delta IBE = \Delta I{\rm{D}}C\;(g - c - g)\) (chứng minh trên) \( \Rightarrow IE = IC\) (2 cạnh tương ứng) \( \Rightarrow \Delta IEC\) cân tại I \( \Rightarrow \angle IEC = \angle ICE\) (tính chất của tam giác cân) (2) Xét 2 tam giác \(\Delta IEC\)và\(\Delta IBD\) ta có: \(\angle BID = \angle EIC\) (2 góc đối đỉnh) \(\angle IBD + \angle IDB + \angle BID = \angle IEC + \angle IC{\rm{E}} + \angle EIC = {180^0}\) (Tổng 3 góc của một tam giác bằng 1800) (3) Từ (1), (2) và (3) ta có: \(2\angle I{\rm{D}}B + \angle BI{\rm{D}} = 2\angle IEC + \angle EIC\) \( \Rightarrow \angle I{\rm{D}}B = \angle IEC\;\;hay\;\;\angle E{\rm{D}}B = \angle DEC\) (cặp góc so le trong bằng nhau) \( \Rightarrow B{\rm{D}}\parallel EC\) (đpcm) d)Ta có \(\Delta IBE = \Delta I{\rm{D}}C\;(g - c - g)\) (chứng minh trên) \( \Rightarrow \angle BEI = \angle DCI\) (2 góc tương ứng) Lại có: \(\angle BIE = \angle DIC\) (2 góc đối đỉnh) \( \Rightarrow \angle BEI + \angle BIE = \angle DCI + \angle DIC\) (*) Xét tam giác BIE ta có: \(\angle ABC = \angle BIE + \angle BEI\) (góc ngoài của 1 tam giác bằng tổng 2 góc trong không kề với nó) (**) Từ (*) và (**) ta có: \(\angle ABC = \angle DCI + \angle DIC\) hay \(\angle ABC = \angle ACB + \angle DIC\) Theo giả thiết, ta có: \(\)\(\angle ABC = 2\angle ACB\) \( \Rightarrow \angle DCI = \angle DIC \Rightarrow \Delta DIC\) cân tại \(D \Rightarrow DI = DC\). Vì BI = ID (chứng minh trên) nên BI = DC. \( \Rightarrow \) AC = AD + DC = AB + BI (đpcm) Bài 5: a) Theo tính chất dãy tỉ số bằng nhau ta có: \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x + y + z}}{{a + b + c}} \)\(\,= \dfrac{{x + y + z}}{1} = x + y + z\) (Theo giả thiết a + b + c = 1) \(\)\( \Rightarrow {\left( {\dfrac{x}{a}} \right)^2} = {\left( {\dfrac{y}{b}} \right)^2} = {\left( {\dfrac{z}{c}} \right)^2} = {\left( {x + y + z} \right)^2}\) (1) Theo tính chất dãy tỉ số bằng nhau, ta lại có: \({\left( {\dfrac{x}{a}} \right)^2} = {\left( {\dfrac{y}{b}} \right)^2} = {\left( {\dfrac{z}{c}} \right)^2}\)\(\; = \dfrac{{{x^2} + {y^2} + {z^2}}}{{{a^2} + {b^2} + {c^2}}} = \dfrac{{{x^2} + {y^2} + {z^2}}}{1} = {x^2} + {y^2} + {z^2}\)(Theo giả thiết\({a^2} + {b^2} + {c^2} = 1\)) (2) Từ (1) và (2) ta có: \({x^2} + {y^2} + {z^2} = {\left( {x + y + z} \right)^2}\;\;\;\left( {dpcm} \right)\) b) Xét\(\Delta ABC\) và \(\Delta EB{\rm{D}}\) ta có: AB = EB (theo gt) BD = BC (theo gt) \(\angle ABC = \angle EB{\rm{D}}\) (cặp góc đối đỉnh bằng nhau) \( \Rightarrow \Delta ABC = \Delta EB{\rm{D}}\left( {c - g - c} \right)\) Chứng minh tương tự ta có: \(\Delta AB{\rm{D}} = \Delta EBC\;\left( {c - g - c} \right)\) \( \Rightarrow {S_{\Delta ABC}} + {S_{\Delta AB{\rm{D}}}} = {S_{\Delta EB{\rm{D}}}} + {S_{\Delta EBC}}\)\( \Rightarrow {S_{\Delta E{\rm{D}}C}} = {S_{\Delta AC{\rm{D}}}} = \dfrac{1}{2}{S_{AC{\rm{ED}}}}\) Kẻ đường cao AH của tam giác ACD (\(H \in DC\)) Xét tam giác vuông AHB ta có: \(\angle BAH + \angle ABH = {90^0} \Leftrightarrow \angle BAH + {60^0} = {90^0} \Leftrightarrow \angle BAH = {30^0}\) \( \Rightarrow BH = \dfrac{1}{2}AB = \dfrac{1}{2}.2 = 1\;cm\) (Tam giác vuông có một góc bằng 30000000 thì cạnh đối diện góc đó bằng nửa cạnh huyền) Áp dụng định lý Pitago vào tam giác vuông AHB, ta có: \(A{H^2} + B{H^2} = A{B^2} \Leftrightarrow A{H^2} + {1^2} = {2^2}\) \(\Leftrightarrow A{H^2} = 4 - 1 = 3 \Leftrightarrow AH = \sqrt 3 \;cm\) Vậy diện tích tứ giác ACED là: \({S_{AC{\rm{ED}}}} = 2.{S_{\Delta AC{\rm{D}}}} \)\(\,= 2.\dfrac{1}{2}.AH.DC = AH.2BC = \sqrt 3 .2.4 = 8\sqrt 3 \;c{m^2}\) HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|