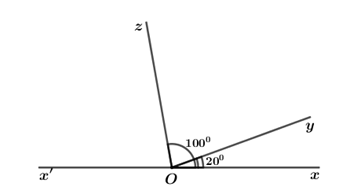
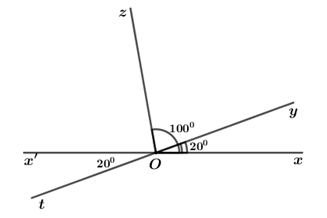
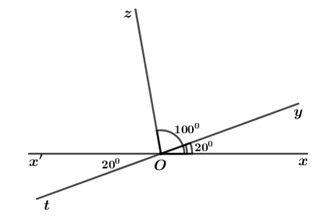
Đề kiểm tra giữa kì II Toán 6 - Đề số 2 có lời giải chi tiết

Đề bài

Câu 1 (3 điểm): Tính giá trị của các biểu thức sau:

a) $A = \frac{{ - 1}}{4} \cdot \frac{{152}}{{11}} + \frac{1}{4} \cdot \frac{{ - 68}}{{11}}$

b) $B = \frac{{ - 11}}{{19}} \cdot \frac{4}{{13}} + \frac{{ - 11}}{{13}} \cdot \frac{{15}}{{19}} + \frac{{11}}{{13}}$

c) $C = \left( { - \frac{9}{{25}}} \right) \cdot \frac{{53}}{5} - {\left( {\frac{{ - 3}}{5}} \right)^2} \cdot \frac{{22}}{5}$                                      

Câu 2 (2 điểm): Tìm $x$ biết:

a)  $\frac{3}{4} + \frac{1}{4}:x =  - 3$

b) $\left| {2x - 7} \right| - \left| { - \frac{3}{2}} \right| = 7$  $\frac{3}{4} + \frac{1}{4}:x =  - 3$                                                         

Câu 3 (2,5 điểm): Tìm một phân số có mẫu số bằng $15$, biết rằng nếu trừ đi ở tử số $10$ đơn vị và cộng thêm vào mẫu số $10$ đơn vị thì ta được phân số mới có giá trị gấp $\frac{8}{5}$ lần phân số ban đầu.

Câu 4 (2,5 điểm): Trên đường thẳng $xx'$ lấy điểm $O$. Trên cùng một nửa mặt phẳng có bờ là $xx'$, vẽ hai tia $Oy$ và $Oz$ sao cho số đo góc $xOy$ bằng ${20^0}$, số đo góc $xOz$ bằng ${100^0}$.

a)  Tính số đo góc $yOz$.

b) Chứng minh rằng: Tia $Oz$ là tia phân giác của góc $yOx'$.

c)  Vẽ tia $Ot$ sao cho số đo góc $tOx'$ bằng ${20^0}$. Hỏi tia $Oy$ và tia $Ot$ có phải là hai tia đối nhau không?

Lời giải chi tiết

Câu 1 (VD)

Phương pháp:

Sử dụng phương pháp đặt thừa số chung. Sau đó, áp dụng các quy tắc cộng và nhân phân số.

Cách giải:

Tính giá trị của các biểu thức sau:

a) $A = \frac{{ - 1}}{4} \cdot \frac{{152}}{{11}} + \frac{1}{4} \cdot \frac{{ - 68}}{{11}}$

$\begin{array}{l}A = \frac{{ - 1}}{4} \cdot \frac{{152}}{{11}} + \frac{1}{4} \cdot \frac{{ - 68}}{{11}}\\\,\,\,\,\, = \frac{{ - 1}}{4} \cdot \frac{{152}}{{11}} + \frac{{ - 1}}{4} \cdot \frac{{68}}{{11}}\\\,\,\,\,\, = \frac{{ - 1}}{4} \cdot \left( {\frac{{152}}{{11}} + \frac{{68}}{{11}}} \right)\\\,\,\,\,\, = \frac{{ - 1}}{4} \cdot 20\\\,\,\,\,\, =  - 5\end{array}$

b) $B = \frac{{ - 11}}{{19}} \cdot \frac{4}{{13}} + \frac{{ - 11}}{{13}} \cdot \frac{{15}}{{19}} + \frac{{11}}{{13}}$

$\begin{array}{l}B = \frac{{ - 11}}{{19}} \cdot \frac{4}{{13}} + \frac{{ - 11}}{{13}} \cdot \frac{{15}}{{19}} + \frac{{11}}{{13}}\\\,\,\,\,\, = \frac{{ - 11}}{{13}} \cdot \frac{4}{{19}} + \frac{{ - 11}}{{13}} \cdot \frac{{15}}{{19}} + \frac{{11}}{{13}} \cdot 1\\\,\,\,\,\, = \frac{{ - 11}}{{13}} \cdot \left( {\frac{4}{{19}} + \frac{{15}}{{19}} - 1} \right)\\\,\,\,\,\, = \frac{{ - 11}}{{13}} \cdot 0\\\,\,\,\,\, = 0\end{array}$

Câu 2 (VD)

Phương pháp:

Giải bài toán ngược để tìm $x$.

Cách giải:

Tìm $x$ biết:

a) $\frac{3}{4} + \frac{1}{4}:x =  - 3$

$\begin{array}{l}\frac{3}{4} + \frac{1}{4}:x =  - 3\\\frac{1}{4}:x =  - 3 - \frac{3}{4}\\\frac{1}{4}:x = \frac{{ - 15}}{4}\\x = \frac{1}{4}:\frac{{ - 15}}{4}\\x =  - \frac{1}{{15}}\end{array}$

Vậy $x =  - \frac{1}{{15}}$

b) $\left| {2x - 7} \right| - \left| { - \frac{3}{2}} \right| = 7$

$\begin{array}{l}\left| {2x - 7} \right| - \left| { - \frac{3}{2}} \right| = 7\\\left| {2x - 7} \right| - \frac{3}{2} = 7\\\left| {2x - 7} \right| = 7 + \frac{3}{2}\\\left| {2x - 7} \right| = \frac{{17}}{2}\end{array}$

Trường hợp 1:

$\begin{array}{l}2x - 7 = \frac{{17}}{2}\\2x = \frac{{17}}{2} + 7\\2x = \frac{{31}}{2}\\x = \frac{{31}}{4}\end{array}$

Trường hợp 2:

$\begin{array}{l}2x - 7 =  - \frac{{17}}{2}\\2x =  - \frac{{17}}{2} + 7\\2x =  - \frac{3}{2}\\x =  - \frac{3}{4}\end{array}$

Vậy $x \in \left\{ { - \frac{3}{4};\,\,\frac{{31}}{3}} \right\}$.

Câu 3 (VD)

Phương pháp:

Gọi phân số ban đầu là $\frac{x}{{15}}\,\,\left( {x \in \mathbb{Z}} \right)$.

Áp dụng định nghĩa: Hai phân số $\frac{a}{b}$ và $\frac{c}{d}$ gọi là bằng nhau nếu $a.d = b.c$.

Cách giải:

Tìm một phân số có mẫu số bằng $15$, biết rằng nếu trừ đi ở tử số $10$ đơn vị và cộng thêm vào mẫu số $10$ đơn vị thì ta được phân số mới có giá trị gấp $\frac{8}{5}$ lần phân số ban đầu.

Gọi phân số ban đầu là $\frac{x}{{15}}\,\,\left( {x \in \mathbb{Z}} \right)$.

Theo đề bài, nếu trừ đi ở tử số $10$ đơn vị và cộng thêm vào mẫu số $10$ đơn vị thì phân số mới là $\frac{{x - 10}}{{15 + 10}}$

Phân số mới gấp $\frac{8}{5}$ phân số ban đầu nên ta có phương trình:

$\begin{array}{l}\frac{{x - 10}}{{15 + 10}} = \frac{8}{5} \cdot \frac{x}{{15}}\\\frac{{x - 10}}{{25}} = \frac{{8x}}{{75}}\\25.\frac{{x - 10}}{{25}} = 25.\frac{{8x}}{{75}}\\\frac{{x - 10}}{1} = \frac{{8x}}{3}\\3x - 30 = 8x\\3x - 8x = 30\\ - 5x = 30\\x =  - 6\,\left( {tm} \right)\end{array}$

Vậy phân số cần tìm là $\frac{{ - 6}}{{15}}$.

Câu 4 (VD)

Phương pháp:

a) Chứng minh tia nằm giữa hai tia.

Nếu tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$ thì$\angle xOy + \angle yOz = \angle xOz$

b) $Om$ là tia phân giác của góc $\angle xOy$ nếu thỏa mãn điều kiện sau:

+ Tia $Om$ nằm giữa hai tia $Ox$ và $Oy$

+ $\angle xOm = \angle mOy$

c) Xét hai trường hợp:

+ Tia $Ot$ và $Oz$ nằm trên cùng một nửa mặt phẳng có bờ chứa tia $Ox'$.

+ Tia $Ot$ và $Oz$ nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia $Ox'$.

Cách giải:

a) Tính số đo góc $yOz$.

Trên cùng một nửa mặt phẳng có bờ chứa tia $Ox$, có $\angle xOy < \angle xOz$ (vì ${20^0} < {100^0}$) nên tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$.

Vì tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$ nên ta có:

$\begin{array}{l}\angle xOy + \angle yOz = \angle xOz\\\angle yOz = \angle xOz - \angle xOy\\\angle yOz = {100^0} - {20^0}\\\angle yOz = {80^0}\end{array}$

Vậy $\angle yOz = {80^0}$.

b) Chứng minh rằng: Tia $Oz$ là tia phân giác của góc $yOx'$.

Vì điểm $O$ nằm trên đường thẳng $xx'$ nên $Ox$ và $Ox'$ là hai tia đối nhau.

Vì $Ox$ và $Ox'$ là hai tia đối nhau nên $\angle xOy$ và $\angle yOx'$ là hai góc kề bù. Ta có:

$\begin{array}{l}\angle xOy + \angle yOx' = \angle xOx'\\\angle yOx' = \angle xOx' - \angle xOy\\\angle zOx' = {180^0} - {20^0}\\\angle zOx' = {160^0}\end{array}$

Vì $Ox$ và $Ox'$ là hai tia đối nhau nên $\angle xOz$ và $\angle zOx'$ là hai góc kề bù. Ta có:

$\begin{array}{l}\angle xOz + \angle zOx' = {180^0}\\\angle zOx' = {180^0} - \angle xOz\\\angle zOx' = {180^0} - {100^0}\\\angle zOx'\, = {80^0}\end{array}$

Ta có:

+ Tia $Oz$ nằm giữa hai tia $Ox'$ và $Oy$.

+ $\angle zOx' = \angle yOz\,\left( { = {{80}^0}} \right)$

Suy ra, tia $Oz$ là tia phân giác của góc $yOx'$(định nghĩa)

c) Vẽ tia $Ot$ sao cho số đo góc $tOx'$ bằng ${20^0}$. Hỏi tia $Oy$ và tia $Ot$ có phải là hai tia đối nhau không?

Trường hợp 1: Tia $Ot$ và $Oz$ nằm trên cùng một nửa mặt phẳng có bờ chứa tia $Ox'$.

Trên cùng một nửa mặt phẳng có bờ chứa tia $Ox'$, có $\angle x'Ot < \angle x'Oz$ (vì ${20^0} < {80^0}$). Do đó, tia $Ot$ nằm giữa hai tia $Ox'$ và $Oz$.

Vì tia $Ot$ nằm giữa hai tia $Ox'$ và $Oz$ nên:

$\begin{array}{l}\angle x'Ot + \angle tOz = \angle x'Oz\\\angle tOz = \angle x'Oz - \angle x'Ot\\\angle tOz = {80^0} - {20^0}\\\angle tOz = {60^0}\end{array}$

Ta có:

+ Tia $Ot$ nằm giữa hai tia $Ox'$ và $Oz$ nên hai tia $Ox'$ và $Ot$ nằm trên cùng một nửa mặt phẳng có bờ chứa tia $Oz$.

+ Tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$ nên hai tia $Ox$ và $Oy$ nằm trên cùng một nửa mặt phẳng có bờ chứa tia $Oz$.

+ $Ox$ và $Ox'$ là hai tia đối nhau nên $Ox$ và $Ox'$ nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia $Oz$.

Suy ra, hai tia $Oy$ và $Ot$ nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia $Oz$.

Suy ra, tia $Oz$ nằm giữa hai tia $Oy$ và $Ot$. Khi đó, ta có:

$\begin{array}{l}\angle tOz + \angle zOy = \angle tOy\\\angle tOy = {60^0} + {80^0}\\\angle tOy = {140^0} \ne {180^0}\end{array}$

$\Rightarrow \angle tOy = {140^0} \ne {180^0}$

$\Rightarrow$ Tia $Oy$ và tia $Ot$ không phải là hai tia đối nhau.

Trường hợp 2: Tia $Ot$ và $Oz$ nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia $Ox'$.

Vì tia $Ot$ và $Oz$ nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia $Ox'$ nên tia $Ox'$ nằm giữa hai tia $Oz$ và $Ot$. Ta có:

$\begin{array}{l}\angle tOx' + \angle x'Oz = \angle tOz\\\angle tOz = {20^0} + {80^0}\\\angle tOz = {100^0}\end{array}$

Ta có:

+ Tia $Ox'$ nằm giữa hai tia $Ot$ và $Oz$ nên hai tia $Ox'$ và $Ot$ nằm trên cùng một nửa mặt phẳng có bờ chứa tia $Oz$.

+ Tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$ nên hai tia $Ox$ và $Oy$ nằm trên cùng một nửa mặt phẳng có bờ chứa tia $Oz$.

+ $Ox$ và $Ox'$ là hai tia đối nhau nên $Ox$ và $Ox'$ nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia $Oz$.

Suy ra, hai tia $Oy$ và $Ot$ nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia $Oz$.

Suy ra, tia $Oz$ nằm giữa hai tia $Oy$ và $Ot$. Khi đó, ta có:

$\begin{array}{l}\angle tOz + \angle zOy = \angle tOy\\\angle tOy = {100^0} + {80^0}\\\angle tOy = {180^0}\end{array}$

$\Rightarrow$ Tia $Oy$ và tia $Ot$ là hai tia đối nhau.