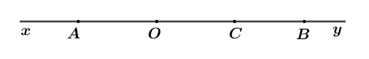Đề kiểm tra giữa kì I Toán 6 - Đề số 4 có lời giải chi tiết

Đề bài

Phần I: Trắc nghiệm (2,0 điểm)

Hãy chọn và viết vào bài làm một trong các chữ $A,\,\,B,\,\,C,\,\,D$ đứng trước phương án đúng.

Câu 1. Tập hợp $A$ các chữ số dùng để viết số $2019$ có số phần tử là:

A. $8$                                    B. $4$                                   

C. $5$                                    D. $6$

Câu 2. Cho $A = \left\{ {x|4 \le x < 9;\,\,\,x \in \mathbb{N}} \right\}$. Tổng tất cả các phần tử trong tập hợp $A$ là:

A. $30$                                  B. $26$                                 

C. $39$                                  D. $35$

Câu 3. Giá trị của số tự nhiên $x$ thỏa mãn $\left( {x + 3} \right).0 = 0$ là:

A. $x \in \mathbb{N}$                     B. $x \in \mathbb{N};\,\,x\le3$                                         

C. $x \in \mathbb{N};\,\,x \ge 3$          D. $x \in \emptyset$

Câu 4. Số $\overline {35*}$ chia hết cho $2$ và $5$ khi $\left( * \right)$ nhận giá trị là:

A. $5$                                   B. $4$                                   

C. $2$                                    D. $0$

Câu 5. Số nào sau đây chia hết cho tất cả các số $2,\,\,3,\,\,5,\,\,9$?

A. $1230$                              B. $3150$                             

C. $902$                                D. $903$

Câu 6. Tổng các ước của $8$ là:

A. $4$                                   B. $8$                                   

C. $14$                                  D. $15$

Câu 7. Cho điểm $A$ thuộc tia $OB$. Khẳng định nào sau đây đúng?

A. Tia $OA$ và tia $OB$ là hai tia đối nhau.                

B. Điểm $B$ nằm giữa hai điểm $O$ và $A$.    

C. Tia $OA$ và $OB$ là hai tia trùng nhau.                  

D. Điểm $O$ nằm giữa hai điểm $A$ và $B$.

Câu 8. Cho $4$ điểm $A,\,\,B,\,\,C,\,\,D$ trong đó không có ba điểm nào thẳng hàng. Số đoạn thẳng nhận hai trong số $4$ điểm trên làm đầu mút là:

A. $4$                                     B. $5$                                   

C. $6$                                      D. $7$

Phần II: Tự luận (8,0 điểm)

Bài 1 (2,25 điểm): Thực hiện phép tính:

a) $39.53 + 47.39$                                             

b) ${6^2}:4.3 + {2.5^2} - {1^{222}}$                        

c)$\left\{ {\left[ {{2^2}.\left( {14 - 4.3} \right) + 7} \right] + {{20192020}^0}} \right\}:{2^3}$

Bài 2 (1,5 điểm): Tìm số tự nhiên $x$, biết:

a) $96 - 3\left( {x + 1} \right) = 42$                                                                                   

b) $x \in U\left( {40} \right)$ và $x \le 20$                                                           

Bài 3 (1 điểm): Cho $A$ là tập hợp các số tự nhiên chẵn có hai chữ số sao cho tổng chữ số hàng chục và chữ số hàng đơn vị là $11$, chữ số hàng chục lớn hơn chữ số hàng đơn vị.

a) Viết tập $A$ bằng cách liệt kê phần tử.                                                                                                    

b) Viết các tập con của $A$ gồm $2$ phần tử.  

Bài 4 (3 điểm): Cho $Ox,\,\,Oy$ là hai tia đối nhau. Lấy điểm $A$ thuộc tia $Ox$, hai điểm $B$ và $C$ thuộc tia $Oy$ (điểm $C$ nằm giữa điểm $O$ và điểm $B$)

a) Hai tia $CB$ và $BC$ có phải là hai tia đối nhau không? Vì sao? Kể tên tia trùng với tia $Ox$.

b) Trong ba điểm $A,\,\,O,\,\,C$ điểm nào nằm giữa hai điểm còn lại? Vì sao?

c) Cho $OA = 2cm,\,\,AC = 4cm,\,\,OB = 5cm$. Tính độ dài $CB$.

Lời giải chi tiết

A. PHẦN TRẮC NGHIỆM

Câu 1:

Phương pháp:

Xét số chữ số của số $2019$. Từ đó viết tập hợp $A$.

Cách giải:

Ta thấy, $2019$ có $4$ chữ số là $2,\,\,0,\,\,1,\,\,9$.

$\Rightarrow A = \left\{ {2;\,\,0;\,\,1;\,\,9} \right\}$

Vậy tập hợp $A$ có $4$ phần tử.

Chọn B.

Câu 2:

Phương pháp:

Viết lại tập hợp $A$ bằng cách liệt kê phần tử.

Cách giải:

Ta có: $A = \left\{ {x|\,4 \le x < 9,\,\,x \in \mathbb{N}} \right\}$$= \left\{ {4;\,\,5;\,\,6;\,\,7;\,\,8} \right\}$

$\Rightarrow$ Tổng tất cả các phần tử trong tập hợp $A$ là: $4 + 5 + 6 + 7 + 8 = 30$

Chọn A.

Câu 3:

Phương pháp:

Áp dụng: Mọi số tự nhiên nhân với $0$ cũng bằng $0$.

Cách giải:

Theo đề bài, ta có: $\left( {x + 3} \right).0 = 0$ suy ra $x + 3$ là số tự nhiên bất kì.

Do đó, $x \in \mathbb{N}$.

Chọn A.

Câu 4:

Phương pháp:

Áp dụng dấu hiệu chia hết cho $2$ và dấu hiệu chia hết cho $5$.

Cách giải:

Để $\overline {35*}$ chia hết cho $2$ thì $* \in \left\{ {0;\,\,2;\,\,4;\,\,6;\,\,8} \right\}$.

Để $\overline {35*}$ chia hết cho $5$ thì $* \in \left\{ {0;\,\,5} \right\}$.

$\Rightarrow * = 0$

Chọn D.

Câu 5:

Phương pháp:

Áp dụng dấu hiệu chia hết cho $2,\,\,3,\,\,5,\,\,9$ và xét từng đáp án.

Cách giải:

Số chia hết cho cả $2$ và $5$ là số có chữ số hàng đơn vị là $0$ nên ta loại đáp án C và D.

+) Xét đáp án A:

Vì  nên .

$\Rightarrow$ Đáp án A sai.

+) Xét đáp án B:

Vì $3 + 1 + 5 + 0 = 9$ và $9 \vdots 3,\,\,9 \vdots 9$ nên $3150$ chia hết cho $3$ và $9$.

Vậy $3150$ chia hết cho tất cả các số $2,\,\,3,\,\,5,\,\,9$.

Chọn B.

Câu 6:

Phương pháp:

Liệt kê tất cả các ước của $8$ sau đó tính tổng.

Cách giải:

Các ước của .. là: $1;\,\,2;\,\,4;\,\,8$

Tổng tất cả các ước của $8$ là: $1 + 2 + 4 + 8 = 15$

Chọn D.

Câu 7:

Phương pháp:

Áp dụng các định nghĩa hai tia trùng nhau và hai tia đối nhau.

Cách giải:

Ta thấy, hai tia $OA$ và $OB$ có chung gốc $O$.

Mà điểm $A$ thuộc tia $OB$ nên $OA$ và $OB$ là hai tia trùng nhau.

Chọn B.

Câu 8:

Phương pháp:

Xét các đầu mút lần lượt là $A,\,\,B,\,\,C,\,\,D$.

Nếu một đầu mút là $A$ thì đầu mút còn lại là $B,\,\,C,\,\,D$. Tương tự với các điểm $B,\,\,C,\,\,D$.

Cách giải:

Các đoạn thẳng nhận hai trong $4$ điểm $A,\,\,B,\,\,C,\,\,D$ làm đầu mút là: $AB,\,\,AC,\,\,AD,\,\,BC,\,\,BD,\,\,CD$

Vậy ta được $6$ đoạn thẳng.

Chọn C.

II. TỰ LUẬN

Bài  1:

Phương pháp:

Áp dụng các công thức về lũy thừa, tính chất của phép nhân và phép cộng để thực hiện phép tính.

Cách giải:

Bài  2:

Phương pháp:

a) Sử dụng quy tắc: Chuyển vế - đổi dấu để tìm $x.$

b) Phân tích $40$ ra thừa số nguyên tố. Sau đó, tìm các cặp số là ước của $40$. Từ đó, đối chiếu với điều kiện đề bài.

Cách giải:

Tìm số tự nhiên $x$, biết:

a) $96 - 3\left( {x + 1} \right) = 42$

$\begin{array}{l}96 - 3\left( {x + 1} \right) = 42\\\,\,\,\,\,\,\,\,\,\,\,3\left( {x + 1} \right) = 96 - 42\\\,\,\,\,\,\,\,\,\,\,\,3\left( {x + 1} \right) = 54\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x + 1\,\,\,\,\, = 54:3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x + 1\,\,\,\,\,\, = 18\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\, = 18 - 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\, = 17\end{array}$

Vậy $x = 17.$

b) $x \in U\left( {40} \right)$ và $x \le 20$

Ta có: $40 = {2^3}.5$

Các ước của $40$ là: $1;\,\,2;\,\,4;\,\,5;\,\,8;\,\,10;\,\,20;\,\,40$

$\Rightarrow x \in \left\{ {1;\,\,2;\,\,4;\,\,5;\,\,8;\,\,10;\,\,20;\,\,40} \right\}$

Mà $x \le 20$ nên $x \in \left\{ {1;\,\,2;\,\,4;\,\,5;\,\,8;\,\,10;\,\,20} \right\}$

Bài  3:

Phương pháp:

Viết $11$ thành tổng của hai số có tự nhiên có một chữ số. Lập tất cả các số có hai chữ số từ tổng đó. Sau đó, đối chiếu với điều kiện đề bài, ta được tập hợp $A$ cần tìm.

Cách giải:

a) Viết tập $A$ bằng cách liệt kê phần tử.

Ta có: $11 = 2 + 9 = 3 + 8 = 4 + 7 = 5 + 6$

Các số ta lập được mà có tổng hai chữ số bằng $11$ là: $29;\,\,92;\,\,38;\,\,83;\,\,47;\,\,74;\,\,56;\,\,65.$

Vì các số cần tìm là số tự nhiên chẵn và chữ số hàng chục lớn hơn chữ số hàng đơn vị nên ta có: $92,\,\,74$ thỏa mãn.

Vậy $A = \left\{ {92;\,\,74} \right\}$.

b) Viết các tập con của $A$ gồm $2$ phần tử.

Vì tập hợp $A$ có hai phần tử nên tập con của $A$ gồm $2$ phần tử chính là tập hợp $A = \left\{ {92;\,\,74} \right\}.$

Bài 4:

Phương pháp:

a) Áp dụng định nghĩa hai tia trùng nhau, hai tia đối nhau.

b) Hai điểm $A$ và $B$ lần lượt thuộc hai tia đối nhau $Ox$ và $Oy$ thì điểm $O$ nằm giữa hai điểm $A$ và $B$.

c) Áp dụng: Nếu điểm $M$ nằm giữa hai điểm $A$ và $B$ thì $MA + MB = AB$.

Cách giải:

Theo đề bài, ta có hình vẽ:

a) Hai tia $CB$ và $BC$ có phải là hai tia đối nhau không? Vì sao? Kể tên tia trùng với tia $Ox$.

Hai tia $CB$ và $BC$ không phải là hai tia đối nhau vì hai tia $CB$và $BC$ không chung gốc.

Tia trùng với tia $Ox$ là: $OA$

b) Trong ba điểm $A,\,\,O,\,\,C$ điểm nào nằm giữa hai điểm còn lại? Vì sao?

Vì $A \in Ox$ và $C \in Oy$.

Mà $Ox$ và $Oy$ là hai tia đối nhau nên điểm $O$ nằm giữa hai điểm $A$ và $C$.

c) Cho $OA = 2cm,\,\,AC = 4cm,\,\,OB = 5cm$. Tính độ dài $CB$.

Vì điểm $O$ nằm giữa hai điểm $A$ và $C$ nên ta có:

$AO + OC = AC$$\Rightarrow OC = AC - OA$$= 4cm - 2cm = 2cm$

Theo đề bài, điểm $C$ nằm giữa hai điểm $O$ và $B$ nên ta có:

$OC + CB = OB$

$\Rightarrow CB = OB - OC$$= 5cm - 2cm = 3cm$

Vậy $CB = 3cm$.