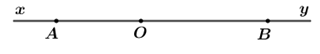Đề kiểm tra giữa kì I Toán 6 - Đề số 2 có lời giải chi tiếtĐề kiểm tra giữa kì 1 toán 6 - Đề số 2 có lời giải chi tiết Đề bài Phần I: Trắc nghiệm (2,0 điểm) Viết lại chữ cái đứng trước câu trả lời mà em cho là đúng vào bài làm. Câu 1. Tập hợp \(A = \left\{ {x \in {\mathbb{N}^*}\mid x \le 5} \right\}\) có: A. \(6\) phần tử B. \(4\) phần tử C. \(5\) phần tử D. Vô số phần tử Câu 2. Cho tập hợp \(M = \left\{ {a;\,\,b;\,\,c} \right\}\). Số tập con của \(M\) mà có hai phần tử là: A. \(7\) B. \(8\) C. \(6\) D. \(3\) Câu 3. Kết quả của phép tính \({6^6}:{6^3}\) là: A. \({1^3}\) B. \({6^3}\) C. \({{\rm{6}}^2}\) D. \(6\) Câu 4. Trong phép chia cho \(4\), số dư có thể là: A. \(0;\,\,1;\,\,2;\,\,3\) B. \(4\) C. \(1;\,\,2;\,\,3\) D. \(3\) Câu 5. Tổng \(2019 + 321\) A. chỉ chia hết cho \(9\) B. chỉ chia hết cho \(2\) và \(5\) C. chỉ chia hết cho \(2;\,\,3\) và \(5\) D. chỉ chia hết cho \(2;\,\,3;\,\,5\) và \(9\)
Câu 6. Khi viết một số tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữa số hàng đơn vị là 4, ta viết được: A. \(5\) số B. \(6\) số C. \(4\) số D. \(2019\) số Câu 7. Cho \(I\) là một điểm bất kỳ của đoạn thẳng \(MN\) thì A. điểm \(I\) hoặc trùng với điểm \(M\), hoặc trùng với điểm \(N\), hoặc nằm giữa hai điểm \(M\) và \(N\). B. điểm \(I\) phải nằm giữa hai điểm \(M\) và \(N\). C. điểm \(I\) phải trùng với điểm \(M\). D. điểm \(I\) phải trùng với điểm \(N\) Câu 8. Hai tia trùng nhau nếu A. chúng có chung gốc và cùng nằm trên một đường thẳng. B. chúng có chung gốc và có một điểm chung khác với điểm gốc. C. chúng có hai điểm chung. D. chúng có rất nhiều điểm chung Phần II: Tự luận (8,0 điểm) Câu 1: Thực hiện các phép tính sau (tính nhanh nếu có thể) a) \(20.64 + 36.20 + 19\) b) \({3^6}:{3^5} + {2.2^3} + {2020^0}\) c) \(80 - \left( {{{4.5}^2} - {{3.2}^3}} \right)\) d) \(60:\left\{ {20 - \left[ {30 - {{(5 - 1)}^2}} \right]} \right\}\) Câu 2: Tìm số tự nhiên \(x\), biết: a) \(70 - 5.\left( {x - 3} \right) = 45\) b) \(10 + 2x = {4^5}:{4^3}\) c) \({2.3^x} + {5.3^{x + 1}} = 153\) Câu 3: Vẽ hai tia đối nhau \(Ox\) và \(Oy\). Lấy điểm \(A\) thuộc tia \(Ox\), lấy điểm \(B\) thuộc tia \(Oy\). a) Viết tên các tia trùng nhau gốc \(O\). b) Trong ba điểm \(O,\,\,A,\,\,B\) điểm nào nằm giữa hai điểm còn lại? Vì sao? c) Lấy điểm \(M \notin xy\). Hãy vẽ đoạn thẳng \(MO\), tia \(MA\) và đường thẳng \(MB\)? Câu 4: a) Gọi \(A = {n^2} + n + 1\) (với \(n \in \mathbb{N}\)). Chứng tỏ rằng \(A\) không chia hết cho \(4\). b) Chứng tỏ rằng: Với mọi số tự nhiên \(n\) thì \(B = {3^{n + 3}} + {2^{n + 3}} + {3^{n + 1}} + {2^{n + 2}}\) chia hết cho \(6\). Lời giải chi tiết Phần I: Trắc nghiệm
Câu 1: Phương pháp: Viết lại tập hợp \(A\) bằng cách liệt kê phần tử. Cách giải: Vì \(x \le 5\) và \(x \in {\mathbb{N}^*}\) nên \(x \in \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\)\( \Rightarrow A = \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\) Vậy tập hợp \(A\) có \(5\) phần tử. Chọn C. Câu 2: Phương pháp: Liệt kê tất cả các tập hợp con của \(M\) gồm hai phần tử và không kể đến thứ tự của các phần tử đó trong tập hợp. Cách giải: Các tập con của \(M\) mà có hai phần tử là: \(\left\{ {a;\,\,b} \right\},\,\,\left\{ {a;\,\,c} \right\},\,\,\left\{ {b;\,\,c} \right\}\) Vậy có \(3\) tập con của \(M\) gồm có \(2\) phần tử. Chọn D. Câu 3: Phương pháp: Áp dụng quy tắc chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\,\,\,\left( {m \ge n,\,\,a \in {\mathbb{N}^*},\,\,a \ne 1} \right).\) Cách giải: Ta có: \({6^6}:{6^3} = {6^{6 - 3}} = {6^3}\) Chọn B. Câu 4: Phương pháp: Áp dụng kiến thức: Trong phép chia, số dư luôn luôn nhỏ hơn số chia. Cách giải: Trong phép chia cho \(4\), số dư có thể là: \(0;\,\,1;\,\,2;\,\,3\) Chọn A. Câu 5: Phương pháp: Áp dụng các dấu hiệu chia hết cho \(2;\,\,3;\,\,5;\,\,9\) Cách giải: Ta có: \(2019 + 321 = 2340\) Vì \(2340\) có chữ số tận cùng là \(0\) nên \(2340\) chia hết cho \(2\) và \(5\). Vì \(2 + 3 + 4 + 0 = 9\) nên \(2340\)chia hết cho \(3\) và \(9\). Vậy \(2340\) chia hết cho cả \(2,\,\,3,\,\,5,\,\,9\). Chọn D. Câu 6: Phương pháp: Viết tất cả các số tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữ số hàng đơn vị là \(6\). Cách giải: Các số tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữ số hàng đơn vị là \(4\) là: \(40;\,\,51;\,\,62;\,\,73;\,\,84;\,\,95\) Vậy ta viết được \(6\) số thỏa mãn bài toán. Chọn B. Câu 7: Phương pháp: Áp dụng định nghĩa đoạn thẳng. Cách giải: Nếu \(I\) là một điểm bất kỳ của đoạn thẳng \(MN\) thì điểm \(I\) hoặc trùng với điểm \(M\), hoặc trùng với điểm \(N\), hoặc nằm giữa hai điểm \(M\) và \(N\). Chọn A. Câu 8: Phương pháp: Áp dụng định nghĩa hai tia trùng nhau. Cách giải: Áp dụng định nghĩa hai tia trùng nhau ta có: Hai tia trùng nhau nếu chúng có chung gốc và có một điểm chung khác điểm gốc. Chọn B. II. TỰ LUẬN Câu 1: Phương pháp: a) Áp dụng các tính chất phân phối của phép nhân và phép cộng để tính nhanh. b) Áp dụng quy tắc nhân, chia hai lũy thừa cùng cơ số, thứ tự thực hiện phép tính. c), d) Áp dụng các phép toán về lũy thừa, thứ tự thực hiện phép tính. Cách giải: Thực hiện các phép tính (tính nhanh nếu có thể)
Câu 2: Phương pháp: +) Sử dụng các quy tắc chuyển vế - đổi dấu. +) Sử dụng các công thức lũy thừa: \({a^m}.{a^n} = {a^{m + n}}\) và \({a^m}:{a^n} = {a^{m - n}}\) với \(a \in {\mathbb{N}^*},\,\,a \ne 1,\,\,m \ge n.\) Cách giải:
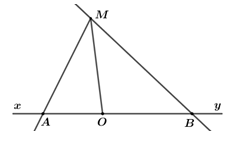
c) \({2.3^x} + {5.3^{x + 1}} = 153\) \(\begin{array}{l}{2.3^x} + {5.3.3^x} = 153\\{2.3^x} + {15.3^x} = 153\\\,\,\,\,\,\,\,\,{17.3^x}\,\,\,\,\,\,\,\,\, = 153\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{3^x}\,\,\,\,\,\,\,\,\, = 153:17\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{3^x}\,\,\,\,\,\,\,\,\, = 9\\ \Rightarrow x = 2\end{array}\) Vậy \(x = 2\). Câu 3: Phương pháp: a) Áp dụng định nghĩa hai tia trùng nhau: Hai tia trùng nhau nếu chúng có chung gốc và có một điểm chung khác gốc. b) Nếu hai thuộc hai đối nhau thì điểm gốc sẽ nằm giữa hai điểm đó. c) Áp dụng định nghĩa đoạn thẳng, tia, đường thẳng. Cách giải: Vẽ hai tia đối nhau \(Ox\) và \(Oy\). Lấy điểm \(A\) thuộc tia \(Ox\), lấy điểm \(B\) thuộc tia \(Oy\). a) Viết tên các tia trùng nhau gốc \(O\). Các tia trùng nhau gốc \(O\) là: \(OA\) với \(Ox\) và \(OB\) với \(Oy.\) b) Trong ba điểm \(O,\,\,A,\,\,B\) điểm nào nằm giữa hai điểm còn lại? Vì sao? Vì \(A \in Ox,\,\,B \in Oy\) mà \(Ox\) và \(Oy\) là hai tia đối nhau nên \(O\) nằm giữa \(A\) và \(B\). c) Lấy điểm \(M \notin xy\). Hãy vẽ đoạn thẳng \(MO\), tia \(MA\) và đường thẳng \(MB\)? Lấy một điểm \(M\) bất kì không thuộc đường thẳng \(xy.\) Nối \(M\) với \(O\) ta được đoạn thẳng \(MO.\) Từ điểm \(M,\) nối \(M,\,\,A\) và kéo dài về phía điểm \(A\) ta được tia \(MA.\) Vẽ đường thẳng đi qua hai điểm \(M,\,\,B\) ta được đường thẳng \(MB.\) Câu 4: Phương pháp: a) Chứng minh \(A\) không chia hết cho \(4\) thì \(A\) không chia hết cho \(2\). b) Áp dụng tính chất chia hết của một tổng. Cách giải: a) Gọi \(A = {n^2} + n + 1\) (với \(n \in \mathbb{N}\)). Chứng tỏ rằng \(A\) không chia hết cho \(4\). Ta có: \(A = {n^2} + n + 1 = n\left( {n + 1} \right) + 1\) Vì \(n \in \mathbb{N}\) nên \(n + 1 \in \mathbb{N}\). Do đó, \(n\) và \(n + 1\) là hai số tự nhiên liên tiếp. Vì tích hai số tự nhiên liên tiếp chia hết cho \(2\) nên \(n\left( {n + 1} \right)\) chia hết cho \(2\). Mà \(1\) không chia hết cho \(2\) nên \(n\left( {n + 1} \right) + 1\) không chia hết cho \(2\). \( \Rightarrow \) \(A\) không chia hết cho \(4\). b) Chứng tỏ rằng: Với mọi số tự nhiên \(n\) thì chia hết cho \(6\). Ta có: \(\begin{array}{l}B = {3^{n + 3}} + {2^{n + 3}} + {3^{n + 1}} + {2^{n + 2}}\\\,\,\,\,\, = \left( {{3^{n + 3}} + {3^{n + 1}}} \right) + \left( {{2^{n + 3}} + {2^{n + 2}}} \right)\\\,\,\,\,\, = {3^{n + 1}}\left( {{3^2} + 1} \right) + {2^{n + 2}}\left( {2 + 1} \right)\\\,\,\,\,\, = {3^{n + 1}}.10 + {2^{n + 2}}.3\\\,\,\,\,\, = {5.6.3^n} + {6.2^{n + 1}}\\\,\,\,\,\, = 6\left( {{{5.3}^n} + {2^{n + 1}}} \right)\,\,\, \vdots \,\,6\end{array}\) \( \Rightarrow B\) chia hết cho \(6\) với mọi số tự nhiên \(n\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
