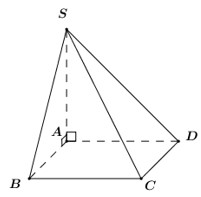
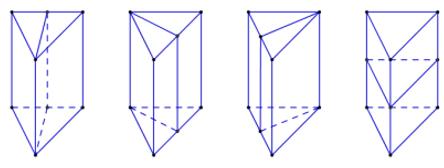
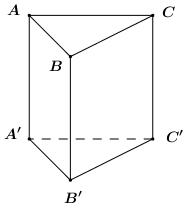
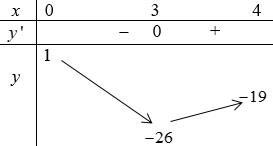
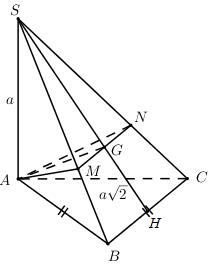
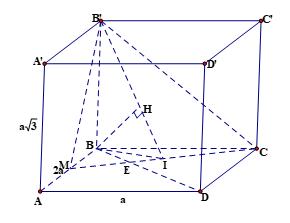
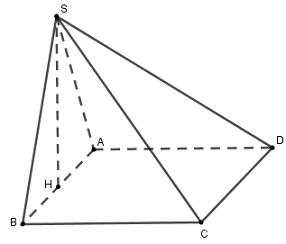
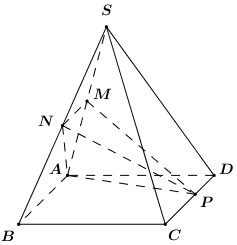
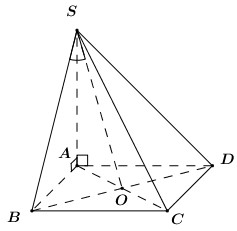
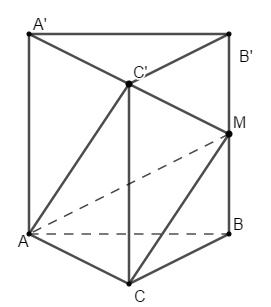
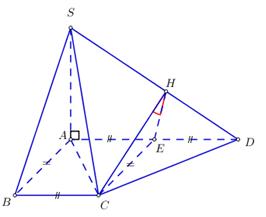
Đề kiểm tra giữa kì 2 Toán 12 - đề số 5 có lời giải chi tiếtĐáp án và lời giải chi tiết Đề kiểm tra giữa kì 2 Toán 12 Đề bài Câu 1: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 3 B. 1 C. 2 D. 4 Câu 2: Cho hàm số \(y = \dfrac{{{x^2} + x}}{{x - 2}}\) có đồ thị \(\left( C \right)\). Phương trình tiếp tuyến tại điểm \(A\left( {1; - 2} \right)\) của \(\left( C \right)\) là A. \(y = - 3x + 5.\) B. \(y = - 5x + 7\) C. \(y = - 5x + 3\) D. \(y = - 4x + 6\) Câu 3: Gọi \(\left( P \right)\) là đồ thị hàm số \(y = 2{x^3} - x + 3\). Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của \(\left( P \right)\)? A. \(y = - x - 3\) B. \(y = 11x + 4\) C. \(y = - x + 3\) D. \(y = 4x - 1\) Câu 4: Khối đa diện đều loại \(\left\{ {4;3} \right\}\) có bao nhiêu mặt? A. 6. B. 20 C. 12 D. 8 Câu 5: Cho lăng trụ \(ABC.A'B'C'\) có các mặt bên là hình vuông cạnh \(a\sqrt 2 \). Tính theo a thể tích V của khối lăng trụ ABC,A’B’C’. A. \(V = \dfrac{{\sqrt 6 {a^3}}}{2}\) B. \(V = \dfrac{{\sqrt 3 {a^3}}}{{12}}\) C. \(V = \dfrac{{\sqrt 3 {a^3}}}{4}\) D. \(V = \dfrac{{\sqrt 6 {a^3}}}{6}\) Câu 6: Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh a, \(SA = \sqrt 2 a\) và SA vuông góc với \(\left( {ABCD} \right)\). Góc giữa SC và ABCD bằng A. \({45^0}\) B. \({30^0}\) C. \({60^0}\) D. \({90^0}\) Câu 7: Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Tính khoảng cách giữa hai đường thẳng \(AB'\) và \(CD'\). A. \(\dfrac{{\sqrt 2 a}}{2}\) B. a C. \(\sqrt 2 a\) D. 2a Câu 8: Giá trị cực đại của hàm số \(y = {x^3} - 12x + 20\) là: A. \({y_{CD}} = 4\) B. \({y_{CD}} = 36\) C. \({y_{CD}} = - 4\) D. \({y_{CD}} = - 2\) Câu 9: Tập xác định của hàm số \(y = \dfrac{1}{{\sqrt {\sin x + 1} }}\) là A. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\) B. \(\mathbb{R}\backslash \left\{ { - \dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\) C. \(\mathbb{R}\backslash \left\{ { - \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) D. \(\mathbb{R}\) Câu 10: Nghiệm âm lớn nhất của phương trình \(\dfrac{{\sqrt 3 }}{{{{\sin }^2}x}} = 3\cot x + \sqrt 3 \) là A. \( - \dfrac{\pi }{6}.\) B. \( - \dfrac{{5\pi }}{6}.\) C. \( - \dfrac{\pi }{2}.\) D. \( - \dfrac{{2\pi }}{3}.\) Câu 11: Cho cấp số cộng \(\left( {{u_n}} \right)\) có các số hạng đầu lần lượt là 5; 9; 13; 17... Tìm công thức số hạng tổng quát \({u_n}\) của cấp số cộng? A. \({u_n} = 5n - 1.\) B. \({u_n} = 5n + 1.\) C. \({u_n} = 4n - 1\) D. \({u_n} = 4n + 1\) Câu 12: Tìm giá trị nhỏ nhất của hàm số \(y = {x^2} - 1\) trên đoạn \(\left[ { - 3;2} \right]?\) A. \(\mathop {\min }\limits_{\left[ { - 3;2} \right]} y = 3\) B. \(\mathop {\min }\limits_{\left[ { - 3;2} \right]} y = - 3\) C. \(\mathop {\min }\limits_{\left[ { - 3;2} \right]} y = - 1\) D. \(\mathop {\min }\limits_{\left[ { - 3;2} \right]} y = 8\) Câu 13: Cho hàm số \(y = \sqrt {{x^2} - 1} \). Mệnh đề nào dưới đây đúng? A. Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) C. Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\) D. Hàm số đồng biến trên khoảng \(\left( {{u_n}} \right)\) Câu 14: Khai triển \({\left( {x - 3} \right)^{100}}\) ta được đa thức \({\left( {x - 3} \right)^{100}} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_{100}}{x^{100}}\), \({a_1},\,\,{a_2},...,{a_{100}}\) là các hệ số thực. Tính \({a_0} - {a_1} + {a_2} - ... - {a_{99}} + {a_{100}}?\) A. \( - {2^{100}}\) B. \({4^{100}}\) C. \( - {4^{100}}\) D. \({2^{100}}\) Câu 15: Nghiệm của phương trình lượng giác \({\cos ^2}x - \cos x = 0\) thỏa mãn điều kiện \(0 < x < \pi \) là: A. \(x = 0\) B. \(x = \dfrac{{3\pi }}{4}\) C. \(x = \dfrac{\pi }{2}\) D. \(x = - \dfrac{\pi }{2}\) Câu 16: Tất cả các nghiệm của phương trình \(\tan x = \cot x\) là: A. \(x = \dfrac{\pi }{4} + k\dfrac{\pi }{4},k \in \mathbb{Z}\) B. \(x = \dfrac{\pi }{4} + k2\pi ,k \in \mathbb{Z}\) C. \(x = \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\) D. \(x = \dfrac{\pi }{4} + k\dfrac{\pi }{2},k \in \mathbb{Z}\) Câu 17: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\) , cạnh bên \(SA = a\sqrt 2 \) và vuông góc với \(\left( {ABCD} \right)\). Tính theo \(a\) thể tích \(V\) của khối chóp \(S.ABC\)? A. \(V = \dfrac{{\sqrt 2 }}{6}{a^3}\) B. \(V = \dfrac{{2\sqrt 2 }}{3}{a^3}\) C. \(V = \sqrt 2 {a^3}\) D. \(V = \dfrac{{\sqrt 2 }}{3}{a^3}\) Câu 18: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(AB = a,\,\,SA = a\sqrt 3 \) và vuông góc với \(\left( {ABCD} \right)\). Tính góc giữa hai đường thẳng SB và CD. A. \({60^0}\) B. \({30^0}\) C. \({45^0}\) D. \({90^0}\) Câu 19: Cho hàm số \(y = \dfrac{{3x - 1}}{{x - 3}}\) có đồ thị \(\left( C \right)\). Mệnh đề nào sau đây sai? A. Đồ thị \(\left( C \right)\) có tiệm cận ngang và tiệm cận đứng. B. Đồ thị \(\left( C \right)\) không có tiệm cận đứng. C. Đồ thị \(\left( C \right)\) có tiệm cận ngang. D. Đồ thị \(\left( C \right)\) có tiệm cận. Câu 20: Trong năm học 2018-2019 trường THPT chuyên đại học Vinh có 13 học sinh khối 10, 12 học sinh khối 11, 12 học sinh khối 12. Nhân ngày nhà giáo Việt Nam 20 tháng 11 nhà trường chọn ngẫu nhiên 2 lớp trong trường để tham gia hội văn nghệ của trường Đại học Vinh. Xác suất để chọn được hai lớp không cùng khối là: A. \(\dfrac{{76}}{{111}}\) B. \(\dfrac{{87}}{{111}}\) C. \(\dfrac{{78}}{{111}}\) D. \(\dfrac{{67}}{{111}}\) Câu 21: Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\),\(BC = 2a,\) \(SA = a\) và \(SA\) vuông góc với đáy. Tính góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\)? A. \({45^0}\) B. \({30^0}\) C. \({60^0}\) D. \({90^0}\) Câu 22: Gọi \({x_1},\,\,{x_2},\,\,{x_3}\) là các cực trị của hàm số \(y = - {x^4} + 4{x^2} + 2019\). Tính tổng \({x_1} + {x_2} + {x_3}\) A. 0 B. \(2\sqrt 2 \) C. \( - 1\) D. 2 Câu 23: Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 1\) trên đoạn \(\left[ {0;4} \right]\). Tính tổng \(m + 2M\). A. \(m + 2M = 17\) B. \(m + 2M = - 37\) C. \(m + 2M = 51\) D. \(m + 2M = - 24\) Câu 24: Cho cấp số nhân \(\left( {{u_n}} \right)\) thỏa mãn \(\left\{ \begin{array}{l}{u_1} - {u_3} + {u_5} = 65\\{u_1} + {u_7} = 325\end{array} \right.\). Tính \({u_3}\)? A. \({u_3} = 15\) B. \({u_3} = 25\) C. \({u_3} = 10\) D. \({u_3} = 20\) Câu 25: Biết số tự nhiên \(n\) thỏa mãn \(C_n^1 + 2\dfrac{{C_n^2}}{{C_n^1}} + ... + n\dfrac{{C_n^n}}{{C_n^{n - 1}}} = 45\). Tính \(C_{n + 4}^n?\) A. 715. B. 1820 C. 1365 D. 1001 Câu 26: Tìm tất cả các giá trị của \(m\) để hàm số \(y = \dfrac{{x - 1}}{{x + m}}\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\)? A. \(\left( { - 1; + \infty } \right)\) B. \(\left[ {0; + \infty } \right)\) C. \(\left( {0; + \infty } \right)\) D. \(\left[ { - 1; + \infty } \right)\) Câu 27: Tìm tất cả các giá trị thực của tham số \(m\) sao cho điểm cực tiểu của đồ thị hàm số \(y = {x^3} + {x^2} + mx - 1\) nằm bên phải trục tung? A. \(m < 0\) B. \(0 < m < \dfrac{1}{3}\) C. \(m < \dfrac{1}{3}\) D. Không tồn tại Câu 28: Trên một cái bảng đã ghi sẵn các số tự nhiên từ 1 đến 2020. Ta thực hiện công việc như sau: xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng là: A. 4040 B. 2041210 C. 4082420 D. 2020 Câu 29: Số nghiệm của phương trình \(\sin 5x + \sqrt 3 \cos 5x = 2\sin 7x\) trên khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\)là? A. 4. B. 1. C. 3. D. 2. Câu 30: Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và \(f'\left( x \right) > 0,\,\,\forall x \in \mathbb{R}\). Biết \(f\left( 1 \right) = 2\). Hỏi khẳng định nào sau đây có thể xảy ra? A. \(f\left( 2 \right) + f\left( 3 \right) = 4\) B. \(f\left( { - 1} \right) = 2\) C. \(f\left( 2 \right) = 1\) D. \(f\left( {2018} \right) < f\left( {2019} \right)\) Câu 31: Cho tập hợp \(A = \left\{ {0;1;2;3;4;5;6} \right\}\). Từ A lập được bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau và nhỏ hơn 4012. A. 180 B. 240 C. 200 D. 220 Câu 32: Một vật chuyển động theo quy luật \(s = - \dfrac{1}{2}{t^3} + 9{t^2}\) với t (giây) là khoảng thời gian tứ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. \(216\left( {m/s} \right)\) B. 400\(\left( {m/s} \right)\) C. 54\(\left( {m/s} \right)\) D. 30\(\left( {m/s} \right)\) Câu 33: Tất cả các giá trị của tham số \(m\) để hàm số \(y = \left( {m - 1} \right){x^4}\) đạt cực đại tại \(x = 0\) là: A. \(m < 1\) B. \(m > 1\) C. không tồn tại m D. \(m = 1\) Câu 34: Tung hai con súc sắc 3 lần độc lập với nhau. Tính xác suất để có đúng một lần tổng số chấm xuất hiện ở hai con súc sắc bằng 6. (Kết quả làm tròn đến 3 chữ số phần thập phân) A. 0,120 B. 0,319 C. 0,718 D. 0,309 Câu 35: Hệ số của \({x^5}\) trong khai triển \({\left( {1 - 2x - 3{x^2}} \right)^9}\) là: A. 792 B. \( - 684\) C. 3528 D. 0 Câu 36: Cho một khối đa diện lỗi có 10 đỉnh, 7 mặt. Hỏi khối đa diện có mấy cạnh? A. 20 B. 18 C. 15 D. 12 Câu 37: Cho hình chóp S.ABC có đáy là \(\Delta ABC\) vuông cân ở \(B,{\mkern 1mu} \)\(AC = a\sqrt 2 ,{\mkern 1mu} \)\(SA \bot \left( {ABC} \right),\) \(SA = a.\) Gọi \(G\) là trọng tâm của \(\Delta SBC\), \(mp\left( {\alpha {\rm{\;}}} \right)\) đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi \(V\)là thể tích của khối đa diện không chứa đỉnh \(S\). Tính V. A. \(\dfrac{{5{a^3}}}{{54}}.\) B. \(\dfrac{{4{a^3}}}{9}.\) C. \(\dfrac{{2{a^3}}}{9}.\) D. \(\dfrac{{4{a^3}}}{{27}}.\) Câu 38: Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 2a\), \(AD = a\), \(AA' = a\sqrt 3 \). Gọi \(M\) là trung điểm cạnh \(AB\). Tính khoảng cách \(h\) từ điểm \(D\) đến mặt phẳng \(\left( {B'MC} \right).\) A. \(h = \dfrac{{3a\sqrt {21} }}{7}\) B. \(h = \dfrac{a}{{\sqrt {21} }}\) C. \(h = \dfrac{{a\sqrt {21} }}{{14}}\) D. \(h = \dfrac{{2a\sqrt {21} }}{7}\) Câu 39: Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), mặt bên \(SAB\) nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right),\) \(\widehat {SAB} = {30^0},SA = 2a.\) Tính thể tích \(V\) của khối chóp \(S.ABCD\). A. \(V = \dfrac{{\sqrt 3 {a^3}}}{6}.\) B. \(V = {a^3}.\) C. \(V = \dfrac{{{a^3}}}{9}.\) D. \(V = \dfrac{{{a^3}}}{3}.\) Câu 40: Số tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{\left| x \right| - 2018}}{{x + 2019}}\) là: A. 1 B. 3 C. 2 D. 0 Câu 41: Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\). Gọi \(M,\,\,N\) lần lượt là trung điểm các cạnh \(SA,\,\,SB\) và \(P\) là điểm bất kỳ thuộc cạnh \(CD\). Biết thể tích khối chóp \(S.ABCD\) là \(V\). Tính thể tích của khối tứ diện \(AMNP\) theo \(V\). A. \(\dfrac{V}{8}\) B. \(\dfrac{V}{{12}}\) C. \(\dfrac{V}{6}\) D. \(\dfrac{V}{4}\) Câu 42: Đồ thị hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng \(x = 1\) tại điểm có tung độ bằng 3 khi A. \(a = b = 0,\,\,c = 2\) B. \(a = c = 0,\,\,b = 2\) C. \(a = 2,\,\,b = c = 0\) D. \(a = 2,\,\,b = 1,\,\,c = 0\) Câu 43: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(2a\), cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = 2a\). Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SAC} \right)\) bằng: A. \({90^0}\) B. \({45^0}\) C. \({60^0}\) D. \({30^0}\) Câu 44: Trong mặt phẳng Oxy, có bao nhiêu điểm mà từ đó kẻ được hai tiếp tuyến đến đồ thị hàm số \(y = \dfrac{{{x^3}}}{3} - \dfrac{{{x^2}}}{2} + x + 1\) sao cho hai tiếp tuyến này vuông góc với nhau? A. 0 B. 1 C. 2 D. Vô số Câu 45: Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác cân tại C ,\(\angle BAC = 30^\circ ,\) \(AB = a\sqrt 3 ,\) \(AA' = a\). Gọi \(M\) là trung điểm của \(BB'\). Tính theo \(a\) thể tích \(V\) của khối tứ diện \(MACC'\). A. \(V = \dfrac{{{a^3}\sqrt 3 }}{{12}}\) B. \(V = \dfrac{{{a^3}\sqrt 3 }}{4}\) C. \(V = \dfrac{{{a^3}\sqrt 3 }}{3}\) D. \(V = \dfrac{{{a^3}\sqrt 3 }}{{18}}\) Câu 46: Cho hàm số \(f\left( x \right)\) có \(f\left( 2 \right) = f\left( { - 2} \right) = 0\) và có bảng xét dấu của đạo hàm như sau: Hàm số \(y = {\left( {f\left( {3 - x} \right)} \right)^2}\) nghịch biến trên khoảng nào dưới đây? A. \(\left( {2;5} \right)\) B. \(\left( {1; + \infty } \right)\) C. \(\left( { - 2; - 1} \right)\) D. \(\left( {1;2} \right)\) Câu 47: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: Khi đó số nghiệm của phương trình \(2\left| {f\left( {2x - 3} \right)} \right| - 5 = 0\) là: A. 3 B. 2 C. 4 D. 1 Câu 48: Tìm số tiệm cận (bao gồm cả tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số \(y = \dfrac{{\sqrt {4{x^2} + 5} }}{{\sqrt {2x + 1} - x - 1}}\). A. 3 B. 1 C. 2 D. 4 Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, biết \(AB = BC = a\), \(AD = 2a\) và SA vuông góc với mặt phẳng đáy, \(SA = a\sqrt 2 \) Xác định số đo của góc \(\varphi \) là góc giữa hai mặt phẳng (SCD) và (SAD). A. \(\varphi = {60^0}\) B. \(\varphi = {45^0}\) C. \(\varphi = {30^0}\) D. \(\varphi = {90^0}\) Câu 50: Tìm tất cả các giá trị thực của tham số \(m\) sao cho hàm số \(y = \dfrac{{m{x^3}}}{3} + 7m{x^2} + 14x - m + 2\) nghịch biến trên \(\left[ {1; + \infty } \right)\). A. \(\left( { - \infty ; - \dfrac{{14}}{{15}}} \right)\) B. \(\left( { - \infty ; - \dfrac{{14}}{{15}}} \right]\) C. \(\left[ { - 2; - \dfrac{{14}}{{15}}} \right]\) D. \(\left[ { - \dfrac{{14}}{{15}}; + \infty } \right)\) Lời giải chi tiết Câu 1: Phương pháp: Vẽ hình và đếm. Cách giải: Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng.
Chọn D. Câu 2: Phương pháp: Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(A\left( {{x_0};{y_0}} \right)\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\) Cách giải: TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\). Ta có \(y = \dfrac{{{x^2} + x}}{{x - 2}}\)\( \Rightarrow y' = \dfrac{{\left( {2x + 1} \right)\left( {x - 2} \right) - \left( {{x^2} + x} \right)}}{{{{\left( {x - 2} \right)}^2}}}\)\( = \dfrac{{{x^2} - 4x - 2}}{{{{\left( {x - 2} \right)}^2}}}\) Tiếp tuyến tại \(A\left( {1; - 2} \right)\) có hệ số góc là \(k = y'\left( 1 \right) = - 5\). Vậy tiếp tuyến tại \(A\left( {1; - 2} \right)\) của đồ thị hàm số là: \(y = - 5\left( {x - 1} \right) - 2 \Leftrightarrow y = - 5x + 3\). Chọn C. Câu 3: Phương pháp: Hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) tiếp xúc với nhau khi và chỉ khi hệ phương trình \(\left\{ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f'\left( x \right) = g'\left( x \right)\end{array} \right.\) có nghiệm. Cách giải: Xét đáp án C: \(y = g\left( x \right) = - x + 3 \Leftrightarrow g'\left( x \right) = - 1\). Ta có: \(y = f\left( x \right) = 2{x^3} - x + 3\)\( \Rightarrow f'\left( x \right) = 6x - 1\). Xét hệ phương trình \(\left\{ \begin{array}{l}2{x^3} - x + 3 = - x + 3\\6x - 1 = - 1\end{array} \right. \Leftrightarrow x = 0\). Vậy đường thẳng \(y = - x + 3\) tiếp xúc với đồ thị hàm số \(y = 2{x^3} - x + 3\) tại điểm có hoành độ bằng 0. Chọn C. Câu 4: Phương pháp: Vẽ hình và đếm số mặt. Cách giải: Khối đa diện đều loại \(\left\{ {4;3} \right\}\) là hình lập phương và có 6 mặt. Chọn A. Câu 5: Phương pháp: - Tìm chiều cao hình lăng trụ. - Áp dụng công thức tính thể tích có chiều cao \(h\), diện tích đáy \(B\) là \(V = Bh\). Cách giải: Vì các mặt bên của lăng trụ là hình vuông nên ta có \(\left\{ \begin{array}{l}AA' \bot AB\\AA' \bot AC\end{array} \right. \Rightarrow AA' \bot \left( {ABCD} \right)\) và \(AA' = a\sqrt 2 \). Đồng thời \(AB = BC = CA = a\sqrt 2 \Rightarrow \Delta ABC\) là tam giác đều cạnh \(a\sqrt 2 \) \( \Rightarrow {S_{\Delta ABC}} = {\left( {a\sqrt 2 } \right)^2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\). Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}}\)\( = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 6 }}{2}\). Chọn A. Câu 6: Phương pháp: - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu vuông góc của nó trên mặt phẳng đó. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Cách giải: Ta có \(SA \bot \left( {ABCD} \right)\) \( \Rightarrow AC\) là hình chiếu vuông góc của \(SC\) lên \(\left( {ABCD} \right)\). \( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;AC} \right) = \angle SCA\). Vì \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = a\sqrt 2 = SA \Rightarrow \Delta SAC\) vuông cân tại \(A\) \( \Rightarrow \angle SCA = {45^0}\). Vậy \(\angle \left( {SC;\left( {ABCD} \right)} \right) = {45^0}\). Chọn A. Câu 7: Phương pháp: - Tìm đoạn vuông góc chung của hai đường thẳng. - Khoảng cách giữa hai đường thẳng chéo nhau bằng độ dài đoạn vuông góc chung của chúng. Cách giải: Ta có \(\left\{ \begin{array}{l}AD \bot \left( {ABB'A'} \right) \Rightarrow AD \bot AB'\\AD \bot \left( {CDD'C'} \right) \Rightarrow AD \bot CD'\end{array} \right.\)\( \Rightarrow d\left( {AB';CD'} \right) = AD = a\). Chọn B. Câu 8: Phương pháp: - Hàm số \(y = f\left( x \right)\) đạt cực đại đại điểm \(x = {x_0}\) khi và chỉ khi \(\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.\) (hàm đa thức bậc ba). - Thay điểm cực đại của hàm số vào hàm số để tìm giá trị cực đại. Cách giải: Ta có: \(\left\{ \begin{array}{l}y' = 3{x^2} - 12x\\y'' = 6x - 12\end{array} \right.\). Xét hệ \( \Leftrightarrow \left\{ \begin{array}{l}x = \pm 2\\x < 2\end{array} \right. \Rightarrow x = - 2\) là điểm cực đại của hàm số. Ta có: \({y_{CD}} = y\left( { - 2} \right) = {\left( { - 2} \right)^3} - 12.\left( { - 2} \right) + 20 = 36\). Chọn B. Câu 9: Phương pháp: - Hàm số \(y = \dfrac{1}{{\sqrt A }}\) xác định khi và chỉ khi \(A > 0\). - Sử dụng tính chất: \( - 1 \le \sin x \le 1\,\,\forall x \in \mathbb{R}\). Cách giải: Hàm số \(y = \dfrac{1}{{\sqrt {\sin x + 1} }}\) xác định khi và chỉ khi \(\sin x + 1 > 0 \Leftrightarrow \sin x > - 1\). Ta có: \(\sin x \ge - 1\,\,\forall x \in \mathbb{R}\). Do đó \(\sin x > - 1 \Leftrightarrow \sin x \ne - 1\)\( \Leftrightarrow x \ne - \dfrac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\). Vậy TXĐ của hàm số là \(D = \mathbb{R}\backslash \left\{ { - \dfrac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\). Chọn B. Câu 10: Phương pháp: - Tìm ĐKXĐ của phương trình. - Sử dụng công thức \(\dfrac{1}{{{{\sin }^2}x}} = 1 + {\cot ^2}x\). - Giải phương trình bậc hai đối với một hàm số lượng giác. - Giải bất phương trình \(x < 0\), tìm số nguyên \(k\) lớn nhất thỏa mãn, từ đó tìm nghiệm âm lớn nhất của phương trình. Cách giải: ĐKXĐ: \(\sin x \ne 0 \Leftrightarrow x \ne k\pi \). Ta có: \(\begin{array}{l}\,\,\,\,\,\,\dfrac{{\sqrt 3 }}{{{{\sin }^2}x}} = 3\cot x + \sqrt 3 \\ \Leftrightarrow \sqrt 3 \left( {1 + {{\cot }^2}x} \right) = 3\cot x + \sqrt 3 \\ \Leftrightarrow \sqrt 3 {\cot ^2}x - 3\cot x = 0\\ \Leftrightarrow \sqrt 3 \cot x\left( {\cot x - \sqrt 3 } \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cot x = 0\\\cot x = \sqrt 3 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = \dfrac{\pi }{6} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\) + Xét họ nghiệm \(x = \dfrac{\pi }{2} + k\pi \). Cho \(x < 0 \Leftrightarrow \dfrac{\pi }{2} + k\pi < 0 \Leftrightarrow k < - \dfrac{1}{2}\). Mà \(k \in \mathbb{Z} \Rightarrow {k_{\max }} = - 1\) \( \Rightarrow \) Nghiệm âm lớn nhất là \(x = \dfrac{\pi }{2} - \pi = - \dfrac{\pi }{2}\). + Xét họ nghiệm \(x = \dfrac{\pi }{6} + k\pi \). Cho \(x < 0 \Leftrightarrow \dfrac{\pi }{6} + k\pi < 0 \Leftrightarrow k < - \dfrac{1}{6}\). Mà \(k \in \mathbb{Z} \Rightarrow {k_{\max }} = - 1\) \( \Rightarrow \) Nghiệm âm lớn nhất là \(x = \dfrac{\pi }{6} - \pi = - \dfrac{{5\pi }}{6}\). Ta có: \( - \dfrac{\pi }{2} > - \dfrac{{5\pi }}{6}\). Vậy nghiệm âm lớn nhất của phương trình là \(x = - \dfrac{\pi }{2}\). Chọn C. Câu 11: Phương pháp: - Xác định số hạng đầu \({u_1}\) và công sai \(d = {u_2} - {u_1}\) của cấp số cộng. - Cấp số cộng có số hạng đầu \({u_1}\) và công sai \(d\) có SHTQ: \({u_n} = {u_1} + \left( {n - 1} \right)d\). Cách giải: Dãy số \(5;9;13;17...\) có số hạng đầu \({u_1} = 5\) và công sai \(d = {u_2} - {u_1} = 9 - 5 = 4\). Vậy SHTQ của cấp số cộng trên là \({u_n} = {u_1} + \left( {n - 1} \right)d = 5 + \left( {n - 1} \right).4 = 4n + 1\). Chọn D. Câu 12: Phương pháp: - Tính đạo hàm của hàm số, giải phương trình \(y' = 0\) xác định các nghiệm \({x_i} \in \left[ { - 3;2} \right]\). - Tính các giá trị: \(y\left( {{x_i}} \right);\,\,y\left( { - 3} \right);\,\,y\left( 2 \right)\). - Kết luận: \(\mathop {max}\limits_{\left[ { - 3;2} \right]} y = \max \left\{ {y\left( {{x_i}} \right);\,\,y\left( { - 3} \right);\,\,y\left( 2 \right)} \right\}\), \(\mathop {min}\limits_{\left[ { - 3;2} \right]} y = \min \left\{ {y\left( {{x_i}} \right);\,\,y\left( { - 3} \right);\,\,y\left( 2 \right)} \right\}\). Cách giải: TXĐ: \(D = \mathbb{R}\). Ta có \(y = {x^2} - 1 \Rightarrow y' = 2x = 0\)\( \Leftrightarrow x = 0 \in \left[ { - 3;2} \right]\). \(y\left( { - 3} \right) = 8,\,\,y\left( 0 \right) = - 1,\,\,y\left( 2 \right) = 3\). Vậy \(\mathop {min}\limits_{\left[ { - 3;2} \right]} y = y\left( 0 \right) = - 1\). Chọn C. Câu 13(: Phương pháp: - Tìm TXĐ của hàm số. - Tính đạo hàm, lập BXD và kết luận các khoảng đồng biến, nghịch biến của hàm số. Cách giải: TXĐ: \(D = \left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\). Ta có \(y' = \dfrac{x}{{\sqrt {{x^2} - 1} }} = 0 \Leftrightarrow x = 0\,\,\,\left( {KTM} \right)\). Bảng xét dấu: Từ BXD ta thấy hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\) là mệnh đề đúng. Chọn C. Câu 14: Phương pháp: Tìm \(f\left( { - 1} \right)\) để tìm đáp án. Cách giải: Ta thấy \({\left( {x - 3} \right)^{100}} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_{100}}{x^{100}}\) \( \Rightarrow {\left( { - 1 - 3} \right)^{100}} = {a_0} - {a_1} + {a_2} - {a_3} + .... + {a_{100}}\) \( \Rightarrow {a_0} - {a_1} + {a_2} - {a_3} + .... + {a_{100}} = {4^{100}}\). Chọn B. Câu 15: Phương pháp: - Đưa phương trình về dạng phương trình tích. - Giải phương trình lượng giác cơ bản. - Tìm các nghiệm thỏa mãn \(0 < x < \pi \). Cách giải: Ta có \({\cos ^2}x - \cos x = 0 \Leftrightarrow \cos x\left( {\cos x - 1} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\\cos x = 1\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\). + Xét họ nghiệm \(x = \dfrac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Ta có: \(0 < x < \pi \Rightarrow 0 < \dfrac{\pi }{2} + k\pi < \pi \)\( \Leftrightarrow - \dfrac{1}{2} < k < \dfrac{1}{2}\). Mà \(k \in \mathbb{Z} \Rightarrow k = 0 \Rightarrow x = \dfrac{\pi }{2}\). + Xét họ nghiệm \(x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Ta có: \(0 < x < \pi \Rightarrow 0 < k2\pi < \pi \)\( \Leftrightarrow 0 < k < \dfrac{1}{2}\). Mà \(k \in \mathbb{Z} \Rightarrow k \in \emptyset \). Vậy phương trình đã cho có duy nhất 1 nghiệm thỏa mãn là \(x = \dfrac{\pi }{2}\). Chọn C. Câu 16: Phương pháp: - Tìm ĐKXĐ của phương trình. - Sử dụng công thức \(\cot x = \dfrac{1}{{\tan x}}\). - Giải phương trình tìm \(\tan x\), sau đó giải phương trình lượng giác cơ bản \(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Cách giải: ĐKXĐ: \(\left\{ \begin{array}{l}\sin x \ne 0\\\cos x \ne 0\end{array} \right. \Leftrightarrow \sin 2x \ne 0\)\( \Leftrightarrow x \ne \dfrac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\). Ta có \(\begin{array}{l}\tan x = \cot x \Leftrightarrow \tan x = \dfrac{1}{{\tan x}}\\ \Leftrightarrow {\tan ^2}x = 1\\ \Leftrightarrow \tan x = \pm 1\\ \Leftrightarrow x = \pm \dfrac{\pi }{4} + k\pi \\ = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn D. Câu 17: Phương pháp: Áp dụng công thức tính thể tích khối chóp có chiều cao \(h\), diện tích đáy \(B\) là \(V = \dfrac{1}{3}Bh\). Cách giải: Ta có \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}}\)\( = \dfrac{1}{3}.a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\). Chọn A. Câu 18: Phương pháp: - Sử dụng định lí: \(a\parallel b \Rightarrow \angle \left( {a;c} \right) = \angle \left( {b;c} \right)\). - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Cách giải: Ta có \(AB\parallel CD\) \( \Rightarrow \angle \left( {SB;CD} \right) = \angle \left( {SB;AB} \right) = \angle SBA\). Xét \(\Delta SAB\) vuông tại \(A\) có: \(\tan \angle SBA = \dfrac{{SA}}{{AB}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 \)\( \Rightarrow \angle SBA = {60^0}\). Vậy \(\angle \left( {SB;CD} \right) = {60^0}\). Chọn A. Câu 19: Phương pháp: Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có TCN \(y = \dfrac{a}{c}\) và TCĐ \(x = - \dfrac{d}{c}\). Cách giải: Hàm số \(y = \dfrac{{3x - 1}}{{x - 3}}\) có \(x = 3\) là tiệm cận đứng và \(y = 3\) là tiệm cận ngang. Chọn B. Câu 20: Phương pháp: Sử dụng các công thức tính tổ hợp, chỉnh hợp. Cách giải: Cả 3 khối có tất cả \(13 + 12 + 12 = 37\) (học sinh). Số cách chọn 2 học sinh bất kì là: \(C_{37}^2\) cách. Gọi A là biến cố: “Chọn 2 học sinh không cùng khối” \( \Rightarrow \overline A \): “Chọn 2 học sinh cùng khối”. Số cách chọn 2 học sinh cùng khối là \(C_{13}^2 + C_{12}^2 + C_{12}^2\) (cách) \( \Rightarrow n\left( {\overline A } \right) = C_{13}^2 + C_{12}^2 + C_{12}^2\) Vậy xác suất của biến cố A là \(P\left( A \right) = 1 - \dfrac{{C_{13}^2 + C_{12}^2 + C_{12}^2}}{{C_{37}^2}} = \dfrac{{76}}{{111}}\). Chọn A. Câu 21: Phương pháp: - Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. - Sử dụng tỉ số lượng giác để tính góc. Cách giải: Gọi \(M\) là trung điểm của \(BC\). Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AM \bot BC\) và \(AM = \dfrac{1}{2}BC = a\). Ta có: \(\left\{ \begin{array}{l}BC \bot AM\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right)\)\( \Rightarrow BC \bot SM\). \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SM \subset \left( {SBC} \right),\,\,SM \bot BC\\AM \subset \left( {ABC} \right),\,\,AM \bot BC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SM;AM} \right)\)\( = \angle SMA\). Xét tam giác vuông \(SAM\) có: \(\tan \angle SMA = \dfrac{{SA}}{{AM}} = \dfrac{a}{a} = 1 \Rightarrow \angle SMA = {45^0}\). Vậy \(\angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = {45^0}\). Chọn A. Câu 22: Phương pháp: Tìm đạo hàm và tìm cực trị của hàm số. Cách giải: Ta có \(y = - {x^4} + 4{x^2} + 2019\)\( \Rightarrow y' = - 4{x^3} + 8x = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right. \Rightarrow {x_1} + {x_2} + {x_3} = 0\). Chọn A. Câu 23: Phương pháp: - Tính đạo hàm của hàm số, giải phương trình \(y' = 0\) xác định các nghiệm \({x_i} \in \left[ {0;4} \right]\). - Tính các giá trị: \(y\left( {{x_i}} \right);\,\,y\left( 0 \right);\,\,y\left( 4 \right)\). - Kết luận: \(\mathop {max}\limits_{\left[ {0;4} \right]} y = \max \left\{ {y\left( {{x_i}} \right);\,\,y\left( 0 \right);\,\,y\left( 4 \right)} \right\}\), \(\mathop {min}\limits_{\left[ {0;4} \right]} y = \min \left\{ {y\left( {{x_i}} \right);\,\,y\left( 0 \right);\,\,y\left( 4 \right)} \right\}\). Cách giải: Ta có \(y = {x^3} - 3{x^2} - 9x + 1\)\( \Rightarrow y' = 3{x^2} - 6x - 9 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1 \notin \left[ {0;4} \right]\\x = 3 \in \left[ {0;4} \right]\end{array} \right.\) Bảng biến thiên: Dựa vào bảng ta thấy giá trị lớn nhất \(M = 1\); giá trị nhỏ nhất \(m = - 26\). Vậy \(m + 2M = - 24\). Chọn D. Câu 24: Phương pháp: - Áp dụng công thức SHTQ của cấp số nhân có số hạng đầu \({u_1}\), công bội \(q\) là \({u_n} = {u_1}{q^{n - 1}}\). - Giải hệ phương trình 2 ẩn. Cách giải: Gọi công bội của CSN là \(q\) ta có \(\left\{ \begin{array}{l}{u_1} - {u_3} + {u_5} = 65\\{u_1} + {u_7} = 325\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{u_1} - {u_1}.{q^2} + {u_1}.{q^4} = 65\\{u_1} + {u_1}.{q^6} = 325\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{1 + {q^6}}}{{1 - {q^2} + {q^4}}} = 5\\{u_1} + {u_1}.{q^6} = 325\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{\left( {1 + {q^2}} \right)\left( {1 - {q^2} + {q^4}} \right)}}{{1 - {q^2} + {q^4}}} = 5\\{u_1} + {u_1}{q^6} = 325\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}1 + {q^2} = 5\\{u_1} + {u_1}{q^6} = 325\end{array} \right. \Leftrightarrow q = \pm 2\). \( \Rightarrow {u_1} + {u_1}.64 = 325 \Leftrightarrow {u_1} = 5\). Vậy \({u_3} = {u_1}.{q^2} = {5.2^2} = 20\). Chọn D. Câu 25: Phương pháp: - Áp dụng công thức tính tổ hợp: \(C_n^k = \dfrac{{n!}}{{k!\left( {n - k} \right)!}}\). - Giải phương trình tìm \(n\). Cách giải: Xét SHTQ: \(\begin{array}{l}k\dfrac{{C_n^k}}{{C_n^{k - 1}}}\\ = k.\dfrac{{n!}}{{k!\left( {n - k} \right)!}}.\dfrac{{\left( {k - 1} \right)!\left( {n - k + 1} \right)!}}{{n!}}\\ = k.\dfrac{{n - k + 1}}{k} = n - k + 1\end{array}\) Khi đó ta có: \(C_n^1 + 2\dfrac{{C_n^2}}{{C_n^1}} + ... + n\dfrac{{C_n^n}}{{C_n^{n - 1}}} = 45\) \(\begin{array}{l} \Leftrightarrow n + \left( {n - 1} \right) + \left( {n - 2} \right)\\ + ... + \left( {n - \left( {n - 1} \right)} \right) = 45\\ \Leftrightarrow n.n - \left( {1 + 2 + 3 + ... + n - 1} \right)\\ = 45\\ \Leftrightarrow {n^2} - \dfrac{{n\left( {n - 1} \right)}}{2} = 45\\ \Leftrightarrow 2{n^2} - {n^2} + n = 90\\ \Leftrightarrow n = 9\end{array}\) Khi đó \(C_{n + 4}^n = C_{13}^9 = 715\) Chọn A. Câu 26: Phương pháp: Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) đồng biến trên \(\left( {a;b} \right) \Leftrightarrow \left\{ \begin{array}{l}y' > 0\\ - \dfrac{d}{c} \notin \left( {a;b} \right)\end{array} \right.\). Cách giải: TXĐ: \(D = \mathbb{R}\backslash \left\{ { - m} \right\}\). Ta có \(y = \dfrac{{x - 1}}{{x + m}} \Rightarrow y' = \dfrac{{m + 1}}{{{{\left( {x + m} \right)}^2}}}\). Để hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) khi \(\left\{ \begin{array}{l}y' = \dfrac{{m + 1}}{{{{\left( {x + m} \right)}^2}}} > 0\\ - m \notin \left( {0; + \infty } \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > - 1\\ - m \le 0\end{array} \right. \Leftrightarrow m \ge 0\). Vậy \(m \in \left[ {0; + \infty } \right)\). Chọn B. Câu 27: Phương pháp: - Tính \(y'\). - Tìm điều kiện để phương trình \(y' = 0\) có 2 nghiệm phân biệt. - Hàm đa thức bậc ba \(y = a{x^3} + b{x^2} + cx + d\) có 2 điểm cực tiểu và \(a > 0\) thì \({x_{CT}} > {x_{CD}}\). - Giải phương trình \({x_{CT}} > 0\) tìm \(m\). Cách giải: TXĐ: \(D = \mathbb{R}\). Ta có: \(y' = 3{x^2} + 2x + m\). Để hàm số có 2 điểm cực trị thì phương trình \(y' = 0\) phải có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = 1 - 3m > 0 \Leftrightarrow m < \dfrac{1}{3}\) Khi đó ta có \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = \dfrac{{ - 1 + \sqrt {1 - 3m} }}{3}\\{x_2} = \dfrac{{ - 1 - \sqrt {1 - 3m} }}{3}\end{array} \right.\). Vì hàm số \(y = {x^3} + {x^2} + mx - 1\) có hệ số \(a = 1 > 0\) nên \({x_{CT}} > {x_{CD}}\), do đó \({x_{CT}} = {x_1} = \dfrac{{ - 1 + \sqrt {1 - 3m} }}{3}\). Theo bài ra ta có . \(\begin{array}{l}\dfrac{{ - 1 + \sqrt {1 - 3m} }}{3} > 0\\ \Leftrightarrow - 1 + \sqrt {1 - 3m} > 0\\ \Leftrightarrow \sqrt {1 - 3m} > 1\\ \Leftrightarrow 1 - 3m > 1 \Leftrightarrow m < 0\end{array}\) Kết hợp điều kiện ta có \(m < 0\). Chọn A. Câu 28: Phương pháp: Sử dụng công thức tính tổng \(1 + 2 + ... + n = \dfrac{{n\left( {n + 1} \right)}}{2}\). Cách giải: Thực hiện liên tiếp việc xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng sẽ là tổng của các số tự nhiên từ 1 đến 2020. Vậy số còn lại trên bảng là \(1 + 2 + ... + 2020 = \dfrac{{2020.2021}}{2}\)\( = 2041210\). Chọn B. Câu 29: Phương pháp: Chia cả 2 vế phương trình cho 2. Cách giải: Ta có \(\begin{array}{l}\,\,\,\,\,\,\sin 5x + \sqrt 3 \cos 5x = 2\sin 7x\\ \Leftrightarrow \dfrac{1}{2}\sin 5x + \dfrac{{\sqrt 3 }}{2}\cos 5x = \sin 7x\\ \Leftrightarrow \sin 5x\cos \dfrac{\pi }{3} + \cos 5x\sin \dfrac{\pi }{3} = \sin 7x\\ \Leftrightarrow \sin \left( {5x + \dfrac{\pi }{3}} \right) = \sin 7x\\ \Leftrightarrow \left[ \begin{array}{l}7x = 5x + \dfrac{\pi }{3} + k2\pi \\7x = - 5x + \dfrac{{2\pi }}{3} + m2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = \dfrac{\pi }{{18}} + \dfrac{{m\pi }}{6}\end{array} \right.\,\,\left( {k,\,\,m \in \mathbb{Z}} \right)\end{array}\) Mà \(x \in \left( {0;\dfrac{\pi }{2}} \right)\)\( \Rightarrow \left[ \begin{array}{l}0 < \dfrac{\pi }{6} + k\pi < \dfrac{\pi }{2}\\0 < \dfrac{\pi }{{18}} + \dfrac{{m\pi }}{6} < \dfrac{\pi }{2}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l} - \dfrac{1}{6} < k < \dfrac{1}{3}\\ - \dfrac{1}{3} < m < \dfrac{8}{3}\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}k = 0\\m \in \left\{ {0;1;2} \right\}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6}\\x \in \left\{ {\dfrac{\pi }{{18}};\dfrac{{2\pi }}{9};\dfrac{{7\pi }}{{18}}} \right\}\end{array} \right.\) Vậy phương trình đã cho có 4 nghiệm thỏa mãn. Chọn A. Câu 30: Phương pháp: Áp dụng tính chất của hàm đồng biến. Cách giải: Vì \(f'\left( x \right) > 0\,\,\forall x \in \mathbb{R}\) nên hàm số \(y = f\left( x \right)\) đồng biến trên \(\mathbb{R}\). Do đó ta có: \(\left\{ \begin{array}{l}f\left( 2 \right) > f\left( 1 \right) = 2\\f\left( 3 \right) > f\left( 1 \right) = 2\end{array} \right. \Rightarrow f\left( 2 \right) + f\left( 3 \right) > 4\), nên mệnh đề A sai. \(f\left( { - 1} \right) < f\left( 1 \right) = 2\) nên mệnh đề B sai. \(f\left( 2 \right) > f\left( 1 \right) = 2 \Rightarrow \) Mệnh đề C sai. Vì \(2018 < 2019 \Rightarrow f\left( {2018} \right) < f\left( {2019} \right)\) nên mệnh đề D đúng. Chọn D. Câu 31: Phương pháp: Xét các trường hợp. Cách giải: Gọi số có 4 chữ số là \(\overline {abcd} \,\,\left( {a \ne 0,\,\,a,b,c,d \in A} \right)\). Vì \(\overline {abcd} < 4012\) nên ta xét các TH sau: TH1: \(a = 4\). Để \(\overline {4bca} < 4012 \Rightarrow b \le 0 \Rightarrow b = 0\) \( \Rightarrow \) Số có dạng \(\overline {40cd} < 4012 \Rightarrow \overline {cd} < 12\). \( \Rightarrow c \le 1\). Mà \(c \ne b \Rightarrow c \ne 0\), do đó \(c = 1\). \( \Rightarrow \) Số có dạng \(\overline {401d} < 4012 \Rightarrow d < 2\). Mà \(d \ne b,\,\,d \ne c \Rightarrow d \notin \left\{ {0;1} \right\} \Rightarrow d \in \emptyset \). \( \Rightarrow \) TH1 không có số nào thỏa mãn. TH2: \(a \in \left\{ {1;3} \right\}\) \( \Rightarrow \) Có 2 cách chọn \(a\). Khi đó số \(\overline {abcd} \) chắc chắn thỏa mãn nhỏ hơn 4012. \(d \in \left\{ {0;2;4;6} \right\} \Rightarrow \) Có 4 cách chọn \(d\). Số cách chọn 2 chữ số còn lại là \(A_5^2 = 20\) cách. \( \Rightarrow TH2\) có \(2.4.20 = 160\) số. TH3: \(a = 2\) \( \Rightarrow \) Có 1 cách chọn \(a\). Khi đó số \(\overline {abcd} \) chắc chắn thỏa mãn nhỏ hơn 4012. \(d \in \left\{ {0;4;6} \right\}\,\,\left( {d \ne a} \right) \Rightarrow \) Có 3 cách chọn \(d\). Số cách chọn 2 chữ số còn lại là \(A_5^2 = 20\) cách. \( \Rightarrow TH3\) có \(1.3.20 = 60\) số. Vậy tổng có \(160 + 60 = 220\) số. Chọn D. Câu 32: Phương pháp: - Tìm đạo hàm của phương trình quãng đường để suy ra v. - Tìm vận tốc lớn nhất bằng cách sử dụng hằng đẳng thức. Cách giải: Ta có \(v = s' = - \dfrac{3}{2}{t^2} + 18t\). Ta có: \(v = - \dfrac{3}{2}\left( {{t^2} - 12t} \right) = - \dfrac{3}{2}\left[ {{{\left( {t - 6} \right)}^2} - 36} \right]\)\( = - \dfrac{3}{2}{\left( {t - 6} \right)^2} + 54 \le 54\). Vậy \({v_{\max }} = 54\,\,\left( {m/s} \right) \Leftrightarrow t = 6\,\,\left( s \right)\). Chọn C. Câu 33: Phương pháp: Hàm số \(y = f\left( x \right)\) đạt cực đại tại \(x = {x_0} \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.\). Cách giải: Ta có \(y = \left( {m - 1} \right){x^4}\) \( \Rightarrow y' = 4\left( {m - 1} \right){x^3} = 0 \Leftrightarrow x = 0\). Để hàm số đạt cực đại tại \(x = 0\) thì qua điểm \(x = 0\) đạo hàm phải đổi dấu từ dương sang âm. \( \Rightarrow \left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ - }} y > 0\\\mathop {\lim }\limits_{x \to {0^ + }} y < 0\end{array} \right. \Leftrightarrow m - 1 < 0\)\( \Leftrightarrow m < 1\). Chọn A. Câu 34: Phương pháp: Áp dụng công thức tính nhân xác suất. Cách giải: Khi gieo hai con súc sắc trong một lần gieo thì có tất cả \(6.6 = 36\) khả năng. Ta có \(6 = 1 + 5 = 2 + 4 = 3 + 3 = 4 + 2 = 5 + 1\). Xác suất để số chấm xuất hiện trên 2 con súc sắc bằng 6 là \(\dfrac{5}{{36}}\), xác suất để số chấm xuất hiện trên 2 con xúc xắc khác 6 là \(1 - \dfrac{5}{{36}}\). Vậy xác suất cần tìm là: \(P = C_3^1.\left( {\dfrac{5}{{36}}} \right).{\left( {1 - \dfrac{5}{{36}}} \right)^2} \approx 0,309\). Chọn D. Câu 35: Phương pháp: Khai triển nhị thức Niton: \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}} \). Cách giải: Ta có \(\begin{array}{l}{\left( {1 - 2x - 3{x^2}} \right)^9}\\ = \sum\limits_{k = 0}^9 {C_9^k.{{\left( {1 - 2x} \right)}^k}.{{\left( { - 3{x^2}} \right)}^{9 - k}}} \\{\left( {1 - 2x - 3{x^2}} \right)^9}\\ = \sum\limits_{k = 0}^9 {C_9^k.{{\left( { - 3} \right)}^{9 - k}}} {x^{18 - 2k}}.\sum\limits_{m = 0}^k {C_k^m.{{\left( { - 2x} \right)}^m}} \\{\left( {1 - 2x - 3{x^2}} \right)^9}\\ = \sum\limits_{k = 0}^9 {\sum\limits_{m = 0}^k {C_9^k.{{\left( { - 3} \right)}^{9 - k}}C_k^m.{{\left( { - 2} \right)}^m}.{x^{18 - 2k + m}}} } \end{array}\) Số hạng chứa \({x^5}\) trong khai triển ứng với \(18 - 2k + m = 5 \Leftrightarrow 2k - m = 13\) \(\left( {m,\,\,k \in \mathbb{Z},\,\,0 \le m \le k \le 9} \right)\). \( \Rightarrow \left[ \begin{array}{l}k = 7;m = 1\\k = 8;m = 3\\k = 9;m = 5\end{array} \right.\) Khi đó hệ số của \({x^5}\) bằng \(C_9^7.{\left( { - 3} \right)^2}.C_7^1{\left( { - 2} \right)^1}\)\( + C_9^8.{\left( { - 3} \right)^1}.C_8^3.{\left( { - 2} \right)^3}\)\( + C_9^9.{\left( { - 3} \right)^0}.C_9^5.{\left( { - 2} \right)^5} = 3528\). Chọn C. Câu 36: Phương pháp: Áp dụng định nghĩa khối đa diện. Cách giải: Khối đa diện lồi có 10 đỉnh và 7 mặt thì áp dụng định lí ơle ta có \( \Rightarrow 10 - C + 7 = 2 \Rightarrow C = 15\). Chọn C. Câu 37: Phương pháp: +) Xác định mặt phẳng đi qua \(AG\) và song song với BC. +) Sử dụng công thức tỉ lệ thể tích Simpson: Choc chóp \(S.ABC\), \(A' \in SA,\,\,B' \in SB,\,\,C' \in SC\). Khi đó \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\). Cách giải: Trong \(\left( {SBC} \right)\) qua \(G\) kẻ \(MN//BC{\mkern 1mu} {\mkern 1mu} \left( {M \in SB,{\mkern 1mu} {\mkern 1mu} N \in SC} \right)\). Khi đó mặt phẳng đi qua AG và song song với BC chính là mặt phẳng \(\left( {AMN} \right)\). Mặt phẳng này chia khối chóp thành 2 khối S.AMN và AMNBC. Gọi \(H\) là trung điểm của \(BC\). Vì \(MN//BC \Rightarrow \) Theo định lí Ta-lét ta có: \(\dfrac{{SM}}{{SB}} = \dfrac{{SN}}{{SC}} = \dfrac{2}{3}\left( { = \dfrac{{SG}}{{SH}}} \right)\). \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{2}{3}.\dfrac{2}{3} = \dfrac{4}{9}\)\( \Rightarrow {V_{S.AMN}} = \dfrac{4}{9}{V_{S.ABC}}\). Mà \({V_{S.AMN}} + {V_{AMNBC}} = {V_{S.ABC}} \Rightarrow {V_{AMNBC}} = \dfrac{5}{9}{V_{S.ABC}} = V\). Ta có \(\Delta ABC\) vuông cân tại \(B \Rightarrow AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = a\)\( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}{a^2}\). \( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}}\)\( = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\). Vậy \(V = \dfrac{5}{9}.\dfrac{{{a^3}}}{6} = \dfrac{{5{a^3}}}{{54}}\). Chọn A. Câu 38: Phương pháp: Dựng hình và đổi điểm trong bài toán khoảng cách từ điểm đến mặt phẳng Cách giải: Gọi \(I\) là trung điểm của \(MC \Rightarrow BI \bot MC\;\)(vì \(\Delta BMC\) vuông cân). Kẻ \(BH \bot B'I \Rightarrow BH \bot \left( {B'MC} \right)\)\( \Rightarrow d\left( {B,\left( {B'MC} \right)} \right) = BH.\) Ta có tam giác \(BMC\) vuông cân tại \(B\) nên \(BI = \dfrac{{MC}}{2} = \dfrac{{a\sqrt 2 }}{2}\) \(BH = \dfrac{{BB'.BI}}{{\sqrt {B{{B'}^2} + B{I^2}} }} = \dfrac{{a\sqrt {21} }}{7}\)\( \Rightarrow d\left( {B,\left( {MB'C} \right)} \right) = \dfrac{{a\sqrt {21} }}{7}.\) Mặt khác gọi \(E\) là giao điểm của \(BD\) và \(MC \Rightarrow \dfrac{{d\left( {D,\left( {MB'C} \right)} \right)}}{{d\left( {B,\left( {MB'C} \right)} \right)}} = \dfrac{{ED}}{{EB}}\)\( = \dfrac{{DC}}{{MB}} = 2.\) \( \Rightarrow d\left( {D,\left( {MB'C} \right)} \right) = 2d\left( {B,\left( {MB'C} \right)} \right) = \dfrac{{2a\sqrt {21} }}{7}.\) Chọn D. Câu 39: Phương pháp: Xác định chiều cao hình chóp \(\left\{ {\begin{array}{*{20}{l}}{\left( P \right) \bot \left( Q \right)}\\{\left( P \right) \cap \left( Q \right) = d}\\{a \bot d;{\mkern 1mu} a \subset \left( P \right)}\end{array}} \right. \Rightarrow a \bot \left( Q \right)\) Thể tích khối chóp là \(V = \dfrac{1}{3}h.S\) với \(h\) là chiều cao hình chóp và \(S\) là diện tích đáy. Cách giải: Trong \(\left( {SAB} \right)\) kẻ \(SH \bot AB\) tại \(H\) Ta có \(\left\{ {\begin{array}{*{20}{l}}{\left( {SAB} \right) \bot \left( {ABCD} \right)}\\{\left( {SAB} \right) \cap \left( {ABCD} \right) = AB}\\{SH \bot AB;{\mkern 1mu} SH \subset \left( {SAB} \right)}\end{array}} \right.\)\( \Rightarrow SH \bot \left( {ABCD} \right)\) Xét tam giác SAH có \(SH = SA.\sin \widehat {SAH} = 2a.\sin {30^0} = a\) Thể tích khối chóp là \(V = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}a.{a^2} = \dfrac{{{a^3}}}{3}.\) Chọn D. Câu 40: Phương pháp: - Dựa vào định nghĩa để xác định các đường tiệm cận của đồ thị hàm số \(y = f\left( x \right)\). + Đường thẳng \(y = {y_0}\) là đường tiệm cận ngang của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } y = {y_0}\), \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } y = {y_0}\). + Đường thẳng \(x = {x_0}\) là đường tiệm cận đứng của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to x_0^ + } y = {\rm{\;}} + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ + } y = {\rm{\;}} - \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = {\rm{\;}} + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = {\rm{\;}} - \infty \). Cách giải: Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \dfrac{{\left| x \right| - 2018}}{{x + 2019}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x - 2018}}{{x + 2019}} = 1\\\mathop {\lim }\limits_{x \to - \infty } \dfrac{{\left| x \right| - 2018}}{{x + 2019}} = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{ - x - 2018}}{{x + 2019}} = - 1\end{array}\) Vậy đồ thị hàm số có hai đường tiệm cận ngang là \(y = \pm 1\). Chọn C. Câu 41: Phương pháp: Sử dụng công thức \({V_{AMNP}} = {V_{P.AMN}}\)\( = \dfrac{1}{3}d\left( {P;\left( {AMN} \right)} \right).{S_{AMN}}\). Cách giải: Ta có \({V_{AMNP}} = {V_{P.AMN}}\)\( = \dfrac{1}{3}d\left( {P;\left( {AMN} \right)} \right).{S_{AMN}}\)\( = \dfrac{1}{3}d\left( {P;\left( {SAB} \right)} \right).{S_{AMN}}\). Do \(CP\parallel \left( {SAB} \right) \Rightarrow d\left( {P;\left( {SAB} \right)} \right)\)\( = d\left( {C;\left( {SAB} \right)} \right)\). Lại có \({S_{AMN}} = \dfrac{1}{2}d\left( {N;AM} \right).AM\)\( = \dfrac{1}{2}.\dfrac{1}{2}d\left( {B;SA} \right).\dfrac{1}{2}SA = \dfrac{1}{4}{S_{SAB}}\) \( \Rightarrow {V_{AMNP}} = \dfrac{1}{3}.d\left( {C;\left( {SAB} \right)} \right).\dfrac{1}{4}.{S_{SAB}} = \dfrac{1}{4}{V_{C.SAB}}\). Ta có \({V_{C.SAB}} = {V_{S.ABC}} = \dfrac{1}{3}d\left( {S;\left( {ABC} \right)} \right).{S_{ABC}}\)\( = \dfrac{1}{3}d\left( {S;\left( {ABC} \right)} \right).\dfrac{1}{2}{S_{ABCD}}\)\( = \dfrac{1}{2}{V_{S.ABCD}} = \dfrac{V}{2}\). Vậy \({V_{AMNP}} = \dfrac{V}{8}\). Chọn A. Câu 42: Phương pháp: - Hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) tiếp xúc với nhau khi và chỉ khi hệ phương trình \(\left\{ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f'\left( x \right) = g'\left( x \right)\end{array} \right.\) có nghiệm. - Nghiệm của phương trình \(f\left( x \right) = m\) là hoành độ giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và \(y = m\). Cách giải: Đồ thị hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) tiếp xúc với trục hoành \(y = 0\) tại gốc tọa độ. \( \Rightarrow \left\{ \begin{array}{l}{x^3} + a{x^2} + bx + c = 0\\3{x^2} + 2ax + b = 0\end{array} \right.\) có nghiệm \(x = 0\) \( \Rightarrow \left\{ \begin{array}{l}c = 0\\b = 0\end{array} \right.\) \( \Rightarrow f\left( x \right) = {x^3} + a{x^2}\). Đồ thị hàm số cắt đường thẳng \(x = 1\) tại điểm có tung độ bằng 3 nên đồ thị hàm số đi qua điểm \(A\left( {1;3} \right)\). \( \Rightarrow 3 = {1^3} + a{.1^2} \Leftrightarrow a = 2\). Vậy \(a = 2,\,b = c = 0\). Chọn C. Câu 43: Phương pháp: - Xác định hình chiếu của điểm B lên (SAC). - Góc giữa SB và (SAC) là góc giữa SB và hình chiếu của SB lên (SAC). - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc. Cách giải: Gọi \(AC = BD = \left\{ O \right\}\). Vì \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{BD \bot SA}\end{array}} \right. \Rightarrow BD \bot \left( {SAC} \right)\)\( \Rightarrow BO \bot \left( {SAC} \right)\). \( \Rightarrow SO\) là hình chiếu của SB lên \(\left( {SAC} \right)\). \( \Rightarrow \angle \left( {SB;\left( {SAC} \right)} \right) = \angle \left( {SB;SO} \right) = \angle BSO\). Vì ABCD là hình vuông cạnh 2a nên \(BD = 2a\sqrt 2 {\rm{\;}} \Rightarrow BO = \dfrac{1}{2}BD = a\sqrt 2 \). Áp dụng định lí Pytago trong tam giác vuông SAB ta có: \(SB = \sqrt {S{A^2} + A{B^2}} {\rm{\;}} = 2a\sqrt 2 \). Vì \(BO \bot \left( {SAC} \right) \Rightarrow BO \bot SO \Rightarrow \Delta SOB\) vuông tại \(O\). \( \Rightarrow \sin \angle BSO = \dfrac{{BO}}{{SB}} = \dfrac{{a\sqrt 2 }}{{2a\sqrt 2 }} = \dfrac{1}{2}\) \( \Rightarrow \angle BSO = {30^0}\). Vậy \(\angle \left( {SB;\left( {SAC} \right)} \right) = {30^0}\). Chọn D. Câu 44: Phương pháp: Hai đường thẳng vuông góc với nhau khi và chỉ khi tích hệ số góc của hai đường thẳng đó bằng \( - 1\). Cách giải: \(y = \dfrac{{{x^3}}}{3} - \dfrac{{{x^2}}}{2} + x + 1 \Rightarrow y' = {x^2} - x + 1\) Gọi \(A\left( {{x_1};{y_1}} \right),{\mkern 1mu} {\mkern 1mu} B\left( {{x_2};{y_2}} \right)\) là 2 điểm trên đồ thị hàm số \(y = \dfrac{{{x^3}}}{3} - \dfrac{{{x^2}}}{2} + x + 1\) sao cho từ tiếp tuyến tại A và tại B vuông góc với nhau. Khi đó: \(y'\left( {{x_1}} \right).y'\left( {{x_2}} \right) = {\rm{\;}} - 1\) \( \Leftrightarrow \left( {{x_1}^2 - {x_1} + 1} \right)\left( {{x_2}^2 - {x_2} + 1} \right) = {\rm{\;}} - 1\) : Vô lý, do \({x_1}^2 - {x_1} + 1,{\mkern 1mu} {\mkern 1mu} {x_2}^2 - {x_2} + 1 > 0,{\mkern 1mu} {\mkern 1mu} \forall {x_1},{x_2}\) Vậy, không tồn tại tiếp điểm A, B thỏa mãn đề bài, suy ra, không tồn tại điểm mà từ đó kẻ được hai tiếp tuyến đến đồ thị hàm số \(y = \dfrac{{{x^3}}}{3} - \dfrac{{{x^2}}}{2} + x + 1\) sao cho hai tiếp tuyến này vuông góc với nhau. Chọn A. Câu 45: Phương pháp: So sánh chiều cao và diện tích đáy với hình lăng trụ. Cách giải: Ta có: \(\begin{array}{l}{V_{MACC'}} = {V_{A.CC'M}}\\ = \dfrac{1}{3}d\left( {A;\left( {BCC'B'} \right)} \right).{S_{CC'M}}\end{array}\) \( = \dfrac{1}{3}d\left( {A;\left( {BCC'B'} \right)} \right)\)\(.\dfrac{1}{2}d\left( {M;CC'} \right).CC'\) \( = \dfrac{1}{6}d\left( {A;\left( {BCC'B'} \right)} \right).{S_{BCC'B'}}\)\( = \dfrac{1}{2}{V_{A.BCC'B'}} = \dfrac{1}{2}.\dfrac{2}{3}{V_{ABC.A'B'C'}}\)\( = \dfrac{1}{3}{V_{ABC.A'B'C'}}\) Tam giác \(ABC\) cân tại \(C\) có \(\angle BAC = {30^0} = \angle ABC\)\( \Rightarrow \angle ACB = {120^0}\). Áp dụng định lí Sin trong tam giác \(ABC\) ta có: \(\dfrac{{AC}}{{\sin B}} = \dfrac{{AB}}{{\sin C}}\)\( \Leftrightarrow AC = \dfrac{{AB\sin B}}{{\sin C}}\)\( = \dfrac{{a\sqrt 3 .\sin {{30}^0}}}{{\sin {{120}^0}}} = a\). Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC\)\( = \dfrac{1}{2}.a\sqrt 3 .a.\sin {30^0} = \dfrac{{{a^2}\sqrt 3 }}{4}\). \( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}}\)\( = a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{4}\). Vậy \({V_{MACC'}} = \dfrac{1}{3}{V_{ABC.A'B'C'}} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\). Chọn A. Câu 46: Phương pháp: +) Dùng công thức đạo hàm hàm hợp tính \(g'\left( x \right)\) với \(y = g\left( x \right) = {\left( {f\left( {3 - x} \right)} \right)^2}\) +) Hàm số \(y = g\left( x \right)\) nghịch biến trên \(\left( {a;b} \right) \Leftrightarrow g'\left( x \right) \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm. Cách giải: Dựa vào bảng xét dấu \(f'\left( x \right)\) ta suy ra BBT của hàm số \(y = f\left( x \right)\) như sau: \( \Rightarrow f\left( x \right) \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}\). Đặt \(y = g\left( x \right) = {\left( {f\left( {3 - x} \right)} \right)^2}\)\( \Rightarrow g'\left( x \right) = {\rm{\;}} - 2f\left( {3 - x} \right).f'\left( {3 - x} \right) \le 0\). Với \(x = 4\)\( \Rightarrow g'\left( 4 \right) = {\rm{\;}} - 2f\left( { - 1} \right)f'\left( { - 1} \right) < 0 \Rightarrow \) Loại đáp án C và D. Với \(x = 6\)\( \Rightarrow g'\left( 6 \right) = {\rm{\;}} - 2f\left( { - 3} \right)f'\left( { - 3} \right) > 0 \Rightarrow \) Loại đáp án B. Chọn A. Câu 47: Phương pháp: - Phá trị tuyệt đối và giải phương trình. - Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) song song với trục hoành. Cách giải: Ta có \(2\left| {f\left( {2x - 3} \right)} \right| - 5 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}f\left( {2x - 3} \right) = \dfrac{5}{2}\\f\left( {2x - 3} \right) = - \dfrac{5}{2}\end{array} \right.\). Dựa vào BBT ta có: \(\left[ \begin{array}{l}2x - 3 = a < 0\\2x - 3 = b > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{a + 3}}{2}\\x = \dfrac{{b + 3}}{2}\end{array} \right.\). Vậy phương trình ban đầu có 2 nghiệm phân biệt. Chọn B. Câu 48: Phương pháp: - Dựa vào định nghĩa để xác định các đường tiệm cận của đồ thị hàm số \(y = f\left( x \right)\). + Đường thẳng \(y = {y_0}\) là đường tiệm cận ngang của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } y = {y_0}\), \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } y = {y_0}\). + Đường thẳng \(x = {x_0}\) là đường tiệm cận đứng của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to x_0^ + } y = {\rm{\;}} + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ + } y = {\rm{\;}} - \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = {\rm{\;}} + \infty \), \(\mathop {\lim }\limits_{x \to x_0^ - } y = {\rm{\;}} - \infty \). Cách giải: Hàm số \(y = \dfrac{{\sqrt {4{x^2} + 5} }}{{\sqrt {2x + 1} - x - 1}}\) có ĐKXĐ: \(x \ge - \dfrac{1}{2};x \ne 0\). Ta có \(y = \dfrac{{\sqrt {4{x^2} + 5} \left( {\sqrt {2x + 1} + x + 1} \right)}}{{ - {x^2}}}\) nhận đường thẳng \(x = 0\) làm tiệm cận đứng. Ta lại có: \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {4{x^2} + 5} \left( {\sqrt {2x + 1} + x + 1} \right)}}{{ - {x^2}}}\)\( = - 2\) nên đồ thị hàm số có tiệm cận ngang là \(y = 2\). Vậy đồ thị hàm số đã cho có tất cả 2 đường tiệm cận. Chọn C. Câu 49: Phương pháp: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến. Gọi E là trung điểm của AD ta có ABCE là hình vuông \( \Rightarrow CE \bot AD\) và \(CE = a\) \(\left\{ \begin{array}{l}CE \bot AD\\CE \bot SA\end{array} \right. \Rightarrow CE \bot \left( {SAD} \right)\)\( \Rightarrow CE \bot SD\) Kẻ \(EH \bot SD{\mkern 1mu} {\mkern 1mu} \left( {H \in SD} \right)\) ta có \(\left\{ \begin{array}{l}SD \bot EH\\SD \bot CE\end{array} \right. \Rightarrow SD \bot \left( {HCE} \right)\)\( \Rightarrow SD \bot CH\) \(\left\{ \begin{array}{l}\left( {SAD} \right) \cap \left( {SCD} \right) = SD\\\left( {SAD} \right) \supset EH \bot CD\\\left( {SCD} \right) \supset CH \bot CD\end{array} \right.\)\( \Rightarrow \widehat {\left( {\left( {SAD} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {EH;CH} \right)}\) Ta có:
\( \Rightarrow HE = \dfrac{{a\sqrt 2 .a}}{{\sqrt {2{a^2} + 4{a^2}} }} = \dfrac{{a\sqrt 3 }}{3}\) Xét tam giác SCD có \(CE = AE = ED = a\)\( \Rightarrow CE = \dfrac{1}{2}AD \Rightarrow \Delta ACD\) vuông tại C. Có \(\left\{ \begin{array}{l}CD \bot AC\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right)\)\( \Rightarrow CD \bot SC \Rightarrow \Delta SCD\) vuông ở C. \( \Rightarrow CH = \dfrac{{SC.CD}}{{\sqrt {S{C^2} + C{D^2}} }}\)\( = \dfrac{{\sqrt {2{a^2} + 2{a^2}} .a\sqrt 2 }}{{\sqrt {2{a^2} + 2{a^2} + 2{a^2}} }} = \dfrac{{2\sqrt 3 a}}{3}\) Áp dụng định lí Cosin trong tam giác HCE: \(\cos \angle CHE = \dfrac{{E{H^2} + C{H^2} - C{E^2}}}{{2EH.CH}}\)\( = \dfrac{1}{2} \Rightarrow \angle CHE = {60^0}\) Vậy \(\widehat {\left( {\left( {SAD} \right);\left( {SCD} \right)} \right)} = {60^0}\). Chọn A. Câu 50: Phương pháp: - Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left[ {1; + \infty } \right) \Leftrightarrow y' \le 0\,\,\forall x \in \left[ {1; + \infty } \right)\). - Cô lập \(m\), đưa bất phương trình về dạng \(m \le g\left( x \right)\,\,\forall x \in \left[ {1; + \infty } \right)\)\( \Leftrightarrow m \le \mathop {\min }\limits_{\left[ {1; + \infty } \right)} g\left( x \right)\). - Lập BBT hàm số \(g\left( x \right)\) và kết luận. Cách giải: Hàm số đã cho xác định và liên tục trên \(\left[ {1; + \infty } \right)\). Ta có: \(y' = m{x^2} + 14mx + 14\). Để hàm số nghịch biến trên \(\left[ {1; + \infty } \right) \Leftrightarrow y' \le 0\,\,\forall x \in \left[ {1; + \infty } \right)\). \(\begin{array}{l} \Leftrightarrow m{x^2} + 14mx + 14 \le 0\\\forall x \in \left[ {1; + \infty } \right)\\ \Leftrightarrow m\left( {{x^2} + 14x} \right) + 14 \le 0\\\forall x \in \left[ {1; + \infty } \right)\\ \Leftrightarrow m\left( {{x^2} + 14x} \right) \le - 14\\\forall x \in \left[ {1; + \infty } \right)\\ \Leftrightarrow m \le \dfrac{{ - 14}}{{{x^2} + 14x}} = g\left( x \right)\\\forall x \in \left[ {1; + \infty } \right)\,\,\left( * \right)\\\left( {Do{x^2} + 14x > 0\forall x \in \left[ {1; + \infty } \right)} \right)\end{array}\) Xét hàm số \(g\left( x \right) = \dfrac{{ - 14}}{{{x^2} + 14x}}\) trên \(\left[ {1; + \infty } \right)\) ta có: \(g'\left( x \right) = \dfrac{{14.\left( {2x + 14} \right)}}{{{{\left( {{x^2} + 14x} \right)}^2}}} = 0\)\( \Leftrightarrow x = - 7 \notin \left[ {1; + \infty } \right)\). \( \Rightarrow \) Hàm số \(g\left( x \right)\) đồng biến trên \(\left[ {1; + \infty } \right)\) \( \Rightarrow m \le \mathop {\min }\limits_{\left[ {1; + \infty } \right)} g\left( x \right) = g\left( 1 \right) = - \dfrac{{14}}{{15}}\). Do đó \(\left( * \right) \Leftrightarrow m \le - \dfrac{{14}}{{15}}\). Vậy \(m \in \left( { - \infty ; - \dfrac{{14}}{{15}}} \right]\). Chọn B. HocTot.Nam.Name.Vn
|