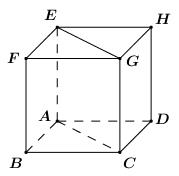
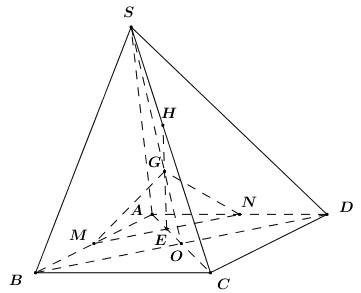
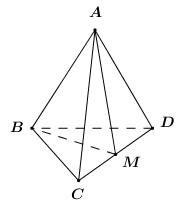
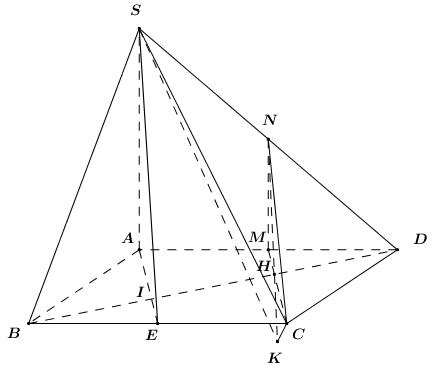
Đề kiểm tra giữa kì 2 Toán 11 - đề số 5 có lời giải chi tiết

Đề bài

Câu 1 . Cho \(a,\,\,b\) là hai số thực khác 0. Nếu \(\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} + ax + b}}{{x - 2}} = 6\) thì \(a + b\) bằng:

A. \(8\)        B. \(2\)        C. \( - 4\)     D. \( - 6\)

Câu 2 . Cho hình lập phương \(ABCD.EFGH\) có cạnh \(AB = a\). Khi đó \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng:

A. \({a^2}\sqrt 3 \)        B. \({a^2}\)

C. \({a^2}\sqrt 2 \)        D. \(\dfrac{{\sqrt 2 }}{2}{a^2}\)

Câu 3 .Trong các dãy số \(\left( {{u_n}} \right)\) sau đấy, dãy số nào không là cấp số cộng?

A. \(\left( {{u_n}} \right) = {\left( {n + 1} \right)^2} - {n^2}\)       

B. \({u_n} = 3n - 1\)     

C. \(\left\{ \begin{array}{l}{u_{n + 1}} = 2018 + {u_n}\\{u_1} = 3\end{array} \right.\)    

D. \({u_n} = {3^n} + 1\)

Câu 4. Cho \(a\) là một số thực khác 0. Tính \(\mathop {\lim }\limits_{x \to a} \dfrac{{{x^4} - {a^4}}}{{x - a}}\).

A. \(3{a^2}\)        B. \({a^3}\)         C. \(4{a^3}\)        D. \(2{a^3}\)

Câu 5 . Khẳng định nào sai trong các khẳng định sau:

A. Nếu \(a \bot \left( P \right),\,\,b//a\) thì \(b \bot \left( P \right)\)

B. Nếu \(a \bot \left( P \right),\,\,b//\left( P \right)\) thì \(a \bot b\)

C. Nếu \(\left( P \right)//\left( Q \right),\,\,a \bot \left( P \right)\) thì \(a \bot \left( Q \right)\)          

D. Nếu \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b,\,\,c \subset \left( P \right)\end{array} \right.\) thì \(a \bot \left( P \right)\)

Câu 6. Tính \(\lim \dfrac{{\left( {2{n^2} + 1} \right)n}}{{3 + n - 3{n^3}}}\).

A. \(\dfrac{2}{3}\)         B. \(0\)        C. \( - \dfrac{2}{3}\)      D. \( - \infty \)

Câu 7 . Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AD\) và \(G\) là trọng tâm tam giác \(SBD\). Mặt phẳng \(\left( {MNG} \right)\) cắt \(SC\) tại điểm \(H\). Tính \(\dfrac{{SH}}{{SC}}\).

A. \(\dfrac{2}{3}\)         B. \(\dfrac{2}{5}\)         C. \(\dfrac{1}{4}\)         D. \(\dfrac{1}{3}\)

Câu 8.Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?

A. \({u_n} = \dfrac{{2{n^3} - 11n + 1}}{{{n^2} - 2}}\)       

B. \({u_n} = \sqrt {{n^2} + 2n}  - n\)

C. \({u_n} = {3^n} + {2^n}\) 

D. \({u_n} = \dfrac{1}{{\sqrt {{n^2} - 2}  - \sqrt {{n^2} + 4} }}\)

Câu 9 . Mệnh đề nào dưới đây sai?

A. \(\mathop {\lim }\limits_{x \to  + \infty } \left( {4{x^2} - 7{x^3} + 2} \right) =  + \infty \)         

B. \(\mathop {\lim }\limits_{x \to  + \infty } \left( {5{x^3} - {x^2} + x + 1} \right) =  + \infty \)

C. \(\mathop {\lim }\limits_{x \to  - \infty } \left( {2{x^4} + 3x + 1} \right) =  + \infty \)     

D. \(\mathop {\lim }\limits_{x \to  - \infty } \left( {3x - {x^5} + 2} \right) =  + \infty \)

Câu 10 . Cho cấp số nhân \(\left( {{u_n}} \right)\) biết \({u_1} = 3,\,\,{u_2} =  - 6\). Khi đó \({u_5}\) bằng:

A. \(48\)      B. \( - 48\)   C. \( - 24\)   D. \(24\)

Câu 11 .Cho cấp số nhân lùi vô hạn \(1;\,\, - \dfrac{1}{2};\,\,\dfrac{1}{4};\,\, - \dfrac{1}{8};\,...;{\left( { - \dfrac{1}{2}} \right)^n},\,\,...\) có tổng là một phân số tối giản \(\dfrac{m}{n}\). Tính \(m + 2n\)

A. \(m + 2n = 5\)  B. \(m + 2n = 4\)

C. \(m + 2n = 7\)  D. \(m + 2n = 8\)

Câu 12 . Tính \(\lim \dfrac{{{{2018}^n} + {2^{2018}}}}{{{{2019}^n}}}\).

A. \(0\)        B. \( + \infty \)      C. \(1\)        D. \({2^{2018}}\)

Câu 13 . Cho tứ diện đều \(ABCD\). Số đo góc giữa hai đường thẳng \(AB\) và \(CD\) bằng:

A. \({60^0}\)        B. \({30^0}\)        C. \({90^0}\)        D. \({45^0}\)

Câu 14 . Tính \(\lim \left( {\sqrt {{n^2} + n}  - n} \right)\).

A. \(0\)        B. \(\dfrac{1}{2}\)         C. \( + \infty \)      D. \(1\)

Câu 15 .Cho hai số thực \(x,\,\,y\) thỏa mãn \(6,\,\,x,\,\, - 2,\,\,y\) lập thành cấp số cộng. Tìm \(x,\,\,y\).

A. \(x = 2,\,\,y =  - 6\)    

B. \(x = 4,\,\,y = 6\)       

C. \(x = 2,\,\,y = 5\)

D. \(x = 4,\,\,y =  - 6\)

Câu 16 .Cho \(C = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} - mx + m - 1}}{{{x^2} - 1}}\). Tìm tất cả các giá trị thực của \(m\) để \(C = 2\).

A. \(m = 1\) B. \(m = 2\)

C. \(m =  - 2\)       D. \(m =  - 1\)

II. PHẦN TỰ LUẬN

Câu 1 .Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({S_6} = 18\) và \({S_{10}} = 110\). Tính \({S_{16}}\).

Câu 2 .Tính \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + 2x}  + x} \right)\).

Câu 3. Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} + x - 2}}{{x - 1}}\,\,khi\,\,x \ne 1\\\,\,\,\,\,\,\,{a^2}\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\). Tìm tất cả các giá trị thực của tham số \(a\) để hàm số liên tục tại \(x = 1\).

Câu 4. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, cạnh \(SA\) vuông góc với mặt đáy, \(AB = a\), \(SA = a\sqrt 3 \), \(BC = a\sqrt 2 \).

          1) Chứng minh \(BC \bot \left( {SAB} \right)\).

          2) Gọi \(E\) là trung điểm của cạnh \(BC\). Chứng minh \(BD \bot SE\).

          3) Gọi \(\alpha \) là góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {SBD} \right)\). Tính \(\cos \alpha \).

Lời giải chi tiết

 

 

Câu 1 (VD)

Phương pháp:

- Chia tử cho mẫu.

- Tính giới hạn, lập hệ phương trình hai ẩn \(a,\,\,b\).

Cách giải:

Ta có:

\(\begin{array}{l}\,\,\,\,\,\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} + ax + b}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{{x\left( {x - 2} \right) + \left( {a + 2} \right)\left( {x - 2} \right) + 2a + b + 4}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \left( {x + a + 2 + \dfrac{{2a + b + 4}}{{x - 2}}} \right)\\ = 4 + a + \mathop {\lim }\limits_{x \to 2} \dfrac{{2a + b + 4}}{{x - 2}}\end{array}\)

Để \(\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} + ax + b}}{{x - 2}} = 6\) thì \(\left\{ \begin{array}{l}4 + a = 6\\2a + b + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 8\end{array} \right.\).

Vậy \(a + b = 2 + \left( { - 8} \right) =  - 6\).

Chọn D.

Câu 2 (TH)

Phương pháp:

- Xác định vectơ bằng vectơ \(\overrightarrow {EG} \) hoặc bằng vectơ \(\overrightarrow {AB} \).

- Sử dụng công thức: \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \angle \left( {\overrightarrow a ;\overrightarrow b } \right)\).

Cách giải:

 

Ta có: \(\overrightarrow {EG}  = \overrightarrow {AC} \), do đó

\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {EG}  = \overrightarrow {AB} .\overrightarrow {AC}  = AB.AC.\cos \angle BAC\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = a.a\sqrt 2 .\cos {45^0} = {a^2}\end{array}\)

Chọn B.

Câu 3 (TH)

Phương pháp:

Chứng minh hiệu \(H = {u_{n + 1}} - {u_n} = const\,\,\forall n\).

Cách giải:

Xét đáp án A ta có: \(\left( {{u_n}} \right) = {\left( {n + 1} \right)^2} - {n^2} = 2n + 1\).

\( \Rightarrow H = {u_{n + 1}} - {u_n}\\ = 2\left( {n + 1} \right) + 1 - 2n - 1 = 2\,\,\forall n\), do đó đây là CSC.

Xét đáp án B: \(H = {u_{n + 1}} - {u_n}\\ = 3\left( {n + 1} \right) - 1 - 3n + 1 = 3\,\,\forall n\), do đó đây là CSC.

Xét đáp án C: \(H = {u_{n + 1}} - {u_n} = 2018\), do đó đây là CSC.

Vậy đáp án D không là cấp số cộng.

Chọn D.

Câu 4 (TH)

Phương pháp:

- Sử dụng hằng đẳng thức.

- Rút gọn để khử dạng 0/0 và tính giới hạn.

Cách giải:

Ta có:

\(\begin{array}{l}\,\,\,\,\,\mathop {\lim }\limits_{x \to a} \dfrac{{{x^4} - {a^4}}}{{x - a}} \\= \mathop {\lim }\limits_{x \to a} \dfrac{{\left( {x - a} \right)\left( {x + a} \right)\left( {{x^2} + {a^2}} \right)}}{{x - a}}\\ = \mathop {\lim }\limits_{x \to a} \left( {x + a} \right)\left( {{x^2} + {a^2}} \right) = 2a.2{a^2} \\= 4{a^3}\end{array}\)

Chọn C.

Câu 5 (NB)

Phương pháp:

Sử dụng định lí: Nếu \(\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap \,c \subset \left( P \right)\end{array} \right.\) thì \(a \bot \left( P \right)\).

Cách giải:

Dễ thấy đáp án D sai do thiếu điều kiện \(b,\,\,c\) phải cắt nhau.

Chọn D.

Câu 6 (NB)

Phương pháp:

Chia cả tử và mẫu cho \({n^3}\).

Cách giải:

\(\lim \dfrac{{\left( {2{n^2} + 1} \right)n}}{{3 + n - 3{n^3}}} \\= \lim \dfrac{{2 + \dfrac{1}{{{n^2}}}}}{{\dfrac{3}{{{n^3}}} + \dfrac{1}{{{n^2}}} - 3}} =  - \dfrac{2}{3}\).

Chọn C.

Câu 7 (VD)

Phương pháp:

- Chọn \(SC \subset \left( {SAC} \right)\), xác định \(d = \left( {GMN} \right) \cap \left( {SAC} \right)\).

- Xác định \(H = SC \cap \left( {GMN} \right) = SC \cap d\).

- Sử dụng định lí Menelaus trong tam giác để tính tỉ số.

Cách giải:

 

Gọi \(O = AC \cap BD \Rightarrow O\) là trung điểm của \(AC,\,\,BD\).

\( \Rightarrow SO\) là đường trung tuyến của \(\Delta SBD \Rightarrow G \in SO \Rightarrow G \in \left( {SAC} \right)\).

Chọn \(SC \subset \left( {SAC} \right)\).

Xét \(\left( {GMN} \right)\) và \(\left( {SAC} \right)\) có \(G\) chung.

Trong \(\left( {ABCD} \right)\) gọi \(E = MN \cap AC\) ta có: \(\left\{ \begin{array}{l}E \in MN \subset \left( {GMN} \right)\\E \in AC \subset \left( {SAC} \right)\end{array} \right.\) \( \Rightarrow E \in \left( {GMN} \right) \cap \left( {SAC} \right)\).

\( \Rightarrow \left( {GMN} \right) \cap \left( {SAC} \right) = GE\).

Trong \(\left( {SAC} \right)\) gọi \(H = GE \cap SC\) ta có \(\left\{ \begin{array}{l}H \in SC\\H \in GE \subset \left( {GMN} \right)\end{array} \right. \Rightarrow H = SC \cap \left( {GMN} \right)\).

Ta có \(MN\) là đường trung bình của \(\Delta ABD \Rightarrow MN//BD\).

Xét tam giác \(ABC\) có: \(M\) là trung điểm của \(AB,\,\,ME//BO\) nên \(E\) là trung điểm của \(AO\) (định lí đường trung bình của tam giác) \( \Rightarrow \dfrac{{EO}}{{EC}} = \dfrac{1}{3}\).

Áp dụng định lí Menelaus trong tam giác \(SOC\), cát tuyến \(EGH\) ta có \(\dfrac{{GS}}{{GO}}.\dfrac{{EO}}{{EC}}.\dfrac{{HC}}{{HS}} = 1\)

\( \Rightarrow 2.\dfrac{1}{3}.\dfrac{{HC}}{{HS}} = 1 \Rightarrow \dfrac{{HC}}{{HS}} = \dfrac{3}{2}\) \( \Rightarrow \dfrac{{SH}}{{SC}} = \dfrac{2}{5}\).

Chọn B.

Câu 8 (TH)

Phương pháp:

Tính giới hạn từng đáp án.

- Đáp án A: chia cả tử và mẫu cho \({n^3}\).

- Đáp án B: Nhân liên hợp sau đó chia cả tử và mẫu cho \(n\).

- Đáp án C: Sử dụng công thức \(\lim {c^n} =  + \infty \,\,\forall c > 0\).

- Đáp án D: Nhân liên hợp sau đó sử dụng giới hạn \(\lim \dfrac{1}{{{n^\alpha }}} = 0\,\,\forall \alpha  > 0\).

Cách giải:

Đáp án A: ta có \(\lim {u_n} = \lim \dfrac{{2{n^3} - 11n + 1}}{{{n^2} - 2}}\)\( = \lim \dfrac{{2 - \dfrac{{11}}{{{n^2}}} + \dfrac{1}{{{n^3}}}}}{{\dfrac{1}{n} - \dfrac{2}{{{n^3}}}}} =  + \infty \).

Đáp án B: \(\lim {u_n} = \lim \left( {\sqrt {{n^2} + 2}  - n} \right)\)\( = \lim \dfrac{2}{{\sqrt {{n^2} + 2}  + n}} = 0\).

Đáp án C: \(\lim {u_n} = \lim \left( {{3^n} + {2^n}} \right) =  + \infty \).

Đáp án D: \(\lim {u_n} = \lim \dfrac{1}{{\sqrt {{n^2} - 2}  - \sqrt {{n^2} + 4} }}\) \( = \lim \dfrac{{\sqrt {{n^2} - 2}  + \sqrt {{n^2} + 4} }}{2} =  + \infty \).

Chọn B.

Câu 9 (NB)

Phương pháp:

Giới hạn của hàm đa thức phụ thuộc vào dấu của hệ số của bậc cao nhất.

Cách giải:

Dễ thấy \(\mathop {\lim }\limits_{x \to  + \infty } \left( {4{x^2} - 7{x^3} + 2} \right) =  - \infty \) nên đáp án A sai.

Chọn A.

Câu 10 (TH)

Phương pháp:

- Tính \(q = \dfrac{{{u_2}}}{{{u_1}}}\).

- Tính \({u_5} = {u_1} + 4d\).

Cách giải:

Gọi \(d\) là công sai của CSC ta có \(d = {u_2} - {u_1} =  - 6 - 3 =  - 9\).

Vậy \({u_5} = {u_1} + 4d = 3 + 4.\left( { - 9} \right) =  - 33\).

Chọn A.

Câu 11 (TH)

Phương pháp:

- Sử dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\), công bội \(q\) là \(S = \dfrac{{{u_1}}}{{1 - q}}\).

- Đồng nhất hệ số tìm \(m,\,\,n\).

Cách giải:

Ta có: \(1;\,\, - \dfrac{1}{2};\,\,\dfrac{1}{4};\,\, - \dfrac{1}{8};\,...;{\left( { - \dfrac{1}{2}} \right)^n},\,\,...\) là cấp số nhân lùi vô hạn với \({u_1} = 1,\,\,q =  - \dfrac{1}{2}\) nên

\(1 + \left( { - \dfrac{1}{2}} \right) + \dfrac{1}{4} + \left( { - \dfrac{1}{8}} \right) + ...\)\( + {\left( { - \dfrac{1}{2}} \right)^n} = \dfrac{1}{{1 - \dfrac{1}{2}}} = 2\).

\( \Rightarrow m = 2,\,\,n = 1\). Vậy \(m + 2n = 2.2 + 1 = 5\).

Chọn A.

Câu 12 (TH)

Phương pháp:

Chia cả tử và mẫu cho \({2019^n}\).

Cách giải:

Ta có:

\(\begin{array}{l}\,\,\,\,\lim \dfrac{{{{2018}^n} + {2^{2018}}}}{{{{2019}^n}}}\\ = \lim \left[ {{{\left( {\dfrac{{2018}}{{2019}}} \right)}^n} + \dfrac{{{2^{2018}}}}{{{{2019}^n}}}} \right]\\ = 0 + 0 = 0\end{array}\)

Chọn A.

Câu 13 (TH)

Phương pháp:

- Gọi \(M\) là trung điểm của \(CD\).

- Chứng minh \(CD\) vuông góc với mặt phẳng chứa \(AB\).

- Sử dụng các định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\), \(\left\{ \begin{array}{l}d \bot \left( P \right)\\\forall a \subset \left( P \right)\end{array} \right. \Rightarrow d \bot a\).

Cách giải:

 

Gọi \(M\) là trung điểm của \(CD\).

Vì tứ diện \(ABCD\) đều nên các tam giác \(ACD,\,\,BCD\) là các tam giác đều.

\( \Rightarrow \left\{ \begin{array}{l}AM \bot CD\\BM \bot CD\end{array} \right. \Rightarrow CD \bot \left( {ABM} \right)\). Mà \(AB \subset \left( {ABM} \right)\) nên \(AB \bot CD\).

Vậy \(\angle \left( {AB;CD} \right) = {90^0}\).

Chọn C.

Câu 14 (TH)

Phương pháp:

Sử dụng phương pháp nhân liên hợp.

Cách giải:

\(\begin{array}{l}\lim \left( {\sqrt {{n^2} + n}  - n} \right) \\= \lim \dfrac{{{n^2} + n - {n^2}}}{{\sqrt {{n^2} + n}  + n}}\\ = \lim \dfrac{n}{{\sqrt {{n^2} + n}  + n}}\\ = \lim \dfrac{1}{{\sqrt {1 + \dfrac{1}{n}}  + 1}} = \dfrac{1}{2}\end{array}\)

Chọn B.

Câu 15 (TH)

Phương pháp:

Sử dụng tính chất cấp số cộng: Nếu ba số \(a,\,\,b,\,\,c\) theo thứ tự lập thành cấp số cộng thì \(a + c = 2b\).

Cách giải:

Vì \(6,\,\,x,\,\, - 2,\,\,y\) theo thứ tự lập thành cấp số cộng nên ta có: \(\left\{ \begin{array}{l}6 + \left( { - 2} \right) = 2x\\x + y = 2.\left( { - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 4\\x + y =  - 4\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y =  - 6\end{array} \right.\).

Chọn A.

Câu 16 (TH)

Phương pháp:

- Phân tích thành nhân tử, rút gọn để khử dạng 0/0.

- Tính giới hạn, giải phương trình \(C = 2\) để tìm \(m\).

Cách giải:

Ta có:

\(\begin{array}{l}C = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} - mx + m - 1}}{{{x^2} - 1}}\\C = \mathop {\lim }\limits_{x \to 1} \left[ {1 - \dfrac{{m\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}} \right]\\C = \mathop {\lim }\limits_{x \to 1} \left( {1 - \dfrac{m}{{x + 1}}} \right) = 1 - \dfrac{m}{2}\\ \Rightarrow 1 - \dfrac{m}{2} = 2 \Leftrightarrow \dfrac{m}{2} =  - 1 \Leftrightarrow m =  - 2\end{array}\)

Chọn C.

II. PHẦN TỰ LUẬN

Câu 1 (TH)

Phương pháp:

Sử dụng công thức tính tổng \(n\) số hạng đầu tiên của cấp số cộng có số hạng đầu \({u_1}\), công sai \(d\) là \({S_n} = \dfrac{{\left( {2{u_1} + \left( {n - 1} \right)d} \right).n}}{2}\).

Cách giải:

Gọi \({u_1}\) là số hạng đầu và \(d\) là công sai của CSC.

Theo bài ra ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}{S_6} = 18\\{S_{10}} = 110\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{\left( {2{u_1} + 5d} \right).6}}{2} = 18\\\dfrac{{\left( {2{u_1} + 9d} \right).10}}{2} = 110\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2{u_1} + 5d = 6\\2{u_1} + 9d = 22\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} =  - 7\\d = 4\end{array} \right.\end{array}\)

Vậy \({S_{16}} = \dfrac{{\left( {2{u_1} + 15d} \right).16}}{2} \\= \dfrac{{\left( {2.\left( { - 7} \right) + 15.4} \right).16}}{2} = 368\).

Câu 2 (TH)

Phương pháp:

Sử dụng phương pháp nhân liên hợp.

Cách giải:

Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + 2x}  + x} \right) \\= \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{{x^2} + 2x - {x^2}}}{{\sqrt {{x^2} + 2x}  - x}}\\ = \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{2x}}{{\sqrt {{x^2} + 2x}  - x}}\\=\mathop {\lim }\limits_{x \to  - \infty } \dfrac{2}{{ - \sqrt {1 + \dfrac{2}{x}}  - 1}} =  - 1\end{array}\)

Câu 3 (TH)

Phương pháp:

Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).

Cách giải:

Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} + x - 2}}{{x - 1}} \\= \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x + 2} \right)\\ = 3\\f\left( 1 \right) = {a^2}\end{array}\)

Để hàm số liên tục tại \(x = 1\) thì \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right) \Leftrightarrow {a^2} = 3 \Leftrightarrow a =  \pm \sqrt 3 \).

Vậy \(a =  \pm \sqrt 3 \).

Câu 4 (VDC):

Phương pháp:

1) Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\).

2) Sử dụng định lí Ta-lét và định lí Pytago, tính độ dài các cạnh AI, BI.

Sử dụng định lí Pytago đảo chứng minh tam giác ABI vuông tại I.

Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\), \(\left\{ \begin{array}{l}d \bot \left( P \right)\\\forall a \subset \left( P \right)\end{array} \right. \Rightarrow d \bot a\).

3) Xác định hình chiếu vuông góc của điểm C lên (SBD), từ đó xác định góc giữa SC và (SBD).

Sử dụng định lí Pytago, định lí Ta-lét, tam giác đồng dạng tính độ dài đoạn thẳng CK.

Tính \(\sin \alpha \), từ đó tính \(\cos \alpha \).

Cách giải:

 

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, cạnh \(SA\) vuông góc với mặt đáy, \(AB = a\), \(SA = a\sqrt 3 \), \(BC = a\sqrt 2 \).

1) Chứng minh \(BC \bot \left( {SAB} \right)\).

Ta có: \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\).

2) Gọi \(E\) là trung điểm của cạnh \(BC\). Chứng minh \(BD \bot SE\).

Gọi \(I = AE \cap BD\).

Áp dụng định lí Ta-lét ta có:

\(BC//AD \Rightarrow \dfrac{{BI}}{{DI}} = \dfrac{{BE}}{{AD}} = \dfrac{1}{2}\), \(\dfrac{{AI}}{{EI}} = \dfrac{{AD}}{{BE}} = 2\).

\(\begin{array}{l} \Rightarrow BI = \dfrac{1}{3}BD = \dfrac{1}{3}\sqrt {A{B^2} + A{D^2}} \\ = \dfrac{{a\sqrt 3 }}{3}\\\,\,\,\,\,\,AI = \dfrac{2}{3}AE = \dfrac{2}{3}\sqrt {A{B^2} + B{E^2}} \\ = \dfrac{{a\sqrt 6 }}{3}\end{array}\)

Xét tam giác \(ABI\) có: \(A{I^2} + B{I^2} = {\left( {\dfrac{{a\sqrt 6 }}{3}} \right)^2} + {\left( {\dfrac{{a\sqrt 3 }}{3}} \right)^2}\\ = {a^2} = A{B^2}\).

\( \Rightarrow \Delta ABI\) vuông tại \(I\) \( \Rightarrow AI \bot BI\) hay \(AE \bot BD\).

Ta có: \(\left\{ \begin{array}{l}BD \bot AE\\BD \bot SA\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAE} \right)\).

Mà \(SE \subset \left( {SAE} \right) \Rightarrow BD \bot SE\,\,\left( {dpcm} \right)\).

3) Gọi \(\alpha \) là góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {SBD} \right)\). Tính \(\cos \alpha \).

Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AD,\,\,SD\) ta có \(\left\{ \begin{array}{l}CM//AE\\MN//SA\end{array} \right. \Rightarrow \left( {CMN} \right)//\left( {SAE} \right)\).

Mà \(\left( {SAE} \right) \bot BD\,\,\,\left( {cmt} \right) \Rightarrow \left( {CMN} \right) \bot BD\).

Gọi \(H = CM \cap BD\). Trong \(\left( {CMN} \right)\) kẻ \(CK \bot HN\,\,\left( {K \in HN} \right)\) ta có:

\(\left\{ \begin{array}{l}CK \bot HN\\CK \bot BD\end{array} \right. \Rightarrow CK \bot \left( {SBD} \right)\).

\( \Rightarrow SK\) là hình chiếu vuông góc của \(CK\) lên \(\left( {SBD} \right)\) \( \Rightarrow \angle \left( {SC;\left( {SBD} \right)} \right) = \angle \left( {SC;SK} \right) = \angle KSC\).

 

Dễ thấy \(\Delta MHN \sim \Delta KHC\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{KC}}{{MN}} = \dfrac{{HC}}{{HN}}\).

Ta có: \(MN = \dfrac{1}{2}SA = \dfrac{{a\sqrt 3 }}{2}\).

Áp dụng định lí Ta-lét ta có: \(\dfrac{{HC}}{{HM}} = \dfrac{{BC}}{{MD}} = 2 \Rightarrow HC = \dfrac{2}{3}MC = \dfrac{2}{3}AE = AI = \dfrac{{a\sqrt 6 }}{3}\).

\( \Rightarrow HM = \dfrac{1}{2}HC = \dfrac{{a\sqrt 6 }}{6}\). Áp dụng định lí Pytago ta có: \(HN = \sqrt {M{N^2} + H{M^2}}  = \dfrac{{a\sqrt {33} }}{6}\).

\( \Rightarrow KC = \dfrac{{MN.HC}}{{HN}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 6 }}{3}}}{{\dfrac{{a\sqrt {33} }}{6}}} = \dfrac{{a\sqrt {66} }}{{11}}\).

Ta lại có: \(AC = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 3  \Rightarrow SC = \sqrt {S{A^2} + A{C^2}}  = a\sqrt 6 \).

Vì \(CK \bot \left( {SBD} \right) \Rightarrow CK \bot SK \Rightarrow \Delta SCK\) vuông tại K.

Ta có: \(\sin \angle KSC = \dfrac{{KC}}{{SC}} = \dfrac{{a\sqrt {66} }}{{11}}:a\sqrt 6  = \dfrac{{\sqrt {11} }}{{11}}\).

Vậy \(\cos \alpha  = \sqrt {1 - \dfrac{1}{{11}}}  = \dfrac{{\sqrt {110} }}{{11}}\).

HocTot.Nam.Name.Vn