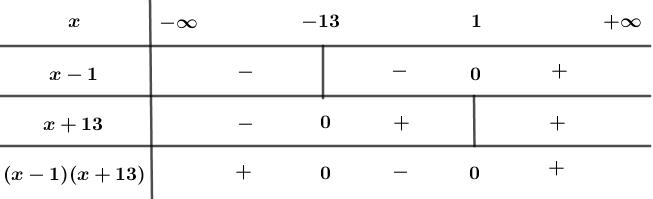
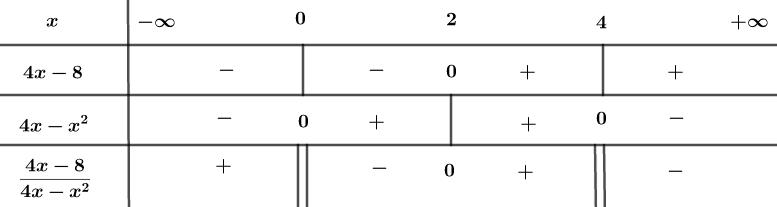
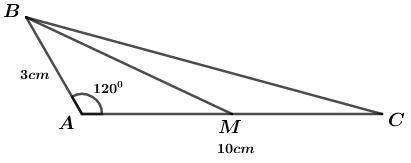
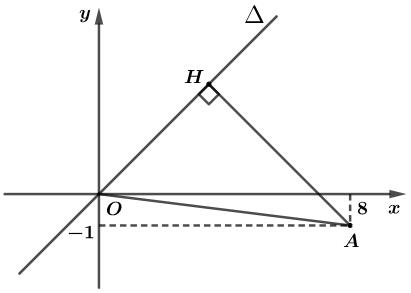
Đề kiểm tra giữa kì 2 Toán 10 - đề số 2 có lời giải chi tiết

Đề bài

Câu 1 (2,0 điểm):

1) Giải bất phương trình \(5{x^2} - {\left( {3 - 2x} \right)^2} \ge 4\).

2) Giải phương trình \(9 - \sqrt {3x + 1}  = x\).

Câu 2 (2,0 điểm):

1) Tìm tập xác định của hàm số \(f\left( x \right) = \sqrt {1 - \dfrac{{8 - {x^2}}}{{4x - {x^2}}}} \)

2) Giải bất phương trình \({x^2} - 2\left| {x - 1} \right| + 2 > 0\).

Câu 3 (2,0 điểm):

1) Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} - 2\left( {m - 1} \right)x - 4m < 0\) vô nghiệm.

2) Giải bất phương trình \(\sqrt {{x^2} + 3}  \ge 2x\).

Câu 4 (1,5 điểm): Cho tam giác \(ABC\) có \(AB = 3cm,\,\,AC = 10cm,\)\(\angle BAC = {120^0}\).

1) Tính diện tích tam giác \(ABC\).

2) Tính độ dài đường trung tuyến kẻ từ đỉnh \(B\) của tam giác \(ABC\).

Câu 5 (1,5 điểm): Trong mặt phẳng với hệ tọa độ \(Oxy\), cho điểm \(A\left( {8;\,\, - 1} \right)\) và đường thẳng \(d\) có phương trình \(2x - y - 7 = 0\).

1) Viết phương trình tham số của đường thẳng \(d\). Tìm điểm \(M\) thuộc \(d\) sao cho \(AM = 5\).

2) Trong các đường thẳng đi qua \(O\), hãy viết phương trình tổng quát của đường thẳng mà khoảng cách từ \(A\) đến đường thẳng đó là lớn nhất.

Câu 6 (1,0 điểm): Cho \(x \ge  - 1\). Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{{x + 1}}{{\sqrt {{x^2} + 1} }}\).

Lời giải chi tiết

Câu 1 (VD)

Phương pháp:

1) Đưa về bất phương trình tích sau đó lập bảng xét dấu.

2) Tìm ĐKXĐ của bất phương trình.

Áp dụng: \(\sqrt {f\left( x \right)}  = g\left( x \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\)

Cách giải:

1) Giải bất phương trình \(5{x^2} - {\left( {3 - 2x} \right)^2} \ge 4\).

\(\begin{array}{l}\,\,\,\,\,\,5{x^2} - {\left( {3 - 2x} \right)^2} \ge 4\\ \Leftrightarrow 5{x^2} - \left( {9 - 12x + 4{x^2}} \right) \ge 4\\ \Leftrightarrow 5{x^2} - 9 + 12x - 4{x^2} - 4 \ge 0\\ \Leftrightarrow {x^2} + 12x - 13 \ge 0\\ \Leftrightarrow {x^2} + 13x - x - 13 \ge 0\\ \Leftrightarrow \left( {{x^2} + 13x} \right) - \left( {x + 13} \right) \ge 0\\ \Leftrightarrow x\left( {x + 13} \right) - \left( {x + 13} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 13} \right) \ge 0\end{array}\)

Ta có bảng xét dấu của bất phương trình:

Từ bảng xét dấu, ta thấy để \(\left( {x - 1} \right)\left( {x + 13} \right) \ge 0\)thì \(x \in \left( { - \infty ;\,\, - 13} \right] \cup \left[ {1;\,\, + \infty } \right)\)

Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ;\,\, - 13} \right] \cup \left[ {1;\,\, + \infty } \right)\).

2) Giải phương trình \(9 - \sqrt {3x + 1}  = x\).

Điều kiện xác định : \(3x + 1 \ge 0\)\( \Leftrightarrow x \ge  - \dfrac{1}{3}\)

     \(9 - \sqrt {3x + 1}  = x\)\( \Leftrightarrow \sqrt {3x + 1}  = 9 - x\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}9 - x \ge 0\\3x + 1 = {\left( {9 - x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - x \ge 0\\{x^2} - 21x + 80 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 9\\\left( {x - 5} \right)\left( {x - 16} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 9\\\left[ \begin{array}{l}x - 5 = 0\\x - 16 = 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 9\\\left[ \begin{array}{l}x = 5\,\,\\x = 16\,\end{array} \right.\end{array} \right. \Leftrightarrow x = 5\end{array}\)

Vậy nghiệm của phương trình là \(x = 5\).

Câu 2 (VD)

Phương pháp:

1) \(f\left( x \right) = \dfrac{{A\left( x \right)}}{{B\left( x \right)}}\) xác định khi và chỉ khi \(B\left( x \right) \ne 0\); \(f\left( x \right) = \sqrt {P\left( x \right)} \) xác định  khi và chỉ khi \(P\left( x \right) \ge 0\)

2) Xét từng trường hợp: \(\left| {f\left( x \right)} \right| = f\left( x \right)\) nếu \(f\left( x \right) \ge 0\); \(\left| {f\left( x \right)} \right| =  - f\left( x \right)\) nếu \(f\left( x \right) < 0\).

Cách giải:

1) Tìm tập xác định của hàm số \(f\left( x \right) = \sqrt {1 - \dfrac{{8 - {x^2}}}{{4x - {x^2}}}} \).

Hàm số \(f\left( x \right) = \sqrt {1 - \dfrac{{8 - {x^2}}}{{4x - {x^2}}}} \) xác định khi và chỉ khi :

\(\left\{ \begin{array}{l}1 - \dfrac{{8 - {x^2}}}{{4x - {x^2}}} \ge 0\\4x - {x^2} \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{4x - {x^2}}}{{4x - {x^2}}} - \dfrac{{8 - {x^2}}}{{4x - {x^2}}} \ge 0\\x\left( {4 - x} \right) \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{4x - 8}}{{4x - {x^2}}} \ge 0\,\,\,\,\left( * \right)\\x \ne 0\,;x \ne 4\end{array} \right.\)

Ta có bảng xét dấu của bất phương trình \(\left( * \right)\):

Từ bảng xét dấu, ta thấy để \(\dfrac{{4x - 8}}{{4x - {x^2}}} \ge 0\,\)thì \(x \in \left( { - \infty ;\,\,0} \right) \cup \left[ {2;\,\,4} \right)\)

Vậy tập xác định của hàm số là: \(D = \left( { - \infty ;\,\,0} \right) \cup \left[ {2;\,\,4} \right)\)

2) Giải bất phương trình \({x^2} - 2\left| {x - 1} \right| + 2 > 0\).

Trường hợp 1: \(x - 1 \ge 0\)\( \Leftrightarrow x \ge 1\)

Bất phương trình trở thành:

\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} - 2\left( {x - 1} \right) + 2 > 0\\ \Leftrightarrow {x^2} - 2x + 4 > 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + 3 > 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + 3 > 0\,\,\,\forall \,x \in \mathbb{R}\end{array}\)

Vậy bất phương trình có nghiệm là \(x \ge 1\).

Trường hợp 2: \(x - 1 < 0\)\( \Leftrightarrow x < 1\)

Bất phương trình trở thành:

\(\begin{array}{l}{x^2} - 2\left( { - x + 1} \right) + 2 > 0\\ \Leftrightarrow {x^2} + 2x - 2 + 2 > 0\\ \Leftrightarrow {x^2} + 2x > 0\\ \Leftrightarrow x\left( {x + 2} \right) > 0\\ \Leftrightarrow \left[ \begin{array}{l}x > 0\\x <  - 2\end{array} \right.\end{array}\)

Kết hợp với điều kiện \(x < 1\) ta được nghiệm thỏa mãn hệ phương trình sau :

\(\left\{ \begin{array}{l}x < 1\\\left[ \begin{array}{l}x > 0\\x <  - 2\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 1\\x > 0\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\x <  - 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}0 < x < 1\\x <  - 2\end{array} \right.\)

Kết hợp trường hợp 1 và trường hợp 2 , ta được nghiệm của bất phương trình là \(\left[ \begin{array}{l}x > 0\\x <  - 2\end{array} \right.\)

Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ;\,\, - 2} \right) \cup \left( {0;\,\, + \infty } \right)\).

Câu 3 (VD)

Phương pháp:

1) \(f\left( x \right) < 0\) vô nghiệm \( \Leftrightarrow \)\(f\left( x \right) \ge 0\) có nghiệm với mọi \(x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\)

2) Áp dụng \(\sqrt {f\left( x \right)}  \ge g\left( x \right)\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) \le 0\end{array} \right.\\\left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) \ge {g^2}\left( x \right)\end{array} \right.\end{array} \right.\)

Cách giải:

1) Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} - 2\left( {m - 1} \right)x - 4m < 0\) vô nghiệm.

Bất phương trình \({x^2} - 2\left( {m - 1} \right)x - 4m < 0\) vô nghiệm

\( \Leftrightarrow \) \({x^2} - 2\left( {m - 1} \right)x - 4m \ge 0\) có nghiệm với mọi \(x \in \mathbb{R}\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\,\,\,\left( {tm} \right)\\4{\left( {m - 1} \right)^2} - 4.1.\left( { - 4m} \right) \le 0\end{array} \right.\\ \Leftrightarrow 4{\left( {m - 1} \right)^2} - 4.1.\left( { - 4m} \right) \le 0\\ \Leftrightarrow 4\left( {{m^2} - 2m + 1} \right) + 16m \le 0\\ \Leftrightarrow 4{m^2} - 8m + 4 + 16m \le 0\\ \Leftrightarrow 4{m^2} + 8m + 4 \le 0\\ \Leftrightarrow 4{\left( {m + 1} \right)^2} \le 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} \le 0\end{array}\)

Mà \({\left( {m + 1} \right)^2} \ge 0\) với mọi \(m\) suy ra \({\left( {m + 1} \right)^2} = 0\)\( \Leftrightarrow \)\(m + 1 = 0 \Leftrightarrow m =  - 1\).

Vậy với \(m =  - 1\) thì bất phương trình \({x^2} - 2\left( {m - 1} \right)x - 4m < 0\) vô nghiệm.

2) Giải bất phương trình \(\sqrt {{x^2} + 3}  \ge 2x\).

\(\sqrt {{x^2} + 3}  \ge 2x\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2x \le 0\\{x^2} + 3 \ge 0\end{array} \right.\\\left\{ \begin{array}{l}2x \ge 0\\{x^2} + 3 \ge 4{x^2}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \le 0\\{x^2} + 3 \ge 0,\,\,\forall x \in \mathbb{R}\end{array} \right.\\\left\{ \begin{array}{l}x \ge 0\\{x^2} \le 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x \le 0\\\left\{ \begin{array}{l}x \ge 0\\ - 1 \le x \le 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \le 0\\0 \le x \le 1\end{array} \right. \Leftrightarrow x \le 1\end{array}\)

Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ;\,\,1} \right]\).

Câu 4 (VD)

Phương pháp:

1) Áp dụng công thức hàm số sin trong tính diện tích tam giác:

 \(S = \dfrac{1}{2}ab\sin C\)\( = \dfrac{1}{2}ac\sin B\)\( = \dfrac{1}{2}bc\sin A\)

2) Tính \(MA\) và \(MB\). Sau đó, áp dụng định lý côsin trong tam giác: \({a^2} = {b^2} + {c^2} - 2bc\cos A\).

Cách giải:

1) Tính diện tích tam giác \(ABC\).

\(\begin{array}{l}{S_{\Delta ABC}} = \dfrac{1}{2} \cdot AB \cdot AC \cdot \sin \angle BAC\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2} \cdot 3 \cdot 10 \cdot \sin {120^0} = \dfrac{{15\sqrt 3 }}{2}\left( {c{m^2}} \right)\end{array}\)

2) Tính độ dài đường trung tuyến kẻ từ đỉnh \(B\) của tam giác \(ABC\).

Gọi \(BM\) là đường trung tuyến kẻ từ đỉnh \(B\) của tam giác \(ABC\).

\( \Rightarrow M\) là trung điểm của \(AC\)

\( \Rightarrow AM = MC = \dfrac{{AC}}{2} = \dfrac{{10}}{2} = 5\left( {cm} \right)\)

Áp dụng định lý côsin trong tam giác \(ABM\) ta có:

\(\begin{array}{l}B{M^2} = A{B^2} + A{M^2} - 2.AB.AM.\cos \angle BAC\\\,\,\,\,\,\,\,\,\,\,\,\,\, = {3^2} + {5^2} - 2.3.5.\cos {120^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 49\end{array}\)

\( \Rightarrow BM = 7\left( {cm} \right)\)

Vậy độ dài đường trung tuyến kẻ từ đỉnh \(B\) của tam giác \(ABC\) là \(7\left( {cm} \right)\).

Câu 5 (VD)

Phương pháp:

1) Phương trình tham số của đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};\,\,{y_0}} \right)\) nhận \(\vec u = \left( {a;\,\,b} \right)\) là VTCP :

\(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + at\end{array} \right.\left( {t \in \mathbb{R}} \right)\)

2) Vẽ đồ thị hàm số; Áp dụng: Trong một tam giác vuông, cạnh huyền là cạnh lớn nhất.

Cách giải:

1) Viết phương trình tham số của đường thẳng \(d\). Tìm điểm \(M\) thuộc \(d\) sao cho \(AM = 5\).

*) Viết phương trình tham số của đường thẳng \(d\).  

\(d:\,\,2x - y - 7 = 0\)

Phương trình tham số của đường thẳng \(d\): \(\left\{ \begin{array}{l}x = t\\y =  - 7 + 2t\end{array} \right.\,\,\,\,\left( {t \in \mathbb{R}} \right)\)

Vì điểm \(M \in d\)\( \Rightarrow \)\(M\)có tọa độ là : \(M\left( {a;\,\,2a - 7} \right) \in d\)

 Có : \(A\left( {8;\,\, - 1} \right)\)\(,M\left( {a;\,\,2a - 7} \right)\).

\( \Rightarrow \overrightarrow {AM}  = \left( {a - 8;\,\,2a - 6} \right)\)

\(\begin{array}{l}AM = 5 \Leftrightarrow \sqrt {{{\left( {a - 8} \right)}^2} + {{\left( {2a - 6} \right)}^2}}  = 5\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {\left( {a - 8} \right)^2} + {\left( {2a - 6} \right)^2} = 25\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {a^2} - 16a + 64 + 4{a^2} - 24a + 36 - 25 = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 5{a^2} - 40a + 75 = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left( {a - 5} \right)\left( {5a - 15} \right) = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}a - 5 = 0\\5a - 15 = 0\end{array} \right.\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}a = 5\\a = 3\end{array} \right.\end{array}\)

+) Với \(a = 5 \Rightarrow M\left( {5;\,\,3} \right)\)

+) Với \(a = 3 \Rightarrow M\left( {3;\,\, - 1} \right)\)

Vậy \(M\left( {5;\,\,3} \right)\) hoặc \(M\left( {3;\,\, - 1} \right)\)thỏa mãn \(AM = 5\).

2) Trong các đường thẳng đi qua \(O\), hãy viết phương trình tổng quát của đường thẳng mà khoảng cách từ \(A\) đến đường thẳng đó là lớn nhất.

Kẻ \(AH \bot \Delta \) tại \(H\), khi đó \(AH\) là khoảng cách từ \(A\) đến đường thẳng \(\Delta \).

\(\Delta OHA\) vuông tại \(H\) nên \(AH \le OA\)(quan hệ giữa đường vuông góc và đường xiên trong tam giác vuông)

Dấu “\( = \)” xảy ra khi và chỉ khi \(H \equiv O\).

Do đó, \(AH\) đạt giá trị lớn nhất khi và chỉ khi \(H \equiv O\)\( \Leftrightarrow OA \bot \Delta \)

\( \Rightarrow {\vec n_\Delta } = {\vec u_{OA}} = \left( {8;\,\, - 1} \right)\)

\( \Rightarrow \) Phương trình tổng quát của đường thẳng \(\Delta \) đi qua \(O\left( {0;\,\,0} \right)\) là: \(8x - y = 0\)

Câu 6 (VD)

Phương pháp:

+ Biến đổi đề chứng minh \(y \ge 0\)

+ Tìm \(Max\): Áp dụng bất đẳng thức \({\left( {x + y} \right)^2} \le 2\left( {{x^2} + {y^2}} \right)\) hoặc bình phương hai vế.

Cách giải:

*) Tìm \(Min\,y\)

\(x \ge  - 1\) \( \Rightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\\sqrt {{x^2} + 1}  > 0\end{array} \right.\)\( \Rightarrow \dfrac{{x + 1}}{{\sqrt {{x^2} + 1} }} \ge 0\)\( \Rightarrow y \ge 0\)

Dấu xảy ra khi và chỉ khi \(x + 1 = 0 \Leftrightarrow x =  - 1\)

Vậy \(Min\,y = 0\)\( \Leftrightarrow x =  - 1\).

*) Tìm \(Max\,y\)

Với mọi \(x,\,y \in \mathbb{R}\) ta có:

\(\begin{array}{l}{\left( {x - y} \right)^2} \ge 0\\ \Leftrightarrow 2xy \le {x^2} + {y^2}\\ \Leftrightarrow 2xy + {x^2} + {y^2} \le {x^2} + {y^2} + {x^2} + {y^2}\\ \Leftrightarrow {x^2} + {y^2} + 2xy \le 2\left( {{x^2} + {y^2}} \right)\\ \Leftrightarrow {\left( {x + y} \right)^2} \le 2\left( {{x^2} + {y^2}} \right)\end{array}\)

Ta có:

\(\begin{array}{l}{\left( {x + 1} \right)^2} \le 2\left( {{x^2} + 1} \right)\\ \Leftrightarrow \dfrac{{{{\left( {x + 1} \right)}^2}}}{{{x^2} + 1}} \le 2\\ \Leftrightarrow \dfrac{{x + 1}}{{\sqrt {{x^2} + 1} }} \le \sqrt 2 \\ \Leftrightarrow y \le \sqrt 2 \end{array}\)

Dấuxảy ra khi và chỉ khi \(x = 1\)

Vậy \(Max\,y = \sqrt 2  \Leftrightarrow x = 1\).

HocTot.Nam.Name.Vn