Đề kiểm tra giữa kì 1 Toán 11 - Đề số 1 có lời giải chi tiết

Đề bài

PHẦN 1: TRẮC NGHIỆM (3 điểm)

Câu 1: Lớp có 50 học sinh trong đó có 20 học sinh nữ. Chọn 3 bạn tham gia đội văn nghệ. Số cách chọn sao cho có ít nhất 1 bạn nam là:

A. \(C_{30}^2.C_{20}^1\)            B. \(C_{50}^3 - C_{20}^3\)                                        

C. \(C_{50}^3 - C_{30}^3\)          D. \(C_{50}^3.C_{30}^3\)

Câu 2: Giá trị nhỏ nhất của hàm số \(y = 3\sin 2x - 2\) bằng:

A. \(4\)                                    B. \(1\)                               

C. \(5\)                                    D. \( - 5\)

Câu 3: Trong mặt phẳng, biết \({V_{\left( {O;k} \right)}}\left( M \right) = M'\). Chọn kết luận đúng.

A. \(\overrightarrow {OM}  = k\overrightarrow {OM'} \)        B. \(\overrightarrow {OM'}  = k\overrightarrow {OM} \)

C. \(\overrightarrow {OM'}  =  - k\overrightarrow {OM} \)     D. \(\overrightarrow {OM'}  = \left| k \right|\overrightarrow {OM} \)

Câu 4: Tập nghiệm của phương trình \(\cos x =  - \dfrac{{\sqrt 3 }}{2}\) là:

A. \(x =  \pm \dfrac{{5\pi }}{6} + k2\pi ,\,\,k \in \mathbb{Z}\)    

B. \(x =  \pm \dfrac{{2\pi }}{3} + k2\pi ,\,\,k \in \mathbb{Z}\)                         

C. \(x =  \pm \dfrac{\pi }{3} + k2\pi ,\,\,k \in \mathbb{Z}\) 

D. \(x =  \pm \dfrac{\pi }{6} + k\pi ,\,\,k \in \mathbb{Z}\)

Câu 5: Trong mặt phẳng tọa độ, cho \(M\left( { - 1;2} \right)\), \(k =  - \dfrac{1}{2}\), \({V_{\left( {O;k} \right)}}\left( M \right) = M'\), \(O\) là gốc tọa độ. Khi đó \(M'\) có tọa độ là:

A. \(M'\left( { - \dfrac{1}{2};1} \right)\)                           B. \(M'\left( {1; - \dfrac{1}{2}} \right)\)    C. \(M'\left( {\dfrac{1}{2}; - 1} \right)\)                                D. \(M'\left( { - 1;\dfrac{1}{2}} \right)\)

Câu 6: Tập xác định của hàm số \(y = \tan \left( {x - \dfrac{\pi }{3}} \right)\) là:

A. \(D = \mathbb{R}\backslash \left\{ { \pm \dfrac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)   

B. \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)

C. \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)             

D. \(D = \mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{6} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Câu 7: Nghiệm của phương trình \({\cos ^2}x - \cos x = 0\) thỏa mãn điều kiện \( - \pi  < x < 0\) là:

A. \(x = \dfrac{\pi }{6}\)         B. \(x = \dfrac{\pi }{4}\)    

C. \(x =  - \dfrac{\pi }{2}\)      D. \(x = \dfrac{\pi }{2}\)

Câu 8: Tập nghiệm của phương trình \(\sqrt 3 \sin x + \cos x = 0\) là:

A. \(x =  - \dfrac{\pi }{6} + k\pi ,\,\,k \in \mathbb{Z}\)     B. \(x =  - \dfrac{\pi }{3} + k2\pi ,\,\,k \in \mathbb{Z}\)   

C. \(x =  - \dfrac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\)     D. \(x = \dfrac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\)

Câu 9: Cho hình chóp \(S.ABCD\) có \(AC \cap BD = M\) và \(AB \cap CD = N\). Giao tuyến của mặt phẳng \(\left( {SAC} \right)\) và mặt phẳng \(\left( {SBD} \right)\) là đường thẳng

A. \(SM\)       B. \(SA\)      C. \(MN\)      D. \(SN\)

Câu 10: Trong mặt phẳng tọa độ, cho \(M\left( {1; - 2} \right)\), phép tịnh tiến theo vectơ \(\overrightarrow v \left( { - 3; - 3} \right)\) biến điểm \(M\) thành điểm \(M'\). Tọa độ điểm \(M'\) là:

A. \(M'\left( {2; - 5} \right)\)           B. \(M'\left( {4; - 1} \right)\)                               

C. \(M'\left( {2;5} \right)\)             D. \(M'\left( { - 2; - 5} \right)\)

Câu 11: Trên giá sách có 7 quyển sách Toán khác nhau, 5 quyển Vật lí khác nhau, 8 quyển sách Hóa học khác nhau. Số cách chọn 1 quyển sách để đọc là:

A. \(15\)           B. \(13\)           C. \(20\)           D. \(280\)

Câu 12: Cho 5 chữ số 1, 2, 3, 5, 6. Lập các số tự nhiên gồm 3 chữ số đôi một khác nhau từ 5 chữ số đã cho. Tổng tất cả các số lập được bằng:

A. \(22644\)     B. \(24642\)     C. \(26442\)     D. \(44622\)

II. PHẦN TỰ LUẬN (7 điểm)

Câu 1 (2,0 điểm): Giải các phương trình sau:

a) \(2\sin \left( {x - \dfrac{\pi }{6}} \right) - \sqrt 3  = 0\)                                                  

b) \(\sin x - \sqrt 3 \cos x =  - \sqrt 2 \)

Câu 2 (2,0 điểm):

a) Cho tập hợp \(A = \left\{ {1;2;3;4;5;6;7} \right\}\). Từ A có thể lập đươc bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau?

b) Lớp 11A có 15 học sinh nữ, 20 học sinh nam. Có bao nhiêu cách chọn 5 học sinh tham gia văn nghệ trong đó có ít nhất 3 học sinh nữ?

Câu 3 (3 điểm):

1. Trong mặt phẳng \(Oxy\) , cho vectơ \(\overrightarrow v \left( {2; - 1} \right)\) và đường thẳng \(x + y - 3 = 0\). Viết phương trình đường thẳng \(d'\) là ảnh của đường thẳng \(d\) qua phép tịnh tiến theo \(\overrightarrow v \).

2. Cho tứ diện \(ABCD\), gọi \(G\) là trọng tâm tam giác \(BCD\), \(M\) là trung điểm của \(CD\), \(I\) là điểm trên đoạn thẳng \(AG\).

a) Xác định giao tuyến của mặt phẳng \(\left( {ABG} \right)\) và mặt phẳng \(\left( {ACD} \right)\).

b) Xác định giao điểm \(J\) của \(BI\) với mặt phẳng \(\left( {ACD} \right)\). Tính tỉ số giữa \(AI\) và \(AG\) để diện tích tam giác \(ACD\) bằng 2 lần diện tích tam giác \(JCD\).

 

Lời giải chi tiết

PHẦN 1: TRẮC NGHIỆM (3 điểm)

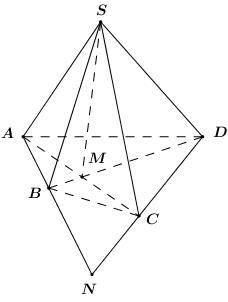
Câu 1:

Phương pháp:

Sử dụng phần bù.

Cách giải:

Số cách chọn 3 bạn bất kì là: \(C_{50}^3\) cách.

Số cách chọn 3 bạn nữ là; \(C_{20}^3\) cách.

Vậy số cách chọn 3 bạn trong đó có ít nhất 1 bạn nam là: \(C_{50}^3 - C_{20}^3\) cách.

Chọn B.

Câu 2:

Phương pháp:

Sử dụng tính chất: \( - 1 \le \sin \alpha  \le 1\,\,\forall \alpha \).

Cách giải:

Ta có:

\(\begin{array}{l}\,\,\,\,\,\, - 1 \le \sin 2x \le 1\\ \Leftrightarrow  - 3 \le 3\sin 2x \le 3\\ \Leftrightarrow  - 5 \le 3\sin 2x - 2 \le 1\\ \Leftrightarrow  - 5 \le y \le 1\end{array}\)

Vậy GTNN của hàm số bằng \( - 5\).

Chọn D.

Câu 3:

Phương pháp:

Sử dụng định nghĩa phép vị tự: \({V_{\left( {O;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {OM'}  = k\overrightarrow {OM} .\)

Cách giải:

Ta có: \({V_{\left( {O;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {OM'}  = k\overrightarrow {OM} .\)

Chọn B.

Câu 4:

Phương pháp:

Giải phương trình lượng giác cơ bản: \(\cos x = \cos \alpha  \Leftrightarrow x =  \pm \alpha  + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

Cách giải:

Ta có: \(\cos x =  - \dfrac{{\sqrt 3 }}{2} = \cos \dfrac{{5\pi }}{6} \Leftrightarrow x =  \pm \dfrac{{5\pi }}{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

Chọn A.

Câu 5:

Phương pháp:

Sử dụng định nghĩa phép vị tự: \({V_{\left( {O;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {OM'}  = k\overrightarrow {OM} .\)

Cách giải:

Gọi \(M'\left( {x';y'} \right) = {V_{\left( {O; - \dfrac{1}{2}} \right)}}\left( M \right)\) ta có:

\(\begin{array}{l}\overrightarrow {OM'}  =  - \dfrac{1}{2}\overrightarrow {OM} \\ \Leftrightarrow \left\{ \begin{array}{l}x' - {x_O} =  - \dfrac{1}{2}\left( {{x_M} - {x_O}} \right)\\y' - {y_O} =  - \dfrac{1}{2}\left( {{y_M} - {y_O}} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x' =  - \dfrac{1}{2}.\left( { - 1} \right)\\y' =  - \dfrac{1}{2}.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = \dfrac{1}{2}\\y' =  - 1\end{array} \right.\end{array}\)

Vậy \(M'\left( {\dfrac{1}{2}; - 1} \right)\).

Chọn C.

Câu 6:

Phương pháp:

Hàm số \(y = \tan \alpha \) xác định \( \Leftrightarrow \alpha  \ne \dfrac{\pi }{2} + k\pi \).

Cách giải:

Hàm số \(y = \tan \left( {x - \dfrac{\pi }{3}} \right)\) xác định \( \Leftrightarrow x - \dfrac{\pi }{3} \ne \dfrac{\pi }{2} + k\pi  \Leftrightarrow x \ne \dfrac{{5\pi }}{6} + k\pi \).

Vậy TXĐ của hàm số là \(D = \mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{6} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).

Chọn C.

Câu 7:

Phương pháp:

- Đưa phương trình về dạng phương trình tích.

- Giải phương trình lượng giác cơ bản.

- Giải bất phương trình \( - \pi  < x < 0\), tìm nghiệm \(x\) thỏa mãn.

Cách giải:

Ta có: \({\cos ^2}x - \cos x = 0 \Leftrightarrow \cos x\left( {\cos x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\\cos x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = \pi  + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

+ Xét họ nghiệm \(x = \dfrac{\pi }{2} + k\pi \).

Cho \( - \pi  < x < 0 \Leftrightarrow  - \pi  < \dfrac{\pi }{2} + k\pi  < 0 \Leftrightarrow  - \dfrac{3}{2} < k <  - \dfrac{1}{2}\).

Mà \(k \in \mathbb{Z} \Rightarrow k =  - 1 \Rightarrow x =  - \dfrac{\pi }{2}\).

+ Xét họ nghiệm \(x = \pi  + k2\pi \).

Cho \( - \pi  < \pi  + k2\pi  < 0 \Leftrightarrow  - 1 < k <  - \dfrac{1}{2}\).

Mà \(k \in \mathbb{Z} \Rightarrow k \in \emptyset \).

Vậy phương trình đã cho có duy nhất 1 nghiệm thỏa mãn là \(x =  - \dfrac{\pi }{2}\).

Chọn C.

Câu 8:

Phương pháp:

- Chuyến vế, đưa về phương trình hàm tan.

- Giải phương trình lượng giác cơ bản: \(\tan x = \tan \alpha  \Leftrightarrow x = \alpha  + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

Cách giải:

Ta có:

\(\begin{array}{l}\sqrt 3 \sin x + \cos x = 0 \Leftrightarrow \sqrt 3 \sin x =  - \cos x\\ \Leftrightarrow \tan x =  - \dfrac{1}{{\sqrt 3 }} \Leftrightarrow x =  - \dfrac{\pi }{6} + k\pi \,\,\left( {k \in } \right)\end{array}\).

Chọn A.

Câu 9:

Phương pháp:

Xác định hai điểm chung của hai mặt phẳng, từ đó xác định giao tuyến.

Cách giải:

 

Xét \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) có:

+ \(S\) là điểm chung thứ nhất.

+ Trong \(\left( {ABCD} \right)\) ta có \(M = AC \cap BD \Rightarrow \left\{ \begin{array}{l}M \in AC \subset \left( {SAC} \right)\\M \in BD \subset \left( {SBD} \right)\end{array} \right.\) \( \Rightarrow M \in \left( {SAC} \right) \cap \left( {SBD} \right)\).

Vậy \(\left( {SAC} \right) \cap \left( {SBD} \right) = SM\).

Chọn A.

Câu 10:

Phương pháp:

Sử dụng định nghĩa phép tịnh tiến: \({T_{\overrightarrow u }}\left( M \right) = M' \Rightarrow \overrightarrow {MM'}  = \overrightarrow u \).

Cách giải:

Ta có: \({T_{\overrightarrow u }}\left( M \right) = M' \Rightarrow \overrightarrow {MM'}  = \overrightarrow u \)

 \( \Rightarrow \left\{ \begin{array}{l}{x_{M'}} = 1 + \left( { - 3} \right) =  - 2\\{y_{M'}} =  - 2 + \left( { - 3} \right) =  - 5\end{array} \right.\).

Vậy \(M'\left( { - 2; - 5} \right)\).

Chọn D.

Câu 11:

Phương pháp:

- Tính số cách chọn 1 quyển sách Toán, 1 quyển sách Vật lí, 1 quyển sách Hóa.

- Sử dụng quy tắc cộng.

Cách giải:

Số cách chọn 1 quyển sách Toán là 7 cách.

Số cách chọn 1 quyển sách Vật lí là 5 cách.

Số cách chọn 1 quyển sách Hóa là 8 cách.

Áp dụng quy tắc cộng: Số cách chọn 1 quyển sách bất kì là: \(7 + 5 + 8 = 20\) cách.

Chọn C.

Câu 12:

Phương pháp:

- Sử dụng chỉnh hợp tính số cách chọn số có 3 chữ số đôi một khác nhau.

- Gọi số tự nhiên có 3 chữ số lập được là \(\overline {abc} \).

- Số lần xuất hiện của mỗi số 1, 2, 3, 5, 6 ở mỗi vị trí  \(a,\,\,b,\,\,c\) bằng số cách chọn \(\overline {bc}\) là \(A_4^2 = 12\) lần.

\(\overline {abc} =a.10^2+b.10^1+c\)

Cách giải:

Từ 5 chữ số 1, 2, 3, 5, 6 ta lập được \(A_5^3 = 60\) số có 3 chữ số đôi một khác nhau.

Tổng các chữ số 1, 2, 3, 5, 6 là: \(1 + 2 + 3 + 5 + 6 = 17\).

Gọi số tự nhiên có 3 chữ số lập được là \(\overline {abc} \).

- Trong 60 số lập được ở trên, số lần xuất hiện của mỗi số 1, 2, 3, 5, 6 ở mỗi vị trí  \(a,\,\,b,\,\,c\) là \(A_4^2 = 12\) lần.

 

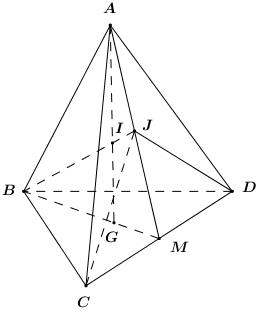
  Chẳng hạn, số lần xuất hiện số 1 ở vị trí \(a\) bằng số cách chọn \(\overline {bc}\) từ 4 số \(2,3,5,6\) và bằng \(A_4^2 = 12\) lần, tương tự  số 1 xuất hiện ở vị trí \(b\) \(A_4^2 = 12\) lần, ở vị trí \(c\) là \(A_4^2 = 12\) lần. 

Vậy tổng của 60 số lập được là: \(12.(1+2+3+5+6).\left( {{{10}^2} + {{10}^1} + {{10}^0}} \right) = 22644\).

Chọn A.

PHẦN II. TỰ LUẬN (7 điểm)

Câu 1:

Phương pháp:

a) Giải phương trình lượng giác cơ bản: \(\sin x = \sin \alpha  \Leftrightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x = \pi  - \alpha  + k2\pi \end{array} \right.\).

b) Giải phương trình dạng \(a\sin x + b\cos x = c\), chia cả 2 vế cho \(\sqrt {{a^2} + {b^2}} \).

Cách giải:

a) \(2\sin \left( {x - \dfrac{\pi }{6}} \right) - \sqrt 3  = 0\)

\(\begin{array}{l} \Leftrightarrow \sin \left( {x - \dfrac{\pi }{6}} \right) = \dfrac{{\sqrt 3 }}{2}\\ \Leftrightarrow \left[ \begin{array}{l}x - \dfrac{\pi }{6} = \dfrac{\pi }{3} + k2\pi \\x - \dfrac{\pi }{6} = \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)

Vậy nghiệm của phương trình là \(x = \dfrac{\pi }{2} + k2\pi ,\,\,x = \dfrac{{5\pi }}{6} + k2\pi \).

b) \(\sin x - \sqrt 3 \cos x =  - \sqrt 2 \)

\(\begin{array}{l} \Leftrightarrow \dfrac{1}{2}\sin x - \dfrac{{\sqrt 3 }}{2}\cos x =  - \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin x\cos \dfrac{\pi }{3} - \cos x\sin \dfrac{\pi }{3} =  - \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x - \dfrac{\pi }{3}} \right) =  - \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \left[ \begin{array}{l}x - \dfrac{\pi }{3} =  - \dfrac{\pi }{4} + k2\pi \\x - \dfrac{\pi }{3} = \dfrac{{5\pi }}{4} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{19\pi }}{{12}} + k2\pi \end{array} \right.\end{array}\)

Vậy nghiệm của phương trình là \(x = \dfrac{\pi }{{12}} + k2\pi ;\,\,x = \dfrac{{19\pi }}{{12}} + k2\pi \).

Câu 2:

Phương pháp:

a) Sử dụng chỉnh hợp.

b) Chia các trường hợp:

    TH1: 3 học sinh nữ, 2 học sinh nam.

    TH2: 4 học sinh nữ, 1 học sinh nam.

    TH3: 5 học sinh nữ.

Cách giải:

a) Từ tập hợp A lập được \(A_7^4 = 840\) số tự nhiên có 4 chữ số khác nhau.

b) Để chọn được 5 học sinh tham gia văn nghệ trong đó có ít nhất 3 học sinh nữ ta có các TH sau:

TH1: 3 học sinh nữ, 2 học sinh nam \( \Rightarrow \) Có \(C_{15}^3.C_{20}^2 = 86450\).

TH2: 4 học sinh nữ, 1 học sinh nam \( \Rightarrow \) Có \(C_{15}^4.C_{20}^1 = 27300\).

TH3: 5 học sinh nữ \( \Rightarrow \) Có \(C_{15}^5 = 3003\).

Vậy có tất cả \(86450 + 27300 + 3003 = 116753\) cách.

Câu 3:

Phương pháp:

1. \({T_{\overrightarrow v }}\left( d \right) = d' \Rightarrow d'//d\), từ đó gọi phương trình đường thẳng \(d'\) có dạng theo phương trình đường thẳng \(d\).

Lấy điểm \(A \in d\) bất kì. Tìm \(A' = {T_{\overrightarrow v }}\left( A \right)\).

Thay tọa độ điểm \(A'\) vào phương trình đường thẳng \(d'\).

2. a) Xác định 2 điểm chung của hai mặt phẳng, từ đó xác định giao tuyến.

b) Xác định \(J\) là giao điểm của \(BI\) và một đường thẳng nằm trong \(\left( {ACD} \right)\).

Sử dụng định lí Menelaus để tính tỉ số.

Cách giải:

 

1. Vì \({T_{\overrightarrow v }}\left( d \right) = d' \Rightarrow d'//d\), do đó phương trình đường thẳng \(d'\) có dạng: \(d':\,\,x + y + c = 0\,\,\left( {c \ne  - 3} \right)\).

Lấy \(A\left( {3;0} \right) \in d\). Gọi \(A' = {T_{\overrightarrow v }}\left( A \right)\), khi đó ta có \(A'\left( {5; - 1} \right)\).

Vì \({T_{\overrightarrow v }}\left( d \right) = d',\,\,A' = {T_{\overrightarrow v }}\left( A \right) \Rightarrow A' \in d'\).

Suy ra \(5 + \left( { - 1} \right) + c = 0 \Leftrightarrow c + 4 = 0 \Leftrightarrow c =  - 4\,\,\left( {TM} \right)\).

Vậy phương trình đường thẳng \(d'\) là: \(x + y - 4 = 0\).

2. a) Xét \(\left( {ABG} \right)\) và \(\left( {ACD} \right)\) có:

+ \(A\) là điểm chung thứ nhất.

+ Trong \(\left( {BCD} \right)\) ta có: \(M = BG \cap CD \Rightarrow \left\{ \begin{array}{l}M \in BG \subset \left( {ABG} \right)\\M \in CD \subset \left( {ACD} \right)\end{array} \right.\) \( \Rightarrow M \in \left( {ABG} \right) \cap \left( {ACD} \right)\).

Vậy \(\left( {ABG} \right) \cap \left( {ACD} \right) = AM\).

b) Trong \(\left( {ABM} \right)\) gọi \(J = BI \cap AM\) ta có:

\(\left\{ \begin{array}{l}J \in BI\\J \in AM \subset \left( {ACD} \right) \Rightarrow J \in \left( {ACD} \right)\end{array} \right.\) \( \Rightarrow J = BI \cap \left( {ACD} \right)\).

Ta có: \(\dfrac{{{S_{JCD}}}}{{{S_{ACD}}}} = \dfrac{1}{2} = \dfrac{{JM}}{{AM}} \Rightarrow \dfrac{{JM}}{{JA}} = 1\).

Áp dụng định lí Menelaus trong tam giác \(AGM\) ta có:

\(\dfrac{{BG}}{{BM}}.\dfrac{{JM}}{{JA}}.\dfrac{{IA}}{{IG}} = 1 \Leftrightarrow \dfrac{2}{3}.1.\dfrac{{IA}}{{IG}} = 2 \Leftrightarrow \dfrac{{IA}}{{IG}} = 3\)  \( \Rightarrow \dfrac{{AI}}{{AG}} = \dfrac{3}{4}\).

Vậy để \({S_{ACD}} = 2{S_{JCD}}\) thì \(\dfrac{{AI}}{{AG}} = \dfrac{3}{4}\).

HocTot.Nam.Name.Vn