Đề kiểm tra giữa học kì 2 Vật lí 10 - Đề số 03 có lời giải chi tiết

Đề bài

I – TRẮC NGHIỆM (2 điểm)

Câu 1: Biểu thức nào không phải là công suất:

A. \(F.s\)                 B. \(\frac{A}{t}\)

C. \(F.\frac{s}{t}\)                 D. \(F.v\)

Câu 2: Một gàu nước có khối lượng 20kg được kéo cho chuyển động đều lên cao 5m trong thời gian 1 phút 4 giây. Lấy \(g = 10m/{s^2}\). Công suất trung bình của lực kéo là:

A. \(100W\)                            B. \(10W\)

C. \(1W\)                                D. \(30W\)

Câu 3: Một ô tô chạy trên đường nằm ngang với vận tốc \(v = 72km/h\). Công suất của động cơ là P = 60kW. Lực phát động của động cơ là:

A. 3000N                               B. 2800N

C. 3200N                               D. 2500N

Câu 4: Một thang máy có khối lượng m = 3 tấn đi lên với gia tốc \(a = 1m/{s^2}\). Trong thời gian 4 giây đầu tiên công suất của thang máy là: (cho \(g = 10m/{s^2}\)).

A. 33kW                                 B. 66kW

C. 5,5kW                                D. 45kW

Câu 5: Một cần cẩu nâng một vật có khối lượng 2 tấn làm cho vật chuyển động nhanh dần đều theo phương thẳng đứng lên cao \(12,5m\) với gia tốc \(1m/{s^.}^2\). Lấy \(g = 10m/{s^2}\). Hãy tính công mà cần cầu thực hiện và công suất trung bình của cần cẩu ấy.

A. \(275000{\rm{ }}J;{\rm{ }}55kW\)

B. \(35000J;{\rm{ }}50kW\)

C. \(4500J;{\rm{ }}60W\)

D. \(300000J;{\rm{ }}65kW\)

Câu 6: Một ô tô đang leo dốc, nếu công suất của động cơ không đổi thì vận tốc của ô tô sẽ giảm đi vì:

A. Để lực kéo tăng.

B. Để lực kéo giảm.              

C. Để lực kéo không đổi.

D. Để động cơ chạy êm.

Câu 7: Véc tơ động lượng là véc tơ:

A. Cùng phương, ngược chiều với véc tơ vận tốc

B. Có phương hợp với véc tơ vận tốc một góc \(\alpha \) bất kỳ.

C. Có phương vuông góc với véc tơ vận tốc.

D. Cùng phương, cùng chiều với véc tơ vận tốc.

Câu 8: Một vật khối lượng \(m = 3kg\) được kéo lên trên mặt phẳng nghiêng một góc \({30^0}\) so với phương ngang bởi một lực không đổi \(F = 50N\) dọc theo đường chính. Hãy xác định công do từng lực thực hiện với độ dời \(s = 1,5m\). Bỏ qua ma sát của chuyển động. Lấy \(g = 10m/{s^2}\).

A. \({A_k} = 75J;{\mkern 1mu} {A_P} = 22,5J;{\mkern 1mu} {A_N} = 10J\)  

B. \({A_k} =  - 95J;{\mkern 1mu} {A_P} =  - 22,5J;{\mkern 1mu} {A_N} = 20J\)         

C. \({A_k} = 75J;{\mkern 1mu} {A_P} =  - 22,5J;{\mkern 1mu} {A_N} = 0\)

D. \({A_k} = 85J;{\mkern 1mu} {A_P} =  - 12,5J;{\mkern 1mu} {A_N} = 0\)

II –  TỰ LUẬN (8 điểm)

Câu 1 (1 điểm):

Một thang máy có khối lượng 1,5 tấn chuyển động từ tầng cao nhất cách mặt đất \(120m\) xuống tầng thứ 10 cách mặt đất 40m. Nếu chọn gốc thế năng tại tầng 10, lấy \(g = 9,8m/{s^2}\). Thế năng của thang máy ở tầng cao nhất là:

 A. 1176 kJ.                            B. 1392 kJ.

C.  980 kJ.                              D. 1588 J. 

Câu 2 (1 điểm):

Định nghĩa và viết biểu thức tính công suất.

Câu 3 (1,5 điểm):

Một hệ gồm hai vật có khối lượng và độ lớn vận tốc lần lượt là \({m_1} = 2kg,{v_1} = 3m/s\) và

\({m_2} = 1kg,{v_2} = 6m/s\). Tìm tổng động lượng của hệ trong các trường hợp:

a) Hai vật chuyển động theo hai hướng hợp với nhau góc \(\alpha  = {60^0}\)

b) Hai vật chuyển động theo hai hướng hợp với nhau góc \(\alpha  = {120^0}\)

Câu 4 (1,5 điểm):

Một viên đạn khối lượng 1kg đang bay theo phương thẳng đứng với vận tốc \(500m/s\) thì nổ thành hai mảnh có khối lượng bằng nhau. Mảnh thứ nhất bay theo phương ngang với vận tốc \(500\sqrt 2 m/s\). Hỏi mảnh thứ 2 bay theo phương nào với vận tốc bao nhiêu?

A.  Mảnh thứ 2 bay theo phương hợp với phương thẳng đứng góc \({35^0}\)với vận tốc \(1225m/s\)      

B.  Mảnh thứ 2 bay theo phương hợp với phương thẳng đứng góc \({30^0}\)  với vận tốc \(1225m/s\)     

C.  Mảnh thứ 2 bay theo phương hợp với phương thẳng đứng góc \({35^0}\)  với vận tốc 1415m/s         

D.  Mảnh thứ 2 bay theo phương hợp với phương thẳng đứng góc \({30^0}\)với vận tốc \(1415m/s\)

Câu 5 (3 điểm):

Một xe tải có khối lượng 1 tấn, bắt đầu chuyển động nhanh dần đều từ A trên một đường thẳng nằm ngang \(AB = 200m\), biết rằng khi xe đến B đạt vận tốc \(20m/s\), hệ số ma sát giữa bánh xe và mặt đường là \(0,1\).

a) Tính độ lớn công của lực kéo động cơ trên đoạn đường AB.

b) Đến B, xe tắt máy và tiếp tục xuống dốc nghiêng BC hợp với mặt phẳng nằm ngang góc \({30^0}\). Biết \(BC = 100m\), hệ số ma sát trên đoạn BC là \(\frac{1}{{5\sqrt 3 }}\) . Xác định động lượng của xe tại chân dốc. 

Lời giải chi tiết

1. A	2. B	3. A	4. B
5. A	6. A	7. D	8. C

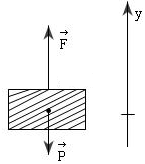
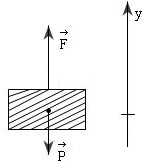
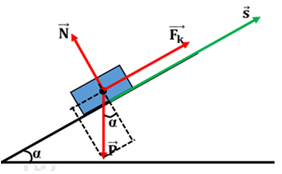
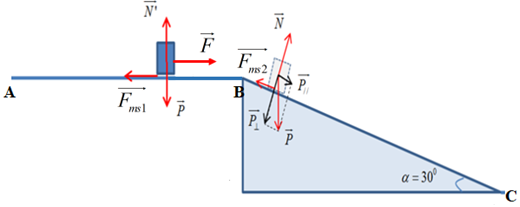
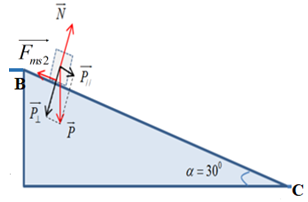
I – TRẮC NGHIỆM (2 điểm)

Câu 1:

Phương pháp:

Công suất: \(P = \frac{A}{t} = \frac{{F.s}}{t} = F.v\)

Cách giải:

Biểu thức \(F.s\) không phải là công suất.

Chọn A.

Câu 2:

Phương pháp:

Công suất: \(P = \frac{A}{t} = \frac{{F.s}}{t} = \frac{{P.h}}{t}\)

Cách giải:

Ta có: \(\left\{ \begin{array}{l}t = 1phut40s = 100s\\h = 5m\end{array} \right.\)

Lực tác dụng vào gàu nước: \(F = P = mg = 10.20 = 200N\)

Công suất trung bình của lực kéo:\(P = \frac{A}{t} = \frac{{F.s}}{t} \\= \frac{{P.h}}{t} = \frac{{200.5}}{{100}} \\= 10W\)

Chọn B.

Câu 3:

Phương pháp:

Công thức tính công suất: \(P = \frac{A}{t} = \frac{{F.s}}{t} = F.v\)

Cách giải:

Ta có: \(\left\{ \begin{array}{l}v = 72km/h = 20m/s\\P = 60kW \\= 60000W\end{array} \right.\)

Công suất được xác định bởi công thức:\(P = F.v \Rightarrow F = \frac{P}{v}\\ = \frac{{60000}}{{20}} = 3000N\)

Chọn A.

Câu 4:

Phương pháp:

Sử dụng định luật II Niuton tính được lực kéo thang máy.

Công thức tính quãng đường: \(s = {v_0}t + \frac{1}{2}a{t^2}\)

Công thức tính công của lực: \(A = F.s.cos\left( {\overrightarrow F ;\overrightarrow s } \right)\)

Công thức tính công suất: \(P = \frac{A}{t}\)

Cách giải:

Ta có: \(\left\{ \begin{array}{l}m = 3T = 3000kg\\a = 1m/{s^2}\\g = 10m/{s^2}\\t = 4s\end{array} \right.\)

Biểu diễn các lực tác dụng lên thang máy:

Áp dụng định luật II Niuton ta có: \(\overrightarrow F  + \overrightarrow P  = m.\overrightarrow a \,\,\left( * \right)\)

Chiếu (*) lên Oy ta có:

\(F - P = ma \Rightarrow F = P + ma\\ = m\left( {g + a} \right)\\ \Rightarrow F = 3000.\left( {10 + 1} \right) \\= 33000N\)

Quãng đường vật đi được trong 4s đầu tiên là:

\(s = {v_0}t + \frac{1}{2}a{t^2} = 0 + \frac{1}{2}{.1.4^2} = 8m\)

Công của lực kéo thang trong 4s đầu:

\(A = F.s.\cos \left( {\overrightarrow F ;\overrightarrow s } \right) \\= 33000.8.\cos 0 = 264\,000J\)

Công suất trung bình của lực kéo thang: \(P = \frac{A}{t} = \frac{{264000}}{4} \\= 66000W = 66kW\)

Chọn B.

Câu 5:

Phương pháp:

Sử dụng định luật II Niuton tính được lực kéo thang máy.

Công thức tính công của lực: \(A = F.s.cos\left( {\overrightarrow F ;\overrightarrow s } \right)\)

Công thức tính quãng đường: \(s = {v_0}t + \frac{1}{2}a{t^2}\\ \Rightarrow t\)

Công thức tính công suất: \(P = \frac{A}{t}\)

Cách giải:

Ta có: \(\left\{ \begin{array}{l}m = 2T = 2000kg\\s = h = 12,5m\\a = 1m/{s^2}\\g \\= 10m/{s^2}\end{array} \right.\)

Biểu diễn các lực tác dụng vào thang máy trên hình:

Áp dụng định luật II Niuton ta có: \(\overrightarrow F  + \overrightarrow P  = m.\overrightarrow a \,\,\left( * \right)\)

Chiếu (*) lên Oy ta có:

\(F - P = ma \Rightarrow F = P + ma = m\left( {g + a} \right) \\\Rightarrow F = 2000.\left( {10 + 1} \right) = 22000N\)

Công mà cần cẩu thực hiện: \(A = F.s = 22000.12,5 = 275000J\)

Lại có quãng đường vật đi được trong 12,5m là:

\(s = {v_0}t + \frac{1}{2}a{t^2} \Leftrightarrow 12,5 = 0 + \frac{1}{2}.1.{t^2}\\ \Rightarrow t = 5s\)

Công suất trung bình của cần cẩu: \(P = \frac{A}{t} = \frac{{275000}}{5}\\ = 55000W = 55kW\)

Chọn A.

Câu 6:

Phương pháp:

Công thức tính công suất: \(P = \frac{A}{t} = \frac{{F.s}}{t} = F.v\)

Cách giải:

Ta có: \(P = F.v\) \( \Rightarrow \) v giảm thì F tăng.

\( \Rightarrow \) Một ô tô đang leo dốc, nếu công suất của động cơ không đổi thì vận tốc của ô tô sẽ giảm đi để tăng lực kéo giúp ô tô leo được dốc.

Chọn A.

Câu 7:

Phương pháp:

Động lượng \(\overrightarrow p \) của một vật là một vecto cùng hướng với vận tốc của vật và được xác định bởi công thức \(\overrightarrow p  = m.\overrightarrow v \).

Cách giải:

Ta có: \(\overrightarrow p  = m.\overrightarrow v \)

\( \Rightarrow \) Vecto động lượng là vecyo cùng phương, cùng chiều với vecto vận tốc.

Chọn D.

Câu 8:

Phương pháp:

Công thức tính công: \(A = F.s.\cos \alpha \)

Cách giải:

+ Vật chịu tác dụng của ba lực: Trọng lực \(\vec P\);  phản lực \(\vec N\) của mặt phẳng nghiêng; lực kéo \(\overrightarrow {{F_k}} \)

+ Công của lực kéo \(\overrightarrow {{F_k}} \) là: \({A_k} = {F_k}.s.\cos {0^0} = 50.1,5.1 = 75J\)

+ Công của trọng lượng \(\vec P\)là:

\(\begin{array}{*{20}{l}}{{A_P} = P.s.\cos \left( {\vec P;\vec s} \right) = P.s.\cos \left( {{{90}^0} + \alpha } \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}  = P.s.\cos \left( {{{90}^0} + \alpha } \right) \\= m.g.s\cos \left( {{{90}^0} + \alpha } \right) = 3.10.1,5.\cos 120\\ =  - 22,5J}\end{array}\)

+ Công của phản lực N: \({A_N} = N.s.\cos {90^0} = 0\)

Chọn C.

II –  TỰ LUẬN (8 điểm)

Câu 1:

Phương pháp:

Thế năng trọng trường: \({{\rm{W}}_t} = mgz\)

Cách giải:

Chọn gốc thế năng tại tầng 10.

Khoảng cách từ tầng cao nhất đến gốc thế năng là: \(z = 120 - 40 = 80m\)

Thế năng của thang máy ở tầng cao nhất là:

\({{\rm{W}}_t} = mgz = 1,5.1000.9,8.80\\ = 1{\mkern 1mu} 176{\mkern 1mu} 000J\\ = 1{\mkern 1mu} 176kJ\)

Chọn A.

Câu 2:

Phương pháp:

Sử dụng lí thuyết “Bài 24: Công và công suất – Trang 128 – SGK Vật Lí 10”.

Cách giải:

+ Công suất là đại lượng đo bằng công sinh ra trong một đơn vị thời gian.

+ Biểu thức tính công suất: \(P = \frac{A}{t}\)

Câu 3:

Phương pháp:

+ Động lượng \(\overrightarrow p \) của một vật là một vecto cùng hướng với vận tốc của vật và được xác định bởi công thức \(\overrightarrow p  = m.\overrightarrow v \).

+ Tổng động lượng: \(\overrightarrow p  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \)

Độ lớn: \(p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \alpha } \)

Cách giải:

Ta có: \(\left\{ \begin{array}{l}{m_1} = 2kg;{v_1} = 3m/s\\{m_2} = 1kg;{v_2} = 6m/s\end{array} \right. \\\Rightarrow \left\{ \begin{array}{l}{p_1} = {m_1}{v_1} = 6kg.m/s\\{p_2}\\ = {m_2}{v_2} = 6kg.m/s\end{array} \right.\)

Tổng động lượng: \(\overrightarrow p  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \)

a) Với \(\alpha  = {60^0}\)

\( \Rightarrow p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \alpha } \\ = \sqrt {{6^2} + {6^2} + 2.6.6.cos60}  \\= 6\sqrt 3 kg.m/s\)

b) Với \(\alpha  = {120^0}\)

\( \Rightarrow p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \alpha } \\ = \sqrt {{6^2} + {6^2} + 2.6.6.cos120}  \\= 6kg.m/s\)

Câu 4:

Phương pháp:

Động lượng của một vật khối lượng m đang chuyển động với vận tốc \(\vec v\) là đại lượng được xác định bởi công thức: \(\vec p = m\vec v\)

Định luật bảo toàn động lượng: Động lượng của một hệ cô lập là một đại lượng bảo toàn

Cách giải:

\(\begin{array}{*{20}{l}}{m = 1kg;v = 500m/s}\\{{m_1} = {m_2} = \frac{m}{2} = 0,5kg;\\{v_1} = 500\sqrt 2 m/s}\end{array}\)

 Xét hệ gồm hai mảnh đạn trong thời gian nổ.

Động lượng của hệ trước khi đạn nổ: \(\vec p = m.\vec v\)

Động lượng sau khi đạn nổ: \(\vec p' = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \\ = {m_1}.\overrightarrow {{v_1}}  + {m_2}.\overrightarrow {{v_2}} \)

Áp dụng định luật bảo toàn động lượng ta có: \(\vec p = \vec p' \\\Rightarrow \vec p = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \)

Viên đạn đang bay theo phương thẳng đứng thì nổ thành hai mảnh mảnh thứ nhất bay theo phương ngang.

Ta có hình vẽ:

Từ hình vẽ ta có:

\(\begin{array}{*{20}{l}}{p_2^2 = {p^2} + p_1^2 \Leftrightarrow {{\left( {\frac{m}{2}.{v_2}} \right)}^2} = {{\left( {mv} \right)}^2} + {{\left( {\frac{m}{2}.{v_1}} \right)}^2}}\\{ \Rightarrow v_2^2 = 4{v^2} + v_1^2 = {{4.500}^2} + {{\left( {500\sqrt 2 } \right)}^2}\\ \Rightarrow {v_2} = 1225m/s}\end{array}\)

Góc hợp bởi giữa \(\overrightarrow {{v_2}} \) và phương thẳng đứng là: \(\sin \alpha  = \frac{{{p_1}}}{{{p_2}}} = \frac{{{v_1}}}{{{v_2}}} \\= \frac{{500\sqrt 2 }}{{1225}}\\ \Rightarrow \alpha  = {35^0}\)

Chọn A

Câu 5:

Phương pháp:

Sử dụng định luật II Niuton.

Công thức tính công: \(A = F.s.cos\left( {\overrightarrow F ;\overrightarrow s } \right)\)

Công thức tính gia tốc: \(a = \frac{{{v^2} - v_0^2}}{{2s}}\)

Động lượng: \(\overrightarrow p  = m\overrightarrow v \)

Cách giải:

Ta có: \(\left\{ \begin{array}{l}m = 1T = 1000kg\\{v_A} = 0\\{v_B} = 20m/s\\AB = 200m\\{\mu _{AB}} \\= 0,1\end{array} \right.\)

Biểu diễn các lực tác dụng vào vật trên hình vẽ:

a) Xét trên đoạn đường AB:

Gia tốc của xe : \(a = \frac{{v_B^2 - v_A^2}}{{2.BC}} = \frac{{{{20}^2} - {0^2}}}{{2.200}}\\ = 1m/{s^2}\)

Áp dụng định luật II Niuton ta có: \(\overrightarrow {{F_{ms1}}}  + \overrightarrow N  + \overrightarrow P  + \overrightarrow F  = m.\overrightarrow a \,\,\,\left( * \right)\)

Chiếu (*) lên phương chuyển động ta có:

\(\begin{array}{l} - {F_{ms1}} + F = ma \Rightarrow F = {F_{ms1}} + ma \\= \mu mg + ma\\ \Rightarrow F = 0,1.1000.10 + 1000.1 \\= 2000N\end{array}\)

Độ lớn công của lực kéo động cơ:

\(A = F.AB.cos\left( {\overrightarrow F ;\overrightarrow {AB} } \right) \\= 2000.200.cos0 = 400\,000J\)

b) Xét trên đoạn đường BC:

Ta có: \(\left\{ \begin{array}{l}\alpha  = {30^0}\\BC = 100m\\{\mu _{BC}}\\ = \frac{1}{{5\sqrt 3 }}\end{array} \right.\)

 

Áp dụng định luật II Niuton ta có: \(\overrightarrow {{F_{ms2}}}  + \overrightarrow N  + \overrightarrow P  = m\overrightarrow {a'} \,\,\left( {**} \right)\)

Chiếu (**) lên các trục tọa độ ta có:

\(\begin{array}{l}\left\{ \begin{array}{l} - {F_{ms2}} = ma\\N = P.\cos \alpha \end{array} \right. \Rightarrow  - {\mu _{BC}}.mg.cos\alpha  = ma'\\ \Rightarrow a' =  - {\mu _{BC}}g.cos\alpha  =  - \frac{1}{{5\sqrt 3 }}.10.cos30 \\=  - 1m/{s^2}\end{array}\)

Lại có \(v_C^2 - v_B^2 = 2a'.BC\)

\( \Rightarrow v_C^2 = v_B^2 + 2a'.BC = {20^2} + 2.\left( { - 1} \right).100 = 200\\ \Rightarrow {v_C} = 10\sqrt 2 m/s\)

Động lượng của xe tại chân dốc là:

\({p_C} = m.{v_C} = 1000.10\sqrt 2  \\= 10000\sqrt 2 \,\left( {kgm/s} \right)\).

HocTot.Nam.Name.Vn