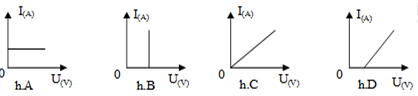
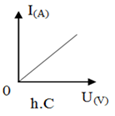
Đề kiểm tra giữa học kì 1 Vật lí 9 - Đề số 05 có lời giải chi tiết

Đề bài

PHẦN I – TRẮC NGHIỆM (5đ)

Câu 1: Đồ thị biểu diễn mối quan hệ giữa cường độ dòng điện (I) chạy trong dây dẫn với hiệu điện thế  (U) giữa hai đầu dây dẫn đó là?

 

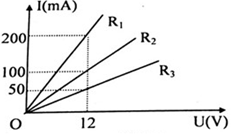
A. Hình A                              B. Hình B

C. Hình C                              D. Hình D

Câu 2: Dòng điện đi qua một dây dẫn có dòng điện \({I_1}\)  khi hiệu điện thế giữa hai đầu dây dẫn là \(12V\). Để dòng điện này có cường độ \({I_2}\)  nhỏ hơn \({I_1}\)  một lượng \(0,6{I_1}\;\) thì phải đặt giữa hai đầu dây này một hiệu điện thế bao nhiêu?

A. 19,2V                                B. 4,8V

C. 11,4V                                D. 7,2V

Câu 3: Trên hình 1 là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện và hiệu điện thế đối với 1 dây dẫn khác nhau. Dựa vào đồ thị cho biết điện trở \({R_1},{\rm{ }}{R_2},{\rm{ }}{R_3}\)  có giá trị là: 

 

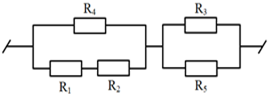
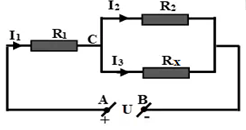
A. \({R_{1\;}} = 20\Omega ;{R_{2\;}} = 120\Omega ;{R_{3\;}} = 60\Omega \)

B. \({R_{1\;}} = 12\Omega ;{R_{2\;}} = 8,3\Omega ;{R_{3\;}} = 4,16\Omega \)

C. \({R_{1\;}} = 60\Omega ;{R_{2\;}} = 120\Omega ;{R_{3\;}} = 240\Omega \)

D. \({R_{1\;}} = 30\Omega ;{R_{2\;}} = 120\Omega ;{R_{3\;}} = 60\Omega \)

Câu 4: Công thức biểu thị định luật Ôm là

A. \(R = \dfrac{U}{I}\)

B. \(I = \dfrac{R}{U}\)

C. \(I = \dfrac{U}{R}\)

D. \(R = \dfrac{I}{U}\)

Câu 5: Đặt một hiệu điện thế \(U = 12V\) vào hai đầu đoạn mạch gồm điện trở \({R_1}\; = 40\Omega \) mắc nối tiếp với điện trở \({R_2}\; = 80\Omega \) . Hiệu điện thế ở hai đầu điện trở R1 bằng

A. 6V.                                    B. 4V. 

C. 8V.                                    D. 12V.

Câu 6: Hai điện trở \({R_1}\; = 5\Omega \) và  \({R_2}\; = 10\Omega \) mắc nối tiếp. Cường độ dòng điện qua điện trở \({R_1}\)  là \(4A\).

Thông tin nào SAI.

A. Điện trở tương đương của mạch là \(15\Omega \)

B. Cường độ dòng điện qua \({R_2}\)là \({I_2}\; = 8A\)

C. Hiệu điện thế hai đầu đoạn mạch là \(60V\)

D. Hiệu điện thế hai đầu \({R_1}\)  là  \(20V\)

Câu 7: Mắc nối tiếp hai điện trở \({R_1}\)  và \({R_2}\) \(\left( {{R_1}\; > {R_2}} \right)\) với nhau thành một đoạn mạch. Điện trở \(R\) của đoạn mạch thoả mãn:

A. \(R < {R_2}\)                    B. \(R \ge {R_1}\)

C. \(R > {R_1}\)                    D. \(R \le {R_2}\)

Câu 8: Công thức nào dưới đây là đúng đối với đoạn mạch gồm hai điện trở  \({R_1}\)  và  \({R_2}\) mắc song song?

A. \(I = {I_1} + {I_2}\)

B.  \(I = {I_1} = {I_2}\)

C. \(\frac{{{I_1}}}{{{I_2}}} = \frac{{{R_1}}}{{{R_2}}}\)

D. \(\frac{{{I_1}}}{{{I_2}}} = \frac{{{U_2}}}{{{U_1}}}\)

Câu 9: Ba bóng đèn có điện trở bằng nhau, chịu được hiệu điện thế định mức 6V. Phải mắc ba bóng đèn theo kiểu nào vào hai điểm có hiệu điện thế 18V để chúng sáng bình thường?

A. ba bóng mắc song song

B. hai bóng song song, bóng thứ ba nối tiếp với hai bóng trên

C. hai bóng nối tiếp, bóng còn lại song song với cả hai bóng trên

D. ba bóng mắc nối tiếp nhau

Câu 10: Cho mạch điện như hình vẽ.  \({R_1} = {R_3} = {R_5} = 2\Omega ;{\mkern 1mu} {\mkern 1mu} {R_2} = 4\Omega ;{\mkern 1mu} {\mkern 1mu} {R_4} = 6\Omega \). Tính điện trở tương đương của mạch

 

A. \(10\Omega \)                    B. \(5\Omega \)

C. \(4\Omega \)                      D. \(6\Omega \)

Câu 11: Điện trở tương đương của đoạn mạch AB có sơ đồ như trên hình vẽ là \({R_{AB}}\; = 10\Omega \), trong đó các điện trở \({R_1}\; = 7\Omega {\rm{ }};{R_2}\; = 12\Omega \). Hỏi điện trở \({R_x}\)  có giá trị nào dưới đây?

 

A. \(9\Omega \)                      B. \(5\Omega \)

C. \(4\Omega \;\;\)                  D. \(15\Omega \)

Câu 12: Điện trở của dây dẫn không phụ thuộc vào yếu tố nào dưới đây?

A. Vật liệu làm dây dẫn

B. Khối lượng của dây dẫn

C. Chiều dài dây dẫn

D. Tiết diện của dây dẫn

Câu 13: Một đoạn dây dẫn hình trụ, đồng chất, tiết diện đều có điện trở là \(R\) . Nếu cắt đoạn dây đó thành bốn đoạn có chiều dài bằng nhau thì mỗi đoạn có điện trở là

A. \(0,25R\)                            B. \(2R\)

C. \(0,5R\)                              D. \(4R\)

Câu 14: Hiệu điện thế U trong mạch điện có sơ đồ như hình vẽ được giữ không đổi. Khi dịch chuyển con chạy của biến trở tiến dần về đầu N thì số chỉ của ampe kế sẽ thay đổi như thế nào?

 

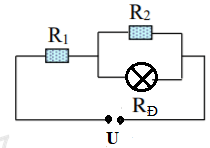
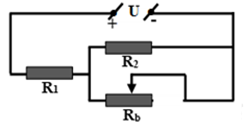
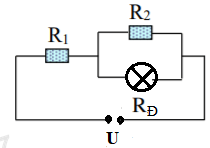
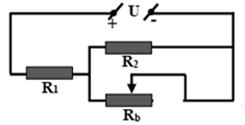
A. Giảm dần đi 

B. Tăng dần lên.

C. Không thay đổi. 

D. Lúc đầu giảm dần đi, sau đó tăng dần lên.

Câu 15: Cho mạch điện như hình vẽ, U không đổi. Để đèn sáng mạnh hơn thì phải dịch chuyển con chạy C về phía:

 

A. gần M, để chiều dài dây dẫn của biến trở giảm.

B. gần M, để chiều dài phần dây dẫn có dòng điện chạy qua giảm.

C. gần M, để hiệu điện thế giữa hai đầu biến trở tăng.

D. gần M, để hiệu điện thế giữa hai đầu bóng đèn và hai đầu biến trở cùng tăng.

Câu 16: Biến trở là một dụng cụ dùng để

A. Thay đổi vật liệu trong vật dẫn.

B. Điều chỉnh hiệu điện thế giữa hai đầu đoạn mạch.

C. Thay đổi khối lượng riêng của dây dẫn.

D. Điều chỉnh cường độ dòng điện trong mạch.

Câu 17: Trong các biểu thức sau đây, biểu thức nào là biểu thức của định luật Jun – Len-xơ?

A. \(Q = I.R.t\)

B. \(Q = {I^2}.R.t\)

C. \(Q = {R^2}.I.t\)

D. \(Q = {I^2}.{R^2}.t\)

Câu 18: Trong gia đình, các thiết bị nung nóng bằng điện năng. Biện pháp tiết kiệm nào dưới đây là hợp lí nhất?

A. Không sử dụng các thiết bị nung nóng bằng điện.

B. Không đun nóng bằng bếp điện.

C. Chỉ sử dụng các thiệt bị nung nóng bằng điện có công suất nhỏ trong thời gian tốì thiểu cần thiết.

D. Chỉ đun nấu bằng điện và sử dụng các thiết bị nung nóng khác như bàn là, máy sấy tóc,... trong thời gian tối thiểu cần thiết.

Câu 19: Đơn vị của công suất điện là:

A. \(J\)                                    B. \(W\)

C. \(Wh\)                                D. \(kWh\)

Câu 20: Một bóng đèn loại \(220V-100W\) và một bếp điện loại \(220V-1000W\) được sử dụng ở hiệu điện thế định mức, mỗi ngày trung bình đèn sử dụng 5 giờ, bếp sử dụng 2 giờ. Giá \(1KWh\) điện 2.000 đồng. Tính tiền điện phải trả của 2 thiết bị trên trong 30 ngày?

A. 150.000 đồng 

B. 300.000 đồng                    

C. 500.000 đồng

D. 66.0000 đồng

PHẦN II – TỰ LUẬN (5đ)

Câu 21: (2đ) Một bình nóng lạnh có ghi \(220V-1100W\) được sử dụng với hiệu điện thế \(220V\)

a) Tính cường độ dòng điện chạy qua bình khi đó

b) Tính thời gian để bình đun sôi 10 lít nước từ nhiệt độ \({20^0}C\), biết nhiệt dung riêng của nước là \(4200J/kg.K\) và nhiệt lượng bị hao phí là rất nhỏ

c) Tính tiền điện phải trả cho việc sử dụng bình như trên trong 30 ngày, biết rằng thời gian sử dụng trung bình mỗi ngày là 1 giờ, và giá tiền điện là  

Câu 22: (2đ) Cho mạch điện gồm \({R_1}{\mkern 1mu} {\mkern 1mu} nt{\mkern 1mu} {\mkern 1mu} \left( {{R_2}//{R_D}} \right)\), \({U_{AB}} = 12V,{R_1} = 3\Omega ,{R_2} = 6\Omega \) , đèn Đ có điện trở \({R_D} = 6\Omega .\)

 

a) Tính điện trở tương đương của đoạn mạch AB.

b) Đóng khóa K, xác định số chỉ ampe kế và độ sáng của đèn Đ. Biết hiệu điện thế ghi trên bóng đèn là  6V .

c) Tháo bỏ điện trở \({R_2}\) khỏi mạch điện, hãy cho biết khi đó số chỉ của ampe kế và độ sáng của đèn Đ thay đổi như thế nào? Giải thích.

Câu 23: (1đ) Một biến trở \({R_b}\)  có giá trị lớn nhất là \(30\Omega \)  được mắc với hai điện trở \({R_1}\; = 15\Omega \) và  \({R_2}\; = 10\Omega \) thành hai đoạn mạch có sơ đồ như hình vẽ, trong đó hiệu điện thế không đổi \(U = 4,5V\). Hỏi khi điều chỉnh biến trở thì cường độ dòng điện chạy qua biến trở \({R_1}\)  có giá trị lớn nhất \({I_{max}}\)  và nhỏ nhất \({I_{min}}\)  là bao nhiêu?

Lời giải chi tiết

1.C	2.B	3.C	4.C	5.B	6.B	7.C	8.A	9.D	10.C
11.C	12.B	13.A	14.A	15.B	16.D	17.B	18.D	19.B	20.A

Câu 1:

Phương pháp giải:

- Cường độ dòng điện chạy qua một dây dẫn tỉ lệ thuận với hiệu điện thế đặt vào hai đầu dây dẫn đó

- Đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện vào hiệu điện thế giữa hai đầu dây dẫn là một đường thẳng đi qua gốc toạ độ (U = 0; I = 0)

Lời Giải:

Đồ thị biểu diễn mối quan hệ giữa cường độ dòng điện (I) chạy trong dây dẫn với hiệu điện thế  (U) giữa hai đầu dây dẫn là:

 

Chọn C.

Câu 2:

Phương pháp giải:

Cường độ dòng điện chạy qua một dây dẫn tỉ lệ thuận với hiệu điện thế đặt vào hai đầu dây dẫn đó.

Lời Giải:

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\frac{{{U_1}}}{{{U_2}}} = \frac{{{I_1}}}{{{I_2}}}}\\{{I_2} = {I_1} - 0,6{I_1} = 0,4{I_1}}\end{array}} \right. \\\Rightarrow \frac{{12}}{{{U_2}}} = \frac{{{I_1}}}{{0,4,{I_1}}} \Rightarrow {U_2} = 4,8V\)

Chọn B.

Câu 3:

Phương pháp giải:

Định luật Ôm: Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế đặt vào hai đầu dây và tỉ lệ nghịch với điện trở của dây: \(I = \frac{U}{R}\)

Lời Giải:

Từ đồ thị ứng với hiệu điện thế \(U = 12V\) ta có: \(\left\{ {\begin{array}{*{20}{l}}{{I_1} = 200mA = 0,2A}\\{{I_2} = 100mA = 0,1A}\\{{I_3} = 50mA = 0,05A}\end{array}} \right.\)

Áp dụng định luật Ôm ta có: \(\left\{ {\begin{array}{*{20}{l}}{{R_1} = \frac{U}{{{I_1}}} = \frac{{12}}{{0,2}} = 60\Omega }\\{{R_2} = \frac{U}{{{I_2}}} = \frac{{12}}{{0,1}} = 120\Omega }\\{{R_3} = \frac{U}{{{I_3}}} = \frac{{12}}{{0,05}} = 240\Omega }\end{array}} \right.\)

Chọn C.

Câu 4:

Phương pháp giải:

Định luật Ôm: Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế đặt vào hai đầu dây và tỉ lệ nghịch với điện trở của dây:  \(I = \frac{U}{R}\)

Lời Giải:

Công thức biểu thị định luật Ôm là:  \(I = \frac{U}{R}\)

Chọn C.

Câu 5:

Phương pháp giải:

Công thức của mạch nối tiếp: \(\left\{ {\begin{array}{*{20}{l}}{U = {U_1} + {U_2}}\\{I = {I_1} = {I_2}}\\{R = {R_1} + {R_2}}\end{array}} \right.\)

Định luật Ôm: \(I = \frac{U}{R}\)

Lời Giải:

Mạch gồm \({R_1}\,nt\,{R_2}\) nên:

\(I = {I_1} = {I_2} = \frac{U}{{{R_{td}}}} = \frac{U}{{{R_1} + {R_2}}} \\= \frac{{12}}{{40 + 80}} = 0,1A\)

Hiệu điện thế ở hai đầu điện trở \({R_1}\) : \({U_1} = {I_1}{R_1} = 0,1.40 = 4V\)

Chọn B.

Câu 6:

Phương pháp giải:

Công thức của mạch nối tiếp: \(\left\{ {\begin{array}{*{20}{l}}{I = {I_1} = {I_2}}\\{U = {U_1} + {U_2}}\\{{R_{td}} = {R_1} + {R_2}}\end{array}} \right.\)

Hệ thức định luật Ôm: \(I = \frac{U}{R} \Rightarrow U = I.R\)

Lời Giải:

Ta có : \(\left\{ {\begin{array}{*{20}{l}}{{R_{td}} = {R_1} + {R_2} = 5 + 10 = 15\Omega }\\{I = {I_1} = {I_2} = 4A}\\{U = I.{R_{td}} = 4.15 = 60V}\\{{U_1} = {I_1}{R_1} = 4.5 = 20V}\end{array}} \right.\)

\( \Rightarrow \) Thông tin sai là: Cường độ dòng điện qua \({R_2}\)  là \({I_{2\;}} = 8A\)

Chọn B.

Câu 7:

Phương pháp giải:

Điện trở tương đương của đoạn mạch nối tiếp: \({R_{td}} = {R_1}\; + {\rm{ }}{R_2}\)

Lời Giải:

Ta có:  \(\left\{ {\begin{array}{*{20}{l}}{R = {R_1} + {R_2}}\\{{R_1} > {R_2}}\end{array}} \right. \Rightarrow R > {R_1}\)

Chọn C.

Câu 8:

Phương pháp giải:

Vận dụng các biểu thức về mạch gồm 2 điện trở mắc song song: \(\left\{ \begin{array}{l}{U_1} = {U_2} = U\\I = {I_1} + {I_2}\\\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\end{array} \right.\)

Lời Giải:

Các công thức của mạch điện gồm 2 điện trở mắc song song: \(\left\{ \begin{array}{l}{U_1} = {U_2} = U\\I = {I_1} + {I_2}\\\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\end{array} \right.\)

A – đúng

B – sai vì:  \(I = {I_1} + {I_2}\)

C – sai vì:  \({U_1} = {U_2} \Leftrightarrow {I_1}{R_1} = {I_2}{R_2} \Rightarrow \frac{{{I_1}}}{{{I_2}}} = \frac{{{R_2}}}{{{R_1}}}\)

D – sai vì:  \(\frac{{{U_2}}}{{{U_1}}} = \frac{{{I_2}{R_2}}}{{{I_1}{R_1}}}\)

Chọn A.

Câu 9:

Phương pháp giải:

Công thức của mạch mắc nối tiếp:  \(\left\{ {\begin{array}{*{20}{l}}{U = {U_1} + {U_2}}\\{I = {I_1} = {I_2}}\end{array}} \right.\)

Công thức của mạch mắc song song: \(\left\{ {\begin{array}{*{20}{l}}{U = {U_1} = {U_2}}\\{I = {I_1} + {I_2}}\end{array}} \right.\)

Lời Giải:

Hiệu điện thế của mạch: \(U = 18V\)

Đèn sáng bình thường thì:  \(\left\{ {\begin{array}{*{20}{l}}{{U_1} = 6V}\\{{U_2} = 6V}\\{{U_3} = 6V}\end{array}} \right.\)

Khi mắc ba bóng đèn mắc nối tiếp với nhau: \(U = {U_1}{\rm{ + }}{U_2}{\rm{ + }}{U_3} = 18V\)

Thật vậy: Khi mắc Đ₁ nối tiếp Đ₂ nối tiếp Đ₃ \( \Rightarrow I = {I_1} = {I_2} = {I_3}\,\,\,(1)\)

Mà \({R_1} = {R_2} = {R_3}\,\,\,(2)\)

Từ (1) và (2) suy ra:

\(\begin{array}{*{20}{l}}{{U_1} = {U_2} = {U_3} \\\Rightarrow U = {U_1} + {U_2} + {U_3} = 3{U_1} = 18V \\\Rightarrow {U_1} = 6V}\\{ \Rightarrow {U_2} = {U_3} = 6V}\end{array}\)

Vậy 3 đèn sáng bình thường.

Chọn D.

Câu 10:

Phương pháp giải:

Điện trở tương đương của mạch điện mắc nối tiếp: \({R_{nt}} = {R_2} + {\rm{ }}{R_2} + {\rm{ }}... + {R_n}\)

Điện trở tương đương của mạch điện mắc song song: \(\frac{1}{{{R_{//}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\)

Lời Giải:

Cấu tạo mạch điện: \(\left[ {{R_4}//\,\left( {{R_1}\,nt\,{R_2}} \right)} \right]\,\,nt\,\left( {{R_3}//{R_5}} \right)\)

Ta có:  \({R_1}\,nt\,{R_2} \Rightarrow {R_{12}} = {R_1} + {R_2} = 2 + 4 = 6{\mkern 1mu} {\mkern 1mu} \left( \Omega  \right)\)

\(\begin{array}{*{20}{l}}{{R_4}//{R_{12}} \Rightarrow {R_{124}} = \frac{{{R_4}.{R_{12}}}}{{{R_4} + {R_{12}}}} = \frac{{6.6}}{{6 + 6}} = 3{\mkern 1mu} {\mkern 1mu} \left( \Omega  \right)}\\{{R_3}//{R_5} \Rightarrow {R_{35}} = \frac{{{R_3}.{R_5}}}{{{R_3} + {R_5}}} = \frac{{2.2}}{{2 + 2}} = 1{\mkern 1mu} {\mkern 1mu} \left( \Omega  \right)}\\{{R_{124}}nt{R_{35}} \Rightarrow {R_{td}} = {R_{124}} + {R_{35}} = 3 + 1 = 4{\mkern 1mu} {\mkern 1mu} \left( \Omega  \right)}\end{array}\)

Chọn C.

Câu 11:

Phương pháp giải:

Công thức tính điện trở của đoạn mạch nối tiếp và song song: \(\left\{ {\begin{array}{*{20}{l}}{{R_{nt}} = {R_1} + {R_2}}\\{{R_{//}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}}\end{array}} \right.\)

Lời Giải:

Đoạn mạch gồm: \({R_1}{\mkern 1mu} {\mkern 1mu} nt{\mkern 1mu} {\mkern 1mu} \left( {{R_2}//{R_x}} \right)\)

Điện trở tương đương của đoạn mạch:

\(\begin{array}{*{20}{l}}{{R_{AB}}\; = {R_1}\; + {R_{2x}}\; \Leftrightarrow {R_1} + \frac{{{R_2}{R_x}}}{{{R_2} + {R_x}}} = {R_{AB}}}\\{ \Leftrightarrow 7 + \frac{{12.{R_x}}}{{12 + {R_x}}} = 10 \Leftrightarrow \frac{{12.{R_x}}}{{12 + {R_x}}} = 3}\\{ \Leftrightarrow 12.{R_x} = 3.\left( {12 + {R_x}} \right)\\ \Leftrightarrow 9.{R_x} = 36 \Rightarrow {R_x} = 4\Omega }\end{array}\)

Chọn C.

Câu 12:

Phương pháp giải:

Điện trở của dây dẫn tỉ lệ thuận với chiều dài \(l\) của dây dẫn, tỉ lệ nghịch với tiết diện S của dây dẫn và phụ thuộc vào vật liệu làm dây dẫn: \(R = \frac{{\rho l}}{S}\)

Lời Giải:

Ta có: \(R = \frac{{\rho l}}{S} \Rightarrow R \in \rho ,l,S\)

\( \Rightarrow \) Điện trở của dây dẫn không phụ thuộc vào khối lượng của dây dẫn

Chọn B.

Câu 13:

Phương pháp giải:

Điện trở của dây dẫn tỉ lệ thuận với chiều dài \(l\) của dây dẫn, tỉ lệ nghịch với tiết diện S của dây dẫn và phụ thuộc vào vật liệu làm dây dẫn: \(R = \frac{{\rho l}}{S}\)

Lời Giải:

Ban đầu chiều dài của dây dẫn là \(l \Rightarrow R = \frac{{\rho l}}{S}\)

Sau đó cắt đoạn dây thành 4 đoạn có chiều dài bằng nhau thì chiều dài của dây dẫn sau đó là:

\(l' = \frac{l}{4} \Rightarrow R' = \frac{{\rho \frac{l}{4}}}{S} = \frac{R}{4} = 0,25R\)

Chọn A.

Câu 14:

Phương pháp giải:

Công thức tính điện trở:  \(R = \frac{{\rho l}}{S}\)

Định luật Ôm:  \(I = \frac{U}{R}\)

Đèn sáng mạnh lên khi cường độ dòng điện chạy qua đèn tăng và ngược lại.

Lời Giải:

Mạch gồm: \({R_b}\,nt\,{R_D}\)

Điện trở của biến trở: \({R_b} = \frac{{\rho l}}{S}\)

Chiều dòng điện đi từ cực (+) qua dây dẫn, thiết bị điện rồi về cực (-) của nguồn điện. Khi con chạy tiến dần về đầu N chiều dài của biến trở tăng dần làm cho điện trở của dây dẫn tăng dần, kéo theo điện trở tương đương của toàn mạch tăng dần.

Cường độ dòng điện chạy qua đèn là: \({I_D} = {I_b} = \frac{U}{{{R_b}{\mkern 1mu}  + {R_D}}}\)

U không đổi, điện trở tương đương của toàn mạch tăng thì số chỉ của ampe kế sẽ giảm dần đi.

Chọn A.

Câu 15:

Phương pháp giải:

+ Điện trở của dây dẫn: \(R = \frac{{\rho l}}{S}\)

+ Định luật Ôm: \(I = \frac{U}{R}\)

+ Đèn sáng mạnh hơn khi cường độ dòng điện chạy qua đèn tăng.

Lời Giải:

Mạch điện gồm: Đèn nối tiếp với biến trở nên: \({I_D} = {I_b}\)

\( \Rightarrow \)  Khi cường độ dòng điện chạy qua biến trở tăng thì cường độ dòng điện qua đèn cũng tăng và đèn sáng mạnh hơn.

Mà  \({I_b} \uparrow  \Leftrightarrow {R_b} \downarrow \)

Lại có: \({R_b} = \frac{{\rho l}}{S} \Rightarrow {R_b} \downarrow  \Leftrightarrow l \downarrow \)

\( \Rightarrow \)  Dịch chuyển con chạy C về phía M.

Chọn B.

Câu 16:

Phương pháp giải:

Biến trở là điện trở có thể thay đổi trị số và có thể được sử dụng để điều chỉnh cường độ dòng điện trong mạch.

Lời Giải:

Biến trở có thể thay đổi trị số và có thể sử dụng để điều chỉnh cường độ dòng điện trong mạch.

Chọn D.

Câu 17:

Phương pháp giải:

+ Phát biểu định luật: Nhiệt lượng toả ra ở dây dẫn khi có dòng điện chạy qua tỉ lệ thuận với bình phương cường độ dòng điện, với điện trở của dây dẫn và thời gian dòng điện chạy qua.

+ Hệ thức của định luật Jun-Lenxo: \(Q = {I^2}.R.t\)

Lời Giải:

Hệ thức của định luật Jun-Lenxo: \(Q = {I^2}.R.t\) 

Chọn B.

Câu 18:

Phương pháp giải:

Các biện pháp sử dụng tiết kiệm điện năng:

+ Cần lựa chọn sử dụng các dụng cụ và thiết bị điện có công suất phù hợp.

+ Chỉ sử dụng các dụng cụ và thiết bị điện trong thời gian cần thiết.

Lời Giải:

Biện pháp tiết kiệm hợp lí là: Chỉ đun nấu bằng điện và sử dụng các thiết bị nung nóng khác như bàn là, máy sấy tóc,... trong thời gian tối thiểu cần thiết.

Chọn D.

Câu 19:

Đơn vị của công suất điện là Oát (W)

Chọn B.

Câu 20:

Phương pháp giải:

Điện năng tiêu thụ: \(A = P.t{\mkern 1mu} {\mkern 1mu} \left( {kWh} \right)\)

Lời Giải:

Điện năng tiêu thụ của cả hai thiết bị trong 30 ngày là:

\(A = {P_1}.{t_1} + {P_2}{\mkern 1mu} {t_2} = 100.5.30 + 1000.2.30 \\= 75000{\mkern 1mu} \left( {Wh} \right) = 75\left( {kWh} \right)\)

Tiền điện phải trả:  \(T = 75.2000 = 150\,000\;\) (đồng)

Chọn A.

Câu 21:

Phương pháp giải:

Công suất: \(P = U.I \Rightarrow I = \frac{P}{U}\)

Công thức tính điện năng tiêu thụ: \(A = P.t\)

Công thức tính nhiệt lượng nước thu vào: \(Q = m.c.\Delta t\)

Nhiệt lượng hao phí rất nhỏ thì: \(A = Q\)

Lời Giải:

\(\begin{array}{*{20}{l}}{{U_{dm}} = 220V;{P_{dm}} = 1100W;U = 220V}\\{a)\,\,I = ?}\\{b)\,\,m = 10kg;{t_1} = {{20}^0}C,{t_2} = {{100}^0}C;\\c = 4200J/kg.K;t = ?}\\{c)\,\,t' = 30h;1000d/kW.h;T = ?}\end{array}\)

a)

Vì bình nóng lạnh được sử dụng với hiệu điện thế bằng hiệu điện thế định mức nên công suất tiêu thụ của bình nóng lạnh bằng công suất định mức: \(P = 1100W\)

Cường độ dòng điện qua bình: \(I = \frac{P}{U} = \frac{{1100}}{{220}} = 5A\)

b)

Nhiệt lượng cần thiết để đun sôi 10 lít nước từ \({20^0}C\)  là:

\(Q = m.c.\left( {{t_2} - {t_1}} \right) = 10.4200.\left( {100 - 20} \right) \\= 3,{36.10^6}J\)

Vì nhiệt lượng bị hao phí là rất nhỏ nên nhiệt lượng Q để đun sôi nước sẽ chính bằng lượng điện năng A mà ấm đã tiêu thụ. Ta có:

\(A = Q \Leftrightarrow P.t = Q\\ \Leftrightarrow 1100.t = 3,{36.10^6} \Rightarrow t \approx 51'\)

c)

Điện năng tiêu thụ của bình trong một tháng là:

\(\;A = P.t' = 1,1kW.30h = 33kW.h\)

Tiền phải trả:  \(T = 33.3500 = 115\,\,500d\)

Câu 22:

Phương pháp giải:

a)

+ Điện trở tương đương của đoạn mạch có các điện trở mắc song song:  \(\frac{1}{{{R_{ss}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)

+ Điện trở tương đương của đoạn mạch có các điện trở mắc nối tiếp:  \({R_{nt}} = {R_1} + {R_2}\)

b)

+ Sử dụng biểu thức định luật Ôm: \(I = \frac{U}{R}\)

+ So sánh hiệu điện thế định mức của đèn và hiệu điện thế qua đèn

c)

+ Điện trở tương đương của đoạn mạch có các điện trở mắc nối tiếp: \({R_{nt}} = {R_1} + {R_2}\)

+ Sử dụng biểu thức định luật Ôm:  \(I = \frac{U}{R}\)

+ So sánh hiệu điện thế định mức của đèn và hiệu điện thế qua đèn

Lời Giải:

 

a)

Mạch AB của ta gồm \({R_1}\,nt\,\left( {{R_2}//{R_D}} \right)\)

Ta có: \({R_{2D}} = \frac{{{R_2}{R_D}}}{{{R_2} + {R_D}}} = \frac{{6.6}}{{6 + 6}} = 3\Omega \)

Điện trở tương đương của đoạn mạch AB: \(R = {R_1} + {R_{2D}} = 3 + 3 = 6\Omega \)

b)

+ Cường độ dòng điện của mạch: \(I = \frac{{{U_{AB}}}}{R} = \frac{{12}}{6} = 2A\)

Số chỉ của ampe kế chính là cường độ dòng điện trong mạch  2A

+ Hiệu điện thế  \({U_{2D}} = {U_2} = {\rm{ }}{U_D}\)

Ta có: \({U_{2D}} = I.{R_{2D}} = 2.3 = 6V \Rightarrow {U_D} = 6V\)

Nhận thấy  \({U_D} = {U_{dm}} = 6V \Rightarrow \) Đèn sáng bình thường

c)

Khi tháo bỏ \({R_2}\), mạch của ta gồm \({R_1}\,nt\,{R_D}\)

Cường độ dòng điện qua mạch lúc này: \(I' = \frac{{{U_{AB}}}}{{R'}} = \frac{{{U_{AB}}}}{{{R_1} + {R_D}}} = \frac{{12}}{{3 + 6}} = \frac{4}{3}A\)

+ Hiệu điện thế qua đèn khi đó:  \({U_D} = I'.{R_D} = \frac{4}{3}6 = 8V > {U_{dm}}\)

\( \Rightarrow \) Đèn sáng mạnh dễ cháy.

Câu 23:

Phương pháp giải:

Công thức tính điện trở của mạch nối tiếp và song song: \(\left\{ {\begin{array}{*{20}{l}}{{R_{nt}} = {R_1} + {R_2}}\\{{R_{//}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}}\end{array}} \right.\)

Cường độ dòng điện chạy trong mạch: \(I = \frac{U}{{{R_{td}}}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{I_{\max }} \Leftrightarrow {R_{td\min }}}\\{{I_{\min }} \Leftrightarrow {R_{td\max }}}\end{array}} \right.\)

Lời Giải:

Tóm tắt:

\(\begin{array}{*{20}{l}}{{R_{bmax}}\; = 30\Omega ;{R_1}\; = 15\Omega ;{R_2}\; = 10\Omega ;U = 4,5V}\\{{I_{1max}}\; = ?;{I_{1min}}\; = ?}\end{array}\)

Giải:

 

Mạch điện gồm \({R_1}{\mkern 1mu} nt{\mkern 1mu} \left( {{R_2}//{R_b}} \right)\)

Điện trở tương đương của cụm đoạn mạch \(\left( {{R_2}\;//{\rm{ }}{R_b}} \right)\)  là:  \({R_{2b}}{\mkern 1mu}  = \frac{{{R_2}{R_b}}}{{{R_2} + {R_b}}}\)

Điện trở tương đương toàn mạch: \({R_{td}}\; = {R_1}\; + {R_{2b}} = {R_1} + \frac{{{R_2}{R_b}}}{{{R_2} + {R_b}}}\)

Cường độ dòng điện chạy qua \({R_1}\) : \({I_1} = I = \frac{U}{{{R_{td}}\;}} = \frac{U}{{{R_1} + \frac{{{R_2}{R_b}}}{{{R_2} + {R_b}}}}}\)

+ Để \({I_{1\max }} \Leftrightarrow {R_{td\min }} \Leftrightarrow {R_{2b\min }} \Leftrightarrow {R_{b\min }} = 0 \\\Rightarrow {I_{1\max }} = \frac{U}{{{R_1}}} = \frac{{4,5}}{{15}} = 0,3A\)

+ Để  \({I_{1\min }} \Leftrightarrow {R_{td\max }} \Leftrightarrow {R_{2b\max }} \Leftrightarrow {R_{b\max }} = 30\Omega \)

\(\begin{array}{*{20}{l}}{ \Rightarrow {R_{2b}}{\mkern 1mu}  = \frac{{{R_2}{R_{b\max }}}}{{{R_2} + {R_{b\max }}}} = \frac{{10.30}}{{10 + 30}} = 7,5\Omega }\\{ \Rightarrow {I_{1\min }} = \frac{U}{{{R_1} + {R_{2b}}}} = \frac{{4,5}}{{15 + 7,5}} = 0,2A}\end{array}\).

HocTot.Nam.Name.Vn