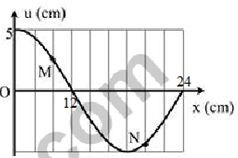
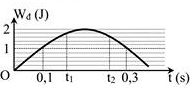
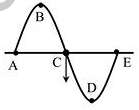
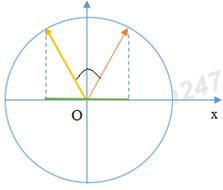
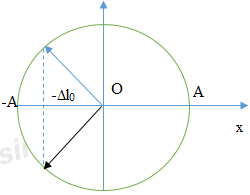
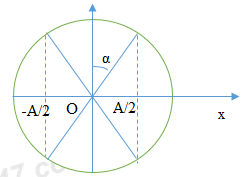
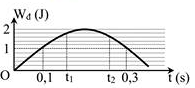
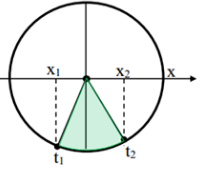
Đề kiểm tra giữa học kì 1 Vật lí 12 - Đề số 05 có lời giải chi tiếtĐề kiểm tra giữa kì 1 vật lí 12 - Đề số 05 được biên soạn theo hình thức trắc nghiệm có lời giải chi tiết giúp các em ôn tập hiệu quả chuẩn bị cho bài kiểm tra trên lớp Đề bài Câu 1: Một con lắc lò xo gồm vật nhỏ khối lượng m và lò xo có độ cứng k. Con lắc dao động điều hòa với tần số góc là A. \(2\pi \sqrt {\frac{m}{k}} \) B. \(2\pi \sqrt {\frac{k}{m}} \) C. \(\sqrt {\frac{m}{k}} \) D. \(\sqrt {\frac{k}{m}} \) Câu 2: Một vật dao động điều hòa theo phương trình \(x = 5.\cos \left( {\frac{{3\pi }}{4}t + \frac{\pi }{4}} \right)\) cm. Pha ban đầu của dao động là A. \(\pi \) B. \(\frac{{3\pi }}{4}\) C. \(\frac{\pi }{2}\) D. \(\frac{\pi }{4}\) Câu 3: Tại một nơi trên Trái Đất có gia tốc tơi tự do g, một con lắc đơn mà dây treo dài l đang dao động điều hòa. Tần số dao động của con lắc là A. \(\sqrt {\frac{g}{l}} \) B. \(2\pi \sqrt {\frac{g}{l}} \) C. \(2\pi \sqrt {\frac{l}{g}} \) D. \(\frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \) Câu 4: Khi nói về dao động cơ cưỡng bức, phát biểu nào sau đây đúng? A. Dao động cưỡng bức có tần số luôn bằng tần số riêng của hệ dao động B. Biên độ của dao động cưỡng bức càng lớn nếu tần số của lực cưỡng bức càng lớn C. Biên độ của dao động cưỡng bức càng lớn nếu chu kì của lực cưỡng bức càng lớn D. Dao động cưỡng bức có chu kì luôn bằng chu kì của lực cưỡng bức. Câu 5: Hai dao động điều hòa, cùng phương, cùng tần số, ngược pha, có biên độ lần lượt là A1, A2. Biên độ dao động tổng hợp của hai dao động này là A. \(\left| {{A_1} - {A_2}} \right|\) B. \({A_1} + {A_2}\) C. \(\sqrt {\left| {A_1^2 - A_2^2} \right|} \) D. \(\sqrt {A_1^2 + A_2^2} \) Câu 6: Phát biểu nào sau đây sai khi nói về sóng cơ? A. Tốc độ truyền sóng là tốc độ lan truyền dao động trong môi trường B. Tốc độ truyền sóng tỉ lệ nghịch với chu kì của sóng C. Hai phần tử cách nhau một bước sóng trên cùng một phương truyền sóng thì dao động đồng pha với nhau D. Bước sóng là quãng đường mà sóng truyền được trong một chu kì. Câu 7: Nếu biên độ dao động của một vật dao động điều hòa giảm hai lần thì tần số dao động của vật A. Tăng 4 lần B. không đổi C. giảm 2 lần D. tăng 2 lần Câu 8: Phát biểu nào sau đây là đúng khi nói về sóng cơ học A. Sóng dọc và sóng ngang đều truyền được trong chất rắn B. Sóng dọc không truyền dược trong chất lỏng và trong chân không C. Sóng dọc là sóng truyền theo phương thẳng đứng, còn sóng ngang truyền theo phương ngang D. Khi sóng truyền đi, các phân tử vật chất nơi sóng truyền qua cùng truyền đi theo sóng Câu 9: Hai chất điểm M1 và M2 cùng dao động điều hòa trên một trục Ox, quanh điểm O với cùng tần số f có phương trình là: \({x_1} = A\cos \left( {2\pi ft - \frac{\pi }{3}} \right);{x_2} = 2A.\cos \left( {2\pi ft + \frac{{2\pi }}{3}} \right)\) . Độ dài đại số M1M2 = x biến đổi theo thời gian với quy luật nào? A. \(x = A.\cos \left( {2\pi ft + \frac{{2\pi }}{3}} \right)\) B. \(x = 3A.\cos \left( {2\pi ft + \frac{{2\pi }}{3}} \right)\) C. \(x = A.\cos \left( {2\pi ft + \frac{\pi }{3}} \right)\) D. \(x = 3A.\cos \left( {2\pi ft + \frac{\pi }{3}} \right)\) Câu 10: Khi nói về dao động điều hòa của một vật, phát biểu nào sau đây là sai? A. Chuyển động của vật từ vị trí cân bằng ra vị trí biên là chuyển động chậm dần đều B. Lực kéo về luôn hướng về vị trí cân bằng C. Vecto gia tốc của vật luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lớn của li độ D. Vecto vận tốc của vật đổi chiều tại các vị trí biên. Câu 11: Một sóng hình sin có tần số f, lan truyền với tốc độ v. Khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng mà các phần tử môi trường tại hai điểm đó dao động ngược pha nhau là A. \(\frac{v}{f}\) B. \(\frac{v}{{2f}}\) C. \(\frac{{vf}}{2}\) D. \(vf\) Câu 12: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với biên độ A, độ dãn của lò xo ở vị trí cân bằng là ∆l0. Nếu ∆l0 > A thì trong quá trình dao động tỉ số giữa độ lớn lực đàn hồi cực đại và cực tiểu là A. \(\frac{{\Delta {l_0} + A}}{{\Delta {l_0} - A}}\) B. \(\frac{{\Delta {l_0} + A}}{A}\) C. \(\frac{A}{{\Delta {l_0} - A}}\) D. \(\frac{A}{{\Delta {l_0}}}\) Câu 13: Vật dao động điều hòa theo phương trình \(x = A.\cos \left( {\frac{{2\pi }}{T}t + \frac{\pi }{2}} \right)\) , gia tốc của vật có độ lớn cực đại tại thời điểm A. \(t = 0,5T\) B. \(t = 0\) C. \(t = T\) D. \(t = 0,25T\) Câu 14: Một vật nhỏ dao động điều hòa trên trục Ox với biên độ A, mốc thế năng tại vị trí cân bằng. Vật có động năng bằng thế năng khi cách vị trí cân bằng một khoảng A. \(\frac{A}{4}\) B. \(\frac{{A\sqrt 3 }}{2}\) C. \(\frac{A}{2}\) D. \(\frac{{A\sqrt 2 }}{2}\) Câu 15: Để số dao động trong một giây của con lắc đơn dao động điều hòa tăng lên thì phải A. Giảm chiều dài sợi dây B. Tăng chiều dài sợi dây C. Giảm khối lượng vật nặng D. Tăng khối lượng vật nặng Câu 16: Ở một nơi trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa với cùng biên độ. Gọi l1, F1 và l2, F2 lần lượt là chiều dài, độ lớn lực kéo về cực đại của con lắc thứ nhất và của con lắc thứ hai. Biết 4l1 = 5l2. Tỉ số \(\frac{{{F_1}}}{{{F_2}}}\) bằng A. \(\frac{5}{4}\) B. \(\frac{4}{5}\) C. \(\frac{{25}}{{16}}\) D. \(\frac{{16}}{{25}}\) Câu 17: Sóng cơ truyền dọc theo trục Ox có phương trình là \(u = 4\cos \left( {5\pi t - 0,2\pi x} \right)\) cm với t đo bằng s, x đo bằng m. Tốc độ truyền sóng này là A. 4 m/s B. 25 cm/s C. 25 m/s D. 4 cm/s Câu 18: Có hệ con lắc lò xo treo thẳng đứng và hệ con lắc đơn cùng dao động điều hòa tại một nơi nhất đinh. Chu kì dao động của chúng bằng nhau, nếu chiều dài của con lắc đơn A. Bằng độ biến dạng của lò xo ở vị trí thấp nhất B. Bằng chiều dài của lò xo khi vật ở vị trí cân bằng C. Bằng độ biến dạng của lò xo khi vật ở vị trí cân bằng D. Bằng chiều dài tự nhiên của lò xo Câu 19: Cho các phát biểu sau. Số phát biểu đúng là - Cơ năng của con lắc lò xo tỉ lệ thuận với biên độ dao động - Khi con lắc lò xo dao động điều hòa, gia tốc sớm pha \(\frac{\pi }{2}\) so với vận tốc - Khi con lắc lò xo dao động điều hòa, gia tốc và vận tốc luôn cùng tần số với li độ - Khi tăng độ cứng của lò xo thì tần số dao động của con lắc tăng Với con lắc lò xo thẳng đứng dao động điều hòa, lực kéo về là lực đàn hồi của lò xo A. 5 B. 4 C. 3 D. 2 Câu 20: Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ, đang dao động điều hòa trên mặt phẳng nằm ngang. Động năng của con lắc đạt giá trị cực đại khi A. Gia tốc có độ lớn bằng không B. Lò xo có chiều dài cực tiểu C. Lực hồi phục có độ lớn cực đại D. Lò xo có chiều dài cực đại Câu 21: Một sóng cơ học lan truyền trên một phương truyền sóng với vận tốc 3 m/s. Phương trình sóng của một điểm O trên phương truyền đó là \({u_O} = 2\cos \left( {4\pi t} \right)(cm)\) . Phương trình sóng tại điểm M nằm sau O và cách O một khoảng 50 cm là A. \({u_M} = 2\cos \left( {4\pi t - \frac{{2\pi }}{3}} \right)cm\) B. \({u_M} = 2\cos \left( {4\pi t - \frac{\pi }{3}} \right)cm\) C. \({u_M} = 2\cos \left( {4\pi t + \frac{{2\pi }}{3}} \right)cm\) D. \({u_M} = 2\cos \left( {4\pi t + \frac{\pi }{3}} \right)cm\) Câu 22: Một xe máy chạy trên con đường lát gạch, cứ cách khoảng 12m trên đường lại có một rãnh nhỏ. Chu kì dao động riêng của khung xe trên các lò xo giảm xóc là 1,5 s. Xe bị xóc mạnh nhất khi vận tốc của xe là A. 27 km/h B. 64,8 km/h C. 28,8 km/s D. 60 km/h Câu 23: Một con lắc lò xo dao động tắt dần trên mặt phẳng nằm ngang. Cứ sau mỗi chu kì biên độ giảm 3%. Gốc thế năng tại vị trí của vật mà lò xo không biến dạng. Phần trăm cơ năng của con lắc bị mất đi sau một dao động toàn phần là A. 1,73% B. 1,51 % C. 5,91 % D. 9,41 % Câu 24: Một con lắc lò xo nằm ngang có tần số góc dao động riêng ω0 = 20 rad/s. Tác dụng vào vật nặng theo phương của trục lò xo một ngoại lực biến thiên điều hòa \({F_n} = {F_0}.\cos 10t\left( N \right)\). Sau một thời gian vật dao động điều hòa với biên độ 6 cm. Khi vật qua li độ x = 3,6 cm thì tốc độ của vật là A. 36 cm/s B. 72 cm/s C. 48 cm/s D. 96 cm/s Câu 25: Một vật dao động điều hòa phải mất 0,2 s để đi từ điểm có vận tốc bằng không tới điểm tiếp theo cũng có vận tốc bằng không, hai điểm ấy cách nhau 6cm. Phát biểu nào sau đây sai? A. Chu kì dao động là 0,4 s. B. Tốc độ trung bình trong một chu kì là 0,6 m/s C. Vận tốc cực đại của vật là 0,15π m/s D. Quãng đường đi được trong một chu kì là 12 cm Câu 26: Đồ thị biểu diễn dao động điều hòa ở hình vẽ bên ứng với phương trình vận tốc nào sau đây?
A. \(v = 100\pi \cos \left( {20\pi t} \right)cm/s\) B. \(v = 50\pi \cos \left( {10\pi t} \right)cm/s\) C. \(v = 100\pi \cos \left( {20\pi t + \pi } \right)cm/s\) D. \(v = 50\pi \cos \left( {10\pi t + \pi } \right)cm/s\) Câu 27: Một con lắc lò xo gồm lò xo nhẹ có độ cứng k và vật nhỏ có khối lượng m dao động điều hòa theo phương nằm ngang. Lấy π2 = 10. Khi vật ở vị trí có li độ x thì vận tốc của vật là v. Lực hồi phục cực đại của con lắc được xác định theo biểu thức A. \(k\left( {{x^2} + \frac{{m{v^2}}}{k}} \right)\) B. \(k\sqrt {\left( {{x^2} + \frac{{k{v^2}}}{m}} \right)} \) C. \(k\sqrt {\left( {{x^2} + \frac{{m{v^2}}}{k}} \right)} \) D. \(k\left( {{x^2} + \frac{{k{v^2}}}{m}} \right)\) Câu 28: Một con lắc đơn có chiều dài dây treo 50 cm, dao động điều hòa tại nơi có gia tốc trọng trường 9,8 m/s2. Kéo con lắc sao cho dây treo hợp với phương thẳng đứng góc 100 rồi thả nhẹ cho con lắc dao động điều hòa. Con lắc dao động với vận tốc cực đại là A. 22,1 cm/s B. 22,1 m/s C. 38,6 cm/s D. 3,86 m/s Câu 29: Một vật thực hiện đồng thời hai dao động điều hòa có phương trình \({x_1} = 7\cos \left( {\omega t + \frac{\pi }{{12}}} \right)cm;\) \({x_2} = {A_2}\cos \left( {\omega t + \frac{{7\pi }}{{12}}} \right)cm\) . Biết vận tốc cực đại của vật là 1 m/s và gia tốc cực đại của vật là 4 m/s2. Khi đó biên độ A2 là A. 24 cm B. 18 cm C. 12 cm D. 9 cm Câu 30: Một sóng cơ lan truyền trên sợi dây dài với biên độ không đổi. Điều kiện để tốc độ trung bình trong một chu kì của một điểm trên sợi dây bằng một nửa tốc độ truyền sóng là A. Bước sóng bằng hai lần biên độ sóng B. Bước sóng bằng một nửa biên độ sóng C. Bước sóng bằng tám lần biên độ sóng D. Bước sóng bằng bốn lần biên độ sóng Câu 31: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với chu kì 0,2 s. Biết trong mỗi chu kì dao động, thời gian lò xo bị giãn lớn gấp 3 lần thời gian lò xo bị nén. Lấy g = 10 m/s2. Biết khối lượng vật nặng là 200g, cơ năng của con lắc là A. 0,04 J B. 0,06 J C. 0,02 J D. 0,03 J Câu 32: Một sóng ngang truyền trên mặt nước với tần số f = 5Hz. Tại một thời điểm nào đó một phần mặt cắt của nước có hình dạng như hình vẽ. Trong đó khoảng cách từ vị trí cân bằng của A đến vị trí cân bằng của C là 40 cm và điểm C đang đi xuống qua vị trí cân bằng. Phát biểu nào sau đây sai?
A. Tốc độ truyền sóng là 4 m/s. B. Sóng truyền từ A đến E. C. A và C luôn dao động ngược pha. D. B và C luôn dao động vuông pha. Câu 33: Một vật dao động điều hòa quang vị trí cân bằng O. Tại thời điểm t1, vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t1 đến thời điểm t2 = t1 + 0,5 s vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong khoảng thời gian từ thời điểm t2 đến thời điểm t3 = t2 + 1,5s, vật đi được quãng đường 20 cm. Trong quá trình dao động, quãng đường lớn nhất vật đi được trong 5s là A. 67 cm B. 70 cm C. 75 cm D. 77 cm Câu 34: Tiến hành thí nghiệm đo gia tốc trọng trường bằng con lắc đơn, một học sinh đo được chiều dài con lắc là (80,0 ± 0,1) cm. Chu kì dao động của nó là (1,80 ± 0,02) s. Lấy π2 = 9,87 và bỏ qua sai số của số π. Gia tốc trọng trường do học sinh đo được tại nơi làm thí nghiệm là A. \(g = {(9,77 \pm 0,23)_{}}(m/{s^2})\) B. \(g = {(9,75 \pm 0,14)_{}}(m/{s^2})\) C. \(g = {(9,77 \pm 0,14)_{}}(m/{s^2})\) D. \(g = {(9,75 \pm 0,23)_{}}(m/{s^2})\) Câu 35: Một con lắc lò treo thẳng đứng gồm lò xo độ cứng k = 100 N/m, quả nặng khối lượng 400g. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chọn mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là 0,16 J. Lấy gia tốc rơi tự do g = 10 m/s2 và π2 = 10. Trong một chu kì, khoảng thời gian mà lực đàn hồi tác dụng lên vật nặng có chiều hướng từ trên xuống dưới là A. 0,1 s B. \(\frac{2}{{15}}s\) C. 0,3 s D. \(\frac{4}{{15}}s\) Câu 36: Hai chất điểm M và N có cùng khối lượng, dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biên độ của M là 8 cm, của N là 15 cm. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 17 cm. Mốc thế năng tại vị trí cân bằng. Ở thời điểm mà M có động năng bằng ba lần thế năng, tỉ số động năng của M và động năng của N là A. \(\frac{{16}}{{75}}\) B. \(\frac{{64}}{{225}}\) C. \(\frac{{16}}{{225}}\) D. \(\frac{{64}}{{75}}\) Câu 37: Một sóng ngang hình sin truyền trên một sợi dây dài. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác đinh. Trong quá trình lan truyền sóng, khoảng cách lớn nhất giữa hai phần tử M và N là
A. 13,90 cm B. 15, 81 cm C. 18,02 cm D. 17,84 cm Câu 38: Một con lắc lò xo dao động điều hòa theo phương trình x = 4cos(ωt) cm. Trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có động năng không vượt quá ba lần thế năng là 2s. Lấy π2 = 10. Thời điểm để con lắc đi qua vị trí x = 2 cm theo chiều dương lần thứ 2018 là A. 12103 s B. \(\frac{{12103}}{2}s\) C. 12107 s D. \(\frac{{12107}}{2}s\) Câu 39: Một con lắc lò xo dao động điều hòa với tần số 5 Hz. Biết rằng tại thời điểm ban đầu vật bắt đầu dao động tại vị trí mà lò xo có chiều dài lớn nhất. Tỉ số giữa tốc độ trung bình và độ lớn vận tốc trung bình của vật sau thời gian \(\frac{1}{3}s\) kể từ lúc vật bắt đầu dao động có giá trị gần nhất với giá trị nào sau đây? A. 4 B. 3 C. 2 D. 5 Câu 40: Một con lắc lò xo đang dao động điều hòa. Hình bên là đồ thị biểu diễn sự phụ thuộc của động năng Wđ của con lắc theo thời gian t. Phát biểu nào sau đây không đúng?
A. \({t_2} - {t_1} = 0,1s\) B. Tại thời điểm t2 vật chuyển động theo chiều âm C. Tại thời điểm t1 thì động năng bằng 9 lần thế năng D. Chu kì dao động của vật là 0,8s Lời giải chi tiết
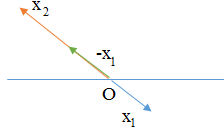
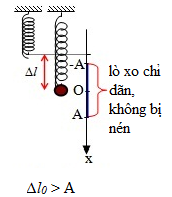
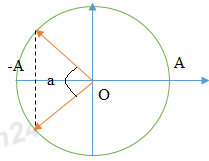
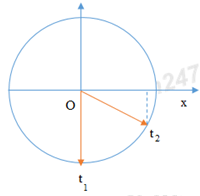
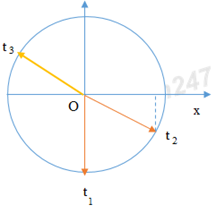
Câu 1: Phương pháp: Sử dụng lí thuyết về dao động điều hòa của con lắc lò xo Cách giải: Tần số góc của dao động của con lắc lò xo là: \(\omega = \sqrt {\frac{k}{m}} \) Chọn D. Câu 2: Phương pháp: Phương trình dao động điều hòa tổng quát là \(x = A\cos \left( {\omega t + \varphi } \right)\) với φ là pha ban đầu. Cách giải: Phương trình dao động:\(x = 5.\cos \left( {\frac{{3\pi }}{4}t + \frac{\pi }{4}} \right)\) cm Pha ban đầu của dao động là \(\frac{\pi }{4}\,\,rad\) Chọn D. Câu 3: Phương pháp Sử dụng lý thuyết dao động của con lắc đơn. Cách giải: Tần số của dao động con lắc đơn là: \(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \) Chọn D. Câu 4: Phương pháp: Sử dụng lý thuyết về đặc điểm của dao động cưỡng bức. Cách giải: Đặc điểm của dao động cưỡng bức: + Dao động cưỡng bức có biên độ không đổi và có tần số bằng tần số của lực cưỡng bức. + Biên độ của dao động cưỡng bức không chỉ phụ thuộc vào biên độ của lực cưỡng bức mà còn phụ thuộc cả và độ chênh lệch giữa tần số của lực cưỡng bức và tần số riêng của hệ dao động. Khi tần số của lực cưỡng bức càng gần tần số riêng thì beien độ dao động cưỡng bức càng lớn. Ngoài ra, lực cản của môi trường cũng ảnh hưởng đến biên độ của lực cưỡng bức. Chọn D. Câu 5: Phương pháp: Biên độ dao động tổng hợp của hai dao động điều hòa được xác định bởi: \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \Delta \varphi } \) Cách giải: Biên độ dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số, ngược pha là: \(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \Delta \varphi } \\= \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \pi } \\ \Leftrightarrow A = \sqrt {A_1^2 + A_2^2 - 2{A_1}{A_2}} \\ = \sqrt {{{\left( {{A_1} - {A_2}} \right)}^2}} = \left| {{A_1} - {A_2}} \right|\end{array}\) Chọn A. Câu 6: Phương pháp: Lí thuyết về sóng cơ Cách giải: Ta có: + Sóng cơ là dao động cơ lan truyền trong môi trường. + Tốc độ truyền sóng là tốc độ lan truyền dao động trong môi trường. Tốc độ truyền sóng phụ thuộc vào đặc điểm môi trường. Đối với mỗi môi trường, tốc độ truyền sóng v có một giá trị không đổi. + Bước sóng là quãng đường mà sóng truyền được trong một chu kì, \(\lambda = v.T = \frac{v}{f}\) . + Hai phần tử cách nhau một số nguyên lần bước sóng cùng nằm trên một phương truyền sóng thì dao động cùng pha với nhau. Vậy đáp án B sai. Chọn B. Câu 7: Phương pháp: Công thức tính tần số dao động điều hòa: \(f = \frac{\omega }{{2\omega }} = \frac{1}{T}\) Cách giải: Tần số dao động điều hòa là: \(f = \frac{\omega }{{2\omega }} = \frac{1}{T}\) Vậy tần số dao động không phụ thuộc vào biên độ sóng. Chọn B. Câu 8: Phương pháp: Sử dụng lý thuyết về sóng cơ học. Cách giải: + Sóng trong đó các phần tử môi trường dao động theo phương vuông góc với phương truyền sóng gọi là sóng ngang. Sóng ngang truyền được trong chất rắn, và trường hợp sóng trên mặt nước. + Sóng trong đó các phần tử môi trường dao động theo phương trùng với phương truyền sóng gọi là sóng dọc. Sóng dọc truyền được trong chất rắn, chất lỏng, chất khí. + Sóng cơ không truyền được trong chân không. + Sóng cơ là dao động cơ lan truyền trong một môi trường. Khi sóng truyền đi, các phân tử vật chất nơi sóng đi qua dao động quanh vị trí cân bằng chứ không truyền đi theo sóng → Vậy sóng dọc và sóng ngang đều truyền được trong chất rắn là đáp án đúng Chọn A. Câu 9: Phương pháp: Áp dụng công thức khoảng cách M1M2 = x = x2 – x1 Sử dụng giản đồ vecto để tìm dao động x bằng phép cộng vecto. Cách giải: Khoảng cách \({M_1}{M_2} = \left| x \right| = \left| {{x_2} - {x_1}} \right| = \left| {{x_2} + \left( { - {x_1}} \right)} \right| \\= \left| {A.\cos \left( {2\pi ft + \frac{{2\pi }}{3}} \right) - A\cos \left( {2\pi ft - \frac{\pi }{3}} \right)} \right|\) Biểu diễn bằng giản đồ vecto ta có:
Sử dụng quy tắc cộng vecto. Vậy \(x = 3A.\cos \left( {2\pi ft + \frac{{2\pi }}{3}} \right)cm\) Chọn B. Câu 10: Phương pháp: Lý thuyết về dao động điều hòa: Trong dao động điều hòa, vận tốc là đại lượng biến thiên điều hòa. Vecto vận tốc đổi chiều tại các vị trí biên. Khi vật đi từ vị trí cân bằng ra biên, vật chuyển động chậm dần. Gia tốc là đại lượng biến thiên điều hòa, vecto gia tốc luôn hướng về vị trí cân bằng. Lực kéo về và lực đưa vật về vị trí cân bằng, nó luôn hướng về vị trí cân bằng. Cách giải: Lý thuyết về dao động điều hòa: Trong dao động điều hòa, vận tốc là đại lượng biến thiên điều hòa. Vecto vận tốc đổi chiều tại các vị trí biên. Khi vật đi từ vị trí cân bằng ra biên, vật chuyển động chậm dần. Gia tốc là đại lượng biến thiên điều hòa, vecto gia tốc luôn hướng về vị trí cân bằng. Lực kéo về và lực đưa vật về vị trí cân bằng, nó luôn hướng về vị trí cân bằng. Vậy, phát biểu A là chưa chính xác. Chọn A. Câu 11: Phương pháp: Bước sóng: \(\lambda = v.T = \frac{v}{f}\) Khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động ngược pha là nửa bước sóng. Cách giải: Khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động ngược pha là nửa bước sóng là: \(d = \frac{\lambda }{2} = \frac{v}{{2f}}\) Chọn B. Câu 12: Phương pháp: Sử dụng công thức tính lực đàn hồi F = k∆l Cách giải: Ta có hình vẽ: Độ lớn lực đàn hồi cực đại là tại biên dương, độ lớn lực đàn hồi cực tiểu là tại biên âm. Ta có tỉ số: \(\frac{{{F_{dh\max }}}}{{{F_{dh\min }}}} = \frac{{k(A + \Delta {l_0})}}{{k(\Delta {l_0} - A)}} = \frac{{\Delta {l_0} + A}}{{\Delta {l_0} - A}}\) Chọn A. Câu 13: Phương pháp: Phương trình gia tốc a = -ω2x. Gia tốc cực đại có giá trị amax = ω2A. Cách giải: Phương trình gia tốc a = -ω2x. Gia tốc cực đại có giá trị là: amax = ω2A \(\begin{array}{l} \Rightarrow x = - A \Leftrightarrow A.\cos \left( {2\pi \frac{t}{T} + \frac{\pi }{2}} \right) \\= \pm A \Rightarrow 2\pi \frac{t}{T} + \frac{\pi }{2} = \pi + k2\pi \\ \Leftrightarrow t = \frac{1}{4}T + kT = 0,25T + kT\end{array}\) Với k là các giá trị nguyên. Khi k = 0 thì t = 0,25T Chọn D. Câu 14: Phương pháp: Áp dụng công thức tính cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \frac{1}{2}k{x^2} + \frac{1}{2}m{v^2} = \frac{1}{2}k{A^2}\) Cách giải: Áp dụng công thức tính cơ năng, ta có: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = 2{W_1}\\ \Rightarrow \frac{1}{2}k{x^2} = \frac{1}{2}\frac{1}{2}k{A^2} \Leftrightarrow x = \frac{A}{{\sqrt 2 }} = A\frac{{\sqrt 2 }}{2}\) Chọn D. Câu 15: Phương pháp: Tần số là số dao động trong một giây. Công thức tính tần số của con lắc đơn:\(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \) Cách giải: Công thức tính tần số của con lắc đơn là:\(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \) Để số dao động trong một giây hay tần số của con lắc đơn dao động điều hòa tăng lên thì giảm chiều dài của con lắc. Chọn A. Câu 16: Phương pháp: Áp dụng công thức tính lực kéo về của con lắc đơn: \({P_t} = - mg\frac{s}{l}\) Cách giải: Áp dụng công thức tính lực kéo về của con lắc đơn là: \({P_t} = - mg\frac{s}{l}\) Ta có: 4l1 = 5l2 \( \Rightarrow \frac{{{F_1}}}{{{F_2}}} = \frac{{{l_2}}}{{{l_1}}} = \frac{4}{5}\) Chọn B. Câu 17: Phương pháp: Phương trình sóng tổng quát: \(u = A.\cos \left( {\omega t + \frac{{2\pi x}}{{v.T}}} \right)\) với v là tốc độ truyền sóng. Cách giải : Sóng cơ truyền dọc theo trục Ox có phương trình: \(u = 4\cos \left( {5\pi t - 0,2\pi x} \right)\) cm, ta có: \(\left\{ \begin{array}{l}\omega = 5\pi \\\frac{{2\pi }}{{v.T}} = 0,2\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}T = \frac{{2\pi }}{\omega } = \frac{2}{5} = 0,4\\v.T = 10\end{array} \right. \\\Rightarrow v = \frac{{10}}{T} = {25_{}}m/s\) Chọn C. Câu 18: Phương pháp: Chu kì dao động của con lắc lò xo treo thẳng đứng: \(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \) Chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \) Cách giải: Chu kì dao động của con lắc lò xo treo thẳng đứng là: \(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \) Chu kì dao động của con lắc đơn là: \(T = 2\pi \sqrt {\frac{l}{g}} \) Để hai con lắc có cùng chu kì thì: \(T = 2\pi \sqrt {\frac{l}{g}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \Rightarrow l = \Delta {l_0}\) Chọn C. Câu 19: Phương pháp: Năng lượng của con lắc lò xo: \({\rm{W}} = \frac{1}{2}.k.{A^2}\) Phương trình li độ, vận tốc, gia tốc của vật: \(\left\{ \begin{array}{l}x = A.\cos \left( {\omega t + \varphi } \right)\\v = \omega A.\cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\\a = {\omega ^2}.A.\cos \left( {\omega t + \varphi + \pi } \right)\end{array} \right.\) Tần số dao động của con lắc lò xo: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \) Khi con lắc lò xo được treo thẳng đứng, lực kéo về khác với lực đàn hồi của lò xo (vì khi ở vị trí cân bằng thì lò xo đã dãn một đoạn ∆l) Cách giải: Năng lượng của con lắc lò xo: \({\rm{W}} = \frac{1}{2}.k.{A^2} \Rightarrow {\rm{W}} \sim {A^2}\) Phương trình li độ, vận tốc, gia tốc của vật là: \(\left\{ \begin{array}{l}x = A.\cos \left( {\omega t + \varphi } \right)\\v = \omega A.\cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\\a = {\omega ^2}.A.\cos \left( {\omega t + \varphi + \pi } \right)\end{array} \right.\) Vậy li độ, vận tốc, gia tốc có cùng tần số Tần số dao động của con lắc lò xo \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \) , khi tăng độ cứng của lò xo thì tần số tăng. Khi con lắc lò xo được treo thẳng đứng, lực kéo về khác với lực đàn hồi của lò xo (vì khi ở vị trí cân bằng thì lò xo đã dãn một đoạn ∆l) Vậy, số phải biểu đúng là 3 Chọn C. Câu 20: Phương pháp: Động năng của con lắc lò xo nằm ngang: \({{\rm{W}}_d} = \frac{1}{2}.m{v^2}\) Động năng cực đại khi vận tốc cực đại, tức là vật đi qua vị trí cân bằng, x = 0. Cách giải: Động năng của con lắc lò xo nằm ngang là: \({{\rm{W}}_d} = \frac{1}{2}.m{v^2}\) Động năng cực đại khi vận tốc cực đại, tức là vật đi qua vị trí cân bằng, x = 0. Mà gia tốc \(a = - {\omega ^2}x\) nên khi đó gia tốc bằng 0. Chọn A. Câu 21: Phương pháp: Phương trình sóng tại M nằm sau và cách O một khoảng x là: \({u_M} = A.\cos \left( {\omega t - \frac{{\omega x}}{v}} \right)\) Cách giải: Phương trình sóng tại M nằm sau và cách O một khoảng x là: \({u_M} = 2.\cos \left( {4\pi t - \frac{{4\pi 0,5}}{3}} \right)\\ = 2\cos \left( {4\pi t - \frac{{2\pi }}{3}} \right)cm\) Chọn A. Câu 22: Phương pháp: Hiện tượng cộng hưởng xảy ra khi tần số dao động cưỡng bức bằng tần số dao động riêng của hệ. Cách giải: Hiện tượng cộng hưởng xảy ra khi tần số dao động cưỡng bức bằng tần số dao động riêng của hệ. Chu kì dao động riêng của xe là 1,5 s, vận tốc của xe để xe bị xóc mạnh nhất là: \(v = \frac{s}{T} = \frac{{12}}{{1,5}} = {8_{}}(m/s) = 28,{8_{}}(km/h)\) Chọn C. Câu 23: Phương pháp: Công thức tính năng lượng con lắc: \({\rm{W}} = \frac{1}{2}.k.{A^2}\) Cách giải: Năng lượng của con lắc là: \({\rm{W}} = \frac{1}{2}.k.{A^2}\) Sau mỗi chu kì biên độ giảm 3% tức là còn 97%, vậy năng lượng giảm là: \(\Delta {\rm{W}} = {{\rm{W}}_1} - {{\rm{W}}_2}\\ = \frac{1}{2}k.{A^2} - \frac{1}{2}.k.{(97\% A)^2} \\= 5,91\% .\frac{1}{2}k.{A^2} = 5,91\% {\rm{W}}\) Chọn C. Câu 24: Phương pháp: Áp dụng công thức độc lập với thời gian: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\) Khi vật chịu tác dụng của ngoại lực cưỡng bức thì vật dao động điều hòa với tần số góc là tần số góc của ngoại lực cưỡng bức. Cách giải: Khi vật chịu tác dụng của ngoại lực cưỡng bức thì vật dao động điều hòa với tần số góc là tần số góc của ngoại lực cưỡng bức, hay ω = 10 rad/s. Áp dụng công thức độc lập với thời gian, ta có: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow 3,{6^2} + \frac{{{v^2}}}{{{{10}^2}}} = {6^2}\\ \Rightarrow v = {48_{}}cm/s\) Chọn D. Câu 25: Phương pháp: Vật dao động điều hòa có vận tốc bằng không tại các biên. Thời gian để vật đi từ biên âm đến biên dương hoặc ngược lại là nửa chu kì, quãng đường đi được là 2A. Quãng đường vật đi được trong một chu kì là 4A. Cách giải: Vật dao động điều hòa có vận tốc bằng không tại các biên. Thời gian để vật đi từ biên âm đến biên dương hoặc ngược lại là nửa chu kì, quãng đường đi được là 2A. Theo đề bài ra vật có chu kì T = 0,4 s và biên độ A = 3 cm. Quãng đường vật đi được trong một chu kì là 4A = 12 cm. Vận tốc cực đại là \(v = \frac{{2\pi }}{T}A = \frac{{2\pi }}{{0,4}}.0,03 = 0,15\pi \left( {m/s} \right)\) Tốc độ trung bình trong một chu kì là \(v = \frac{S}{T} = \frac{{0,12}}{{0,4}} = 0,{3_{}}m/s\) Vậy phát biểu sai là B. Chọn B. Câu 26: Phương pháp: Viết phương trình li độ từ đồ thị, sau đó viết phương trình vận tốc. \(\left\{ \begin{array}{l}x = A.\cos \left( {\omega t + \varphi } \right)\\v = \omega A.\cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\end{array} \right.\) Cách giải: Từ đồ thị ta thấy biên độ là A = 5 cm, chu kì T = 0,2s, tại t = 0 thì vật ở vị trí cân bằng, đi theo chiều dương → Pha ban đầu là: \(\varphi = - \frac{\pi }{2}\,\,\left( {rad} \right)\) Phương trình dao động là: \(x = 5.\cos \left( {\frac{{2\pi }}{{0,2}}t - \frac{\pi }{2}} \right)cm = 5\cos \left( {10\pi t - \frac{\pi }{2}} \right)cm\) Vậy phương trình vận tốc là: \(v = 50\pi \cos \left( {10\pi t} \right)cm/s\) Chọn B. Câu 27: Phương pháp: Khi con lắc lò xo dao động theo phương ngang thì lực hồi phục chính là lực đàn hồi. Lực hồi phục: \({F_{hp}} = kx\) Công thức độc lập với thời gian \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\) Cách giải: Khi con lắc lò xo dao động theo phương ngang thì lực hồi phục chính là lực đàn hồi. Lực hồi phục tác dụng lên vệt là: \({F_{hp}} = kx\) Lực hồi phục cực đại là khi x = A. Áp dụng công thức độc lập với thời gian, ta có: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\\ \Rightarrow A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{x^2} + \frac{{m{v^2}}}{k}} \) Vậy \({F_{hp\max }} = k.\sqrt {{x^2} + \frac{{m{v^2}}}{k}} \) Chọn C. Câu 28: Phương pháp: Áp dụng định luật bảo toàn cơ năng. Động năng cực đại bằng thế năng cực đại. \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = {{\rm{W}}_{d\max }} = {{\rm{W}}_{t\max }} \\\Rightarrow \frac{1}{2}mv_{\max }^2 = mgl\left( {1 - \cos {\alpha _0}} \right)\) Cách giải: Áp dụng định luật bảo toàn cơ năng. Động năng cực đại bằng thế năng cực đại. \(\begin{array}{l}{\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = {{\rm{W}}_{d\max }} = {{\rm{W}}_{t\max }}\\ \Rightarrow \frac{1}{2}mv_{\max }^2 = mgl\left( {1 - \cos {\alpha _0}} \right)\\ \Rightarrow {v_{\max }} = \sqrt {2gl\left( {1 - \cos {\alpha _0}} \right)} \\ = \sqrt {2.9,8.0,5.\left( {1 - \cos {{10}^0}} \right)} \\= 0,{386_{}}m/s = 38,6cm/s\end{array}\) Chọn C. Câu 29: Phương pháp: Dao động tổng hợp có tần số bằng tần số của các dao động thành phần. Biên độ dao động tổng hợp: \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \Delta \varphi } \) Độ lớn vận tốc, gia tốc cực đại: \(\left\{ \begin{array}{l}{v_{\max }} = \omega A\\{a_{\max }} = {\omega ^2}.A\end{array} \right.\) Cách giải: Độ lớn của vận tốc, gia tốc cực đại là: \(\left\{ \begin{array}{l}{v_{\max }} = \omega A\\{a_{\max }} = {\omega ^2}.A\end{array} \right.\\ \Rightarrow A = \frac{{v_{\max }^2}}{{{a_{\max }}}} = \frac{{{1^2}}}{4} = 0,{25_{}}m = {25_{}}cm\) Biên độ dao động tổng hợp là: \(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \Delta \varphi } \\ \Rightarrow 25 = \sqrt {{7^2} + A_2^2 + 2.7.{A_2}.\cos \left( {\frac{\pi }{{12}} - \frac{{7\pi }}{{12}}} \right)} \\ \Rightarrow {A_2} = {24_{}}cm\end{array}\) Chọn A. Câu 30: Phương pháp: Trong một chu kì, phần tử sóng đi được quãng đường là \(S = 4A\), sóng truyền đi được một bước sóng. Công thức tính tốc độ truyền sóng và tốc độ trung bình trong một chu kì của một phần tử là \(\left\{ \begin{array}{l}v = \frac{\lambda }{T}\\{v_{tb}} = \frac{{4A}}{T}\end{array} \right.\) Cách giải: Trong một chu kì, phần tử sóng đi được quãng đường là \(S = 4A\), sóng truyền đi được một bước sóng. Công thức tính tốc độ truyền sóng và tốc độ trung bình trong một chu kì của một phần tử là: \(\left\{ \begin{array}{l}v = \frac{\lambda }{T}\\{v_{tb}} = \frac{{4A}}{T}\end{array} \right. \Rightarrow v = {v_{tb}} \Rightarrow \lambda = 4A\) Chọn D. Câu 31: Phương pháp: Chu kì của con lắc lò xo treo thẳng đứng: \(T = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \) Sử dụng VTLG để tính biên độ con lắc. Cách giải: Chu kì của con lắc là: \(T = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} = 0,2 \\\Rightarrow \Delta {l_0} = 0,01m = 1cm\) Trong một chu kì, thời gian giãn lớn gấp 3 lần thời gian lò xo bị nén. Ta có VTLG : Thời gian lò xo nén trong một chu kì là: \(t = \frac{\alpha }{{2\pi }}.T = \frac{{2\arccos \frac{{\Delta {l_0}}}{A}}}{{2\pi }}.T\) Thời gian lò xo dãn bằng ba lần thời gian nén nên ta có: \(\begin{array}{l}t = \frac{\alpha }{{2\pi }}.T = \frac{{2\arccos \frac{{\Delta {l_0}}}{A}}}{{2\pi }}.T = \frac{1}{4}.T\\ \Rightarrow \arccos \frac{{\Delta {l_0}}}{A} = \frac{\pi }{4} \\\Rightarrow \frac{{\Delta {l_0}}}{A} = \frac{{\sqrt 2 }}{2} \Rightarrow \Delta {l_0} = \frac{1}{{\sqrt 2 }}A \Rightarrow A = \sqrt 2 cm\end{array}\) Cơ năng của con lắc là: \({\rm{W}} = \frac{1}{2}.k.{A^2} = \frac{1}{2}.m.{\omega ^2}.{A^2} = \frac{1}{2}.m.{\left( {\frac{{2\pi }}{T}} \right)^2}{A^2} \\= 0,02J\) Chọn C. Câu 32: Phương pháp: Áp dụng công thức tính bước sóng \(\lambda = v.T = \frac{v}{f}\) Hai điểm cách nhau một số nguyên lần bước sóng thì dao động cùng pha. Hai điểm cách nhau nửa bước sóng thì dao động ngược pha. Hai điểm cách nhau một phần tư bước sóng thì dao động vuông pha. Theo chiều truyền sóng, sườn sóng trước đi lên thì sườn sóng sau đi xuống. Cách giải: Nhìn vào hình ảnh, ta thấy A và C cách nhau nửa bước sóng nên A và C ngược pha. Nên ta có: \(\frac{\lambda }{2} = 40cm \Rightarrow \lambda = 80cm\) Vận tốc truyền sóng: \(v = \frac{\lambda }{T} = \lambda .f = 80.5 = {400_{}}cm/s = {4_{}}m/s\) B và C cách nhau một phần tư bước sóng nên B và C vuông pha. Vì C đi xuống nên sóng truyền từ E đến A. Vậy phát biểu B sai. Chọn B. Câu 33: Phương pháp: Sử dụng VTLG Áp dụng công thức tính cơ năng, động năng, thế năng \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m.{v^2} + \frac{1}{2}.k.{x^2} \\= \frac{1}{2}.k.{A^2}\) Khi vật đi từ vị trí cân bằng và chưa đổi chiều chuyển động thì tốc độ giảm còn một nửa, ta tìm được vị trí x theo A. Từ đó tính được chu kì T. Trong khoảng thời gian từ thời điểm t2 đến thời điểm t3 = t2 + 1,5s, vật đi được quãng đường 20 cm ta tìm được biên độ. Áp dụng VTLG để tìm quãng đường lớn nhất vật đi được trong 5s Cách giải: Tại thời điểm t1, vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t1 đến thời điểm t2 = t1 + 0,5 s vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Ta có VTLG: Tại thời điểm t2 thì vận tốc chỉ còn một nửa, do đó ta có: \({{\rm{W}}_d} = \frac{1}{2}.m{v^2} = \frac{1}{2}.m.{\left( {\frac{{{v_{\max }}}}{2}} \right)^2} \\= \frac{1}{4}.m.v_{\max }^2\) Do đó, thế năng là: \({{\rm{W}}_t} = \frac{3}{4}{\rm{W}} \Rightarrow \frac{1}{2}.k.{x^2} = \frac{3}{4}.\frac{1}{2}.k.{A^2} \\\Rightarrow x = \frac{{\sqrt 3 }}{2}A\) Thời gian: \({t_2} - {t_1} = 0,5 = \frac{{\frac{\pi }{2} - \arccos \frac{x}{A}}}{{2\pi }}.T \Leftrightarrow 0,5 = \frac{T}{6} \\\Rightarrow T = 3s\) Trong khoảng thời gian từ thời điểm t2 đến thời điểm t3 = t2 + 1,5s, vật đi được quãng đường 20 cm Vậy \({t_3} - {t_2} = 1,5 = \frac{T}{2} \Rightarrow S = 2A = 20cm\\ \Rightarrow A = 10cm\) Ta có VTLG : Trong thời gian 5s = 1,5T + 0,5s vật đi được quãng đường là S = 6A + ∆s Để S cực đại thì ∆s cực đại, ta có VTLG: Ta có \(\Delta s = 2.A.\cos \left( {\frac{\pi }{2} - \frac{{0,5}}{{2T}}.2\pi } \right) = 10cm\) Vậy quãng đường cực đại là S = 6A+ 10 = 70 cm Chọn B. Câu 34: Phương pháp: Áp dụng công thức tính chu kì: \(T = 2\pi \sqrt {\frac{l}{g}} \Rightarrow \overline g = \frac{{4{\pi ^2}.l}}{{{T^2}}}\) Sai số tỉ đối: \(\delta g = \delta l + 2\delta T\) Sai số: \(\Delta g = \delta g.\overline g \) Viết kết quả: \(g = \overline g \pm \Delta g\) Cách giải: Áp dụng công thức tính chu kì: \(T = 2\pi \sqrt {\frac{l}{g}} \Rightarrow \overline g = \frac{{4{\pi ^2}.l}}{{{T^2}}} = \frac{{4{\pi ^2}.0,8}}{{1,{8^2}}}\\ = 9,{75_{}}m/{s^2}\) Sai số tỉ đối: \(\delta g = \delta l + 2\delta T = \frac{{0,1}}{{80}} + 2.\frac{{0,02}}{{1,8}} = 2,35\% \) Sai số: \(\Delta g = \delta g.\overline g = 2,35\% .9,75 = 0,{23_{}}m/{s^2}\) Giá tốc trọng trường: \(g = \overline g \pm \Delta g = (9,75 \pm 0,23)m/{s^2}\) Chọn D. Câu 35: Phương pháp: Trong một chu kì, khoảng thời gian mà lực đàn hồi tác dụng lên vật nặng có chiều hướng từ trên xuống dưới là là thời gian lò xo bị nén. Tại vị trí cân bằng lò xo dãn một đoạn ∆l0 Công thức tính cơ năng: \({\rm{W}} = \frac{1}{2}.k.{A^2}\) Công thức tính chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} \) Sử dụng VTLG Cách giải: Tại vị trí cân bằng lò xo dãn một đoạn ∆l0, ta có: \(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,4.10}}{{100}} = 0,04m = 4cm\) Công thức tính cơ năng: \({\rm{W}} = \frac{1}{2}.k.{A^2} \Rightarrow 0,16 = \frac{1}{2}.100.{A^2}\\ \Rightarrow A = 4{\sqrt 2 _{}}cm\) Công thức tính chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi .\sqrt {\frac{{0,4}}{{100}}} = 0,4s\) Ta có VTLG: Thời gian lò xo bị nén trong một chu kì là: \(t = \frac{{2\arccos \frac{{\Delta {l_0}}}{A}}}{{2\pi }}.T = \frac{T}{4} = \frac{{0,1}}{4} = 0,1s\) Chọn A. Câu 36: Phương pháp: Khoảng cách giữa hai chất điểm M và N là: \(\left| x \right| = \left| {{x_N} - {x_M}} \right|\\ \Rightarrow A = \sqrt {A_N^2 + A_M^2 - 2{A_N}{A_M}.\cos \Delta \varphi } \) Từ đó ta tìm được độ lệch pha giữa M và N. Ở thời điểm mà M có động năng bằng ba lần thế năng tìm ra tọa độ của N khi đó. Áp dụng công thức tính vận tốc: \({v^2} = {\omega ^2}.({A^2} - {x^2})\) rồi lập tỉ số động năng của M và động năng của N. Sử dụng VTLG Cách giải: Khoảng cách giữa hai chất điểm M và N là \(\begin{array}{l}x = {x_N} - {x_M} \\\Rightarrow A = \sqrt {A_N^2 + A_M^2 - 2{A_N}{A_M}.\cos \Delta \varphi } \\ \Leftrightarrow 17 = \sqrt {{{15}^2} + {8^2} - 2.15.8.\cos \Delta \varphi } \\ \Leftrightarrow \Delta \varphi = \frac{\pi }{2}\end{array}\) Ở thời điểm mà M có động năng bằng ba lần thế năng tức là thế năng bằng một phần tư cơ năng, ta có \({{\rm{W}}_t} = \frac{1}{4}{\rm{W}} \Rightarrow \frac{1}{2}.k.{x_M}^2 = \frac{1}{4}.\frac{1}{2}.k.A_M^2 \\\Rightarrow {x_M} = \frac{{{A_M}}}{2}\) Sử dụng VTLG: Ta có \({x_N} = {A_N}.\cos \left( {\frac{\pi }{2} - \arccos \frac{{{x_M}}}{{{A_M}}}} \right) = {A_N}.\frac{{\sqrt 3 }}{2}\) Áp dụng công thức tính vận tốc \({v^2} = {\omega ^2}.({A^2} - {x^2})\) Ta có tỉ số động năng giữa M và N là: \(\frac{{{{\rm{W}}_{dM}}}}{{{{\rm{W}}_{dN}}}} = \frac{{\frac{1}{2}.m.v_M^2}}{{\frac{1}{2}.m.v_M^2}} = \frac{{{\omega ^2}.(A_M^2 - x_M^2)}}{{{\omega ^2}.(A_N^2 - x_N^2)}} = \frac{{\frac{3}{4}A_M^2}}{{\frac{1}{4}A_N^2}} \\= 3.\frac{{{8^2}}}{{{{15}^2}}} = \frac{{64}}{{75}}\) Chọn D. Câu 37: Phương pháp: Từ đồ thị ta xác định được \(\left\{ \begin{array}{l}\lambda = 24\\MN = 10\end{array} \right. \Rightarrow \Delta {\varphi _{MN}}\) Khoảng cách giữa M và N là \(d = \sqrt {M{N^2} + {{({x_M} - {x_N})}^2}} \) Tìm phương trình của \(x = {x_M} - {x_N}\) , khoảng cách MN cực đai khi x cực đại. Cách giải: Từ đồ thị ta xác định được \(\left\{ \begin{array}{l}\lambda = 24\\MN = 10\end{array} \right. \Rightarrow \Delta {\varphi _{MN}} = \frac{{10}}{{24}}.2\pi = \frac{{5\pi }}{6}\) Khoảng cách giữa M và N là \(d = \sqrt {M{N^2} + {{({u_M} - {u_N})}^2}} \) Gọi \(u = {u_M} - {u_N}\) , khoảng cách MN cực đại khi u cực đại. Ta có: \({u_{\max }} = \sqrt {A_M^2 + A_N^2 - 2{A_M}.{A_N}.\cos \Delta \varphi }\\ = \sqrt {{{2.5}^2} - 2.5.5.\cos \frac{{5\pi }}{6}} = 9,66cm\) Khoảng cách cực đại giữa M và N là: \(d = \sqrt {M{N^2} + {{({x_M} - {x_N})}^2}}\\ = \sqrt {{{10}^2} + 9,{{66}^2}} = 13,90cm\) Chọn A. Câu 38: Phương pháp: Trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có động năng không vượt quá ba lần thế năng là 2s dùng để xác định chu kì T. Sử dụng VTLG. Trong 1 chu kì con lắc đi qua vị trí x = 2 cm theo chiều dương 1 lần Vì vậy thời gian để con lắc đi qua vị trí x = 2 cm theo chiều dương lần thứ 2018 là t = 2017T + ∆t Với ∆t là thời gian từ thời điểm ban đầu đến khi còn lắc qua vị trí x = 2 lần đầu tiên. Cách giải: Vị trí động năng bằng 3 lần thế năng, tức là thế năng bằng \(\frac{1}{4}\) cơ năng, ta có: \(x = \pm \frac{A}{2}\) cm Ta có VTLG:
Thời gian mà động năng không vượt quá ba lần thế năng là: \(t = \frac{{4{\rm{arc}}\cos \frac{{\frac{A}{2}}}{A}}}{{2\pi }}.T = \frac{T}{3} = 2s \Rightarrow T = 6s\) Vì vậy thời gian để con lắc đi qua vị trí x = 2 cm theo chiều dương lần thứ 2018 là t = 2017T + ∆t Với ∆t là thời gian từ thời điểm ban đầu đến khi còn lắc qua vị trí x = 2 lần đầu tiên. Ta có \(\Delta t = \frac{{\arccos \frac{2}{4}}}{{2\pi }}T = \frac{T}{6} = 1s\) t = 2017T + ∆t = 2017.6 + 1 = 12103s Chọn A. Câu 39: Phương pháp: Chu kì \(T = \frac{1}{f}\) Tại vị trí lò xo có chiều dài lớn nhất tức là vật ở biên dương. Thời gian \(t = \frac{1}{3}s = T + \frac{1}{4}T + \frac{1}{{30}}s\) Vậy quãng đường S = 4A + A + ∆s Tốc độ trung bình \({v_{tb}} = \frac{S}{{\Delta t}}\) Vận tốc trung bình \({V_{tb}} = \frac{{\left| {{x_1} - {x_2}} \right|}}{{\Delta t}}\) Sử dụng VTLG để xác định quãng đường và độ dời của vật. Cách giải: Chu kì \(T = \frac{1}{f} = \frac{1}{5} = 0,2s\) Tại vị trí lò xo có chiều dài lớn nhất tức là vật ở biên dương. Thời gian \(t = \frac{1}{3}s = T + \frac{1}{4}T + \frac{1}{{20}}s\) Ta có VTLG Quãng đường S = 4A + ∆s = 4A + A + ∆s Góc a có giá trị là \(a = \frac{\pi }{2} - \frac{{\frac{1}{{20}}}}{{\frac{1}{3}}}.2\pi = \frac{\pi }{5}\) Ta có \({x_1} = A.\cos \left( {\frac{\pi }{5}} \right)\) Tốc độ trung bình \({v_{tb}} = \frac{S}{{\Delta t}} = \frac{{5A + A.\cos \frac{\pi }{5}}}{{\Delta t}}\) Vận tốc trung bình \({V_{tb}} = \frac{{\left| {{x_1} - {x_2}} \right|}}{{\Delta t}} = \frac{{A + A.\cos \frac{\pi }{5}}}{{\Delta t}}\) Tỉ số giữa tốc độ trung bình và độ lớn vận tốc trung bình của vật là \(\frac{{5A + A.\cos \frac{\pi }{5}}}{{A + A.\cos \frac{\pi }{5}}} = 3,21\) Giá trị gần nhất là 3. Chọn B. Câu 40: Phương pháp: Đồ thị mô tả chuyển động của con lắc từ biên dương về biên âm (hoặc từ biên âm về biên dương) Từ đồ thị ta thấy động năng cực đại là 2J, tại 0,1s và 0,3 s thì động năng bằng một nửa giá trị cực đại. Tại t1 thì động năng là 1,8J, vậy thế năng là 2 - 1,8 = 0,2 J, nên động năng bằng 9 lần thế năng. Tại t2 thì động năng bằng 1,6 J, vậy thế năng là 0,4J. Cách giải: Đồ thị mô tả chuyển động của con lắc từ biên dương về biên âm (hoặc từ biên âm về biên dương) Từ đồ thị ta thấy động năng cực đại là 2J, tại 0,1s và 0,3 s thì động năng bằng một nửa giá trị cực đại. Tại 0,1 s thì \({{\rm{W}}_d} = \frac{{\rm{W}}}{2} \Rightarrow {{\rm{W}}_d} = {{\rm{W}}_t} = \frac{{\rm{W}}}{2}\\ \Rightarrow x = \frac{A}{{\sqrt 2 }} \Rightarrow 0,1s = \frac{T}{8} \Rightarrow T = 0,8s\) Tại t1 thì động năng là 1,8J, vậy thế năng là 2 - 1,8 = 0,2 J, nên động năng bằng 9 lần thế năng. Tại t2 thì động năng bằng 1,6 J, vậy thế năng là 0,4J. \(\left\{ \begin{array}{l}{{\rm{W}}_d} = 1,8J\\{{\rm{W}}_d} = 1,6J\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\frac{{{{\rm{W}}_{t1}}}}{{\rm{W}}} = \frac{{0,2}}{2} = \frac{{x_1^2}}{{{A^2}}} = \frac{1}{{10}}\\\frac{{{{\rm{W}}_{t2}}}}{{\rm{W}}} = \frac{{0,4}}{2} = \frac{{x_2^2}}{{{A^2}}} = \frac{1}{5}\end{array} \right. \\\Rightarrow \left\{ \begin{array}{l}{x_1} = \pm \frac{A}{{\sqrt {10} }}\\{x_2} = \pm \frac{A}{{\sqrt 2 }}\end{array} \right.\) Từ VTLG ta có: \({t_2} - {t_1} = \frac{1}{\omega }\left( {\arcsin \frac{{{x_1}}}{A} + \arcsin \frac{{{x_2}}}{A}} \right) = 0,1s\) Vậy phát biểu B là chưa đúng. Chọn B. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
