Đề kiểm tra 45 phút (1 tiết) - Đề số 7 - Chương 3 - Hình học 7

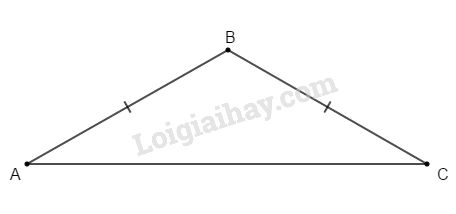
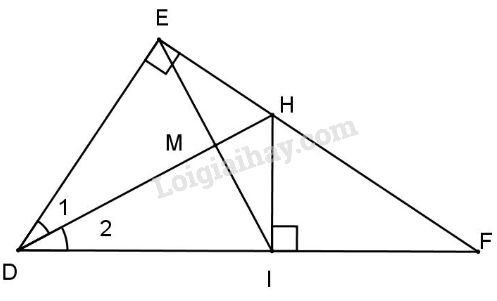
Đề bài

Bài 1: Cho tam giác ABC cân tại B có góc B tù.

a) So sánh độ dài hai cạnh AB và AC.

b) Biết số đo góc A bằng \({25^0}\). Tính số đo góc B và góc C.

Bài 2: Cho tam giác DEF có \(\widehat E = {90^0},\) tia phân giác DH. Qua H kẻ HI vuông góc với DF (I thuộc DF). Chứng minh:

a) \(\Delta DHE = \Delta DHI\).

b) DH là đường trung trực của đoạn  EI.

c) \(EH < HF.\)

LG bài 1

Phương pháp giải:

 +Trong một tam giác độ dài 1 cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại

+Tổng ba góc của tam giác bằng 180 độ

Lời giải chi tiết:

a) Ta có: \(\widehat B > \widehat A = \widehat C\) (vì \(\widehat B\) tù)

\( \Rightarrow AC > AB\) (quan hệ cạnh và góc)

b) Ta có \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng các góc trong tam giác)   
mà \(\widehat A = \widehat C = {25^0}\) 
\(\eqalign{ &  \Rightarrow 2\widehat A + \widehat B = {180^0}  \cr   &  \Rightarrow \widehat B = {130^0}. \cr} \)

LG bài 2

Phương pháp giải:

Hai góc kề bù có tổng bằng 180 độ

Trong tam giác vuông cạnh góc vuông nhỏ hơn cạnh huyền

Lời giải chi tiết:

a) Xét \(\Delta DHE\) và \(\Delta DHI\) có 

+) \(\widehat {DEH} = \widehat {DIH} = {90^0}\) (gt)

+) DH: cạnh chung

+) \({\widehat D_1} = {\widehat D_2}\) (gt)

Do đó \(\Delta DHE = \Delta DHI\) (cạnh huyền góc nhọn).

b) Gọi M là giao điểm của EI và DH.

Xét \(\Delta DME\) và \(\Delta DMI\) có:

+) DM cạnh chung,

+) \({\widehat D_1} = {\widehat D_2}\) (gt);

+) DE = DI (cmt).

Do đó \(\Delta DME = \Delta DMI\) (c.g.c)

\( \Rightarrow \widehat {DME} = \widehat {DMI}\) mà \(\widehat {DME} + \widehat {DMI} = {180^0}\) (kề bù)

\( \Rightarrow \widehat {DME} = \widehat {DMI} = {90^0}\) hay \(DH \bot EI\)

Lại có \(ME = MI\) (cạnh tương ứng)

\( \Rightarrow DH\) là đường trung trực của đoạn EI.

c) Theo câu a) ta có: \(\Delta DHE = \Delta DHI\) nên HI=HE

Xét tam giác HIE vuông tại H có HF là cạnh huyền nên HI

Suy ra HE<HF. 

HocTot.Nam.Name.Vn