Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 3 - Hình học 7

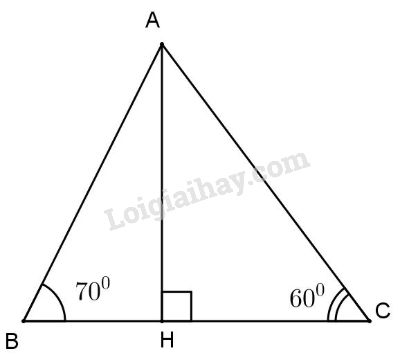
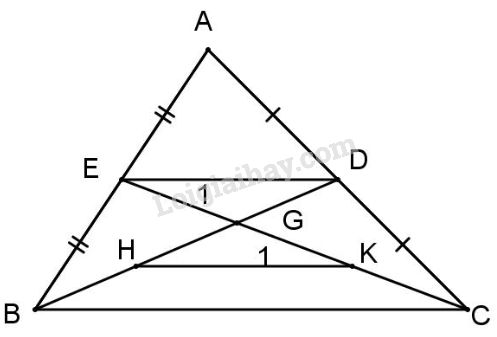
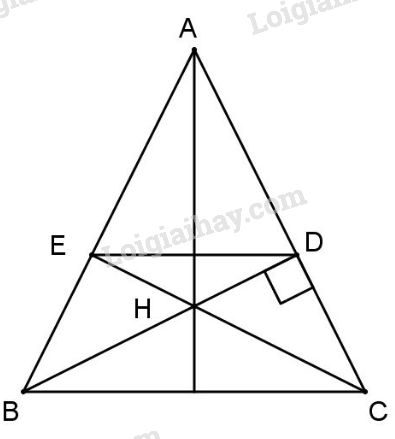
Đề bài

Bài 1: Cho tam giác ABC có $\widehat B = {70^0},\widehat C = {60^0},$ vẽ đường cao AH. Hãy so sánh độ dài các đoạn HB và HC.

Bài 2: Cho tam giác ABC nhọn,  hai trung tuyến BD và CE cắt nhau tại G. Gọi H, K lần lượt là trung điểm của GB và GC. Chứng minh DE // HK.

Bài 3: Cho tam giác ABC  cân tại A ($AB > AC$), hai đường cao BD và CE cắt nhau tại H. Chứng minh:

a) $\Delta AB{\rm{D}}$ và $\Delta AC{\rm{E}}$ bằng nhau;

b) AH là đường trung trực của đoạn BC;

c) DE và BC song song với nhau;

d) $AH > CH.$  

LG bài 1

Phương pháp giải:

+ Trong 1 tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn

+Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

Lời giải chi tiết:

a) Ta có $\widehat B > \widehat C$ (${70^0} > {60^0}$ (gt)

$\Rightarrow AC > AB$ (quan hệ góc cạnh trong tam giác)

$\Rightarrow HC > HB$ (quan hệ đường xiên hình chiếu).

LG bài 2

Phương pháp giải:

Tính chất trọng tam tam giác

Nếu 1 đường thẳng cắt hai đường thẳng, các cặp góc tạo thành có 1 cặp góc so le trong bằng nhau thì hai đường thẳng đó song song

Lời giải chi tiết:

BD và CE là hai trung tuyến cắt nhau tại G nên G là trọng tâm $\Delta ABC.$

Ta có $GB = 2G{\rm{D}}$ và $GC = 2GE$ (tính chất trọng tâm);

H, K lần lượt là trung điểm của GB và GC (gt)  

$\Rightarrow GH = G{\rm{D}}$ và $GK = GE.$

Do đó $\Delta {\rm E}G{\rm{D}} = \Delta KGH$ (c.g.c)

${\widehat E_1} = {\widehat K_1}$ (góc tương ứng)

Do đó ED // HK (cặp góc so le trong bằng nhau).

LG bài 3

Phương pháp giải:

+Ba đường cao của tam giác đồng quy tại 1 điểm

+Nếu 1 đường thẳng cắt hai đường thẳng, các cặp góc tạo thành có 1 cặp góc so le trong bằng nhau thì hai đường thẳng đó song song

+Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:

a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn

b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn

Lời giải chi tiết:

a) Xét $\Delta A{\rm{D}}B$ và $\Delta A{\rm{E}}C$ có 

+) $AB = AC$ (gt);

+) $\widehat A$: chung.

Do đó $\Delta A{\rm{D}}B = \Delta A{\rm{E}}C$ (cạnh huyền – góc nhọn).

b) BD và CE là hai đường cao của $\Delta ABC$ (gt), mà BD cắt CE tại H là trực tâm.

Mặt khác, $\Delta ABC$ cân tại A (gt) nên đường cao AH cũng đồng thời là đường trung trực của BC.

c) Ta có $\Delta A{\rm{D}}B = \Delta A{\rm{E}}C$ (cmt)

$\Rightarrow A{\rm{D}} = A{\rm{E}}.$ Do đó $\Delta A{\rm{D}}E$ cân tại A, ta có

$\widehat {A{\rm{ED}}} = \widehat {A{\rm{D}}E} = \dfrac{{{{180}^0} - \widehat A} }{ 2}$    (1).

Tương tự $\Delta ABC$ cân tại A, ta có

$\widehat {ABC} = \widehat {ACB} = \dfrac{{{{180}^0} - \widehat A} }{2}$    (2).

Từ (1) và (2) $\Rightarrow \widehat {A{\rm{ED}}} = \widehat {ABC} = \dfrac{{{{180}^0} - \widehat A}}{ 2} \Rightarrow$

ED// BC (cặp góc so le trong bằng nhau).

d) Ta có $AB > BC$ (gt) $\Rightarrow A{\rm{D}} > C{\rm{D}}$ (quan hệ đường xiên hình chiếu) $\Rightarrow AH > CH.$ 

HocTot.Nam.Name.Vn