Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 2 - Hình học 7Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 2 - Hình học 7
Lựa chọn câu để xem lời giải nhanh hơn
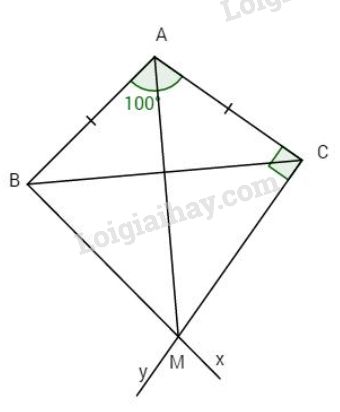
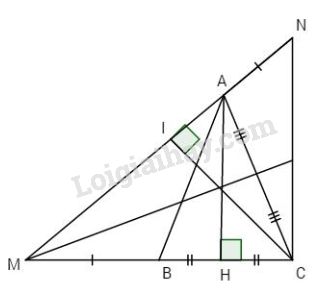
Đề bài Bài 1. Bằng tính toán hãy xét xem tam giác sau đây có vuông hay không, nếu vuông thì vuông tại đỉnh nào? Biết MN = \(\sqrt 3 \,;\,NP = \sqrt 5 ;\,\) và \(MP =\sqrt 2 .\) Bài 2. Cho tam giác ABC cân tại A có \( \Rightarrow MI = NI,\) \(\widehat A = {100^o}\), kẻ Bx vuông góc với AB tại B, Cy vuông góc với AC tại C. Gọi M là giao điểm của Bx và Cy. a) Tính các góc của tam giác BMC. b) Chứng minh rằng AM là đường trung trực của BC. Bài 3. Cho tam giac ABC có \(\widehat A = {40^o}\); AB = AC. Gọi H là trung điểm của BC. a) Tính \(\widehat {ABC},\,\widehat {ACB}\) và chứng minh AH vuông góc với BC. b) Trung trực của đoạn AC cắt tia CB ở M. Tính \(\widehat {MAH}\). c) Trên tia đối của tia MA lấy điểm N sao cho AN = BM. Chứng minh AM = CN. d) Vẽ CI vuông góc với MN tại I. Chứng minh I là trung điểm của MN. LG bài 1 Phương pháp giải: Áp dụng định lý Py-ta-go Lời giải chi tiết: Ta có \({\left( {\sqrt 3 } \right)^2} + {\left( {\sqrt 2 } \right)^3} = {\left( {\sqrt 5 } \right)^2}\)\(\,\left( {M{N^2} + M{P^2} = N{P^2}} \right)\) Theo định lí Pytago đảo ta có \(\Delta MNP\) vuông tại M. LG bài 2 Phương pháp giải: Tam giác cân có hai góc ở đáy bằng nhau và 2 cạnh bên bằng nhau Tổng ba góc của 1 tam giác bằng 180 độ Lời giải chi tiết:
a) \(\Delta ABC\) cân tại A có \(\widehat A = {100^o}\) \( \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac{{{{180}^o} - {{100}^o}}}{ 2} \)\(\,= {40^o}\) \(Bx \bot AB\) (giả thiết) \( \Rightarrow \widehat {ABx} = {90^o}\) \( \Rightarrow \widehat {CBx} = {90^o} - \widehat {ABC} = {90^o} - {40^o} \)\(\;= {50^o}\) Tương tự ta có \(\widehat {CBy} = {50^o}\) Do đó \(\widehat {BMC} = {180^o} - \left( {\widehat {CBx} + \widehat {BCy}} \right)\) \( = {180^o} - {100^o} = {80^o}.\) b) Ta có \(\widehat {BCy} = \widehat {BCx} = {50^o}\) nên \(\Delta BMC\) cân tại M \( \Rightarrow MB = MC.\) Lại có AB = AC (giả thiết). Do đó AM là đường trung trực của BC. LG bài 3 Phương pháp giải: Tam giác cân có hai góc ở đáy bằng nhau Tổng ba góc của 1 tam giác bằng 180 độ Hai góc kề bù có tổng bằng 180 độ Lời giải chi tiết:
a) Ta có \(\Delta ABC\) cân tại A có \(\widehat A = {40^o}\) \( \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac {{{{180}^o} - \widehat A}}{ 2} \)\(\;=\dfrac {{{{180}^o} - {{40}^o}} }{ 2} = {70^o}\) H là trung điểm của BC (giả thiết) \( \Rightarrow HB = HC\), lại có AB = AC (giả thiết). Do đó \(\Delta AHB = \Delta AHC\)(c.c.c). \( \Rightarrow \widehat {HAB} = \widehat {HAC}\) (góc tương ứng), mà \(\widehat {HAB} + \widehat {HAC} = {180^o}\)(kề bù) \(\widehat {HAB} = \widehat {HAC} = {90^o}\) hay \(AH \bot BC.\) b) M thuộc trung trực của đoạn AC nên MA = MC. Do đó \(\Delta AMC\) cân tại M \( \Rightarrow \widehat {MAC} = \widehat {BCA} = {70^o}\). Lại có \(\Delta AHB = \Delta AHC\) (chứng minh trên) \( \Rightarrow \widehat {HAB} = \widehat {HAC} = \dfrac{{\widehat {BAC}} }{2} \)\(\;= \dfrac{{{{40}^o}} }{ 2} = {20^o}\) \(\widehat {MAH} = \widehat {MAC} - \widehat {HAC} \)\(\;= {70^o} - {20^o} = {50^o}.\) c) Ta có \(\widehat {NAC} + \widehat {MAC} = {180^o}\) (kề bù) \( \Rightarrow \widehat {NAC} = {180^o} - \widehat {MAC}\)\(\; = {180^o} - {70^o} = {110^o}.\) Xét \(\Delta ABM\) và \(\Delta CAN\) có: AB = AC (giả thiết) Chứng minh tương tự ta có \(\widehat {MBA} = {110^o}\) (vì \(\widehat {ABC} = {70^o}\)) \(\widehat {ABM} = \widehat {CAN} = {110^o}\) (chứng minh trên) MB = NA (giả thiết). Do đó \(\Delta ABM = \Delta CAN\) (c.g.c) \( \Rightarrow AM = CN\) (cạnh tương ứng). d) Ta có MA = MC (chứng minh trên) \( \Rightarrow MC = NC.\) Xét \(\Delta MIC\) và \(\Delta NIC\) có: +) \(\widehat {MIC} = \widehat {NIC} = {90^o}\) (giả thiết), +) MC = NC (chứng minh trên), +) IC chung. Vậy \(\Delta MIC\)= \(\Delta NIC\) (ch.cgv) \( \Rightarrow MI = NI\) hay I là trung điểm của MN. HocTot.Nam.Name.Vn
|