Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 2 - Hình học 7

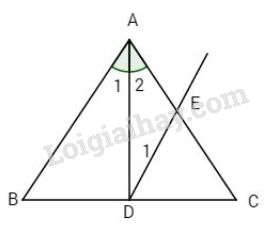
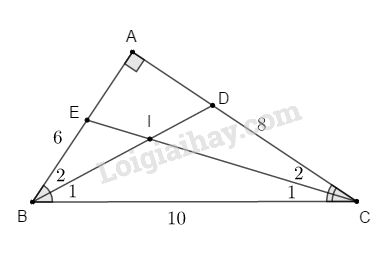
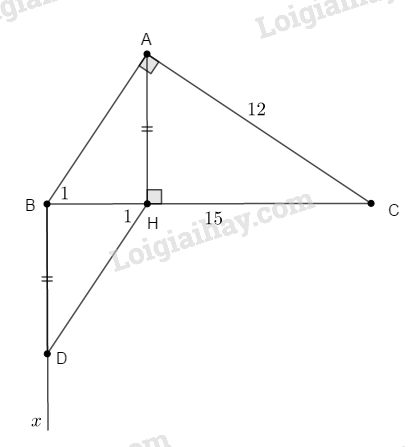
Đề bài

Bài 1. Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác ADE là tam giác cân.

Bài 2. Cho tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm.

a) Chứng tỏ tam giác ABC vuông.

b) Kẻ phân giác BD và CE (D thuộc AC, E thuộc AB), BD và CE cắt nhau tại I. Tính $\widehat {BIC}$

Bài 3. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc vẽ tia Bx song song với AH). Trên Bx lấy D sao cho BD = AH.

a) Chứng minh $\Delta AHB$ và $\Delta DHB$ bằng nhau.

b) Nếu AC = 12cm; BC =15cm. Tính độ dài DH.

LG bài 1

Phương pháp giải:

Nếu 1 đường thẳng cắt hai đường thẳng song song thì: Các cặp góc so le trong bằng nhau.

Lời giải chi tiết:

Ta có Dx // AB (giả thiết) $\Rightarrow \widehat {{D_1}} = \widehat {{A_1}}$ (cặp góc so le trong). Mà $\widehat {{A_1}} = \widehat {{A_2}}$(giả thiết). Do đó $\widehat {{D_1}} = \widehat {{A_2}}$. Vậy $\Delta ADE$ cân tại E.

LG bài 2

Phương pháp giải:

Đường phân giác của 1 góc chia đôi góc đó thành 2 góc bằng nhau

Tổng ba góc của 1 tam giác bằng 180 độ

Định lý Py-ta-go

Lời giải chi tiết:

a) Ta có $A{B^2} + A{C^2} = B{C^2}\,({6^2} + {8^2} = {10^2})$

Do đó theo định lý Pytago đảo ta có $\Delta ABC$ vuông tại A. 

$\Rightarrow \widehat B + \widehat C = {180^o} - \widehat A$$\;= {180^o} - {90^o} = {90^o}$

b) Ta có $\widehat A + \widehat B + \widehat C = {180^o}$

Suy ra $\widehat B + \widehat C = {180^o}-\widehat A=90^0$

$\displaystyle \Rightarrow {{\widehat B} \over 2} + {{\widehat C} \over 2} = {45^o}$

Mà $\widehat {{B_1}} = \dfrac{{\widehat B}}{2};\widehat {{C_1}} = \dfrac{{\widehat C}}{2}$ (tính chất tia phân giác)

Nên $\widehat {{B_1}} + \widehat {{C_1}} = {45^o}$

Xét $\Delta BIC$ có $\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = {180^o}$

$\Rightarrow \widehat {BIC} = {180^o} - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right)$$\; = {180^o} - {45^o} = {135^o}$

LG bài 3

Lời giải chi tiết:

a) Ta có:

$AH \bot BC$ (giả thiết)

$BD//AH$ (giả thiết)

$\Rightarrow BD \bot BC$ hay $\Delta DBH$ vuông tại B.

Mặt khác BD // AH $\Rightarrow \widehat {{B_1}} = \widehat {{H_1}}$(cặp góc so le trong).

Do đó hai tam giác vuông $\Delta DBH = \Delta AHB$ (g.c.g).

b) $\Delta ABC$ vuông tại A (giả thiết). Theo định lí Pytago ta có:

$A{B^2} + A{C^2} = B{C^2}$

$\Rightarrow A{B^2} = B{C^2} - A{C^2}$$\; = {15^2} - {12^2} = 225 - 144 = 81$

$\Rightarrow AB = \sqrt {81}  = 9\,(cm)$

Ta có $\Delta DBH = \Delta AHB$ (chứng minh trên) $\Rightarrow DH = AB = 9\,(cm)$(cạnh tương ứng).

HocTot.Nam.Name.Vn