Đề kiểm tra 45 phút ( 1 tiết) - Đề số 5 - Chương 1 - Hình học 8

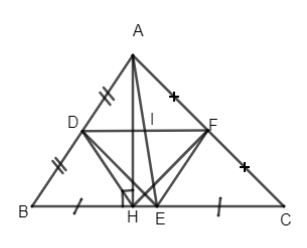
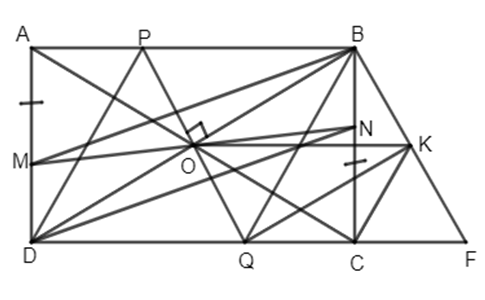
Đề bài

Bài 1. Cho tam gác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE. 

a) Chứng  minh tứ giác DFEH là hình thang cân.

b) Chứng minh I là trung điểm của DF.

Bài 2. Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.

a) Chứng minh rằng: $BM\parallel DN.$

b) Gọi O là trung điểm của BD. Chứng minh AC, BD, MN đồng quy tại O.

c) Qua O vẽ đường thẳng d vuông góc với BD, d cắt cạnh AB tại P, cắt cạnh CD tại Q. Chứng minh rằng PBQD là hình thoi.

d) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. Chứng minh rằng: $AC \bot CK.$

LG bài 1

Phương pháp giải:

Sử dụng:

Tứ giác có hai cạnh đối song song là hình thang

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền

Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy

Lời giải chi tiết:

a) Ta có DF là đường trung bình của $\Delta ABC$ nên $DF\parallel BC$ hay $DF\parallel HE.$

Do đó DFEH là hình thang. 

Mặt khác $\Delta AHC$ vuông có HF là đường trung tuyến nên $HF = {1 \over 2}AC.$

DE là đường trung bình của $\Delta ABC$

$\Rightarrow DE = {1 \over 2}AC$

b) Ta có $DE\parallel BC$ (cmt) hay $DI\parallel BE.$ Do đó DI là đường trung bình của $\Delta ABE \Rightarrow I$ là trung điểm của AE và $DI = {1 \over 2}BE$

Trong $\Delta AEC$ có IF là đường trung bình nên $IF = {1 \over 2}EC$ mà EC = EB (gt)

$\Rightarrow IF = ID$ hay I là trung điểm của DF.

LG bài 2

Phương pháp giải:

Sử dụng: 

Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành

Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền

Lời giải chi tiết:

a)Ta có AD = BC và $AD\parallel BC\left( {gt} \right)$, AM = CN (gt)

$\Rightarrow AD - AM = BC - CN$

Hay DM = BN,

Lại có $DM\parallel BN,$

Do đó BMDN là hình bình hành

$\Rightarrow BM\parallel DN.$

b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.

Lại có tứ giác BMDN là hình bình hành nên MN phải qua trung điểm O của BD. Vậy AC, BD, MN đồng quy.

c) Ta có $PQ \bot BD\left( {gt} \right)$.

Xét các tam giác vuông POM và QOD có:

$\widehat {POB} = \widehat {QOD}$ (đối đỉnh), OB = OD và $\widehat {POB} = \widehat {QDO}$ (so le trong).

Do đó $\Delta POB = \Delta QOD\left( {g.c.g} \right)$

$\Rightarrow BP = DQ$

Lại có $BP\parallel DQ$ nên tứ giác PBQD là hình bình hành có hai đường chéo vuông góc nên là hình thoi.

d) Gọi F là giao điểm của BK và QC. Ta có O là trung điểm của BD và $OQ\parallel BD\left( {gt} \right)$ nên OQ là đường trung bình của $\Delta DBF \Rightarrow Q$ là trung điểm của DF.

Lại có $QK\parallel BD\left( {gt} \right)$ nên QK là đường trung bình của $\Delta BDF \Rightarrow K$ là trung điểm của BF.

Mặt khác $\Delta BCF$ vuông tại C có CK là đường trung tuyến nên:

$CK = BK = {1 \over 2}BF.$

Xét $\Delta DBQ$ có đường cao QD đồng thời là đường trung tuyến nên $\Delta DBQ$ cân tại \Q \) $\Rightarrow QB = QD$ và QD = QF (cmt)

Vậy QD = OB = QF. Do đó $\Delta DBF$ vuông tại B.

Xét $\Delta OCK$ và $\Delta OBK$ có CK chung

OC = OB (tính chất đường chéo hình chữ nhật)

CK = BK (cmt)

Vậy $\Delta OCK = \Delta OBK\left( {c.c.c} \right)$

$\Rightarrow \widehat {OCK} = \widehat {OBK} = {90^ \circ }$ hay $AC \bot CK.$

HocTot.Nam.Name.Vn