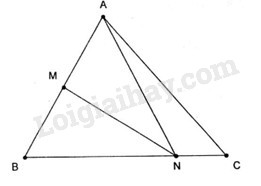
Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Hình học 10Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Hình học 10 Đề bài Câu 1.Cho hình vuông ABCD cạnh bằng a, M là điểm bất kì. a.Chứng minh véc tơ →v=4→MA−→MB−2→MC−→MD không phụ thuộc vào M. b.Tính độ dài của →v . Câu 2.Cho tam giác ABC có M là trung điểm AB và N là điểm trên đoạn BC sao cho BN= 3NC. a. Chứng minh rằng →AN=14→AB+34→AC . b. Hãy biểu thị véc tơ →MN theo các véc tơ →AB và →AC . Câu 3. Cho tam giác ABC. Tìm tập hợp điểm M sao cho |2(→MA+→MB+→MC)|=|3(→MB+→MC)| . Câu 4. Trong mặt phẳng tọa độ Oxy cho hai điểm A(-4;3) và B(2;-5). a. Tìm tọa độ điểm A’ đối xứng với A qua B. b. Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng. Lời giải chi tiết Câu 1. a.Ta có →v=4→MA−→MB−2→MC−→MD =(→MA−→MB)+(2→MA−2→MC)+(→MA−→MD) =→BA+2→CA+→DA =−→AB−2→AC−→AD =−(→AB+→AD+2→AC) =−(→AC+2→AC)=−3→AC =3→CA Vậy →v không phụ thuộc vào M. b. Tam giác ABC vuông tại B nên theo Pitago ta có: AC=√AB2+BC2=√a2+a2=a√2 |→v|=|3→CA|=3CA=3a√2 Câu 2.
a.Ta có: →NB=−3→NC ⇔→AB−→AN=−3(→AC−→AN) ⇔→AB−→AN=−3→AC+3→AN⇔→AB+3→AC=4→AN ⇔4→AN=→AB+3→AC ⇔→AN=14→AB+34→AC b.Ta có →MN=→AN−→AM =14→AB+34→AC−12→AB =−14→AB+34→AC Câu 3.
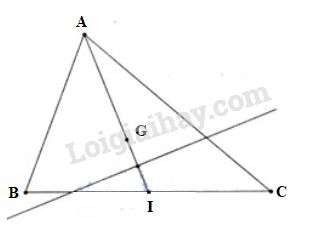
Gọi G là trọng tâm tam giác ABC, I là trung điểm BC. Ta có: |2(→MA+→MB+→MC)|=|3(→MB+→MC)| ⇔|6→MG|=|6→MI|⇔MG=MI M cách đều hai điểm cố định G và I nên tập hợp các điểm M là đường trung trực của đoạn GI. Câu 4. a. A(−4;3) và B(2;−5). A′ đối xứng với A qua B khi và chỉ khi B là trung điểm của đoạn AA′ . Do đó {xB=xA+xA′2yB=yA+yA′2 ⇔{xA′=2xB−xA=8yA′=2yB−yA=−13 Vậy A′=(8;−13) . b.Gọi M(xM;0) là điểm trên trục hoành. Ta có →AM=(xM+4;−3),→AB=(6;−8) . M, A, B thẳng hàng khi và chỉ khi →AM và →AB cùng phương xM+46=−3−8 ⇔4xM+16=9 ⇔xM=−74 Vậy M=(−74;0) . HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|
