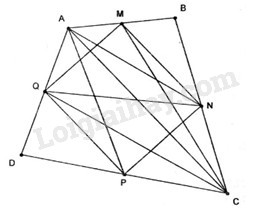
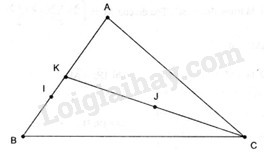
Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 1 - Hình học 10

Đề bài

Câu 1. Cho tứ giác lồi ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Chứng minh rằng

a.Chứng minh rằng \(\overrightarrow {MP}  = \dfrac{1 }{ 2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right)\) .

b.Hai tam giác ANP và CMQ có cùng trọng tâm.

Câu 2. Cho tam giác ABC. Xác định các điểm I, J sao cho

\(\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 ,\)\(\,\overrightarrow {JA}  + \overrightarrow {JB}  + 2\overrightarrow {JC}  = \overrightarrow 0 \) .

Câu 3. Cho hai điểm cố định A, B. Tìm tập hợp các điểm M sao cho

\(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  - \overrightarrow {MB} } \right|\) .

Câu 4. Trong mặt phẳng tọa độ Oxy cho ba điểm \(A(1;2), B(-3;-2), C(5;-1).\)

A.Chứng minh A, B, C là ba đỉnh của một tam giác.

b.Tìm tọa độ của véc tơ trung tuyến \(\overrightarrow {AM} \) của tam giác ABC.

c.Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

Lời giải chi tiết

Câu 1.

a. \(\dfrac{1 }{2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right) \)

\(= \dfrac{1 }{ 2}\left( {\overrightarrow {AM}  + \overrightarrow {MP}  + \overrightarrow {PD}  + \overrightarrow {BM}  + \overrightarrow {MP}  + \overrightarrow {PC} } \right)\)

\( = \dfrac{1 }{ 2}\left( {2\overrightarrow {MP}  + \overrightarrow {AM}  + \overrightarrow {BM}  + \overrightarrow {PC}  + \overrightarrow {PD} } \right)\)

\(= \overrightarrow {MP} \)

b. Theo tính chất đường trung bình \(\overrightarrow {NM}  = -\dfrac{1}{ 2}\overrightarrow {AC} ,\overrightarrow {PQ}  =- \dfrac{1 }{2}\overrightarrow {AC} \) .

Gọi G là trọng tâm tam giác ANP. Ta có \(\overrightarrow {GA}  + \overrightarrow {GN}  + \overrightarrow {GP}  = \overrightarrow 0 \) .

Suy ra:

\(\overrightarrow {GC}  + \overrightarrow {GM}  + \overrightarrow {GQ}  \)

\(= \overrightarrow {GA}  + \overrightarrow {AC}  + \overrightarrow {GN}  + \overrightarrow {NM}  + \overrightarrow {GP}  + \overrightarrow {PQ} \)

\( = \overrightarrow {GA}  + \overrightarrow {GN}  + \overrightarrow {GP} \) \( + \overrightarrow {AC}  - \dfrac{1 }{ 2}\overrightarrow {AC}  - \dfrac{1 }{ 2}\overrightarrow {AC}  = \overrightarrow 0 \)

Vậy G là trọng tâm tam giác CMQ.

Câu 2.

Ta có:

\(\eqalign{  & \overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 \cr& \Leftrightarrow \overrightarrow {IA}  + 2\left( {\overrightarrow {IA}  + \overrightarrow {AB} } \right) = \overrightarrow 0   \cr  & {\rm{                   }} \Leftrightarrow 3\overrightarrow {IA}  + 2\overrightarrow {AB} =\overrightarrow 0   \cr} \)

\(\begin{array}{l}
\Leftrightarrow 3\overrightarrow {IA} = - 2\overrightarrow {AB} \\
\Leftrightarrow - 3\overrightarrow {IA} = 2\overrightarrow {AB} \\
\Leftrightarrow 3\overrightarrow {AI} = 2\overrightarrow {AB}
\end{array}\)

\(\Leftrightarrow \overrightarrow {AI}  = {2 \over 3}\overrightarrow {AB}\)

Suy ra I là điểm trên cạnh AB sao cho \(AI = \dfrac{2 }{ 3}AB\).

Gọi K là trung điểm AB. Ta có

\(\overrightarrow {JA}  + \overrightarrow {JB}  + 2\overrightarrow {JC}  = \overrightarrow 0\)

\(  \Leftrightarrow 2\overrightarrow {JK}  + 2\overrightarrow {JC}  = \overrightarrow 0 \)

\(\Leftrightarrow \overrightarrow {JK}  + \overrightarrow {JC}  = \overrightarrow 0 \)

Suy ra J là trung điểm KC.

Câu 3.

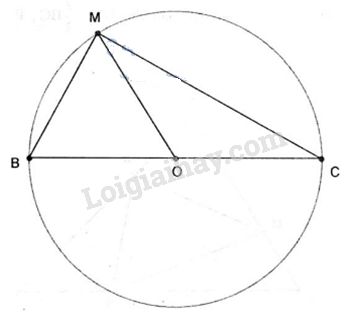
Gọi O là trung điểm AB.

Ta có: \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  - \overrightarrow {MB} } \right| \)

\(\Leftrightarrow \left| {2\overrightarrow {MO} } \right| = \left| {\overrightarrow {BA} } \right|\)

\(\Leftrightarrow MO = \dfrac{1 }{ 2}AB\) .

M cách O cố định một đoạn không đổi bằng \(\dfrac{1 }{ 2}AB\) nên tập hợp các điểm M là đường trong tâm O bán kính \(\dfrac{1 }{2}AB\) hay có đường kính là AB.

Câu 4.

a.Ta có \(\overrightarrow {AB}  = \left( { - 4; - 4} \right),\overrightarrow {AC}  = \left( {4; - 3} \right)\) .

Mà \(\dfrac{{ - 4}}{{ - 4}} \ne \dfrac{{ - 4}}{{ - 3}}\) . Suy ra \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương.

Vậy A, B, C không thẳng hàng hay A, B, C là ba đỉnh của một tam giác.

b.Gọi M là trung điểm BC.

Tọa độ của M là \(\left( {\dfrac{{{x_B} + {x_C}}}{2};\dfrac{{{y_B} + {y_C}}}{2}} \right) = \left( {1; - \dfrac{3}{2}} \right).\)

Suy ra \(\overrightarrow {AM}  = \left( {0; - {7 \over 2}} \right)\) .

c. ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC}  = \overrightarrow {AB} \) .

Mà \(\overrightarrow {DC}  = \left( {5 - {x_D}; - 1 - {y_D}} \right),\)\(\,\overrightarrow {AB}  = \left( { - 4, - 4} \right)\) .

Do đó \(\left\{ \matrix{  5 - {x_D} =  - 4 \hfill \cr   - 1 - {y_D} =  - 4 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_D} = 9 \hfill \cr  {y_D} = 3 \hfill \cr}  \right.\) .

 Vậy \(D = \left( {9;3} \right)\) .

 HocTot.Nam.Name.Vn