Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 3 - Hình học 7

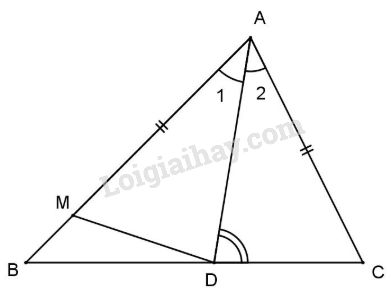
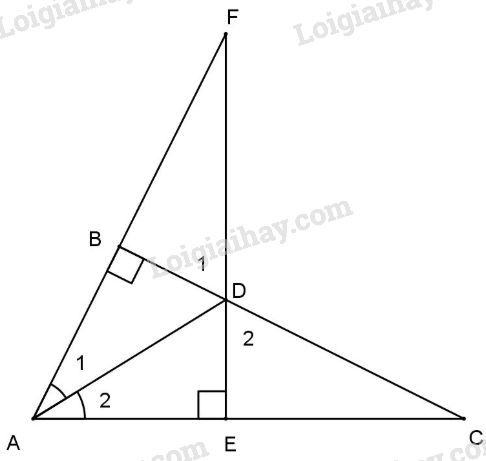
Đề bài

Bài 1: Tìm chu vi của một tam giác cân biết hai cạnh tron ba cạnh của tam giác có độ dài là 4cm; 9cm.

Bài 2: Cho tam giác ABC ($AB > AC$). Gọi AD là phân giác của góc A. Trên tia AB lấy điểm M sao cho AM = AC. Chứng minh:

a) $\Delta A{\rm{D}}M = \Delta ADC.$ 

b) $\widehat {A{\rm{D}}B} > \widehat {A{\rm{D}}C}.$

Bài 3: Cho tam giác ABC vuông tại B, vẽ phân giác AD (D thuộc BC). Từ D vẽ  DE vuông góc với AC (E thuộc AC).

a) Chứng minh rằng: BD = DE.

b) Chứng minh: $C{\rm{D}} > B{\rm{D}}.$

e) ED cắt AB tại F. Chứng minh $\Delta A{\rm{D}}F = \Delta A{\rm{D}}C.$

d) Chứng minh $BA + BC > DE + AC.$

LG bài 1

Phương pháp giải:

+Trong một tam giác độ dài 1 cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại

Lời giải chi tiết:

Bài 1: Cạnh bên của tam giác cân đã cho không thể bằng 4, 
vì $4 + 4 < 9,$ trái với bất đảng thức tam giác nên cạnh bên phải là 9,
vì $9 + 9 > 4.$ Do đó chu vi tam giác cân là $2.9 + 4 = 22$ (cm).

LG bài 2

Phương pháp giải:

+ Trong 1 tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn

+Tổng ba góc của 1 tam giác bằng 180 độ

Lời giải chi tiết:

a) Xét $\Delta A{\rm{D}}M$ và $\Delta A{\rm{D}}C$ có:

+) AD cạnh chung

+) ${\widehat A_1} = {\widehat A_2}$ (gt);

+) $AM = AC$ (gt).

Do đó $\Delta A{\rm{D}}M = \Delta A{\rm{D}}C$ (c.g.c)

b) Vì $AB > AC$ (gt) $\Rightarrow \widehat B < \widehat C$.

Xét $\Delta A{\rm{D}}B$ ta có $\widehat {A{\rm{D}}C} + \widehat C + {\widehat A_2} = {180^0}.$ 

Tương tự $\Delta A{\rm{D}}C$ ta có $\widehat {A{\rm{D}}C} + \widehat C + {\widehat A_2} = {180^0},$ 
mà ${\widehat A_1} = {\widehat A_2}$ (gt); $\widehat B < \widehat C$ (cmt)

$\Rightarrow \widehat {ADB} > \widehat {ADC}$ (cmt).

LG bài 3

Phương pháp giải:

+Trong tam giác vuông cạnh góc vuông nhỏ hơn cạnh huyền

+Hai góc đối đỉnh thì bằng nhau

Lời giải chi tiết:

a) Xét hai tam giác vuông ABD và AED có :

+) AD cạnh chung;

+) ${\widehat A_1} = {\widehat A_2}$ (gt).

Do đó $\Delta AB{\rm{D}} = \Delta A{\rm{ED}}$ (ch.gn)

$\Rightarrow B{\rm{D}} = DE$ (cạnh tương ứng).

b) Xét tam giác vuông DEC ta có $DE < DC$ (cgv<ch), mà DE = DB (cmt)

$\Rightarrow C{\rm{D}} > DB$ .

c) Xét hai tam giác vuông DBF và DEC có:

+) ${\widehat D_1} = {\widehat D_2}$ (đối đỉnh);

+) $DB = DE$ (cmt).

Do đó $\Delta DBF = \Delta DEC$ (g.c.g)

$\Rightarrow BF = EC$ 

Lại có $BA = E{\rm{A}}$ (cmt)

$\Rightarrow BF + BA = EC + E{\rm{A}}$ 

hay $AF = AC.$                                

Xét $\Delta A{\rm{D}}F$ và $\Delta A{\rm{D}}C$ có:

+) AD cạnh chung;

+) ${\widehat A_1} = {\widehat A_2}$ (gt);
+) AF = AC (cmt)

$\Delta A{\rm{D}}F = \Delta A{\rm{D}}C$ (c.g.c).

d) Ta có vế trái: $BA + BC = A{\rm{E}} + B{\rm{D}} + DC$ (vì $BA = A{\rm{E}}$ cmt).

Vế phải: $DE + AC = DB + A{\rm{E}} + EC$ (vì DE = DB theo cmt).

Trong tam giác vuông DEC ta có $DC > EC$ (ch-cgv).

Vậy   $A{\rm{E}} + B{\rm{D}} + DC > DB + A{\rm{E}} + EC$ hay $BA + BC > DE + AC.$

HocTot.Nam.Name.Vn