Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 2 - Hình học 7

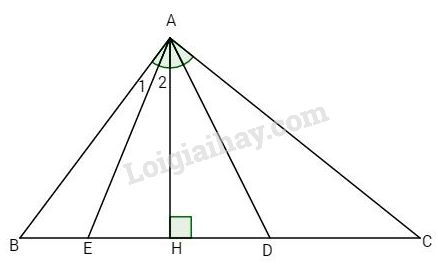
Đề bài

Bài 1. Cho biết $\Rightarrow \widehat {{A_1}} + \widehat {BAD} + \widehat {{A_3}} = {90^o}$ $\Delta ABC = \Delta HIK$, trong đó có $AC = 5cm$, $\widehat A = {70^o},\,\widehat C = {50^o}$. Tính HK và số đo góc I của tam giác HIK.

Bài 2. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC. Tia phân giác của góc $\widehat {HAB}$ cắt BC tại E, tia phân giác của góc $\widehat {HAC}$ cắt BC tại D. Chứng minh rằng $AB + AC = BC + DE.$

Bài 3. Cho tam giác ABC có ba góc nhọn, kẻ BD vuông góc với AC (D thuộc AC) và CE vuông góc với AB (E thuộc AB). Trên tia đối của tia BD lấy điểm F sao cho $BF = AC$. Trên tia đối của tia CE lấy điểm G sao cho $CG = AB.$

a) Chứng minh $\widehat {ABF} = \widehat {ACG}$.

b) Chứng minh $AF = AG$ và $AF \bot AG.$

LG bài 1

Phương pháp giải:

Sử dụng:

Tính chất 2 tam giác bằng nhau

Tổng ba góc của 1 tam giác bằng 180 độ

Lời giải chi tiết:

$\Delta ABC = \Delta HIK$(giả thiết) $\Rightarrow HK = AC = 5cm.$

$\widehat {HIK} = \widehat {ABC} = {180^o} - \left( {\widehat A + \widehat C} \right)$$\;= {180^o} - \left( {{{70}^o} + {{50}^o}} \right) = {60^o}$.

$\widehat {AEC} = \widehat {{A_2}} + \widehat {HAC}$, mà $\widehat {{A_1}} = \widehat {{A_2}}$ (giả thiết)

LG bài 2

Phương pháp giải:

Sử dụng:

Hai góc cùng phụ với góc thứ 3 thì bằng nhau

Góc ngoài của tam giác bằng tổng 2 góc trong không kề với nó

Tổng ba góc của 1 tam giác bằng 180 độ

Tam giác cân có 2 cạnh bên bằng nhau

Lời giải chi tiết:

Ta có $\widehat {AEH} = \widehat B + \widehat {{A_1}}$ (góc ngoài của $\Delta AEB$

$\widehat B = \widehat {HAC}$ (cùng phụ với góc C)

$\Rightarrow \widehat {AEC} = \widehat {EAC} \Rightarrow \Delta AEC$ cân tại C

$\Rightarrow AC = EC.$

Chứng minh tương tự ta lại có $\Delta ABD$ cân tại B $\Rightarrow AB = BD.$

Từ đó vế trái: $AB + AC = BD + CE$$\;= BD + ED + DC;$

Vế phải: $BC + DE = BD + DC + DE.$

Vậy $AB + AC = BC + DE\,(đpcm)$.

LG bài 3

Phương pháp giải:

Sử dụng:

Hai góc cùng phụ với góc thứ 3 thì bằng nhau

Tổng 2 góc kề bù bằng 180 độ

Lời giải chi tiết:

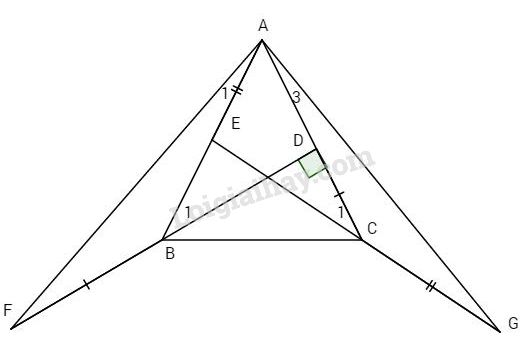
a) Ta có $\widehat {{B_1}} = \widehat {{C_1}}$ (cùng phụ với góc $\widehat {BAC}$), mà $\widehat {{B_1}} + \widehat {ABF} = {180^o}$ (kề bù).

Tương tự $\widehat {{C_1}} + \widehat {ACG} = {180^o} \Rightarrow \widehat {ABF} = \widehat {ACG}.$

b) Xét $\Delta ABF$ và $\Delta GCA$ có

+) $AB = CG$ (giả thiết)

+) $\widehat {ABF} = \widehat {ACG}$ (chứng minh trên)

+) $BF = AC$ (giả thiết).

Do đó $\Delta ABF = \Delta GCA$(c.g.c)

$\Rightarrow AF = AG.$

Ta có $\Delta ADF$ vuông tại D (giả thiết) nên $\widehat {{A_1}} + \widehat {BAD} + \widehat F = {90^o}$

Mà $\widehat F = \widehat {{A_3}}\,(\Delta ABF = \Delta GCA)$

$\Rightarrow \widehat {{A_1}} + \widehat {BAD} + \widehat {{A_3}} = {90^o}$ hay $AF \bot AG.$

HocTot.Nam.Name.Vn