Đề kiểm tra 45 phút ( 1 tiết) - Đề số 3 - Chương 1 - Hình học 8

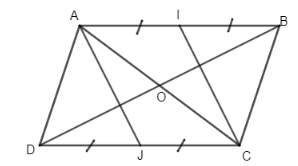
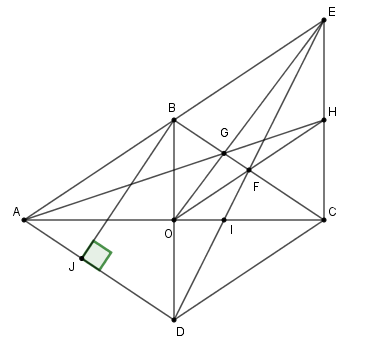
Đề bài

Bài 1. Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD, I là trung điểm của cạnh AB, J là trung điểm của DC.

a) Chứng tỏ AJ = CI. 

b) Chứng tỏ O là trung điểm của đoạn IJ.

Bài 2. Cho hình thoi ABCD có hai dường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC tại I và BC ở F.

a) Chứng minh ID = 2IF.

b) Nối EO cắt BC ở G, đường thẳng OF cắt EC ở H. Chứng minh ba điểm A, G, H thẳng hàng.

c) Biết \(\widehat {BAD} = {60^ \circ },AB = a.\) Tính diện tích hình thoi ABCD theo a.

LG bài 1

Phương pháp giải:

Sử dụng:

Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành

Lời giải chi tiết:

a) I, J lần lượt là trung điểm của AB và CD

\( \Rightarrow AI\parallel CJ\) và AI = CJ.

Do đó tứ giác AICJ là hình bình hành

\( \Rightarrow {\rm{AJ}} = CI.\)

b) O là giao điểm hai đường chéo AC và BD nên O là trung điểm của AC. AICJ là hình bình hành (cmt). Do đó đường chéo thứ hai IJ phải qua O hay O là trung điểm của IJ.

LG bài 2

Phương pháp giải:

Sử dụng:

Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành

Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương các cạnh góc vuông

Lời giải chi tiết:

a) Ta có  BE = BA (gt) mà \(BA\parallel CD\) và BA = CD (gt)

\( \Rightarrow BE\parallel CD\) và \(BE = CD.\)

Do đó BECD là hình bình hành nên F là trung điểm của BC.

Xét \(\Delta BDC\) có I là trọng tâm \( \Rightarrow ID = 2IF.\)

b) Ta có OF là đường trung bình của \(\Delta BDC \Rightarrow OF\parallel DC\)

Mà \(DC\parallel AB\) nên \(OF\parallel AE.\) 

Vì O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của \(\Delta AEC\). Mà AH cắt EO tại G nên G là trọng tâm \(\Delta AEC \Rightarrow A,G,H\) thẳng hàng.

c) \(\Delta ABD\) cân (AB = AD (gt) có\(\widehat {BAD} = {60^ \circ }\) nên \(\Delta ABD\) đều.

Kẻ \(BJ \bot AD\) ta có: \(JA = JD = {{AD} \over 2} = {a \over 2}\)

\( \Rightarrow BJ = \sqrt {A{B^2} - A{J^2}}  \)\(\;= \sqrt {{a^2} - {{\left( {{a \over 2}} \right)}^2}}  = \sqrt {{{3{a^2}} \over 4}}  = {{a\sqrt 3 } \over 2}.\)

Vậy \({S_{ABCD}} = AD.BJ = a.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 2}.\)

HocTot.Nam.Name.Vn