Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 2 - Hình học 10Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 2 - Hình học 10 Đề bài Câu 1 (2đ) Cho hình chữ nhật ABCD, AB=3;AD=4 Hãy tính? a. |→AB+→AD| b. |2→AB+3→AD| Câu 2 (1đ) Cho ΔABC có đường trung tuyến AM. Gọi I là trung điểm của AM. Chứng minh các đẳng thức vectơ sau: a) →AB+→CI=→AI+→CB b) 2→IA+→IB+→IC=→0 Câu 3 (2đ) Cho các véc tơ : →a=(2;−3) , →b=(−5;1) và →c=(−5;−12). a) Tính toạ độ véc tơ →u=→2a+3→b . b) Phân tích vectơ →c theo hai vectơ →a và →b. Câu 4 (2.5đ) Trong mặt phẳng tọa độ Oxy, cho ba điểm A(4;1); B(0;3); C(1;2). a) Chứng minh ba điểm A, B, C lập thành ba đỉnh của một tam giác. b) Tìm tọa độ của trung điểm cạnh AB. c) Tìm tọa độ trọng tâm G của tam giác ABC. d) Tìm tọa độ điểm D của hình bình hành ABCD. e) Tìm tọa độ điểm E thuộc trục hoành sao cho AE+BE đạt giá trị nhỏ nhất. Câu 5 (1đ) Cho hình bình hành ABCD. Gọi M là trung điểm của AB. a. Tính →DM theo →DA và →DC; b. Gọi N là điểm thỏa mãn →NC+2→NA=→0. Chứng minh D, N, M thẳng hàng. Câu 6 (0.75đ) Cho tam giác ABC.Tìm tập hợp các điểm M thỏa mãn |→MA+→MB+→MC|=32|→MB+→MC| Câu 7 (0.75đ) Biết tháp Eiffel ở thủ đô Paris nước Pháp có chiều cao là 324m. Khi xây dựng người ta thiết kế theo tỉ lệ vàng. Tính độ cao từ mặt đất tới tầng 2 của tháp (Đoạn AB)
Lời giải chi tiết Câu 1 (2 điểm)
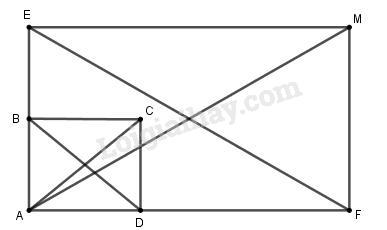
a) Ta có: ABCD là hình chữ nhật nên |→AB+→AD|=|→AC|=AC Tam giác ABC vuông tại B nên theo Pitago ta có: AC=√AB2+BC2 =√32+42=5 Vậy |→AB+→AD|=5. b) Dựng các điểm E, F sao cho →AE=2→AB;→AF=3→AD ⇒AE=2AB=2.3=6AF=3AD=3.4=12 Dựng hình chữ nhật AEMF ta có : |2→AB+3→AD|=|→AE+→AF|=|→AM|=AM Tam giác AEM vuông tại E nên theo Pitago ta có: AM=√AE2+EM2=√62+122=6√5 Câu 2 (1 điểm)
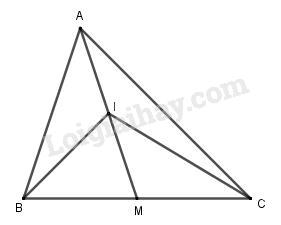
a. →AB+→CI=→AI+→CB⇔(→AB−→AI)+→CI−→CB=→0⇔→CI+→IB−→CB=→0⇔→CB−→CB=→0 b. 2→IA+→IB+→IC=→0⇔2→IA+2→IM=→0 ⇔2(→IA+→IM)=→0 (đúng vì I là trung điểm của AM) (đpcm) Câu 3 (2 điểm) →a=(2;−3) , →b=(−5;1) và →c=(−5;−12) a. 2→a=(4;−6)3→b=(−15;3) →u=→2a+3→b=(−11;−3) b. Gọi hai số m, n thoã mãn →c=m→a+n→b Ta có hệ phương trình :{2m−5n=−5−3m+n=−12⇔{m=5n=3 Vậy : →c=5→a+3→b Câu 4 (2.5 điểm) A(4;1); B(0;3); C(1;2). a. →AB=(−4;2);→AC=(−3;1) Ta có −4−3≠21 nên →AB,→AC không cùng phương. Vậy A, B, C là 3 đỉnh của tam giác. b. Gọi M là trung điểm của AB thì {xM=xA+xB2=4+02=2yM=yA+yB2=1+32=2 ⇒M(2;2) Vậy tọa độ trung điểm của AB là :M(2;2) c. Gọi G là trọng tâm tam giác ABC thì: {xG=4+0+13=53yG=1+3+23=2 ⇒G(53;2) Vậy tọa độ trọng tâm G của tam giác ABC: G(53;2) d. →BC=(1;−1) ABCD là hình bình hành ⇔→AD=→BC⇔{xD−4=1yD−1=−1⇔{xD=5yD=0 Vậy D(5;0) e.
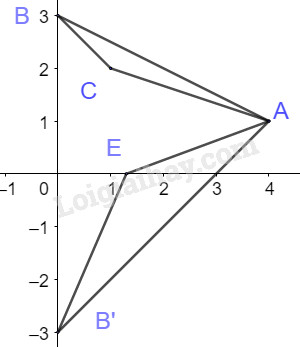
Gọi E(xE;0)∈Ox Gọi B’ đối xứng với B qua trục Ox thì B′(0;−3) AE+BE=AE+B′E≥AB′ Do đó AE+BE đạt GTNN bằng AB′ khi A,B’,E thẳng hàng ⇔→AE=k→AB′⇔{xE−4=−4k0−1=k.(−4) ⇔{k=14xE=3 Vậy E(3;0) Câu 5 (1 điểm)
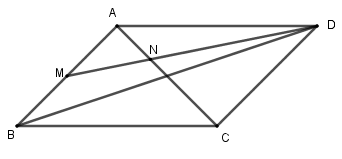
a. →DM=12(→DA+→DB)=12(→DA+→DA+→DC) =12(2→DA+→DC)=→DA+12→DC (1) b. →NC+2→NA=→0 ⇔→DC−→DN+2(→DA−→DN)=→0⇔→DC−→DN+2→DA−2→DN=→0⇔3→DN=2→DA+→DC⇔32→DN=→DA+12→DC(2) Từ (1) và (2) suy ra: →DM=32→DN nên 3 điểm D, M, N thẳng hàng. Câu 6 (0.75 điểm) Gọi G là trọng tâm tam giác ABC, I là trung điểm BC. Khi đó →MA+→MB+→MC=3→MG→MB+→MC=2→MI |→MA+→MB+→MC|=32|→MB+→MC|⇔|3→MG|=32|2→MI|⇔3|→MG|=3|→MI|⇔MG=MI Vậy tập hợp các điểm M là đường trung trực của đoạn GI. Câu 7 (0.75 điểm) Do xây theo tỉ lệ vàng nên ta có BCAB=1,618⇒BC=1,618AB Mà BC+AB=324 nên 1,618AB+AB=324 ⇔2,618AB=324 ⇔AB=123,76 Vậy độ cao của tháp là 123,76(m). Sưu tầm HocTot.Nam.Name.Vn
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|