Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 3 - Hình học 11

Đề bài

Câu 1. Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\), SD = 2a. Gọi \(\alpha \) là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau ?

A. \(\cos \alpha  = \dfrac{{\sqrt 6 }}{2}\). 

B. \(\tan \alpha  = \dfrac{{\sqrt 6 }}{2}\).

C. \(\cos \alpha  = \dfrac{{\sqrt 6 }}{3}\).      

D. \(\tan \alpha  = \dfrac{{\sqrt 6 }}{3}\)

Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SO vuông góc với mặt phẳng (ABCD). Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng:

A. \(\widehat {SAB}\).                    B. \(\widehat {SBA}\).

C. \(\widehat {SOB}\).                    D. \(\widehat {SBO}\).

Câu 3. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, I là trung điểm của đoạn MN. Đẳng thức nào sau đây sai?

A. \(\overrightarrow {AB}  + \overrightarrow {DC}  = \overrightarrow {AD}  + \overrightarrow {BC} \).        

B. \(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  = \overrightarrow {AD} \).

C. \(\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {DC} } \right)\). 

D. \(\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  + \overrightarrow {ID}  = \overrightarrow 0 \).

Câu 4. Trong các mệnh đề sau, mệnh đề nào sai?

A. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.

B. Một đường thẳng vuông góc với hai cạnh của một tam giác thì cũng vuông góc với cạnh còn lại.

C. Mặt phẳng trung trực của một đoạn thẳng là mặt phẳng vuông góc với đoạn thẳng đó tại trung điểm.

D. Tồn tại duy nhất một đường thẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.

Câu 5. Cho hình hộp ABCD.A’B’C’D’. Giả sử tam giác AB’C và A’DC’ đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A’D là góc nào sau đây ?

A. \(\widehat {AB'C}\).               B. \(\widehat {DA'C'}\).

C. \(\widehat {BB'D}\).               D. \(\widehat {BDB'}\).

Câu 6. Trong không gian cho hai đường thẳng a và b vuông góc với nhau. Tìm mệnh đề đúng.

A. a và b chéo nhau.        

B. a và b cắt nhau.

C. a  và b cùng thuộc một mặt phẳng.  

D. Góc giữa a và b bằng 90⁰.

Câu 7. Cho tứ diện ABCD. Gọi E là trung điểm AD, F là trung điểm BC và G là trọng tâm của tam giác BCD. Tìm mệnh đề sai trong các mệnh đề sau:

A. \(\overrightarrow {EB}  + \overrightarrow {EC}  + \overrightarrow {ED}  = 3\overrightarrow {EG} \).

B. \(2\overrightarrow {EF}  = \overrightarrow {AB}  + \overrightarrow {DC} \).

C. \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 3\overrightarrow {AG} \). 

D. \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \).

Câu 8. Cho ba vec tơ \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \). Điều kiện nào sau đây không kết luận được ba vec tơ đó đồng phẳng?

A. Một trong ba vec tơ đó bằng \(\overrightarrow 0 \).

B. Có hai trong ba vec tơ đó cùng phương.

C. Có một vec tơ không cùng hướng với hai vec tơ còn lại.

D. Có hai trong ba vec tơ đó cùng phương.

Câu 9. Khẳng định nào sau đây đúng?

A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

B. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

C. Hai đường thẳng cùng song song với đường thẳng thú ba thì song song với nhau.

D. Hai đường thẳng cùng song song với đường thẳng thứ ba thì vuông góc với nhau.

Câu 10. Cho tứ diện ABCD có BDC là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a. Góc giữa CM với mặt phẳng (BCD) là:

A.\(\widehat {BCM}\).             B. \(\widehat {DCM}\).

C. \(\widehat {KCM}\).            D. \(\widehat {ACM}\).

Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a. Mặt phẳng (ABCD) vuông góc với mặt phẳng ;

A. (SAD).                 B. (SBD).

C. (SDC).                 D. (SBC).

Câu 12. Cho chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Đường thẳng SA vuông góc  với :

A. SC.               B. SB.

C. SD.               D. CD

Câu 13. Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AB và CD. Ta có:

\(A.\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right) +\dfrac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {DB} } \right)\)

B. \(\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {AD}  - \overrightarrow {BC} } \right)\).

C. \(\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {AC}  - \overrightarrow {BD} } \right)\).

\(D. \overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right) - \dfrac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right).\)

Câu 14. Cho hình hộp ABCD. A’B’C’D’ có tất cả các cạnh bằng a và các góc phẳng đỉnh B đều bằng 60⁰. Cặp đường thẳng nào sau đây không vuông góc với nhau?

A. B’C và AD’.           B. BC’ và A’D.

C. B’C và CD’.           D. AC và B’D’.

Câu 15. Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc . Đường thẳng DE vuông góc với:

A. Chỉ với AC.        

B. Chỉ với BF.

C. Chỉ với AC và BF. 

D. Hoặc với AC hoặc với BF.

Câu 16. Cho tứ diện ABCD . Đặt \(\overrightarrow {AB}  = \overrightarrow b \,,\,\overrightarrow {AC}  = \,\overrightarrow c \,,\,\overrightarrow {AD}  = \overrightarrow d \). Gọi G là trọng tâm của tam giác BCD. Trong các đẵng thức sau, đẳng thức nào đúng ?

A. \(\overrightarrow {AG}  = \dfrac{1}{4}\left( {\overrightarrow b  + \overrightarrow c  + \overrightarrow d } \right)\). 

B. \(\overrightarrow {AG}  = \dfrac{1}{3}\left( {\overrightarrow b  + \overrightarrow c  + \overrightarrow d } \right)\).

C. \(\overrightarrow {AG}  = \dfrac{1}{2}\left( {\overrightarrow b  + \overrightarrow c  + \overrightarrow d } \right)\).    

D. \(\overrightarrow {AG}  = \overrightarrow d  + \overrightarrow c  + \overrightarrow b \).

Câu 17. Cho hình hộp ABCD.A₁B₁C₁D₁. Chọn khẳng định sai ?

A. \(\overrightarrow {BC}  + \overrightarrow {BA}  + \overrightarrow {B{B_1}}  = \overrightarrow {B{D_1}} \).  

B. \(\overrightarrow {BC}  + \overrightarrow {BA}  = \overrightarrow {{B_1}{C_1}}  + \overrightarrow {{B_1}{A_1}} \).

C. \(\overrightarrow {AD}  + \overrightarrow {{D_1}{C_1}}  + \overrightarrow {{D_1}{A_1}}  = \overrightarrow {DC} \).

D. \(\overrightarrow {BA}  + \overrightarrow {D{D_1}}  + \overrightarrow {B{D_1}}  = \overrightarrow {BC} \).

Câu 18. Trong không gian cho điểm O và bốn điểm A, B,C,D không thẳng hàng. Điều kiện cần và đủ để A, B,C,D tạo thành hình bình hành là:

A. \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0 \).

B. \(\overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB}  + \overrightarrow {OD} \).

C. \(\overrightarrow {OA}  + \dfrac{1}{2}\overrightarrow {OB}  = \overrightarrow {OC}  + \dfrac{1}{2}\overrightarrow {OD} \).  

D. \(\overrightarrow {OA}  + \dfrac{1}{2}\overrightarrow {OC}  = \overrightarrow {OB}  + \dfrac{1}{2}\overrightarrow {OD} \).

Câu 19. Cho hình hộp ABCD.A'B'C 'D' có tâmO. Đặt \(\overrightarrow {AB}  = \overrightarrow a \,,\,\overrightarrow {BC}  = \overrightarrow b \).M là điểm xác định bởi\(\overrightarrow {OM}  = \dfrac{1}{2}\left( {\overrightarrow a  - \overrightarrow b } \right)\). Khẳng định nào sau đây đúng?

A. M là tâm hình bình hành ABB' A'

B. M là tâm hình bình hành BCC 'B'

C. M là trung điểm BB'

D. M là trung điểm CC '.

Câu 20. Khẳng định nào sau đây sai?

A. Nếu đường thẳng \(d \bot \left( \alpha  \right)\) thì d vuông góc với hai đường thẳng trong \(\left( \alpha  \right)\).

B. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong \(\left( \alpha  \right)\)thì\(d \bot \left( \alpha  \right)\).

C. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong \(\left( \alpha  \right)\)thì d vuông

góc với bất kì đường thẳng nào nằm trong\(\left( \alpha  \right)\).

D. Nếu \(d \bot \left( \alpha  \right)\) và đường thẳng a //\(\left( \alpha  \right)\) thì \(d \bot a\).

Câu 21. Cho hình chóp S.ABCD có \(SA \bot \left( {ABC} \right)\) và đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD và I là trung điểm của SC . Khẳng định nào sau đây là khẳng định sai ?

A. \(BC \bot SB\)

B. \(\left( {SAC} \right)\)là mặt phẳng trung trực của đoạn BD.

C. \(IO \bot \left( {ABCD} \right)\).

D. Tam giác SCD vuông ở D.

Câu 22. Cho hình chóp S.ABCD , đáy ABCD là hình vuông có tâmO,\(SA \bot \left( {ABCD} \right)\). Gọi I là trung điểm của SC . Khẳng định nào sau đây là khẳng định sai ?

A. \(OI \bot \left( {ABCD} \right)\).

B. (SAC) là mặt phẳng trung trực của đoạn BD.

C. \(BD \bot SC\).

D. SA = SB = SC.

Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và\(SA \bot \left( {ABCD} \right)\). Khẳng định nào sau đây là khẳng định sai?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ABS.

B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc SOA  (O là tâm hình vuông ABCD ).

C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc SDA

D. \(\left( {SAC} \right) \bot \left( {SBD} \right)\)

Câu 24. Hình hộp ABCD.A'B'C 'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?

A. Tất cả các cạnh đáy bằng nhau và cạnh bên vuông góc với mặt đáy.

B. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc với mặt đáy

C. Có một mặt bên vuông góc với mặt đáy và đáy là hình vuông.

D. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông

Lời giải chi tiết

Câu	1	2	3	4	5
Đáp án	B	D	A	A	B
Câu	6	7	8	9	10
Đáp án	D	D	C	C	C
Câu	11	12	13	14	15
Đáp án	B	A	A	C	C
Câu	16	17	18	19	20
Đáp án	B	D	B	C	B
Câu	21	22	23	24
Đáp án	B	D	C	D

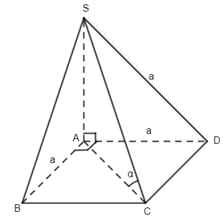
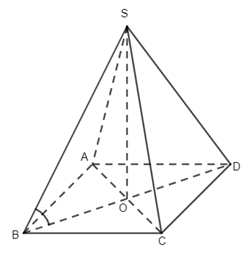
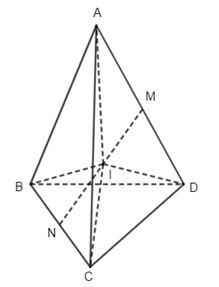
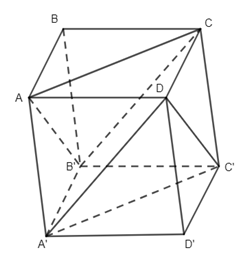
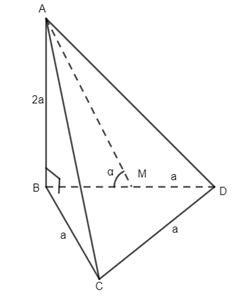
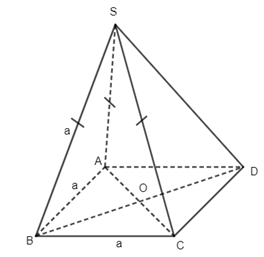
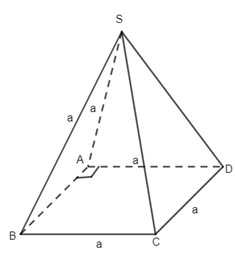
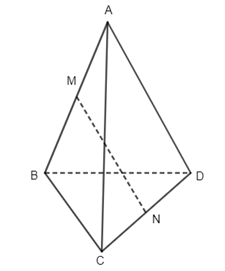
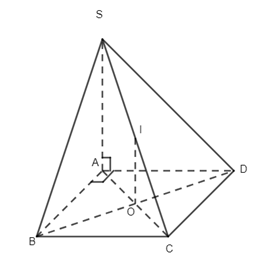
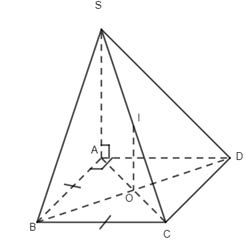
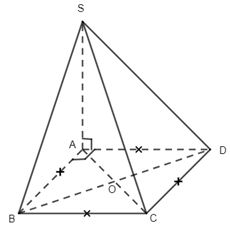
Câu 1.

 

Do \(SA \bot \left( {BACD} \right)\)  nên hình chiếu vuông góc của S lên (ABCD) là điểm A, suy ra \(\left( {SC,(ABCD)} \right) = \left( {SC,AC} \right)\)

Ta có

\(SA = \sqrt {4{a^2} - {a^2}}  = \sqrt 3 a\,,\,AC = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

\(\,\, \Rightarrow \tan \alpha  = \dfrac{{SA}}{{AC}} = \dfrac{{\sqrt 3 a}}{{a\sqrt 2 }} = \dfrac{{\sqrt 3 }}{{\sqrt 2 }} = \dfrac{{\sqrt 6 }}{2}\)

Chọn đáp án B.

Câu 2.

 

Do \(SO \bot \left( {ABCD} \right)\) ne6n hình chiếu vuông góc của S lân mp (ABCD) là điểm O, suy ra \(\left( {SB,(ABCD)} \right) = \left( {SB,\,BO} \right) = \widehat {SBO}\) .

Chọn đáp án D.

Câu 3.

 

Theo đề bài ta có I là trọng tâm tứ diện ABCD. Từ đó suy ra

\(\begin{array}{l}\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  + \overrightarrow {ID}  = \overrightarrow 0 \\\overrightarrow {MN}  = \overrightarrow {MI}  + \overrightarrow {IN}\\\;\;\;\;\;\;\;  =  - \dfrac{1}{2}\left( {\overrightarrow {IA}  + \overrightarrow {ID} } \right) + \dfrac{1}{2}\left( {\overrightarrow {IB}  + \overrightarrow {IC} } \right) \\\;\;\;\;\;\;\;= \dfrac{1}{2}\left( {\overrightarrow {IB}  - \overrightarrow {IA} } \right) + \dfrac{1}{2}\left( {\overrightarrow {IC}  - \overrightarrow {ID} } \right)\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {DC} } \right)\\\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  = \overrightarrow {IB}  - \overrightarrow {IA}  + \overrightarrow {IC}  - \overrightarrow {IB}  + \overrightarrow {ID}  - \overrightarrow {IC}  = \overrightarrow {ID}  - \overrightarrow {IA}  = \overrightarrow {AD} \end{array}\)

Chọn đáp án A.

Câu 5.

 

Do AC //A’C’ nên \(\left( {AC,A'D} \right) = \left( {A'C',\,A'D} \right)\). Do tam giác A’DC’ có ba góc nhọn nên \(\left( {A'C',A'D} \right) = \widehat {DA'C'}\) . Chọn đáp án B.

Câu 7.Do \(A\) không trùng với G nên \(\overrightarrow {GA}  \ne \overrightarrow 0 \). Mà do G là trọng tâm tam giác BCD nên \(\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GC}  = \overrightarrow 0 \). Từ đó suy ra \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  \ne \overrightarrow 0 \)

Chọn đáp án D.

Câu 10.

 

Do \(AB \bot (BCD)\,\,\)nên B là hình chiếu vuông góc của A lên (BCD), suy ra \(\left( {AM,(BCD)} \right) = \left( {AM,MB} \right) = \widehat {BMA}\,\, \Rightarrow \,\,\tan \alpha  = \dfrac{{AB}}{{BM}} = \dfrac{{2a}}{{\dfrac{a}{2}}} = 4\)

Chọn đáp án C.

Câu 11.

 

Ta có \(\left\{ \begin{array}{l}BD \bot AC\\SO \bot AC\end{array} \right.\,\, \Rightarrow \,\,AC \bot \left( {SBD} \right)\)mà \(AC \subset \left( {ABCD} \right)\)  nên \(\left( {SBD} \right) \bot \left( {ABCD} \right)\).

Chọn đáp án B.

Câu 12. Do tất cả các cạnh của hình chop đều bằng a nên tam giác SAC có \(AC = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 ,\,\,SA = a,\,SC = a\,\, \Rightarrow \,\,S{C^2} + S{A^2} = A{C^2}\) . Suy ra tam giác SAC vuông tại S hay \(SA \bot SC\) .

Chọn đáp án A.

Câu 13.

 

Ta có \(\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {MC}  + \overrightarrow {MD} } \right) = \dfrac{1}{2}\left( {\overrightarrow {BC}  + \overrightarrow {AC}  + \overrightarrow {AD}  + \overrightarrow {BD} } \right)\)

Chọn đáp án A.

Câu 14.

 

Đáp án C là đáp án đúng do tam giác CB’D’ có ba cạnh bằng nhau là \(a\sqrt 3 \)  nên không thể vuông tại C, tức là \(B'C \bot CD'\).

Câu 15.

 

\(\begin{array}{l}\left\{ \begin{array}{l}AC \bot DB\\AC \bot BE\,\,(\,(ABEF) \bot (ABCD)\, \Rightarrow BE \bot (ABCD))\end{array} \right. \Rightarrow AC \bot (BDE) \Rightarrow AC \bot DE\\\left\{ \begin{array}{l}FB \bot AE\\FB \bot AD\,\,((ABEF) \bot (ABCD) \Rightarrow AD \bot (ABEF))\end{array} \right.\, \Rightarrow FB \bot (ADE)\, \Rightarrow FB \bot DE\,\end{array}\)

Chọn đáp án C.

Câu 16. Do G là trọng tâm tam giác BCD nên \(3\overrightarrow {AG}  = \overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} \,\, \Rightarrow \overrightarrow {AG}  = \dfrac{1}{3}\left( {\overrightarrow b  + \overrightarrow c  + \overrightarrow d } \right)\)

Chọn đáp án B.

Câu 17.

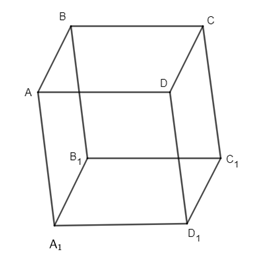
Ta có

 \(\begin{array}{l}\overrightarrow {BC}  + \overrightarrow {BA}  + \overrightarrow {B{B_1}}  = \overrightarrow {BD}  + \overrightarrow {B{B_1}}  = \overrightarrow {B{D_1}} \\\overrightarrow {BC}  + \overrightarrow {BA}  = \overrightarrow {BD}  = \overrightarrow {{B_1}{D_1}}  = \overrightarrow {{B_1}{A_1}}  + \overrightarrow {{B_1}{C_1}} \\\overrightarrow {AD}  + \overrightarrow {{D_1}{C_1}}  + \overrightarrow {{D_1}{A_1}}  = \overrightarrow {AD}  + \overrightarrow {DC}  + \overrightarrow {DA}  = \overrightarrow {DC} \\\overrightarrow {BA}  + \overrightarrow {D{D_1}}  + \overrightarrow {B{D_1}}  = \overrightarrow {BA}  + \overrightarrow {B{B_1}}  + \overrightarrow {B{D_1}}  = \overrightarrow {B{A_1}}  + \overrightarrow {B{D_1}}  \ne \overrightarrow {{A_1}{D_1}}  = \overrightarrow {BC} \end{array}\)

Chọn đáp án D.

Câu 18.

Với ABCD là hình bình hành, ta lấy I là giao điểm của hai đường chéo AC và BD.

Ta có \(\overrightarrow {OI}  = \dfrac{1}{2}\left( {\overrightarrow {OA}  + \overrightarrow {OC} } \right),\,\,\overrightarrow {OI}  = \dfrac{1}{2}\left( {\overrightarrow {OB}  + \overrightarrow {OD} } \right)\,\, \Rightarrow \overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB}  + \overrightarrow {OD} \) .

Ngược lại, với \(\overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB}  + \overrightarrow {OD} \). Lấy I’ là trung điểm AC, ta có \(\overrightarrow {OI'}  = \dfrac{1}{2}\left( {\overrightarrow {OA}  + \overrightarrow {OC} } \right) \Rightarrow OI' = \dfrac{1}{2}\left( {\overrightarrow {OB}  + \overrightarrow {OD} } \right)\) , suy ra I’ là trung điểm của BD.

Vậy ABCD là hình bình hành.

Chọn đáp án B.

Câu 19.

 

Ta có

\(\begin{array}{l}\dfrac{1}{2}\left( {\overrightarrow a  - \overrightarrow b } \right) = \dfrac{1}{2}\left( {\overrightarrow {AB}  - \overrightarrow {BC} } \right) = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {CB} } \right) = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {DA} } \right) = \dfrac{1}{2}\overrightarrow {DB} \\ \Rightarrow \overrightarrow {OM}  = \dfrac{1}{2}\overrightarrow {DB} \end{array}\)

Vậy M là trung điểm của BB’.

Chọn đáp án C.

Câu 21.

 

Ta có

\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\,\,(\,SA \bot (ABCD))\end{array} \right.\, \Rightarrow \,\,BC \bot (SAB)\, \Rightarrow BC \bot SB\\\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,\,(SA \bot (ABCD))\end{array} \right.\, \Rightarrow CD \bot (SAD)\,\, \Rightarrow CD \bot SD\end{array}\)

Do đó, tam giác SCD vuông tại D.

Do I, O là trung điểm của SC, AC nên OI // SA \( \Rightarrow \,\,OI \bot (ABCD)\).

ABCD là hình chữ nhật nên AC và BD không vuông góc với nhau, suy ra (SAC) không là mp trung trực của BD.

Chọn đáp án B.

Câu 22.

 

Ta có \(\left\{ \begin{array}{l}DB \bot AC\,\\DB \bot SA\end{array} \right.\, \Rightarrow BD \bot (SAC) \Rightarrow DB \bot SC\).

Do I, O là trung điểm của SC, AC nên OI // SA \( \Rightarrow \,\,OI \bot (ABCD)\).

ABCD là hình vuông nên AC và BD vuông góc với nhau mà O là tâm ABCD nên O là trung điểm của BD, tức là (SAC) là mp trung trực của đoạn BD.

Do tam giác SAB, SAC vuông tại A nên SA, SB, SC không bằng nhau.

Chọn đáp án D.

Câu 23.

 

Ta có

 \(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right.\,\, \Rightarrow BC \bot (SAB)\,\, \Rightarrow BC \bot SB\\BC \bot AB\end{array}\)

Lại có (SBC) và (ABCD) có BC chung , \(SB \subset (SBC),\,AB \subset (ABCD)\) suy ra \(\left( {(SBC),(ABCD)} \right) = \left( {AB,SA} \right) = \widehat {SBA}\)

Xét hai mp (ABCD) và (SBD) có BD chung, \(AO \bot BD,\,SO \bot BD\)  ( do \(\Delta SAB = \Delta SAD\, \Rightarrow SD = SB\)), suy ra  góc giữa ha imp (ABCD) và (SBD) là \(\widehat {SOA}\) .

\(SA \bot (ABCD),\,SA \subset (SAD)\)suy ra hai mp (ABCD ) và (SAD) vuông góc với nhau, khác \(\widehat {SDA}\) .

Chon đáp án C.

HocTot.Nam.Name.Vn