Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 3 – Đại số 7Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 3 – Đại số 7
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Bài 1: Trung bình cộng của sáu số là 4. Do thêm số thứ bảy nên trung bình cộng của bảy số là 5. Tìm số thứ bảy. Bài 2: Lỗi chính tả trong một bài tập làm văn của 40 học sinh được ghi lại ở bảng sau: (Biết rằng cả 40 em đều có bài kiểm tra và các bài có lỗi đều được thống kê ở bảng)
a) Tính số lỗi trung bình của mỗi bài kiểm tra. b) Tìm mốt của dấu hiệu. Tìm đơn vị điều tra. c) Có bao nhiêu bài viết không có lỗi nào? Bài 3: Một vận động viên tập ném bóng rổ, số lần bóng vào rổ của mỗi phút tập lần lượt là:
a) Dấu hiệu ở đây là gì? b) Lập bảng tần số và nhận xét. c) Tìm số bóng trung bình ném được vào rổ trong 1 phút. d) Tính mốt của dấu hiệu. e) Vẽ biểu đồ đoạn thẳng. Phương pháp giải: -Các số liệu thu thập được khi điều tra về một dấu hiệu gọi là số lệu thống kê. Mỗi số liệu là một giá trị của dấu hiệu. - Số tất cả các giá trị của dấu hiệu bằng số các đơn vị điều tra -Tần số của một giá trị: số lần xuất hiện của một giá trị trong dãy các giá trị của dấu hiệu gọi là tần số của giá trị đó. -Bảng tần số thường được lập như sau +Vẽ khung hình chữ nhật gồm 2 dòng +Dòng trên ghi các giá trị khác nhau của dấu hiệu theo thứ tự tăng dần +Dòng dưới ghi các tần số tương ứng với mỗi giá trị đó Ta cũng có thể lập bảng tần số theo hàng dọc Số trung bình cộng:__X=x1n1+x2n2+x3n3+...+xknkN x1,x2,...,xklà các giá trị khác nhau của dấu hiệu X n1,n2,...,nk là các tần số tương ứng X là số các giá trị -Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số, kí hiệu là Mo Biểu đồ đoạn thẳng: +Dựng hệ trục tọa độ, trục hoành biểu diễn các giá trị x, trục tung biểu diễn tần số n(độ dài đơn vị trên 2 trục có thể khác nhau) +Xác định các điểm có tọa độ là cặp số gồm giá trị và tần số của nó(giá trị viết trước, tần số viết sau) +Nối mỗi điểm đó với điểm trên trục hoành có cùng hoành độ LG bài 1 Phương pháp giải: Gọi sáu số lần lượt là a,b,c,d,e,f. Theo bài ra ta có a+b+c+d+e+f6=4 ⇒ a+b+c+d+e+f=24 (1). Thêm số thứ bảy vào ta có a+b+c+d+e+f+g7=5 ⇒ a+b+c+d+e+f+g=35 (2). Từ (1) và (2) ⇒ g=35−24=11. Vậy số thứ bảy là 11. LG bài 2 Lời giải chi tiết: a) Số lỗi trung bình của mỗi bài kiểm tra: ¯X=1.7+2.19+3.6+4.2+5.1+6.140=8240≈2,05. b) Mốt của dấu hiệu: M0=2. Đơn vị điều tra: các em học sinh. c) Có 40−36=4 bài viết không có lỗi nào. LG bài 3 Lời giải chi tiết: a) Dấu hiệu là: “Kỹ năng ném bóng rổ của một vận động viên”. b) Bảng tần số:
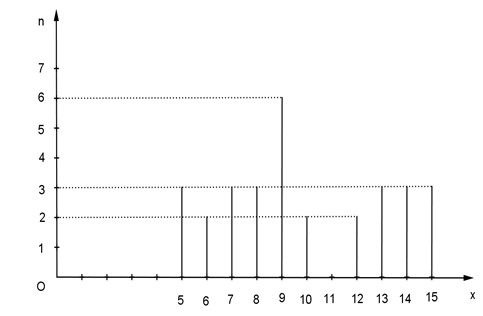
Số các giá trị của dấu hiệu: 30. Số các giá trị khác nhau: 10. Giá trị lớn nhất: 15. Giá trị nhỏ nhất: 5. Giá trị có tần số lớn nhất: 9. Giá trị có tần số nhỏ nhất: 6; 10;12. Các giá trị chủ yếu là: 8; 9. c) Số bóng trung bình được ném vào rổ trong 1 phút: ¯X=5.3+6.2+7.3+8.3+9.6+10.2+12.2+13.3+14.3+15.330=29630≈9,87. Mốt của dấu hiệu: M0=7. d) Mốt của dẫu hiệu: M0=9. e) Vẽ biểu đồ:
HocTot.Nam.Name.Vn
|