Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 2 - Hình học 7

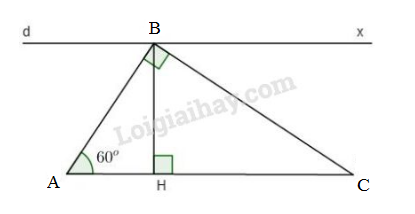
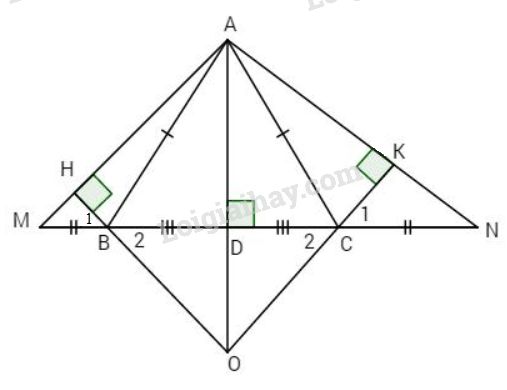
Đề bài

Bài 1: Cho tam giác ABC vuông tại B có $\widehat A = {60^o}$, kẻ BH vuông góc với AC (H thuộc AC). Qua B kẻ đường thẳng d song song với AC.

a) Tính góc $\widehat {ABH}$.

b) Chứng minh d vuông góc với BH.

c) Hãy so sánh góc $\widehat {ABH}$ và $\widehat {CBx}$ (theo hình vẽ).

Bài 2:  Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M. Trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh $\Delta AMN$ là tam giác cân.

b) Kẻ BH vuông góc với AM (H thuộc AM), CK vuông góc với AN (K thuộc AN). Chứng minh rằng BH = CK.

c) Gọi O là giao điểm của BH và CK. Chứng minh  $\Delta OBC$ cân.

d) Gọi D là trung điểm của BC. Chứng minh rằng A, D, O thẳng hàng.

LG bài 1

Phương pháp giải:

+$\left\{ {\begin{array}{*{20}{c}}{a \bot b}\\{b//c}\end{array}} \right. \Rightarrow a \bot c$

+Tổng hai góc nhọn trong tam giác vuông bằng 90 độ

Lời giải chi tiết:

a) Ta có $BH \bot AC$ (giả thiết) nên $\Delta BHA$ vuông tại H có $\widehat A = {60^o}$ (giả thiết)

$\Rightarrow \widehat {ABH} = {90^o} - {60^o} = {30^o}$.

b) $\left\{ \matrix{  d//AC\, (gt) \hfill \cr  BH \bot AC\,(gt) \hfill \cr}  \right. \Rightarrow d \bot BH.$

c) Ta có $\widehat {ABH} + \widehat {HBC} = \widehat {ABC} = {90^o}$(giả thiết)   (1)

Lại có $d \bot BH$ (chứng minh trên) $\Rightarrow \widehat {CBx} + \widehat {HBC} = {90^o}$ (2)

Từ (1) và (2) $\Rightarrow \widehat {CBx} = \widehat {ABH} = {30^o}$.

LG bài 2

Phương pháp giải:

Sử dụng:

Tổng hai góc kề bù bằng 180 độ

Hai góc đối đỉnh thì bằng nhau

Tia phân giác của 1 góc

Lời giải chi tiết:

a) Ta có  $\widehat {ABM} + \widehat {ABC} = {180^o}$ (kề bù).

$\Rightarrow \widehat {ABM} = \widehat {ACN}$.Tương tự $\widehat {ACN} + \widehat {ACB} = {180^o}$ mà $\widehat {ABC} = \widehat {ACB}$ (giả thiết).

Xét $\Delta ABM$ và $\Delta ACN$ có: AB = AC (giả thiết)

$\widehat {ABM} = \widehat {ACN}$ (chứng minh trên), BM = CN (giả thiết)

Do đó $\Delta ABM = \Delta ACN$(c.g.c) $\Rightarrow AM = AN$ (cạnh tương ứng)

Vậy $\Delta AMN$ cân tại A.

b) Ta có $\Delta BHM$ và $\Delta CKN$ vuông (giả thiết) có $\widehat {AMN} = \widehat {ANM}$ (chứng minh trên) và BM = CN (giả thiết).

Do đó $\Delta BHM = \Delta CKN$(g.c.g) $\Rightarrow BH = CK$ (cạnh tương ứng).

c) Ta có $\Delta BHM = \Delta CKN$ (chứng minh trên)

$\Rightarrow \widehat {{B_1}} = \widehat {{C_1}}$ (góc tương ứng) mà $\widehat {{B_1}} = \widehat {{B_2}}$(đối đỉnh).

Tương tự $\Rightarrow AO$ $\widehat {{C_1}} = \widehat {{C_2}}$ $\Rightarrow \widehat {{B_2}} = \widehat {{C_2}}$. Chứng tỏ $\Delta OBC$ cân.

d) D là trung điểm của BC (giả thiết) $\Rightarrow DB = DC$. Do đó $\Delta ADB = \Delta ADC$ (c.c.c) $\Rightarrow \widehat {DAB} = \widehat {DAC}$ hay AD là tia phân giác của góc $\widehat {BAC}$.

Chứng minh tương tự ta có $\Delta ABO = \Delta CAO$(c.c.c) $\Rightarrow AO$ là phân giác của góc $\widehat {BAC}$.

Vậy ba điểm A, D, O thẳng hàng.

HocTot.Nam.Name.Vn